基于数据挖掘的宽厚板板凸度控制

曹建国，江军，赵秋芳，何安瑞，李存福，孙旭东

(1.北京科技大学机械工程学院，北京，100083；2.北京科技大学国家板带生产先进装备工程技术研究中心，北京，100083；3.北京科技大学人工智能研究院，北京，100083；4.北华航天工业学院机电工程学院，河北廊坊，065000；5.江苏金恒信息科技有限公司，江苏南京，210045；6.南京钢铁股份有限公司，江苏南京，210035)

随着制造业对高强管线钢、压力容器板、船板等需求的提升，人们对宽厚板板形质量的要求日趋严苛，宽厚板轧机板形控制已成为宽厚板质量控制的关键技术之一。特别是对于火箭卫星外壳、船舰、海上平台、核能设备等钢板质量大的宽厚板产品，必须依靠5 m及以上强力宽厚板轧机才能轧制[1]，多为单机架多道次的可逆轧制过程，频繁的规格变化提升了宽厚板轧机板形控制的难度。宽厚板轧制过程中板形影响因素繁杂，因而难以进行机理建模，难以稳定实现宽厚板板凸度高精度有效控制。同时，由于缺乏适当的处理技术和方法，宽厚板生产过程积累的大量重要轧制过程数据未能得到充分的利用。数据挖掘作为20世纪末兴起的数据智能分析技术，能够从海量数据中自动分析潜在有用的知识，随着数据挖掘技术和数据挖掘产品的普及，各钢铁企业均开展了数据挖掘的研究，希望将数据挖掘应用于钢铁企业质量控制、质量改进等方面。国内外学者在中厚板轧制过程数值模拟[2−3]、板形控制策略[4−5]和数学模型[6−7]等方面取得了丰富成果。近年来，在宽厚板板形控制研究中也取得了积极进展：PRINZ等[8]针对宽厚板轧制过程中的横向不对称问题，提出一种基于宽厚板位置评估的前馈控制策略，在工业应用中有效提高了宽厚板平面形状的控制精度；穆志纯等[9]采用知识发现和数据挖掘的方法建立了一种将知识模型和数学模型相结合的轧制负荷分配模型，通过该模型生成的规程进行轧制可以提高宽厚板板形质量；李扬等[10]以带钢成品宽度质量分析为目标，利用关联规则挖掘得到带钢宽度质量缺陷与控制状态的对应关系，结合因子分析和故障逻辑分析方法进行带钢质量的综合评估。国内某宽厚板CVC plus 大型骨干轧机具有工作辊窜辊、工作辊弯辊和CVC plus 辊形等先进的板形控制手段，是世界上轧制扭矩最大和我国轧制压力最大的宽厚板轧机之一，实际生产中存在板凸度偏大且难以控制的问题。本文作者结合数据挖掘以及宽厚板生产特点，基于历史数据建立高精度的板凸度预测模型，在离散的状态空间上对基于主成分分析方法提取的关键控制变量与预测板凸度状态间进行关联规则挖掘，结合控制变量影响力评估实现不同板凸度质量状态下关键控制变量的快速定位以及对板凸度的有效控制，避免机理建模对问题分析带来的困难，实现对历史数据中蕴含信息的充分利用，为宽厚板板凸度控制研究提供参考。

1 现场数据采集与分析

国内某宽厚板CVC plus 大型骨干工业轧机采用单机架多道次的可逆轧制方式，能够进行最小厚度为8 mm、最大宽度为4 850 mm以及厚度超过100 mm的高品质宽厚板的轧制。现场测量210 块Q345 钢宽厚板板凸度，测量结果如图1所示。在实际生产过程中，宽厚板板凸度一般要求控制为0.12 mm 左右，0～0.15 mm 属于可接受范围，板凸度超过0.15 mm 时表示凸度控制应引起足够的重视，板凸度超过0.2 mm 时判定为不合格。在现场采集数据中，板凸度大于0.2 mm的宽厚板占比为6.2%，板凸度为0.15～0.20 mm的宽厚板占比为35.7%，其板凸度质量控制存在较大的提升空间。同时，由于其产品规格多，不同规格宽厚板的轧制工艺存在差异，包含有11道次、13道次、15道次和17道次等的可逆轧制过程，轧制过程工艺参数较为繁杂，为宽厚板板凸度质量控制研究带来了较大阻碍。

图1 Q345钢板板凸度分布Fig.1 Distribution of Q345 steel plate crown

2 宽厚板板凸度预测模型的建立

为及时采取有效措施避免板凸度质量问题的发生，宽厚板板凸度控制需要通过对历史生产数据分析以实现待轧制宽厚板板凸度质量的预先判定，因此有必要建立高精度的宽厚板板凸度预测模型进行研究。虽然神经网络等人工智能算法具有很强的非线性和自学习能力，但这类单分类器对训练样本的依赖程度过高并且容易出现过拟合的现象[11]，为提高板凸度预测的准确度和稳定性，采用随机森林集成方法建立板凸度预测模型。

2.1 选取预测因子

由于宽厚板轧制主要在精轧阶段进行板凸度控制，因此选取精轧10道次稳定轧制阶段的轧制过程数据建立预测数据集，并进行变量重命名以区分各道次轧制过程控制变量，如dthick_en_1代表第1道次轧件入口厚度。根据现场经验，选取包含各道次出口厚度、弯辊力和窜辊量等在内的83个控制变量作为备选解释变量。为减小解释变量维度过高对预测模型计算效率的影响，对解释变量作进一步筛选。依据均方误差对解释变量的重要性进行排序，随机改变解释变量取值并生成对应的随机森林模型，计算袋外数据(out of bag,OOB)误差，OOB 误差变化越大则解释变量的重要性越高[12]。同时，对数据集进行十折交叉验证(10-fold cross-validation)，得到OOB 误差随变量数的变化关系，如图2所示。由图2可以得出：当变量数为42个时，OOB 误差最小，因此，选取重要性排序在前42 位的变量作为随机森林预测模型的预测因子。

图2 OOB误差随变量数变化曲线Fig.2 OOB error curve with variable number

2.2 参数选择和优化

随机森林模型中需要设置随机森林决策树数ntree和决策树每个节点处随机选取的候选特征数mtry这2个主要参数，ntree一般不少于100棵，默认值为500 棵，mtry一般取为预测因子数的1/3[13]。为避免单纯依靠经验选取模型参数可能带来的预测偏差，采用遍历的方法确定随机森林模型参数ntree和mtry最佳值。分别计算ntree在和mtry所有取值情况下的袋外误差，袋外误差最小时的参数值就是ntree和mtry的最佳取值。将mtry的取值范围设定为12～18个，ntree可选择的取值设定为500，1 000，1 500和2 000 棵，袋外误差随mtry和ntree的变化如图3所示。由图3可知：mtry和ntree的最佳取值分别为16个和1 000个。

210组数据中随机选择170组数据组成训练集，其余40 组数据组成测试集，采用自助抽样法(bootstrap)随机产生1 500个子训练集并生成对应未剪枝的决策树。从43个特征中随机抽取16个特征作为节点的分裂特征集，在每个节点处以Gini 指数为标准从16个特征中选择最佳的分裂方式，分裂过程不进行剪枝使每棵决策树最大限度地生长。取1 000棵决策树输出结果的平均值作为最终的板凸度预测结果。随机森林预测模型计算流程如图4所示。

图3 袋外误差随mtry和ntree变化曲线Fig.3 OOB error variation curve with mtry and ntree

2.3 建立预测模型

应用经过训练的RF 模型进行测试集板凸度预测，预测结果如图5所示。依据预测结果分别计算模型平均相对误差绝对值MMRE、均方根误差RRMSE和确定性系数R2，分别统计训练阶段和测试阶段模型的性能指标，以对模型的可靠性和精度进行评价，结果如表1所示。由表1可知：RF模型精度较高，测试期预测相对误差未超过训练期预测相对误差，泛化性较好；均方根误差反映误差波动程度，RF 模型2个阶段预测均方根误差均较小，预测值比较稳定；确定性系数反映预测准确性，测试期与训练期的确定性系数均接近1，预测数据基本可以拟合实际数值，因此预测模型能合理准确地对板凸度进行预测。从图5 可以看出：RF 预测结果与实际值较为吻合。综上可知，RF 预测效果理想，表现出良好的泛化性能，能够满足宽厚板板凸度预测要求。

3 基于关联规则挖掘的宽厚板板凸度质量分析

关联规则挖掘是数据挖掘中的一种重要技术手段，对于由随机森林模型板凸度预测结果和对应轧制过程工艺参数的1 208 组数据构成的数据库，应用关联规则中的Apriori 经典算法分析找出板凸度与控制状态之间的强关联关系，得到轧制过程工艺参数对于板凸度的影响规律，有助于快速定位轧制过程中造成板凸度偏大的关键工艺参数。

3.1 主成分分析法数据降维

由于宽厚板多道次可逆轧制过程中影响板凸度的因素复杂多样，各因素相互作用共同决定了最终的板凸度，但各因素重要性存在一定差异，同时对板凸度的影响规律也不完全相同，在进行板凸度分析时要抓住关键过程控制变量，忽略次要因素对板凸度的影响。因此，在进行关联规则挖掘前有必要进行数据降维工作，同时对于减少冗余规则数具有重要作用。

图4 随机森林模型板凸度预测计算流程Fig.4 Calculation process of plate crown using random forest prediction model

图5 RF模型预测结果Fig.5 RF model prediction results

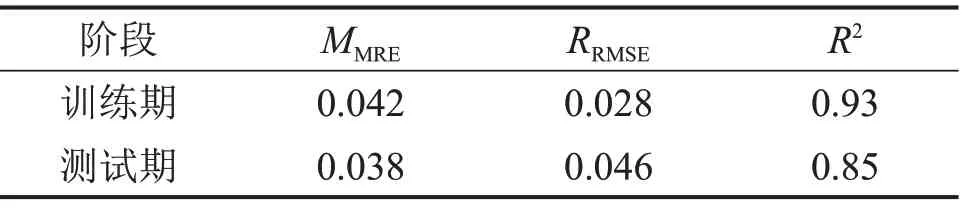
表1 训练期和测试期RF模型预测性能Table 1 Prediction performances of RF model in training and testing periods

主成分分析是最常用的线性降维方法，通过某种线性投影将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以使用较少的数据维度，同时能够将数据包含信息的损失降为最低[14]。

对于样本矩阵x：

式中：p=1,2,…,83;n=1,2,…,1 208。

对式(1)进行Z标准化处理，得到标准化后的向量x*为

计算x*协方差矩阵的特征值λ1,λ2,…,λp和特征向量ω1,ω2,…,ωp，则主成分的贡献率P表示为

提取特征值大于1的13个主成分，该13个主成分的累积贡献率为90.10%，可以用于代表全部数据信息。由于主成分因子没有明确的实际含义，不能作为实际的控制变量，但主成分中影响显著的变量可以代表主成分包含的主要信息，因此通过主成分载荷矩阵进行关键变量的选取[15]。主成分载荷矩阵反映主成分与原始变量间的相互关联程度，原始变量xj在第p个主成分zi上的载荷lij可以表示为

式中：i,j=1,2,…,83；λi为特征值，ωij为特征向量ωi的第j个分量。

选用每个主成分中影响最为显著的变量作为关键控制变量，以此来降低产生规则的规模，由于第一主成分包含的信息最多，因此，从第一主成分中选取3个关键控制变量。筛选出的关键控制变量如下：dthick_ex_1，dthick_ex_2，dthick_ex_3和dthick_ex_4分别为第1道次、第2道次、第3道次和第4道次出口厚度；Swr_shift_1，Swr_shift_6和Swr_shift_10分别为第1道次、第6道次和第10道次窜辊量；Ttemp_en_2，Ttemp_en_3和Ttemp_en_4分别为第2道次、第3道次和第4道次入口温度；Ttemp_ex_10为第10道次出口温度；Qwr_bend_5，Qwr_bend_6和Qwr_bend_9分别为第5道次、第6道次和第9道次弯辊量；froll_force_10为第10道次轧制力。

关键控制变量的影响力w指的是关键控制变量对于最终宽厚板板凸度的影响权重，在数值上等于控制变量对主成分因子具有最显著载荷l的绝对值与该主成分的贡献率P的乘积，具体计算公式为

式中：p=1,2,…,83;n=1,2,…,1 208。

下面进行关键控制变量影响力的计算，并将计算结果进行量纲一处理，按照从大到小的顺序进行排序，得到关键控制变量的权值向量表，如表2所示。

3.2 数值型属性的离散化

Apriori 算法要求数据集中的数据类型必须为离散型，在应用Apriori 算法进行关联规则挖掘前需进行数据的离散化操作[16]。进行目标变量(关联规则后件)离散化操作时，根据实际生产经验可知：宽厚板板凸度一般会控制为0.15 mm左右，板凸度超过0.2 mm时判定为不合格。根据这一实际情况，本文将板凸度划分为A1，B1和C1这3个等级，如表3所示。通过目标变量的离散化操作赋予数据集类信息。

表2 关键控制变量权值Table 2 Weight of key control variables

表3 板凸度离散化结果Table 3 Discrete results of plate crown

采用聚类分析进行关联规则前件即控制变量数值型属性的离散化，聚类分析考虑属性的取值分布和数据点的相邻性，可以得到较理想的数据离散化结果[17]。采用Matlab编程实现K−means聚类算法进行数据离散化操作，将每个属性划分为8个区间(簇)，随机选出8个数据项作为各簇的初始中心，分别计算剩余的数据项与各个簇中心的距离，将其归入距离最短的簇中并重新计算8个簇的中心。重复进行上述过程，直至平方误差准则函数E收敛。

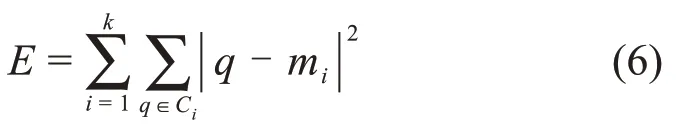
式中：E为数据集中所有数据项的平方误差和；q为数据项；mi为簇Ci的均值；k为簇的数目。

为使数据规整以便于进行数据挖掘，进一步将离散区间映射成连续的字母标识，如Swr_shift_1的离散化结果如表4所示。

3.3 基于Apriori算法的关联规则挖掘

设项集Xt={i1,i2,…,ip}(p=1,2,…,15)，Y={b}，其中i1,i2,…,ip分别代表dthick_ex_3，dthick_ex_4，dthick_ex_1等15个关键控制变量1个值域内的子区间，b代表板凸度取值的1个子区间，包含A1，B1和C1这3个等级，需要寻找出形如X⇒Y的关联规则[18]。由于宽厚板凸度为B1和C1等级出现次数较少，这些少数状态是进行板凸度分析需要重点研究的内容，因此，在进行关联规则分析时需设置1个较低的支持度，设定最小支持度为1%，最小置信度为50%。由于板凸度为A1的控制状态出现次数最多，在产生对应的关联规则时将最小置信度设置为80%以保证关联规则的有效性。筛选目标厚度为20 mm 且目标宽度为3 910 mm、目标厚度为25 mm 且目标宽度为3 150 mm和目标厚度为35.5 mm且目标宽度为4 240 mm这3种典型规格样本的关联规则，如表5所示。

4 基于关联规则的关键工艺参数调整策略及仿真分析

4.1 基于关联规则的关键工艺参数调整策略

在数据挖掘数据集中查找满足板凸度等级为A1时对应关联规则的样本，从中选取宽厚板凸度最小的样本组成标准样本集，作为关键工艺参数调整的参照标准，如表6所示。当来料情况一定时，规格相同的宽厚板轧制过程各板形调控手段的使用会发生变化，现场技术人员会根据实际轧制条件做出调整，最终宽厚板板凸度也会存在差异。将板凸度等级为B1和C1与板凸度等级为A1对应的关联规则中存在的相同控制变量作为需要调整的关键控制变量，将关键控制变量的差异性作为制定调控策略的依据，并参照标准样本集关键控制变量设定值进行相应调整，以实现对板凸度的控制。通过适当调整关键控制变量实现良好的板凸度控制，并以典型厚度规格样本与所选取标准样本关联规则对比分析结果为依据，制定关键工艺参数调整策略。

表4 Swr_shift_1离散化结果Table 4 Discrete results of Swr_shift_1

表5 3种典型规格下样本的关联规则Table 5 Association rules of samples with three typical specifications

表6 标准样本集Table 6 Standard sample set

所建立的关键工艺参数调整策略如下：

1)在进行目标厚度为20 mm、目标宽度为3 910 mm的宽厚板轧制时，在现阶段轧制工艺条件下，应减小精轧第5道次的弯辊力，将其保持在1 914～2 137 kN，应在第6道次进行正窜辊，窜辊量设定为50.5～69.7 mm，此时精轧第6道次的辊缝由负凸度变为正凸度，减小了第6道次的板凸度。

2)在进行目标厚度为25 mm、目标宽度为3 150 mm的宽厚板轧制时，在现阶段轧制工艺条件下，应减小精轧第6道次和第10道次的窜辊量，将第6道次的窜辊量控制为8～29 mm，第10道次的窜辊量控制为6.6～30.7 mm。

3)在进行目标厚度为35.5 mm、目标宽度为4 240 mm的宽厚板轧制时，在现阶段轧制工艺条件下，应减小精轧第5道次的弯辊力，将其控制为2 817～3 108 kN，同时减小精轧第10道次的负窜辊量，将其控制在−55.7～−33.8 mm，在精轧最后一个道次通过CVC plus 轧机的工作辊负窜辊进一步减小宽厚板的板凸度。

4.2 基于关联规则的关键工艺参数调整策略有限元分析

运用大型通用商用有限元软件ANSYS 建立宽厚板辊件一体化三维弹塑性有限元耦合分析模型[19−21]，通过辊系弹性变形模型获取有载辊缝形状并加载到轧件弹塑性变形模型中进行宽厚板关键工艺参数调整策略的仿真计算，用于验证方法的可行性。在建立辊系弹性变形模型时，由于轧辊辊身的对称性以及上、下轧辊的反对称性并考虑计算资源的限制，建立辊系的1/4模型，对工作辊与支持辊辊间接触区域以及工作辊与轧件间接触区域选用Solid95 二十节点六面体高阶等参单元，其余部分选用Solid45 八节点六面体等参单元。在工作辊和支持辊以及工作辊与轧件之间可能发生接触的区域附加接触单元，对于工作辊和支持辊间的面−面接触，将支持辊表面设置为目标面，工作辊表面设置为接触面；对于工作辊和轧件间的面−面接触，将工作辊表面设置为目标面，轧件表面设置为接触面，目标面使用的单元号为Target170，接触面使用的单元号为Contact173[19]。在建立轧件弹塑性变形模型时，取辊系和轧件的1/4 进行建模，轧辊采用刚性材料模型，轧件采用双线性等向强化弹塑性材料模型，采用Solid164六面体实体单元划分网格[20]，辊系采用间接耦合。建立的有限元耦合模型中轧辊的综合辊形包含原始磨削辊形、磨损辊形和热辊形。建模参数如表7所示，建立的有限元模型如图6所示，其中轧件模型厚度方向网格划分为10层。

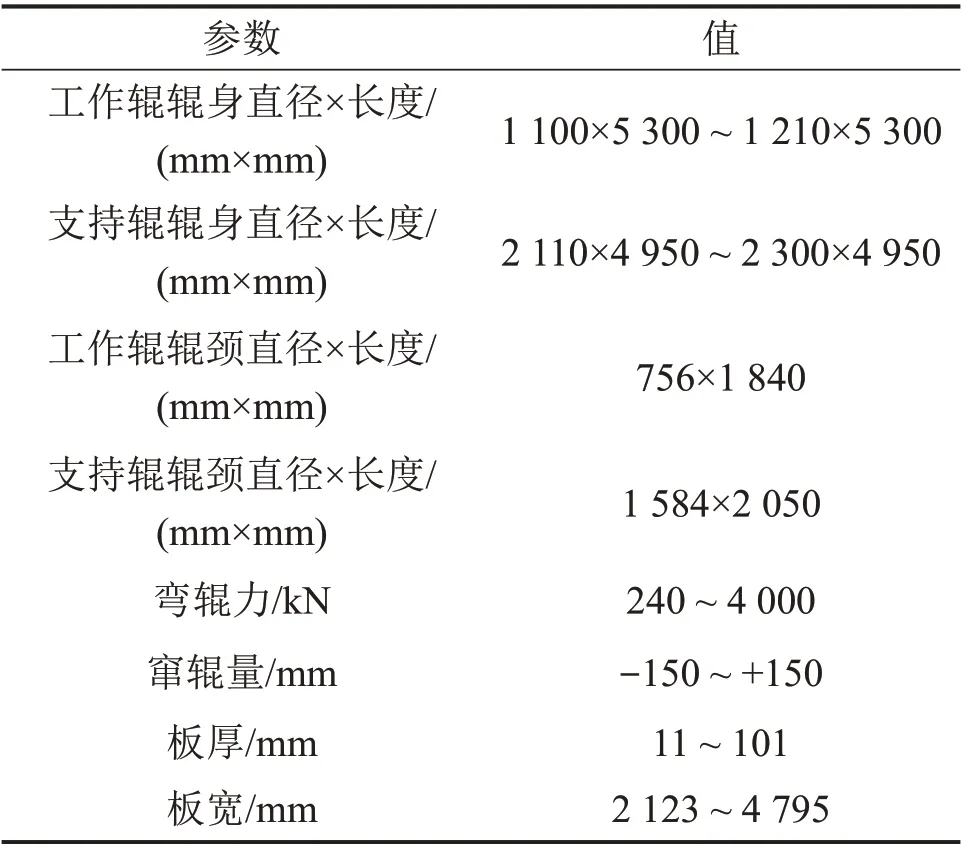
表7 有限元模型建模参数Table 7 Parameters of finite element model

选取精轧阶段轧制工艺参数对应的3个工况进行初始条件设置，如表8所示。精轧板入口厚度分别为112.961，145.240和137.420 mm，板宽度分别为4 640.53，3 934.74和3 763.26 mm。依据有限元分析结果计算得到的板凸度分别为0.175，0.130和0.156 mm，实际测得的板凸度分别为0.163，0.120和0.148 mm，相对误差为7.4%，8.3%和5.4%，有限元模型计算精度满足工程要求。

图6 三维弹塑性有限元耦合模型Fig.6 Three-dimensional elasto-plastic coupled finite element model

表8 仿真工况Table 8 Simulation conditions

分别选取编号为1810263705，1810195834和1810263208的样本作为测试样本，应用有限元耦合模型进行精轧10道次轧制过程的仿真计算，各个样本的板凸度预测结果以及仿真计算结果如表9所示。由表9 可以看出：3个测试样本的板凸度都在0.15 mm以内，板凸度得到了良好控制，说明本文提出的关键工艺参数调整策略对于进行板凸度控制是有效的，可为开展板凸度控制工业实验提供参考。

表9 板凸度仿真计算结果Table 9 Simulation results of plate crown

5 结论

1)应用随机森林集成方法建立了宽厚板板凸度预测模型，模型预测结果的平均相对误差绝对值、均方根误差和确定性系数分别为0.038，0.046和0.850，表现出良好的泛化性能，能够实现高精度的宽厚板板凸度预测。

2)通过主成分分析方法将数据集由83 维降至15 维，采用聚类分析方法进行数值型属性的离散化操作，通过关联规则挖掘实现对不同板凸度控制状态下轧制过程关键控制变量的快速定位，并应用于3 种典型规格宽厚板关键工艺参数调控策略。

3)建立了三维弹塑性有限元耦合模型，对3种典型规格工艺参数调控策略进行了仿真分析，板凸度分别下降了30.9%，14.7%和23.9%，说明基于关联规则的关键工艺参数调整策略可较好地控制板凸度，为开展基于数据挖掘的板凸度控制工业实验提供了参考依据。