基于相似性分析的工序质量控制研究及应用

周康渠，游思琦，杨 坤

(重庆理工大学 机械工程学院， 重庆 400054)

随着经济和技术的发展，制造业的生产模式已逐渐由大批量生产转为多品种小批量生产。大批量生产主要是利用统计过程控制SPC(statistical process control)对生产过程进行监控，确保生产加工的质量。但SPC应用需要大量的质量样本数据作为基础，而多品种小批量生产的质量样本数据又常常不能满足要求，因此研究基于SPC的多品种小批量生产质量控制方法具有重要的现实意义。国内外相关学者对多品种小批量生产质量控制问题展开了研究。史秀珍[1]对多品种小批量的加工特点进行了分析，探讨了统计质量控制的应用手段和理论方法。针对多品种小批量加工过程中样本数量不足的难题，王丽颖等[2]提出了虚拟工序概念，通过建立工序质量特征编码系统，将编码相同的工序划分为一个虚拟工序组，构成虚拟的样本批量。李迎吉等[3]提出基于成组技术的控制图理论，将相似工序归类成组并应用在制造过程质量系统中。针对控制图的相关问题，郑辉等[4]在常规控制图基础上选择控制性能更加灵敏的多元动态质量控制图，建立常见的多元动态控制图性能对比分析模型，并提出相应的选择策略。Ming等[5]发展了多元动态质量控制理论，提出基于Hotelling t2控制图的优化设计方案和可变抽样区间的控制方法。Celano等[6]考虑到小批量生产过程的有限抽样数量，研究了t控制图的监控性能及其统计属性。Castagliola等[7]研究了样本数据未知情形下EWMA控制图的设计方法，对比了CUSUM控制图和EWMA控制图的不同检出效果，总结了2种控制图的适用场合。

众多研究和实践表明，对大批量生产过程的质量控制问题，SPC已经形成较为完善的方法和技术体系。但在现有研究中，由于样本数量不足，将SPC应用到多品种小批量生产的研究还很薄弱。张根保等[8]用相似元理论对多品种小批量生产的工序能力进行分析,视多品种小批量生产的相似工序为大批量生产的相同工序，给出了用SPC来解决多品种小批量生产质量控制问题的思路。本文利用相似性原理对多品种小批量生产的不同零件的工序进行相似性判定，采集具有相似性工序的零件质量数据作为样本，通过数据转换，扩大样本数据量，克服多品种小批量生产质量样本数据不足的问题，实现利用SPC对多品种小批量生产进行质量控制。

1 工序的相似性分析与判定

1.1 工序质量影响因素分析

工序质量控制是利用控制图的判断准则监控生产过程是否处于稳定状态，如果不稳定则及时采取有效措施进行改善[9]。根据基础工业工程及质量控制相关理论，工序质量的主要影响因素可归纳为：操作人员、设备、材料、加工方法、环境和测量6个方面(简称5M1E，即工序质量的一级影响因素)，每个方面又可分解为不同的影响因素(即工序质量的二级影响因素)。在机械加工中，判定不同加工工序的相似性主要是通过对5M1E进行分析。以加工轴类零件工序为例，工序质量影响因素分析如表1所示。

表1 轴类零件工序质量影响因素

1级影响因素2级影响因素2级影响因素特征操作人员职业资格等级初级、中级、高级作业绩效差、中、良、优设备机床类型车床、铣床、钻床等加工刀具外圆车刀、端面车刀、螺纹车刀、铣刀等机床夹具通用夹具、专用夹具等材料毛坯材质45#钢、合金钢、铸铁等毛坯形状圆柱体零件加工尺寸直径、长度加工方法热处理方法正火、退火、淬火等加工类型车、钻、铣等加工精度等级IT1-IT18环境工作环境温度低、适中、较高、高照明强度弱、适中、较强、强振动弱、适中、较强、强噪声弱、适中、较强、强测量测量等级证书初级、中级、高级测量仪器游标卡尺、外径千分尺测量系统分析值GRRGRR所占百分比

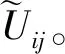
1.2 工序相似度计算

通过计算多品种小批量生产中不同零件工序的5M1E的相似度Q来判定工序的相似性[10]。工序相似度Q计算步骤如下：

1) 确定各级影响因素的权重。采用层次分析法AHP(analytic hierarchy process)来确定各级影响因素的权重[11-15]。设1级影响因素的权重集为D={D1,D2,…,Di}；2级影响因素的权重集为d={d11,d12,…,dij}。

(1)

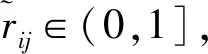
(2)

4)工序相似度计算。将1级影响因素的相似度Ri与1级影响因素的权重Di加权求和可得工序相似度Q为:

(3)

当两工序的相似度Q≥0.9时，则可判定为两工序是相似的[17]。

2 数据转换与质量控制图

2.1 基于相对公差法的数据转换

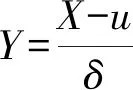
相对公差法的转换准则为：转换值=(实际测量值-测量均值)/公差带，即：

(4)

式中，样本数据采集对象为第g种零件中的第h个零件(g=1,2,3,…;h=1,2,3,…)。其中Tg为零件公差带。

本文采用实时均值法计算实时均值ugh为[19]：

(5)

由式(4)和 (5)联立求解可得实时样本数据的转换值Ygh。

(6)

(7)

式中Mg为零件的尺寸规格中心值。第g种零件中的第h个零件的移动极差Rs为

Rs=Ygh-Yg(h-1)

(8)

2.2 质量控制图的控制线参数确定

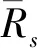
3 实例分析

3.1 轴类零件的车削工序相似性判定

以重庆空气压缩机厂曲轴加工工序为例进行分析。空气压缩机连杆处的曲轴，结构复杂，生产批量小，品种更换频繁，其性能直接影响到空压机的质量和寿命。在某一批次生产中，由同一操作人员在相同车床上精车5种不同规格的曲轴外圆。为保证测量的准确性，由2个同等级测量人员用相同游标卡尺进行测量，取其均值作为测量值。零件(A*-E*)分别对应加工工序(A-E)。毛坯材料均采用45#钢，加工零件的尺寸规格如表2所示。

表2 5种加工零件的尺寸规格

mm

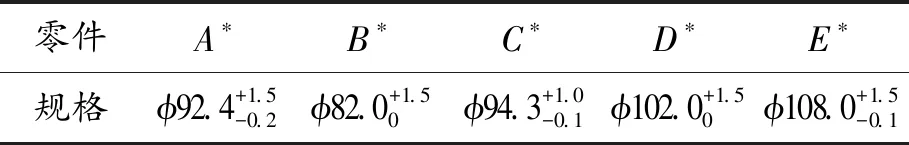
零件A∗B∗C∗D∗E∗规格ϕ92.4+1.5-0.2ϕ82.0+1.50ϕ94.3+1.0-0.1ϕ102.0+1.50ϕ108.0+1.5-0.1

利用相似性原理对不同加工工序进行相似性判定(因A*零件已有历史加工数据，故以A为目标工序，其他工序与目标工序进行相似性比较)，计算5种轴类零件的工序相似度Q。

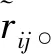
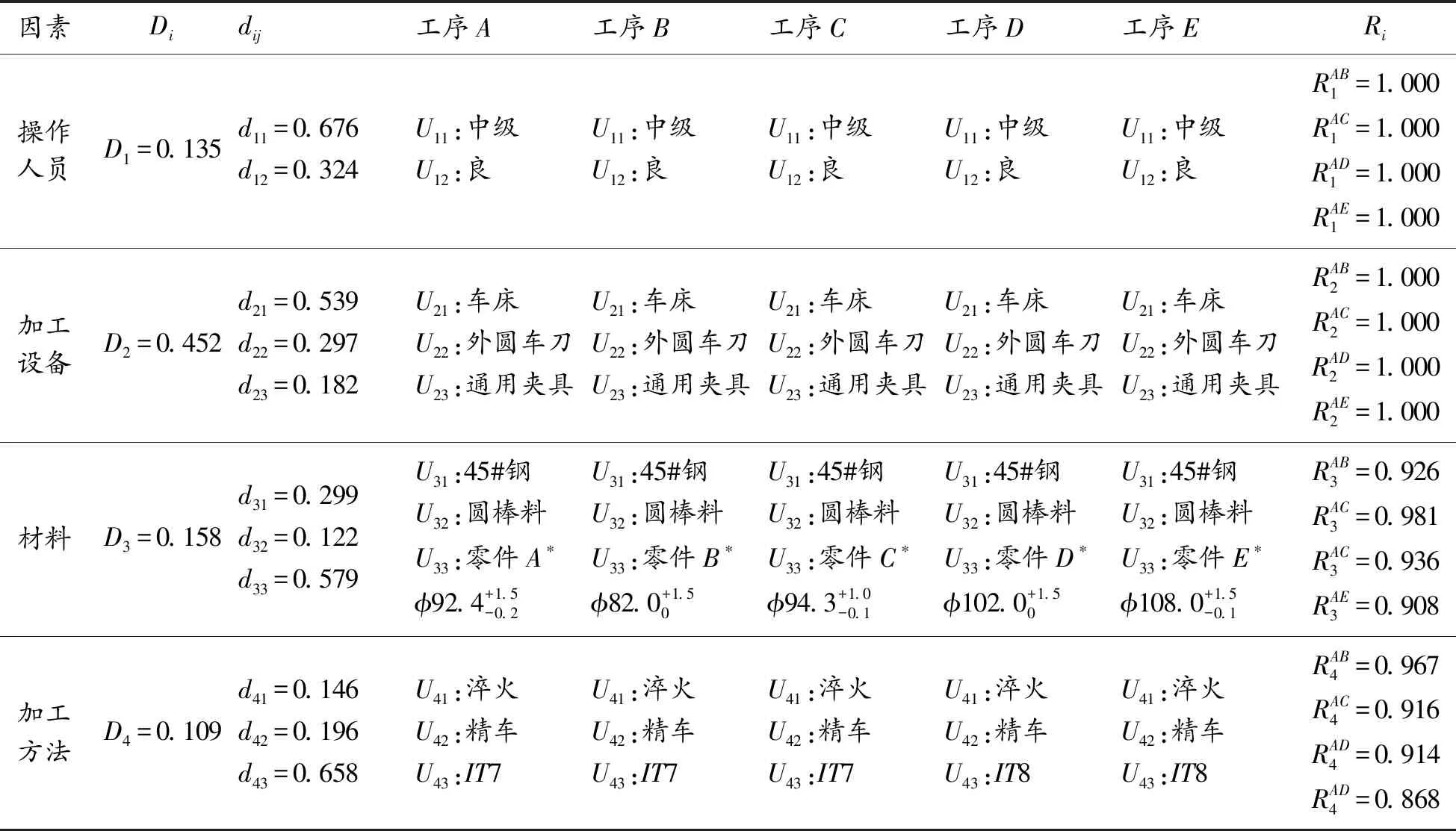
表3 5种加工零件的工序相似度

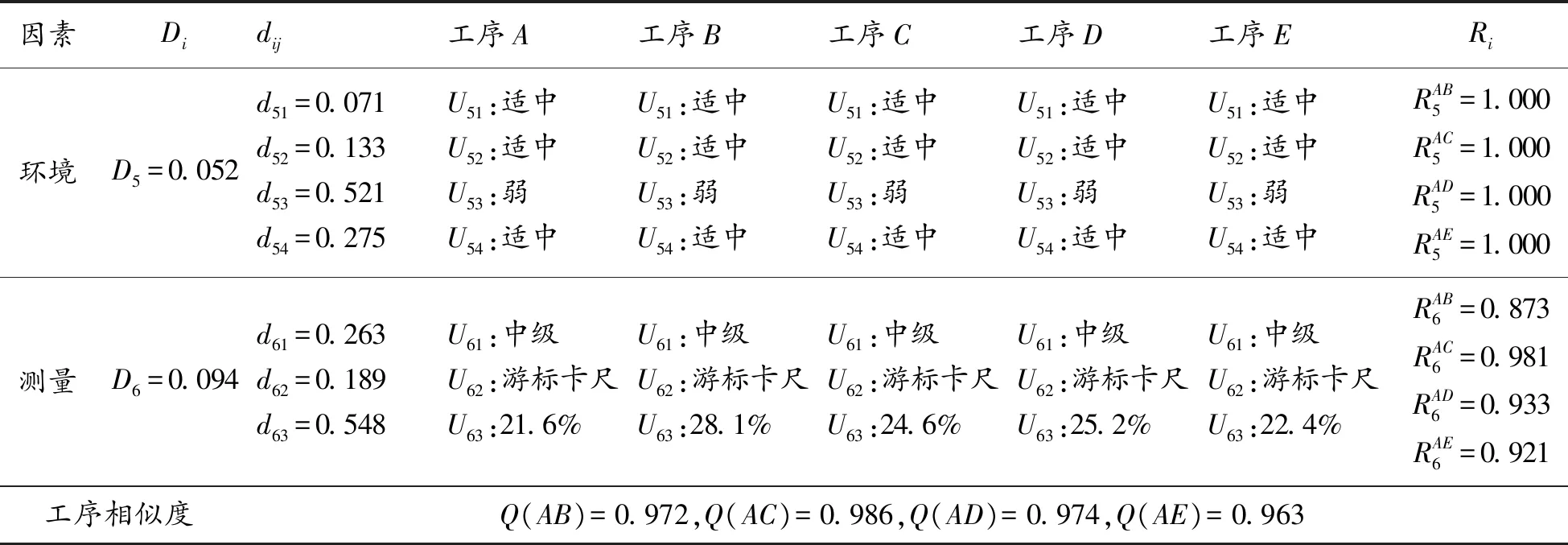
续表(表3)

3.2 车削样本数据的转换

因为A*零件的样本数据为历史加工数据，故采用式(4)进行数据转换，B*、C*、D*、E*零件为实时的加工数据，故采用式(5)～(7)进行数据转换，加工数据转换后的移动极差值均采用式(8)计算。采集的样本数据和转换的计算结果见表4。

表4 5种加工零件样本数据及转换值

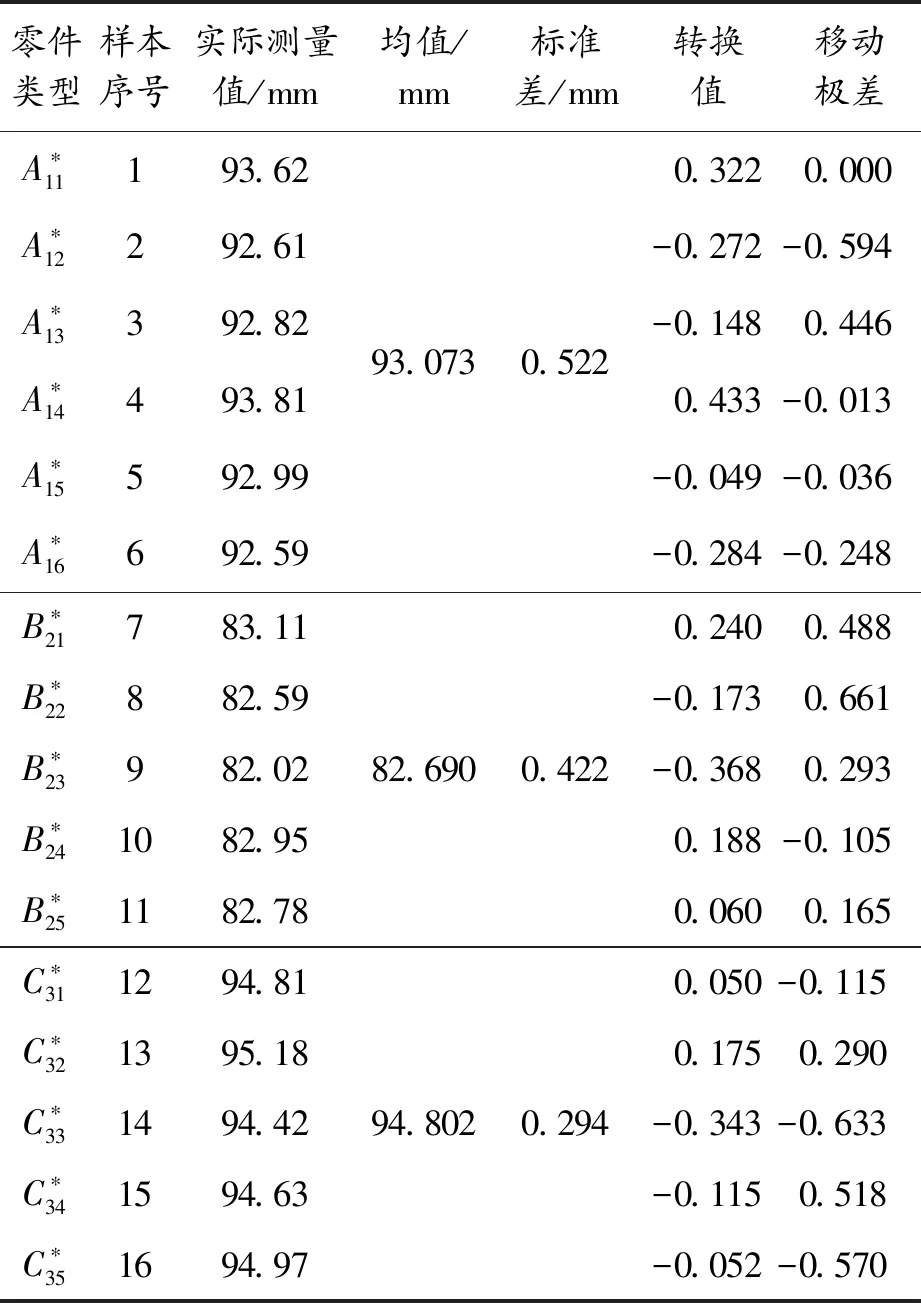
零件类型样本序号实际测量值/mm 均值/mm标准差/mm转换值移动极差A∗11193.62A∗12292.61A∗13392.82A∗14493.81A∗15592.99A∗16692.5993.0730.5220.3220.000-0.272-0.594-0.1480.4460.433-0.013-0.049-0.036-0.284-0.248B∗21783.11B∗22882.59B∗23982.02B∗241082.95B∗251182.7882.6900.4220.2400.488-0.1730.661-0.3680.2930.188-0.1050.0600.165C∗311294.81C∗321395.18C∗331494.42C∗341594.63C∗351694.9794.8020.2940.050-0.1150.1750.290-0.343-0.633-0.1150.518-0.052-0.570

续表(表4)

3.3 转换数据的正态检验

转换数据的正态检验可通过Minitab软件进行，检验结果如图1所示。根据P值大小判断转换数据是否服从正态分布,如果P>0.05即服从正态分布，反之则认为不服从[21]。图1中P=0.514>0.05，故转换后的数据服从正态分布。

3.4 转换数据的显著性检验

图2、3为多样本方差检验和单因子方差分析情况。根据P值大小判断转换值是否具有显著性差异。由图2可知，通过Bartlett检验,P=0.869>0.1,通过Levene检验,P=0.773>0.1,表明转换后的工序样本数据方差没有显著性差异(P≤0.1，转换数据具有显著性差异)[16]。同理，由图3可知，P=0.887>0.1，表明转换后的工序样本数据均值相对于公差中心偏移程度无显著性差异。因此，转换后的样本数据有统计意义，可以应用SPC对这5种零件精车外圆工序进行质量控制。

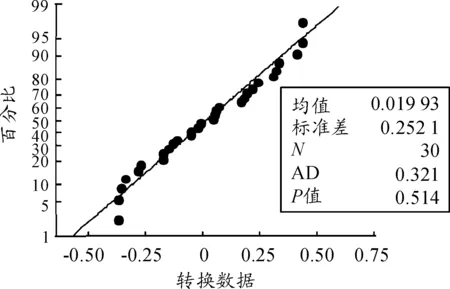
图1 正态检验

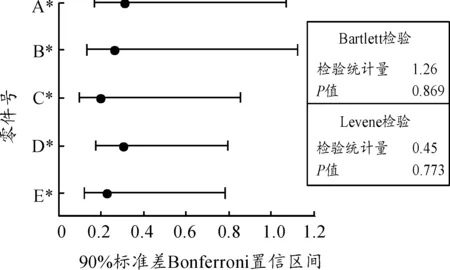
图2 多样本方差检验

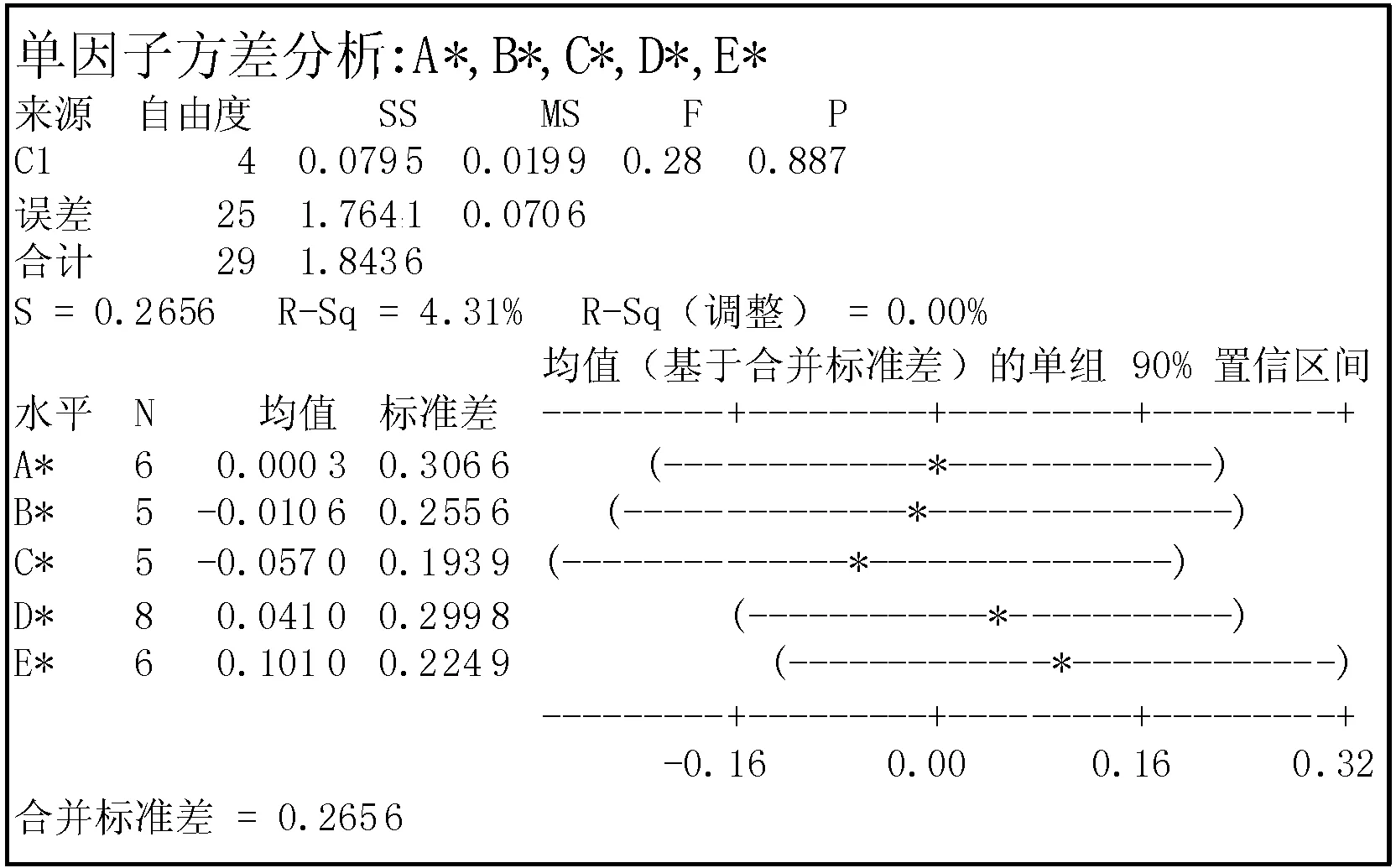
图3 单因子方差分析

3.5 建立质量控制图

根据本文2.2节质量控制图的控制线参数确定方法，将转换后服从正态分布且无显著性差异的样本数据代入控制线参数计算，绘制控制图如图4所示。对建立的质量控制图进行分析，依据控制图的判断准则以及图4可知，5种工序的数据转换值均落在控制线内并随机分布在中心线的两侧，表明5种曲轴零件精车外圆工序质量稳定，与实际生产情况相符。因此，当前生产过程处于稳定受控状态。

图4 单值-移动极差控制图

4 结束语

针对当前多品种小批量生产中十分棘手的质量控制问题，探讨了将SPC应用于多品种小批量生产的质量控制方法。首先，根据相似性原理分析多品种小批量生产工序的相似性，给出了工序相似度Q的计算过程，由相似度Q的大小判定多品种小批量生产的工序是否相似，将多品种小批量生产过程质量控制问题转换为大批量生产过程质量控制问题进行研究。其次，采集相似工序的零件加工数据作为样本，通过数据转换解决了多品种小批量生产中样本数据不足的问题。最后，对转换后的数据进行正态分布、一致性等检验，建立多品种小批量生产的质量控制图。实例表明，本文研究的多品种小批量生产工序质量控制方法可行，能够实现多品种小批量生产过程的质量控制，对提高相关企业的产品质量和竞争力具有重要作用。