基于轨道约束H∞滤波的北斗辅助列车定位算法研究

王鹏飞，李卫东，初宪武



基于轨道约束H∞滤波的北斗辅助列车定位算法研究

王鹏飞1, 2，李卫东1, 3，初宪武3

(1. 大连交通大学 机械工程学院，辽宁 大连 116028； 2. 河南工学院机械工程系，河南 新乡 453003； 3. 大连交通大学 电气信息工程学院，辽宁 大连 116028)

针对列车定位的高安全性和稳定性要求，结合列车行驶的特殊性，提出采用铁路轨道信息对北斗定位数据进行约束的H∞滤波算法。以模糊自适应“当前”统计模型为基础建立列车运动模型，通过将轨道近似为直线段，建立轨道约束模型。将轨道约束与H∞滤波器结合实现轨道约束H∞滤波算法。通过仿真对比分析H∞滤波与卡尔曼滤波、约束与无约束估计的误差。仿真结果表明：轨道约束在提高算法定位精度方面效果明显，H∞滤波在列车位置估计上具有鲁棒性优势。验证了轨道约束H∞滤波算法的有效性，对北斗辅助列车定位的工程应用具有理论指导意义。

轨道约束；H∞滤波；北斗卫星导航系统；列车定位

铁路运输具有单位能耗低、单次运量大、环境适应性强等特点，特别适合运输重载货物，其中部分高附加值货物关系到国家政治、军事以及民生等广泛利益。无论人员运输还是货物运输，提高铁路系统运输安全以及对铁路运输进行有效管理成为我国经济和社会发展中日趋紧迫的任务。欧美国家一直在用卫星定位跟踪技术为铁路运输提供有力的安全运行保障[1−2]。对于现代铁路运输系统来说，列车的跟踪与定位是其运行基础。随着科技进步，对列车的定位与控制要求越来越高，而全球导航卫星系统(Global Navigation Satellite System，GNSS)在其中具有重要的应用价值。以GPS为代表的GNSS系统在列车运行的定位解算、信息融合和安全评估等方面的应用发展迅速，欧美国家在此方面已有多年技术积累[3]，从目前铁路系统对于列车定位的需求来看，基于GNSS的列车定位系统的研究具有较大发展空间[4]。实践表明，利用国外卫星导航系统资源具有很大的风险性，不能满足我国对交通安全的要求。我国自主研发的北斗卫星导航系统(Beidou Navigation Satellite System，BDS)可军民两用，是国家安全保障的技术支撑系统[5]，对铁路相关应用具有重要的发展与应用潜力。经过多年发展，BDS已经能够为我国铁路和公路等交通领域以及经济和社会发展的各领域提供自主安全、高质量的卫星定位服务。尤其是近两年来，随着北斗3代系统的发射与组网以及北斗地基增强系统的快速建设，逐步可以为全球用户提供更优质的定位、导航和授时等服务。BDS作为一种全球卫星导航系统可以全天候、连续地对列车进行定位，具有实时定位精度高、成本低、维护方便等优势。同时，准确的位置信息对列车安全可靠地运行也至关重要，铁路运输及调度需要更为优化的列车定位技术[6]。因此，对基于BDS的列车定位方法进行深入研究，对于推动我国铁路运输业的发展具有重要意义。

1 北斗辅助列车定位

目前，列车一般常用的定位方法是轨道电路定位和应答查询定位。轨道电路定位法虽然简单有效，但是定位精度常会受到恶劣的气候和工作环境的影响。同时随着轨道电路放置的间隔不同，定位精度也有不同，其他的影响因素还有道砟阻抗和牵引电流等。应答查询定位可实现高精度定位，但是只能进行定点跟踪定位，需要沿途铺设应答器设备。测速定位是一种通过测量运行速度并根据时间推算距离，从而计算出列车位置的定位方法，但是也存在定位误差积分影响。因此，常规的列车跟踪定位方法无法实现对列车实时高精度跟踪定位。

BDS为列车安全运行提供了更多的定位信息与安全保障。但由于卫星信号的强度容易受到周围环境因素的影响，包括面临卫星星座、信号衰减与遮蔽、环境电磁干扰以及多径效应等多种因素，所以将BDS用于列车定位时还需要寻求方法弥补其缺陷，以保证列车可以进行连续准确可靠地定位，这也是北斗辅助列车定位的基础和前提[7]。

由于卫星易受外界环境影响，为了保证在卫星定位失效的情况下定位数据的持续输出，可以采用与惯性导航系统信息融合的方法进行辅助定位。这种方法具有容错能力强的优势。列车受各种影响因素，其运动具有不确定性，无法认为是单一的匀速、匀加速和匀减速运动，而且列车对定位的安全性和稳定性具有较高要求，所以鲁棒性算法更具有实际应用意义。

卡尔曼滤波是GNSS/INS组合导航的主要算法之一，其设计思路是出于最小线性方差估计[8]。其限制条件之一是要求首先确定系统噪声协方差矩阵和量测噪声协方差矩阵，而由于误差模型与真实系统的差异，阵和阵具有一定的不确定性。H∞滤波算法具有很好的鲁棒性，是针对阵、阵和估计误差协方差阵未知的算法[9]。其设计思路来自博弈论，需要预先设置代价函数，再做极小值或者设置H∞范数上界的求解。

H∞滤波的鲁棒性体现在对于未知统计特性的有界噪声均可以有效处理，而卡尔曼滤波的建模以零均值的随机过程为噪声。同时H∞滤波器以传递函数的范数最小或者小于预设值为目标。所以，相比卡尔曼滤波器，H∞滤波器具有强鲁棒性[10−11]。

H∞滤波能够有效抑制非高斯统计特性噪声的能力，结合轨道信息后，可以更好地实现对列车的定位与追踪[12]。所以，为了满足列车定位实时性和鲁棒性的要求，采用H∞滤波算法融合BDS定位信息与轨道约束信息，对列车进行定位解算。将轨道信息作为约束条件引入滤波方程，其思路是在原有滤波的基础上，利用轨道信息约束条件，对滤波方程中一步预测值的表达式作补充，即对一步预测值作修正，以改善滤波结果[13]。

2 列车运动模型

列车运动模型的准确性对滤波估计算法具有重要影响。为了能够真实地反映列车的运动，本文采用“当前”统计模型作为列车的运动模型，该模型具有加速度均值和方差的自适应性。

2.1 “当前”统计模型

实际列车的运动往往并不完全属于匀速或匀加速范围的运动。“当前”统计模型采用修正的瑞利分布来描述加速度的概率密度，认为当前加速度均值等于加速度预测值[14]。所以，当列车以某一加速度运动时，下一时刻的加速度取值是有限的，且只能在“当前”加速度的邻域内。

“当前”模型假定目标的加速度连续变化，加速度均值与当前时刻的加速度估计相等，方差由均值决定。该模型本质上是非零均值时间相关模型，其机动加速度的“当前”概率密度可用某种适当函数分布描述。

模型在估计目标状态的同时辨识加速度均值的取值范围，实时修正加速度的分布，最后以方差的形式反馈到下一时刻的系统滤波增益中，从而实现均值和方差的自适应滤波。

其一阶时间相关模型为：

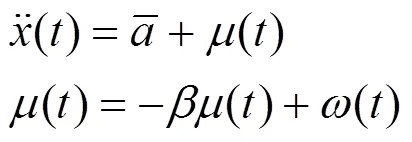
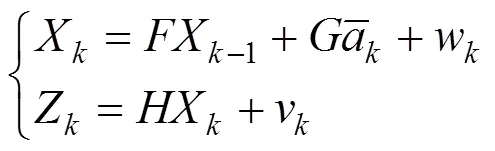
式中：

系统噪声协方差为：

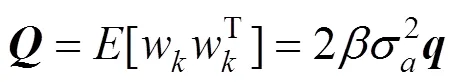
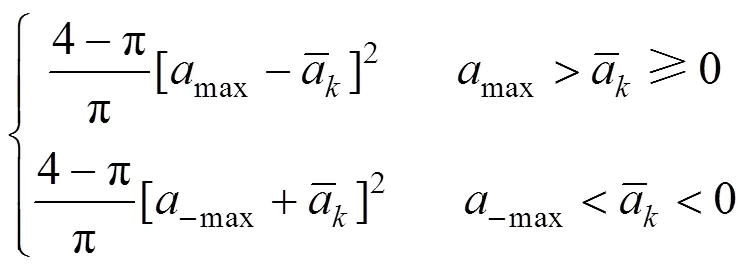
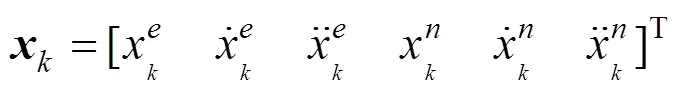
列车运动模型与式(2)表达相同，式中的，和做相应的调整。

2.2 模糊自适应调整

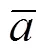
通过采用模糊自适应方法对加速度极限值进行自适应调整，可以加强当加速度均值较小时“当前”模型对目标的跟踪性能[16]。

引入模糊隶属度函数：

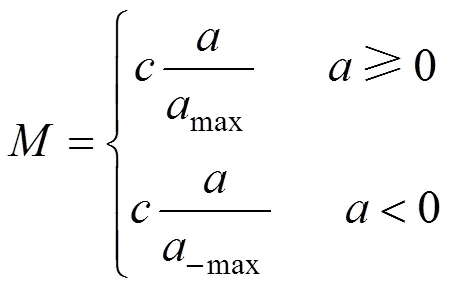
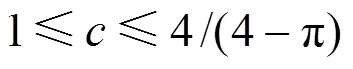
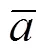
3 轨道约束H∞滤波算法

H∞滤波与卡尔曼滤波在应用场景和滤波目标方面具有一定的差异。H∞滤波是在系统具有模型不确定性时求最小化最大误差估计，而卡尔曼滤波是在系统模型和噪声等已知的前提下求最小均方误差估计。所以，H∞滤波相对卡尔曼滤波具有更好的鲁棒性，可将H∞滤波视为一个鲁棒形式的卡尔曼滤波[17]，而对于线性系统，状态等式约束估计优于无约束估计[18]。

3.1 传统无约束H∞滤波

H∞滤波可以稳定地处理未知统计特性的噪声，其计算过程与卡尔曼滤波类似。Ｈ∞滤波形式有多种，以文献[9]中的离散型Ｈ∞滤波为研究对象。

系统状态方程与量测方程为：

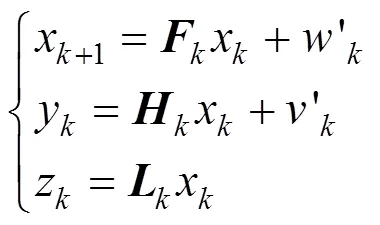
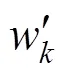
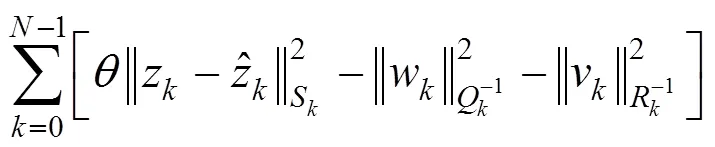
求解步骤为：

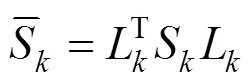
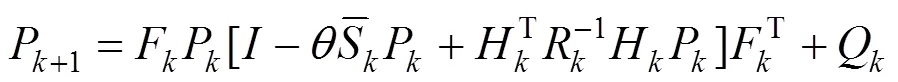
限制条件是在每步迭代计算时应满足代价函数取得极小值，即求解需要满足条件：

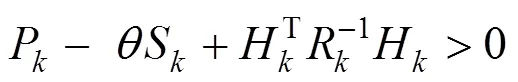
3.2 列车轨道约束模型

通过列车轨道信息对系统定位数据进行约束，其本质是将轨道信息融合到定位信息中，形成多信息融合定位，通过融合改善定位效果。

铁路轨道线路由直线、圆曲线以及连接直线与圆曲线的缓和曲线组成[19]，而曲线可以近似为由多个直线段首尾连接组成。所以，在保证所需定位精度的条件下，可在分析时人为地将列车轨道近似为由一定长度的直线段组合而成。

列车行驶具有特殊性，即列车始终行驶在轨道上，数字轨道具有相对精确的位置坐标，基于此前提可对列车进行轨道约束。列车沿直线轨道运动时，可将轨道方程表达为：

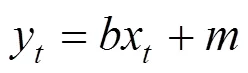
式中：y和x为轨道点的北向和东向坐标；和为直线参数。

由于列车的行驶轨迹受轨道约束，运动方向与轨道方向一致，以A和A为列车北向和东向的速度，则约束方程为[20]：

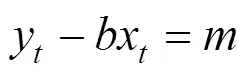
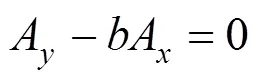
改写为矩阵形式为：

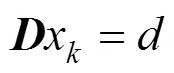
式中：为状态向量，

3.3 轨道约束的H∞滤波

直线轨道约束为线性约束，将线性轨道约束模型与H∞滤波相结合的轨道约束H∞滤波算法可提高列车的定位精度。由文献[21]的约束H∞滤波可得轨道约束H∞滤波算法。

1) 系统方程

系统的状态方程和量测方程如下：

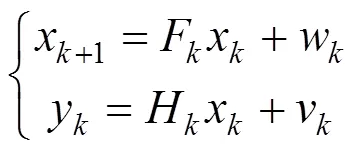
式中：和分别是过程噪声和量测噪声，为不相关的白噪声。

2) 滤波器初始化

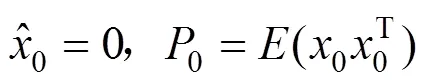
3) 每一时刻状态估计步骤

Step 1：选择可调参数矩阵。

为加权过程噪声的偏移分量。增加表示过程噪声具有更多的偏移分量，此时均方差误差性能会下降。如果0，则过程噪声为零均值，可得到卡尔曼滤波性能。

Step 2：状态估计计算。

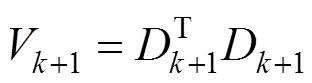
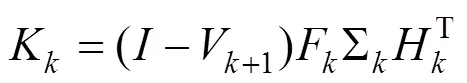
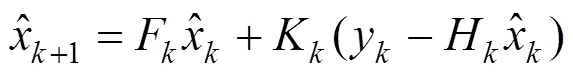
Step 3：滤波器验证条件。

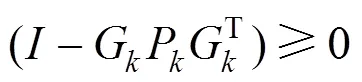
式(18)为判断H∞滤波器存在的条件。如果条件满足则回到Step 1进行下一时刻估计；如果条件不满足则滤波器无效，可以减小G并重新计算。

4 仿真验证与分析

为了验证轨道约束H∞滤波算法，采用蒙特卡罗法对典型列车定位场景进行仿真，对比卡尔曼滤波(KF)、轨道约束卡尔曼滤波(TC-KF)、H∞滤波(HF)和轨道约束H∞滤波(TC-HF)4种算法的滤波结果。

在满足一定精度的前提下，曲线段轨道可以近似为多条一定长度的直线段，并根据列车的当前位置选择相应的直线段轨道约束方程进行约束，所以采用直线段仿真不失一般性。

假设列车行驶在某段直线轨道上，方向角为60°，则列车状态向量为式(5)，列车的初始状态为：

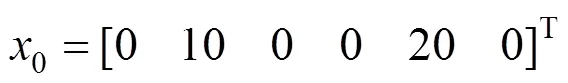
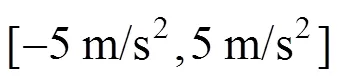
进行100次蒙特卡罗仿真实验，北向和东向不同时刻的平均距离误差分别如图1和图2所示。通过对比图1与图2可以看出，HF算法相对KF算法具有更好的稳定性和定位精度，而TC-HF算法进一步提高了定位精度，说明轨道约束可以提高滤波算法的精度。从东向的平均距离误差相对北向较大的现象中可以发现，KF算法比HF算法对噪声更敏感，而HF算法鲁棒性更好，这与HF的理论特性相 一致。

图1 东向平均距离误差

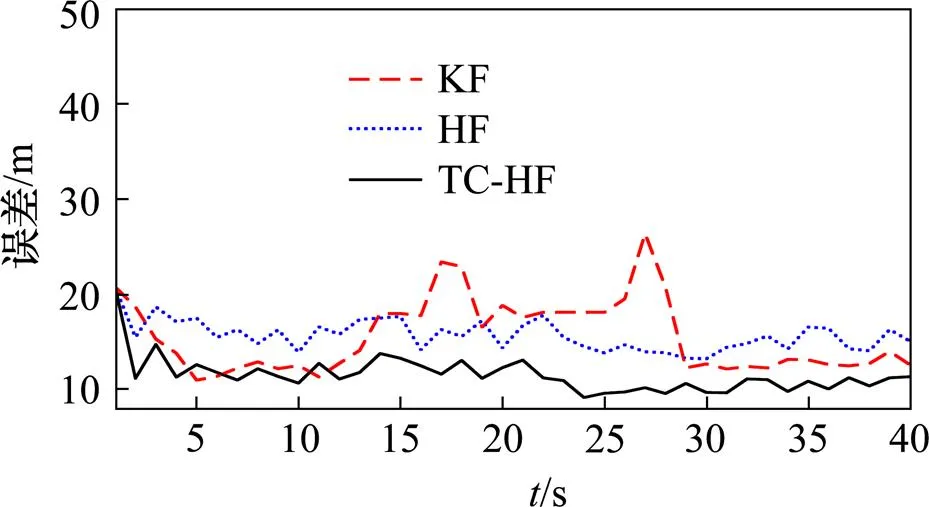
图2 北向平均距离误差

4种滤波算法仿真轨迹全程平均距离误差比较结果如图3所示，统计数据如表1所示，表1中D表示每次仿真轨迹全程平均距离误差值。

图3中，HF和TC-HF曲线相对平缓，而KF和TC-KF曲线相对突出，表示定位有失准现象发生，进一步表明了增加轨道约束的滤波算法具有更高的定位精度，而HF算法具有更强的鲁棒性，可以更好地适应列车的多变的运动状态。

表1显示，对于卡尔曼滤波算法，无约束时KF算法的平均距离误差为13.35 m，而有约束估计器平均距离误差为9.51 m，增加轨道约束后，定位精度提高了约28.7%。对于H∞滤波，有约束估计器比无约束估计器提高精度约33%。

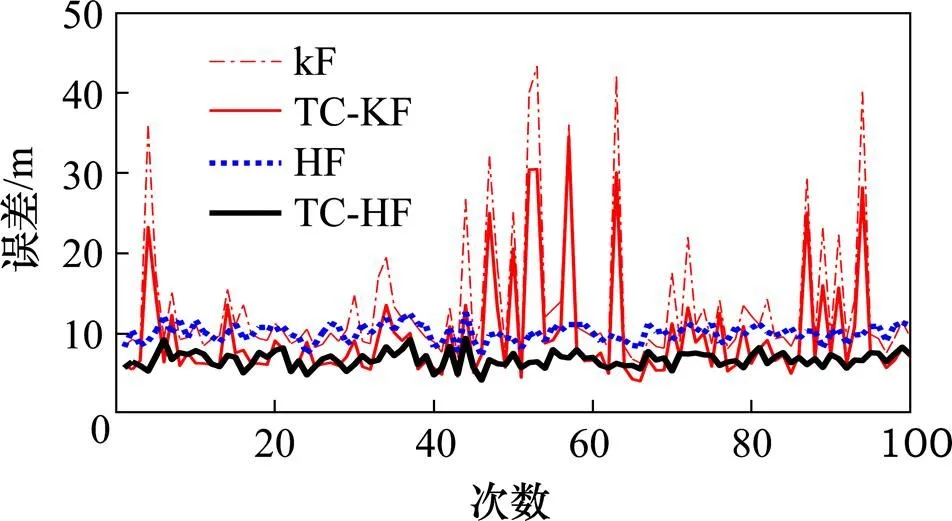
图3 100次蒙特卡罗仿真误差对比

表1 蒙特卡罗仿真统计

总体上，轨道约束后的滤波器在定位精度改善方面效果明显，H∞滤波相对卡尔曼滤波在位置估计上具有明显优势。

5 结论

1) 对加速度极值进行模糊自适应调整的“当前”统计模型可以较好地跟踪列车运行，可用于列车的实时定位。

2) 由于列车轨道及运行的特殊性，可以通过将列车轨道近似为连续直线段，建立线性轨道约束模型，仿真结果显示轨道约束可以明显提高列车定位滤波算法的位置精度。

3) 列车定位系统具有高的安全性和稳定性要求。通过对比分析轨道约束H∞滤波算法与无约束算法的定位精度误差。结果表明，H∞滤波相对卡尔曼滤波在位置估计上具有优势，验证了轨道约束H∞滤波算法的有效性。

[1] Jonáš M. GNSS integrity for railway transportation[J]. Transactions on Transport Sciences, 2011, 4(4): 183−192.

[2] Marais J, Beugin J, Berbineau M. A survey of GNSS-based research and developments for the european railway signaling[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 99: 1−17.

[3] 刘江, 蔡伯根, 王剑. 引入轨道特征的北斗列车定位方法研究[J]. 交通运输系统工程与信息, 2014, 14(5): 43−48. LIU Jiang, CAI Baigen, WANG Jian. A BDS-based train positioning method considering track characteristics[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(5): 43−48.

[4] 李卫东, 侯丽虹. 基于卫星导航系统的高速列车定位技术研究[J]. 信息与控制, 2016, 45(4): 99−106. LI Weidong, HOU Lihong. Research on high-speed train positioning technology based on satellite navigation system[J]. Information and Control, 2016, 45(4): 99−106.

[5] 曹冲. 北斗系统自主可控的国家安全命脉[J]. 中国信息安全, 2017(3): 69−72. CAO Chong. Beidou System, autonomous and controlled lifeblood of national security[J]. China Information Security, 2017(3): 69−72.

[6] 郏东耀, 黄轲. 铁路站场巡检人员多环节地图匹配定位算法[J]. 铁道学报, 2013, 35(9): 52−58. JIA Dongyao, HUANG Ke. Multi-link map-matching positioning algorithmfor inspection personnel in railway station & yard[J]. Journal of the China Railway Society, 2013, 35(9): 52−58.

[7] 李卫东, 侯丽虹, 王友生. 基于BDS/GSM-R组合列车定位方法的研究[J]. 铁道科学与工程学报, 2016, 13(3): 151−155. LI Weidong, HOU Lihong, WANG Yousheng. Study of train positioning method based on BDS/GSM-R combination[J]. Journal of Railway Science and Engineering, 2016, 13(3): 151−155.

[8] ZHAO Y. Performance evaluation of Cubature Kalman filter in a GPS/IMU tightly-coupled navigation system[J]. Signal Processing, 2016, 119(C): 67−79.

[9] Dan S. Optimal state estimation: Kalman, H infinity, and nonlinear approaches[M]. Wiley-Interscience, 2006: 250− 270.

[10] PENG C, YUE D, TIAN E, et al. Improved network- based robust H∞filtering for uncertain linear systems[J]. International Journal of Innovative Computing Information & Control Ijicic, 2009, 5(4): 961−970.

[11] 王东, 李国林. 基于鲁棒H∞滤波的GPS/INS相对导航方法[J]. 中国惯性技术学报, 2013, 21(6): 745−748.WANG Dong, LI Guolin. Robust H∞filtering for GPS/INS relative navigation[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 745−748.

[12] 邹震, 贺丰收, 缪礼锋. 基于线性约束H∞滤波的道路目标跟踪算法研究[J]. 计算机仿真, 2015, 32(6): 344− 348. ZOU Zhen, HE Fengshou, MIAO Lifeng. Road targets tracking methods research based on linear constraints H∞filtering[J]. Computer Simulation, 2015, 32(6): 344− 348.

[13] 刘友文, 刘经南, 朱敦尧. 附有道路信息约束的自适应卡尔曼滤波在车载导航中的应用[J]. 武汉大学学报(信息科学版), 2008, 33(8): 828−830. LIU Youwen, LIU Jingnan, ZHU Dunyao. Application of adaptive kalman filter restricted by road information to vehicle-borne navigation[J]. Geomatics and information Science of Wuhan University, 2008, 33(8): 828−830.

[14] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991: 135−144. ZHOU Hongren, JING Zhongliang, WANG Peide. Maneuvering target tracking[M]. Beijing: National Defence Industry Press, 1991: 135−144.

[15] 陈亮. 机动目标跟踪关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 37−40. CHEN Liang. Research on key technology of maneuvering target tracking[D]. Harbin: Harbin Engineering University, 2012: 37−40.

[16] 杨霄鹏, 欧阳超, 杨朝阳, 等. 基于“当前”统计模型的模糊自适应航迹预测算法[J]. 空军工程大学学报(自然科学版), 2015, 16(2): 1−4. YANG Xiaopeng, OUYANG Chao, YANG Zhaoyang, et al. A fuzzy adaptive algorithm based on current statistical model for track prediction[J]. Journal of Air Force Engineering University (Natural Science Edition), 2015, 16(2): 1−4.

[17] 王写. 基于H∞滤波理论和多模型算法的机动目标跟踪研究[D]. 杭州: 浙江大学, 2016: 29−35. WANG Xie. Maneuvering target tracking based on H∞filter and multi-model algorithm[D]. Hangzhou: Zhejiang University, 2016: 29−35.

[18] Ko S, Bitmead R R. State estimation for linear systems with state equality constraints[J]. Automatica, 2007, 43(8): 1363−1368.

[19] TB 10098—2017, 铁路线路设计规范[S]. TB 10098—2017, Code for design of railway line[S].

[20] DUAN W, JIA Y. A novel H-infinity filtering for road constrained target tracking[C]// IEEE, International Conference on Cloud Computing and Intelligent Systems. IEEE, 2013: 951−955.

[21] Simon D. A game theory approach to constrained minimax state estimation[J]. IEEE Transactions on Signal Processing, 2006, 54(2): 405−412.

Study on Beidou-assisted train positioning algorithm based on track constrained H∞filtering

WANG Pengfei1, 2, LI Weidong1, 3, CHU Xianwu3

(1. School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028, China; 2. Department of Mechanical Engineering, Henan Institute of Technology, Xinxiang 453003, China; 3. School of Electrical and Information Engineering, Dalian Jiaotong University, Dalian 116028, China)

Aiming at the high safety and stability requirements of train positioning, combined with the particularity of train driving, an H∞filtering algorithm using railway track information to constrain Beidou positioning data was proposed. The train motion model was established based on fuzzy adaptive “current” statistical model. By approximating the track to a straight line segment, a track constraint model was established. The track constraint model and H∞filtering are combined to realize the track constrained H∞filtering algorithm. The positioning errors of H∞filtering and Kalman filtering, constraint estimation and unconstrained estimation are compared and analyzed by simulation. The simulation results show that the track constraint is effective in improving the localization accuracy of the algorithm, and H∞filtering has robust advantages in the estimation of train position. The effectiveness of the track constrained H∞filtering algorithm is verified, and it has theoretical significance for the engineering application of Beidou-assisted train positioning.

track constraint; H∞filtering; Beidou Navigation Satellite System; train positioning

10.19713/j.cnki.43−1423/u.2019.03.033

U283

A

1672 − 7029(2019)03 − 0812 − 07

2018−05−24

国家自然科学基金资助项目(61471080)

王鹏飞(1979－)，男，河南新乡人，副教授，博士研究生，从事智能传感与测控技术研究；E−mail：muyeyunfei@163.com

(编辑 阳丽霞)