高速铁路跨线旅客列车开行方案优化研究
唐洁,杨信丰,申恒宇
高速铁路跨线旅客列车开行方案优化研究
唐洁,杨信丰,申恒宇
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
针对高速铁路跨线旅客列车开行方案展开优化研究。从旅客和铁路部门2个角度出发,以旅客出行总支出最小和铁路部门运营成本最小作为目标函数,以客流守恒定律、区间通过能力、上座率和客流需求作为约束条件,建立高速铁路跨线列车开行方案的多目标规划模型,设计该模型的遗传算法,利用MATLAB实现算法编程求解。考虑分担率变化对开行方案的影响,结合算例分别得到传统广义成本效用函数与高铁发展趋势下跨线列车开行方案的较优解,同时验证了模型和算法的有效性。
高速铁路;跨线列车;开行方案;多目标规划;遗传算法
近年来,我国高速铁路逐渐成网运营,跨线客流比例增大,跨线列车数量增加。列车的跨线开行方式,首先可以增大高速列车的服务范围,尽可能的提高旅客直达率;其次可以减少旅客的换乘时间和次数,从而降低旅客的疲劳度;最后可以减轻既有线的运输压力,提高高速线的剩余通过能力利用率,尽可能提高铁路部门收益。跨线车站的设置直接影响旅客出行方便度和上座率,同时影响铁路部门的效益。为此,针对高速铁路跨线列车开行方案的优化,相关学者开展了一系列研究。部分学者建立了单目标规划模型对其进行优化。NI等[1]以旅客车底使用数量最小为目标,以方便旅客出行和协调到发线使用为约束,设计了改进遗传算法对模型进行求解。CHEN等[2−3]在考虑到发线的协调使用的基础上,分别以旅客满意度最大、车底使用数量最小为目标建立优化模型,设计了启发式遗传算法和蚁群算法分别对问题进行求解。大多数学者通过多目标规划模型对其进行优化。ZHOU等[4]以等待时间最小和总旅行时间最小为目标建立模型,利用分支定界法和束搜索算法求解。DENG等[5]考虑运输能力,运输组织需求,旅客出行需求和旅客选择行为等因素建立优化模型。陈霞等[6−7]分别采用改进模拟退火算法、广义既约梯度算法对模型进行求解。李金梅[8]采用用户平衡理论进行了客流分配。现有文献大多以OD客流量为基础数据,从铁路运输企业和旅客两方面考虑建立多目标优化模型进行研究。通常只考虑单一跨线列车情形,没有细化跨线类型。在此基础上,本文将列车分为纯高速、纯普速、下线和上线列车4种类型进行讨论,进一步考虑高速线路与既有线之间上下线的跨线情况,并采用Logit模型进行客流分配,以旅客出行总支出、铁路部门运营成本最小为目标,建立多目标规划模型。
1 问题描述与建模
1.1 问题描述
我国高速铁路跨线行为现状:1) 不同速度等级高速列车之间跨线;2) 不同速度等级动车组之间跨线;3) 不同速度等级动车组与普速列车之间跨线。
通常情况下,根据速度对列车级别和线路级别进行分类[9]:

本文则考虑将列车分为高速列车和普速列车,同样将线路级别可分为高速线和既有线,可开行的列车类型具体如下:

国内高速铁路跨线客流的主要输送方式有跨线列车直通和中转换乘[10]。本文仅考虑以跨线列车直通为输送方式的客流直通情形,不考虑客流采用中转换乘方式出行的情形。
通常情况下列车总是上下方向成对运行,故本文只需要考虑单一方向列车的运行情况,另一方向与之相应成对出现。
1.2 符号及变量说明
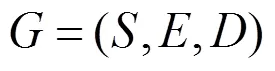

c为类列车的人公里票价率,单位为元/人· 公里;
f为类列车的车公里消耗,单位为元/车·公里;
v为类列车的旅行速度,单位为km/h;
q为区间路段e上所有客流量,单位为人;
a为类列车的列车定员数,单位为人;
n为始发站s至终到站s开行所有列车的数量,单位为列;
n为区间e上开行所有列车的数量,单位为列;
为类列车的扣除系数;
1.3 目标函数分析
1.3.1 旅客出行总支出
旅客出行主要会产生旅客票价支出和旅行时间消耗2部分支出。旅客的票价支出由人公里票价率和旅行距离决定,其中前者由列车级别和线路级别决定。通常情况下跨线列车在整个运行过程中,可能会进行不止一次的跨线行为。本文只考虑高速列车下既有线和普速列车上高速线的跨线情况,并且只进行一次跨线行为。
下面以为起讫点分析各类列车的票价支出:
纯高速列车的票价支出:

纯普速列车的票价支出:
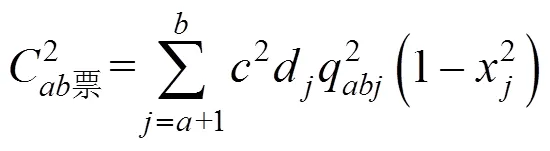
下线列车的票价支出:
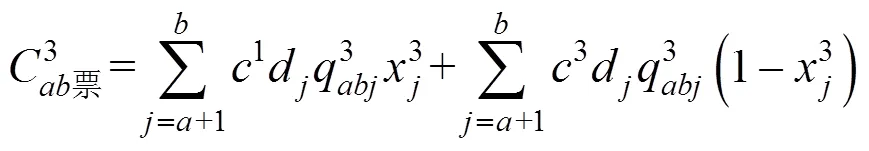
上线列车的票价支出:

旅客总的票价支出:

全线总的旅客票价支出:

列车运行时间作为旅客旅行过程中的主要时间消耗[11],主要与旅行距离和旅行速度有关。在列车运行径路已知的条件下,各区间距离是一定的,而旅行速度主要与列车、线路级别有关。
下面以为起讫点分析各类列车的旅行时间消耗。
纯高速列车上旅客的旅行时间消耗:

纯普速列车上旅客的旅行时间消耗:

下线列车上旅客的旅行时间消耗:

上线列车上旅客的旅行时间消耗:
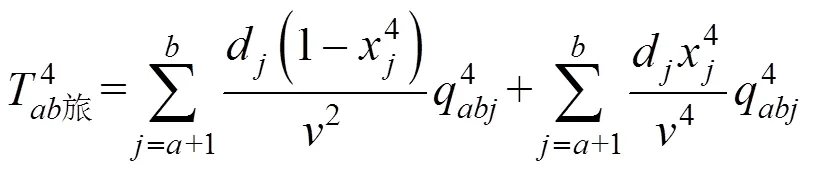
旅客总的旅行时间消耗:
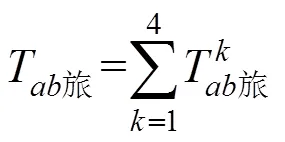
全线总的旅客旅行时间消耗:

由于旅客票价支出和旅行时间消耗的量纲不同,在进行旅客出行总支出计算时不能直接进行加和处理,故引入旅客时间价值。
全线总的旅客旅行时间消耗折合费用:

式中:为选择类列车的旅客时间价值。由于本文不考虑客流内部差异,故取为相同数值。
1.3.2 铁路部门运营成本
铁路部门的运营成本分为变动成本和固定成本,其中变动成本可以用列车的车公里消耗和旅行距离表示。列车开行的固定成本对列车开行方案不会产生影响,故不考虑固定成本[11]。本文假设列车均采用长编组,即16编组。
下面以为起讫点分析各类列车的运营成本:
纯高速列车的运营成本:

纯普速列车的运营成本:

下线列车的运营成本:


上线列车的运营成本:

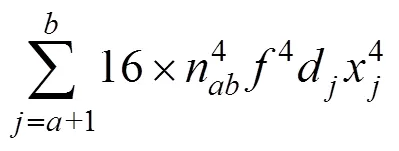
铁路部门总的运营成本:

全线总的铁路部门运营成本:

1.4 约束条件
1.4.1 满足客流守恒定律
不论客流如何分配,各个区间总的客流量保持不变,仍然满足给定的OD客流量。
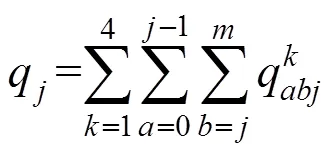
1.4.2 保证区间通过能力
为了保证线路通过能力的富余,区间占用通过能力不能超过设计通过能力的0.8。


1.4.3 保证上座率
为了保证铁路部门的运输收益,高速铁路跨线列车在各个区间的上座率必须保持在一定的范围内,上座率过低,不利于铁路部门的运营,上座率过高,不利于旅客的乘车舒适度。

表示区段上开行的始发站为s,终到站为s的类列车在运行区段的各个区间d(其中=+1,+2,…,−1,)的上座率在1~2之间。跨线列车的上座率大于等于70%才具备开行条件,故在本文研究中1取0.7;考虑到会出现列车超员的情况,并且为了保证一定的旅客舒适度,故2取1.1。
1.4.4 满足客流需求
高速铁路跨线列车的开行对数应该满足客流需求,即各个区间的跨线客流总量必须小于等于所开行的跨线列车的载客容量。

1.5 模型的建立与优化
通过以上分析,建立该问题的数学模型如下:

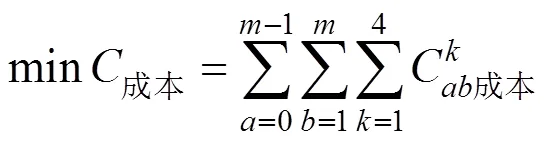






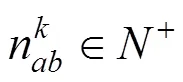
式(24)~(25)分别表示为目标函数旅客出行总支出最小和铁路部门运营成本最小,式(26)~(32)为约束条件。式(30)表示假设跨线列车只进行一次跨线行为,式(31)表示跨线列车的运行状态0-1变量,式(32)表示列车开行对数必须为正整数。
2 模型求解算法
本文构造的模型中列车开行径路是由所经过的区间路段表示,而列车经过区间路段的状态可以用0-1变量来描述,与基本遗传算法中使用二进制符号表示基因编码类似,故可以借鉴基本遗传算法,来设计新的算法来求解。列车不经过区间路段的状态可以用−1进行标记,来保证种群中染色体个体长度的一致。
算法步骤如下。


来表示。
Step 1:建立初始群体。以考虑分担率情况下确定的列车开行区段和数量为依据,生成个×矩阵的染色体个体,作为初始群体。其中,为种群大小;为区间路段数量;等于列车开行区段数乘以4(列车类型为4),表示在该种列车开行区段下,所有种类列车的开行情况数。
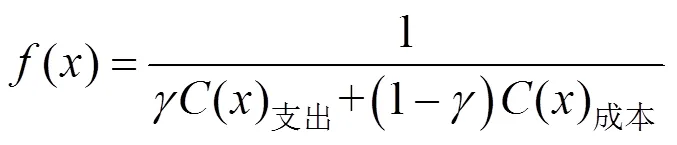
Step 3:选择算子。判断各个个体是否满足约束条件式(30),即每个运行区段的跨线列车是否满足仅进行一次跨线行为,不满足的个体直接淘汰;对于满足约束条件的个体,首先对最优个体记录并直接遗传到下一代进行保护,然后采用轮盘赌规则进行选择。依据确定的个体选择次数,整理出新的种群。


Step 6:结束判别。反复执行Step1-5,直到连续几代最优适应度值不发生变化时,终止算法,转Step7。
Step 7:还原解。根据对应与染色体编码方式解码规则对最优解进行解码操作,还原为模型中对应的解,即高速铁路跨线列车的最优开行方案。
3 算例分析
3.1 准备数据
3.1.1 站间距
假设在高速线旁边有一条与之平行的既有线,并且2条线路上对应车站之间的站间距始终相等。作为衔接站的车站s2,s4和s6每个站的高速线与既有线之间都有联络线相连,即具备跨线条件,运行路径如图1所示。

图1 运行径路示意图
其中各个车站之间的站间距如表1所示。

表1 各个车站之间的站间距
3.1.2 输送客流量
各个车站之间的日均输送客流量如表2所示。

表2 各个车站之间的日均输送客流量
3.1.3 人公里票价率及车公里消耗
不同列车类型的人公里票价率和车公里消耗如表3所示。

表3 不同列车类型的人公里票价率及车公里消耗
3.1.4 旅行速度
本文假设下线跨线列车采用300 km/h车型的动车组,即其在高速线上的实际旅行速度可达300 km/h,在既有线上的实际旅行速度为200 km/h;上线跨线列车采用250 km/h车型的动车组,在既有线上的实际旅行速度为线路允许速度160 km/h,在高速线的实际旅行速度可达250 km/h。
故在计算过程中取纯高速列车的实际旅行速度为1=300 km/h,纯普速列车的实际旅行速度为2=160 km/h,下线列车在既有线上的实际旅行速度为3=200 km/h,上线列车在高速线上的实际旅行速度为4=250 km/h。
3.2 计算
假设跨线列车采用长编组,定员为1 200人,区间通过能力富余,各站间客流OD已知,进行客流分配时,不考虑诱发客流的产生,旅客时间价值取40元/h。
3.2.1 各类列车分担率估计
运用Logit模型对选择纯高速、纯普速、下线和上线4类列车客流之间的分担率进行估计,并采用传统的广义成本效用函数进行求解[12]。
选择类列车的广义成本效用函数[13]用U表示。

式中:C为类列车的直接费用成本,元;T为类列车的旅行时间,h;E为类列车的进出站时间,h;W为类列车的等待时间,h;2,3,4和5表示各自的系数;1为常数项。
4类列车的相关数据如表4所示。其中假设上下线列车的旅行速度均以在高速线上运行速度和在既有线上运行速度的平均速度进行计算。

表4 各类列车的相关数据
计算过程中,常数项1取0;各自的系数2,3,4和5均取1;为了统一数量级,旅行时间均以列车运行100 km所花费的时间进行计算。
对于4种列车类型,采用多元Logit模型[13]。选择类列车的概率用P表示。

式中:U表示类列车的广义成本。
4类列车广义成本及分担率的计算结果如表5所示。

表5 各类列车的广义成本及分担率
3.2.2 初始方案
各区段客流密度情况如表6所示。
根据“按流开车”的基本原则,按整个方向各区段的最小客流密度依次进行开车。列车开行数量等于2站间的计划客流密度除以列车定员数,得到列车初始开行方案示意图如图2所示。
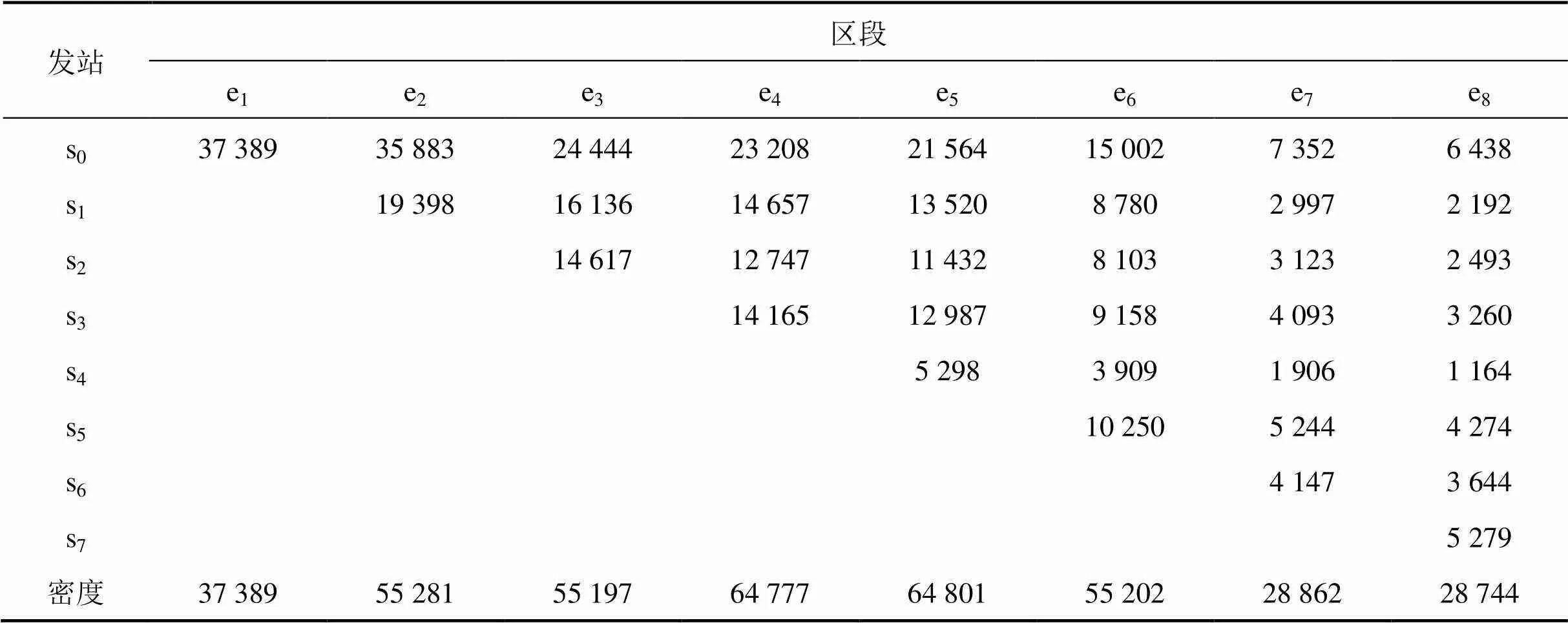
表6 各区段客流密度

图2 列车初始开行方案示意图
3.2.3 调整初始方案
不同层次客流对列车类型的选择不同,考虑4种列车的分担率,通过动态调整得到新的方案。
区段s0~s8共开行25列列车,其中纯高速6列、纯普速6列、下线6列、上线7列;区段s0~s6共开行6列列车,其中纯高速2列、纯普速1列、下线1列、上线2列;区段s1~s6共开行10列列车,其中纯高速2列、纯普速3列、下线3列、上线2列;区段s2~s6共开行5列列车,其中纯高速1列、纯普速1列、下线1列、上线2列;区段s3~s5共开行8列列车,其中纯高速2列、纯普速2列、下线2列、上线2列。
3.2.4 优化方案
计算结果界面如图3所示,各个方案的旅客出行总支出如图3(a)所示,相对应的铁路部门运营成本如图3(b)所示,迭代过程中的适应度值如图3(c)所示。

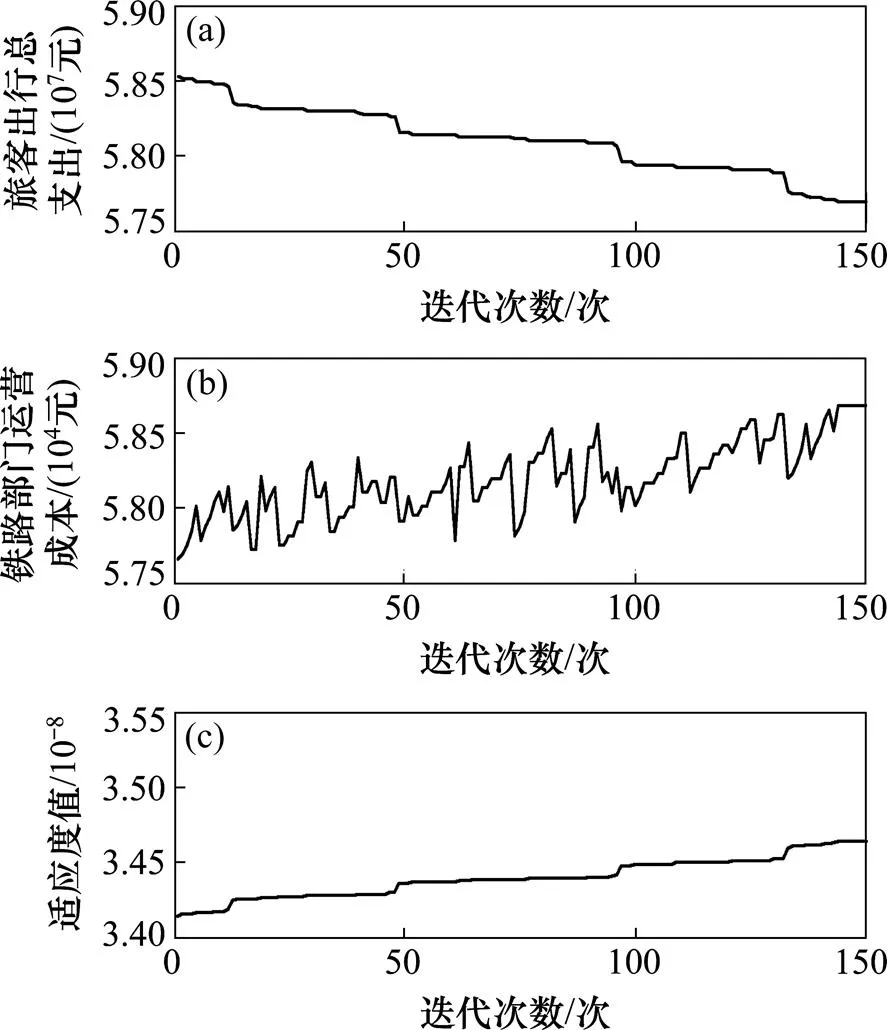
(a) 旅客运输总支出;(b) 铁路部门运营成本;(c) 适应度

图4 高速铁路跨线列车最优列车开行方案示意图
高速铁路系统逐渐完善,纯高速列车分担率将持续增加甚至超过纯普速列车,而跨线列车仍占较大比例。本文假设不同类型列车分担率:纯高速35%、纯普速15%、下线列车25%、上线列车25%条件下高速铁路跨线列车最优开行方案如表7所示。

表7 不同分担率下的列车开行方案
4 结论
1) 为了更加全面地从旅客的角度进行考虑,引入时间价值,将旅客的旅行时间消耗折合为费用和票价支出相加,作为旅客出行总支出费用。
2) 运用Logit模型对选择纯高速、纯普速、下线和上线4类列车客流之间的分担率进行估计,并采用传统的广义成本效用函数进行求解。
3) 在设计算法时,对目标函数旅客出行总支出和铁路部门运营成本最小进行线性加权处理,作为适应度函数。利用MATLAB软件进行算法编程对算例进行求解,得到较优的高速铁路跨线列车的开行方案。
本文基于一定的假设条件建立数学模型并设计算法进行求解,仍存在一些不足,如缺乏客流内部差异研究、对线路通过能力利用紧张情况以及动车组运用约束的考虑等,后期将针对不足进一步研究,完善跨线列车开行方案的优化设计。
[1] NI Shaoquan, CHEN Dingjun, LÜ Miaomiao. Research on optimization model of initial schedule of passenger trains based on improved genetic algorithm[C]// Second International Conference on Intelligent Computation Technology and Automation. IEEE Computer Society, 2009: 273−276.
[2] CHEN Dingjun, WU Kaiteng. Research on optimization model and algorithm of initial schedule of intercity passenger trains based on fuzzy sets[J]. Journal of Software, 2012, 7(1): 49−54.
[3] CHEN Dingjun, LÜ Miaomiao, NI Shaoquan. Study on initial schedule optimization model of intercity passenger trains based on ACO algorithm[J]. International Journal of Advancements in Computing Technology, 2011, 3(4): 222−228.
[4] ZHOU Xusong, ZHONG Ming. Bicriteria train scheduling for high-speed passenger railroad planning applications[J]. European Journal of Operational Research, 2005, 167(3): 752−771.
[5] DENG Lianbo, ZENG Qiang, GAO Wei, et al. Optimization of train plan for urban rail transit in the multi-routing mode[J]. Journal of Modern Transportation, 2011, 19(4): 233−239.
[6] 陈霞. 高速铁路跨线列车运行方案优化研究[D]. 成都: 西南交通大学, 2017. CHEN Xia. Study on optimization scheme of cross-line train for high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2017.
[7] 周鹏飞. 高速铁路跨线客流输送模式研究[D]. 北京: 北京交通大学, 2015. ZHOU Pengfei. Research on the cross-line passenger flows transportation modes on high-speed railways[D]. Beijing: Beijing Jiaotong University, 2015.
[8] 李金梅. 高速铁路周期性列车开行方案的优化研究[D]. 北京: 北京交通大学, 2015. LI Jinmei. Research on cyclic train line planning for high-speed railways[D]. Beijing: Beijing Jiaotong University, 2015.
[9] 田松江. 高速铁路跨线列车开行方案优化研究[D]. 成都: 西南交通大学, 2014. TIAN Songjiang. High-speed railway cross-line train working plan optimization research[D]. Chengdu: Southwest Jiaotong University, 2014.
[10] 屈明月. 高速铁路成网条件下客流输送模式研究[D]. 成都: 西南交通大学, 2014. QU Mingyue. Research on the passenger transportation mode of high-speed railway network[D]. Chengdu: Southwest Jiaotong University, 2014.
[11] 彭其渊. 高速铁路运输组织基础[M]. 成都: 西南交通大学出版社, 2014: 28−29. PENG Qiyuan. Foundation of high-speed railway transportation organization[M]. Chengdu: Southwest Jiaotong University Press, 2014: 28−29.
[12] 张晓宇. 高速铁路列车开行方案关键要素对客运需求的影响研究[D]. 北京: 北京交通大学, 2016. ZHANG Xiaoyu. Influence research of the key factors of operation plan on passenger demand at the high-speed railway[D]. Beijing: Beijing Jiaotong University, 2016.
[13] 闫海峰. 客运专线旅客列车开行方案优化[M]. 成都:西南交通大学出版社, 2012: 31−32. YAN Haifeng. Passenger train line passenger train plan optimization[M]. Chengdu: Southwest Jiaotong University Press, 2012: 31−32.
Optimization study on high-speed railway cross-line passenger train plan
TANG Jie, YANG Xinfeng, SHEN Hengyu
(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)
To study the high-speed railway cross-line passenger train plan, the optimal solution was carried out. From the perspectives of both passengers and railway departments, taking the minimum total expenditure of traveling passengers and the minimum operating cost of railway department as the objective function, and taking the conservation laws of passenger flow, interval through ability, attendance and passenger flow volume demand as the constraint conditions, the multi-objective planning model was established. The corresponding genetic algorithm was designed, which was realized by MATLAB. Considering the influence of the change of share rate on the train plan, the optimal solutions for cross-line train plane based on the traditional generalized cost function and the development trend of high-speed railway are obtained, respectively. The validity of the model and algorithm is verified as well.
high speed railway; cross-line train; train plan; multi-objective programming; genetic algorithm
10.19713/j.cnki.43−1423/u.2019.03.006
U292.3+5
A
1672 − 7029(2019)03 − 0596 − 09
2018−04−03
国家自然科学基金资助项目(71761024)
杨信丰(1978−),男,河南开封人,教授,博士,从事交通运输系统组织理论方法研究;E−mail:xinfengyang@mail.lzjtu.cn
(编辑 涂鹏)

