不同车道被占用时通行能力的影响因素分析
于玲, 荚丝雨, 孙宝芸
(沈阳建筑大学 交通工程学院, 辽宁 沈阳 110168)
交通拥堵是城市交通治理不变的热点和核心问题。车道往往会因为交通事故等原因被占用,从而降低了道路的通行能力,严重的话会导致交通堵塞。为了帮助交通管理部门更好地管理城市交通,需要正确估算车道被占用对城市道路通行能力的影响程度。
以沈阳某城市次干路发生交通事故为例,主要分析交通事故发生后,事故所占车道不同对道路的实际通行能力是否存在不同影响。利用自动摄像机采集交通流情况,统计出不同车道被封闭时每一信号周期内通过事故断面的车辆类型与数量,得到两种封闭情况下的实际通行能力对比图,并用VISSIM仿真软件对影响道路实际通行能力的因素进行逐一分析。研究结果可为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供参考。
1 封闭不同车道时的实际通行能力
为了正确估算车道被占用对城市道路通行能力的影响程度,为交通管理部门正确引导车辆行驶提供理论根据。首先需要建立交通事故期间事故发生点所处横断面的理论通行能力模型,并对理论通行能力进行系数修正,从而建立道路实际通行能力随时间变化的序列模型,进而计算得到各时间段内的实际通行能力数值。
1.1 建立单车道的理论通行能力模型
C0=1 000v/hd
(1)
式中:hd为连续车流的最小车头间距(m);v为车辆行驶速度(km/h)。
hd=L0+L1+U+I×v2
(2)
式中:L0为停车时的车辆安全车间距(m),取2 m;L1为车辆长度(m),取5 m;I为与车重、路面阻力系数、黏着系数及坡度有关的系数(表1);U为驾驶员在反应时间内车辆行驶的距离(m),U=v×t,t≈1.2 s。
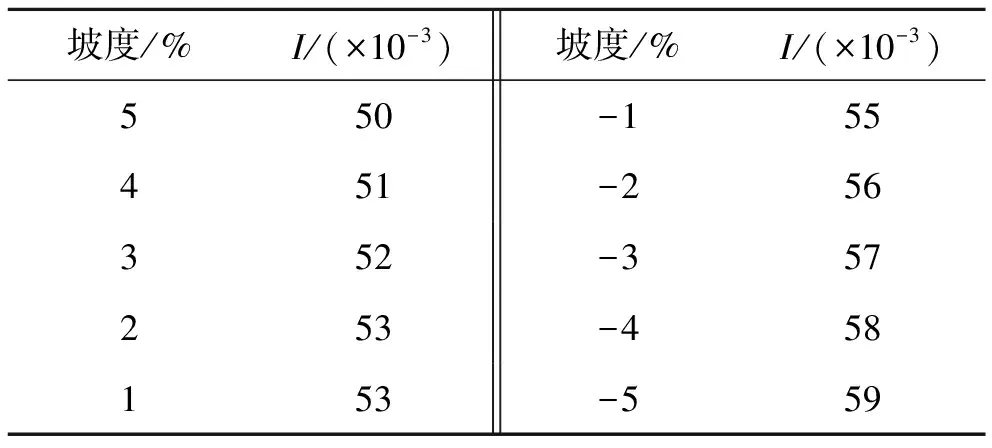
表1 参数I与坡度的关系
将式(2)代入式(1),并换算单位,得:
(3)
依据表1,选取I值为0.054。理想交通条件下小客车的车速为60 km/h,因此v取60 km/h。将数值代入到式(3)中,经计算,得C0=1 429 pcu/h。
1.2 建立多车道的实际通行能力模型
C路段=C0×n×α公交车×α电瓶车×α车道
(4)

表2为车辆换算系数,表3为车道宽度折减系数。

表2 车辆换算系数
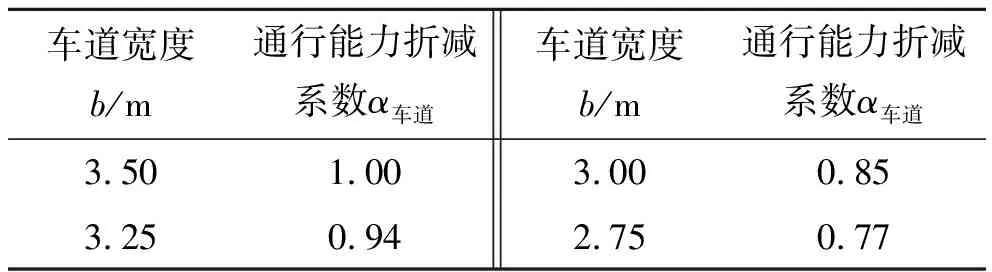
表3 车道宽度折减系数
整理得到多车道的实际通行能力函数表达式为:
(5)
根据路网情况,依据表2、3选取数值代入到式(5)中,得:
(6)
1.3 两种封闭情况的实际通行能力计算
城市道路中常发生的交通事故类型有追尾、碰撞、抛锚等,研究路段中两辆小轿车横跨两个车道发生碰撞,导致事故断面只能通过一个车道宽度的车流。该文研究路段为沈阳某城市次干路,事故发生在双向六车道中央分隔带一侧的单向三车道上。对事故导致二、三车道被封闭时道路通行能力和事故导致一、二车道被封闭时的道路通行能力进行对比研究。
如图1、2所示,事故导致两条车道被占用,只有一条车道可以通行,被占车道上的车须变道才可通行。图1中的车道优先级为车道一、二、三,即车道三上的车辆需先变道到车道二,车道二上的车辆需要变道到车道一后车辆才可以通过事故断面。图2中的车道优先级为车道三、二、一,即车道一上的车辆需先变道到车道二,车道二上的车辆需要变道到车道三后车辆才可以通过事故断面。由于可供通行车道的数量锐减,因此在事故地点处产生瓶颈路段,导致产生排队现象。

图1 封闭二、三车道时的瓶颈路段
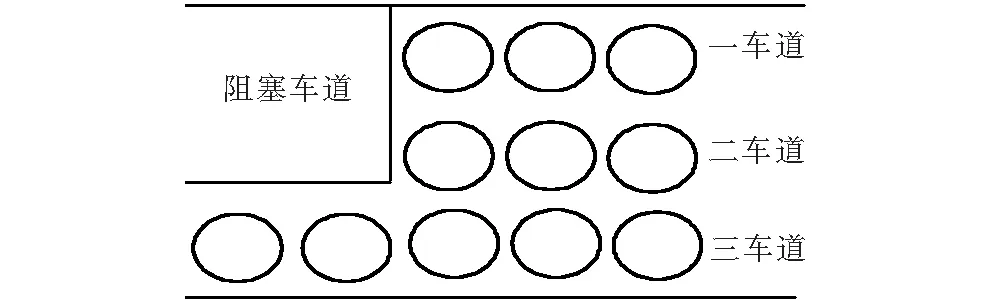
图2 封闭一、二车道时的瓶颈路段
采取人为查数方法,确定交通事故发生后每1 min内通过事故断面的车辆类型与数量。之所以选择1 min,是因为上游交叉口信号周期为60 s,如果选取30 s的话,上游路口会出现数量上升下降的周期性,不便于数据分析。由于视频中出现了一些卡顿、暂停、跳变、镜头拉伸的现象,这些现象使图像处理后的结果不稳定,需要对这部分视频信息进行剔除。从事故发生到事故解除,共历时13 min,以60 s为单位,取13组数据,对通过事故断面的所有电瓶车、公交车、小汽车的数量进行记录,计算出电瓶车和公交车的混入率,代入式(6)中,最终得到两种封闭车道情况下的实际通行能力数值,如表4、5所示。
对比表4、5可以发现:封闭一、二车道时的实际通行能力往往要稍好于封闭二、三车道时的实际通行能力。由此可得:交通事故发生在道路的不同位置,对道路横断面实际通行能力的影响存在差异。
2 封闭不同车道时道路实际通行能力不同的影响因素分析
沈阳某城市次干路封闭不同车道后其实际通行能力不同,下文将对其可能的影响因素进行分析,并采用VISSIM仿真软件对研究内容进行验证。

表4 封闭二、三车道时的实际通行能力

表5 封闭一、二车道时的实际通行能力
为还原真实路网,在模型中进行了信号配时、冲突区域、行车速度、跟车模型、交通量输入、路径决策的设置,选取了所需的评价指标,如延误时间、平均行程时间、排队长度、数据统计等,建立路段交通微观仿真系统动态模型。
2.1 车流量的影响
采取人为查数法统计通过上游交叉口进入事故路段的车辆类型与数量发现,两种封闭情况下的交通量不同。封闭二、三车道时的平均交通量为1 123 pcu/h,封闭一、二车道时的平均交通量为1 565 pcu/h。因此首先考虑是否是交通量导致两种封闭情况下的道路实际通行能力不同。利用VISSIM仿真软件还原路网情况,并在两种封闭情况下输入相同的交通量1 500 pcu/h。由仿真软件直接输出评价结果,得到两种封闭车道情况下的平均延误和平均行程时间,如表6所示。

表6 不同车道被占用时的评价指标数值对比
由表6可知:封闭一、二车道时的平均延误和平均行程时间都要比封闭二、三车道时小很多,因此可得:在车流量相同的情况下,封闭一、二车道时的道路实际通行能力要好于封闭二、三车道时,车流量不是导致封闭不同车道时道路实际通行能力不同的因素。
2.2 上下游交叉口的影响
如图3所示,事故发生点距离上游交叉口240 m,上游交叉口右侧道路禁左,则上游交叉口右侧无车辆进入到研究路段;交叉口左侧车道不受信号控制允许有车进入研究路段,但是据观察,此方向来车较少,可以忽略。因此,上游交叉口对研究路段不同车道被封闭时的道路通行能力没有影响。事故路段距离下游交叉口距离较远,因此不受下游交叉口路况影响。经过分析得到结论:上下游交叉口对不同车道被封闭时的道路通行能力不存在影响。

图3 上游交叉口交通组织方案
2.3 下游路口转向比例的影响
该路网事故路段下游路口转向比例为右转∶直行∶左转=21∶44∶35,但无论车辆的转向意图如何,都需要从事故断面处未封闭的车道排队通过。即车辆从上游交叉口通过驶入事故路段一定距离后即发现前方排队情况,因此还未根据自身转向意图进行变道便进入排队状态。因此推断下游转向比例对不同车道被占用时的道路通行能力不存在影响,利用VISSIM道路仿真软件对该结论进行了验证。
2.4 支路的影响
研究路段中的支路与主路的关系类似于入口匝道与高速公路的连接关系,参照文献[6]分析了支路对主路通行能力的影响。
“当发生交通事故时,驾驶员常常在驶入匝道和一号车道之间变换交汇点,实际的交汇形式是变化的,但是它将对主干道和匝道的排队长度产生严重的影响。对于合流,从匝道来的车辆寻找临近主线上交通流中可用的间隙以便汇入。由于绝大部分匝道在主线的右侧,因此主线上右侧车道是主线车道中最直接受影响者。汇入的车流与过境车流之间是相互影响的,同时汇入车流对高速公路整个方向车流的运行具有相当大的影响。”
由此可知:车辆从支路汇入一车道和汇入三车道时的交汇点以及可用的汇入间隙是不同的,因此初步判断支路对不同车道被占用时的道路通行能力存在影响。利用VISSIM仿真软件对推断进行验证,其结果如表7所示。
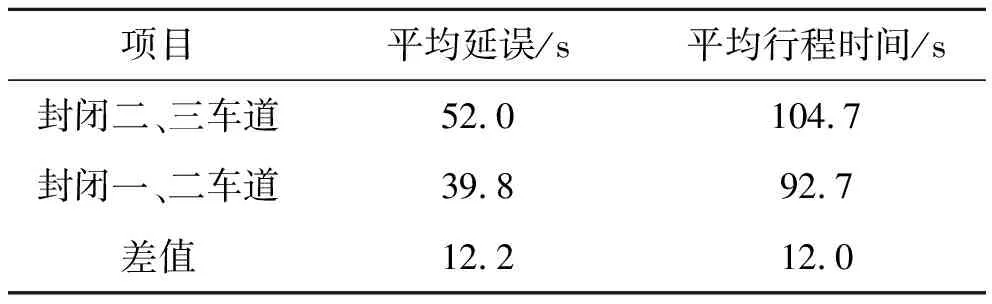
表7 不同车道被占用时的评价指标对比(有支路)
由表7可知:封闭一、二车道时的平均延误和平均行程时间要比封闭二、三车道时小很多。经过对考虑因素逐一分析发现只有支路对封闭不同车道时的道路通行能力是有影响的,且支路影响下封闭一、二车道时的通行能力较好,这与两种不同封闭方式下实际通行能力的分析结果一致,说明仿真结果正确。
因此可以得到如下结果:车流量不是导致封闭不同车道时道路实际通行能力不同的因素,上下游交叉口和下游交叉口转向比对不同车道被封闭时的道路通行能力不存在影响,支路对不同车道封闭时的道路通行能力是有影响的。
3 结论
(1) 建立了实际通行能力模型,根据实际路网情况对理论通行能力模型进行了修正,得到两种封闭车道情况下的实际通行能力数据,发现封闭一、二车道时的通行能力要好于封闭二、三车道时。
(2) 对于交通量、上下游交叉口、下游路口转向比例、支路对于封闭不同车道时的道路通行能力是否存在影响进行了分析,最终发现封闭一、二车道时的通行能力要好于封闭二、三车道时的通行能力的原因是因为支路的作用。研究结果不仅对城市道路具有参考性,同时可以推广到其他等级公路中,即当因施工或事故等原因需要对道路进行部分封闭时,封闭靠近路基边一侧的车道对道路的通行能力影响较小。

