基于B样条曲线逼近的边坡临界滑动面的混合启发式搜索算法

苗晓燕，陈昌富

(湖南大学 土木工程学院，湖南 长沙 410082)

1 引言

临界滑动面的合理确定是边坡稳定性分析的关键。传统滑动面形状常人为假设为直线形、圆弧形、对数螺旋形、二次抛物线形等，而工程实践中受边坡几何形状各异、材料特性多变的影响，滑动面形状并不完全规则。因此，采用任意形状滑动面更具客观性与广泛适用性，且因滑动面形状所受约束较少，往往能搜索到更接近实际的临界滑动面和安全系数值。任意形状滑动面的构造一般采用若干点将滑动面曲线离散，点间通过直线或曲线相连，点的坐标作为优化变量。显然，离散点越多滑动面模拟精度越高，但相同模拟精度要求下，折线模式所需离散点个数要大于曲线模式，应用曲线模拟任意形状滑动面相比折线具有优化变量少、搜索效率高的优势。陈祖煜、李亮等，采用三次样条插值函数较好地模拟了边坡任意形状滑动面。但是，插值样条要求曲线必须通过全部控制点，其合理性较大依赖于控制点本身的精确度。而控制点坐标作为优化变量，结果具有一定的随机性，更多地代表的是一种趋势和走向，此时，要求拟合曲线严格通过控制点意义不大，滑动面的非凸性也难以保证，且计算公式较复杂。更合理的做法应是，利用三次B样条构造一条曲线使之整体上最大程度地逼近控制点构成的特征多边形。B样条是当前工业几何设计和形状数学描述中表示和设计自由曲线的主流方法。三次B样条具有三次插值样条的光滑度，同时由于其曲线包含在控制多边形内，便于将控制多边形作为边界来约束滑动面形状。当控制多边形为凹形时，滑动面满足非凸性；当相邻4个控制点共线时，其对应曲线段退化为一直线段，可模拟直曲组合滑动面。其中，三次均匀B样条因几何性质优良、公式简明易行应用广泛。

20世纪70年代以来，大量学者分别引入各种优化方法搜索边坡临界滑动面。它们相比传统手动试算或经验方法，人工计算量大大减轻，成果更为准确可靠。蚁群算法、粒子群算法、遗传算法等启发式算法以其强大的全局搜索能力、广泛的适用性成为近年来的研究热点。2009年，Rashedi等提出一种新的启发式算法——万有引力搜索算法(Gravitational search Algorithm，GSA)。该算法通过模拟物理学万有引力定律实现种群优化，它拥有强大的全局搜索能力，性能优于常见的粒子群算法和遗传算法。蒋建国等研究发现，GSA在边坡临界滑动面搜索中具有很好的应用前景，有待深入研究。GSA作为一种全局优化算法，也存在易陷入局部最小的通病，结合其他算法思想和优化策略进行组合改进是提升算法优化性能的有效途径。该文采用三次均匀B样条函数模拟边坡任意形状滑动面，采用Morgenstern-Price法(M-P法)计算滑动面对应安全系数。然后将启发式算法中的GSA与PSO相融合，引入雁阵效应和非线性惯性权重进行改进，提出一种新型混合启发式搜索算法(Hybrid Heuristic Algorithm，HHA)，以安全系数为目标函数，对边坡临界滑动面进行搜索。最后通过四道标准考题来验证该文方法的可靠性。

2 边坡任意滑动面模拟方法

2.1 控制点序列与优化变量

将滑动面用N个点P1、P2,…,PN离散(滑入点为P1，滑出点为PN)，作为控制点序列，则在平面内，控制点的位置矢量共含2N个未知变量(xP1，yP1，…，xPN，yPN)。若直接将所有未知变量作为优化变量，存在工作量大、效率低的问题。为精简优化变量，以坡脚为原点建立直角坐标系，将控制点等横间距布置，则当x1、xN确定后，xi(i=2，3，…，N-1)均可知，且有y1=0，yN=H+(xN-H/tanβ)tanε，优化变量降至N个，即(xP1，yP2，yP3，…，yPN-1，xPN)。

2.2 三次均匀B样条曲线的生成

当控制点坐标确定后，代入三次均匀B样条表达式即可生成样条曲线模拟的滑动面。三次均匀B样条曲线由多个三次多项式构成的曲线段分段拼接而成，每个曲线段由基函数与相邻4个控制点的线性组合唯一确定。该表达式不含导数，较插值样条函数更加简单、便于实现。第i段的表达式为：

(1)

式中：Si(u)为第i段B样条曲线上任一点的位置矢量，即[xi(u)，yi(u)]；Pi为控制点序列中第i点的位置矢量，即[xPi，yPi]；u为[0,1]区间内参变量，以Δu的速度从0增至1，该文取Δu=0.001，即令每个曲线段由1 000个点组成。

2.3 曲线端点的处理

由于三次均匀B样条曲线始于第二个控制点附近，终于倒数第二个控制点附近[图1(a)]，故为保证曲线能完整拟合滑动面，在离散点首尾分别补充一个边界点P0、PN+1，控制点总数变为N+2个。边界点坐标一般参照离散点的间距和方向设置，不影响优化变量个数。但常规的边界点设置只能使曲线端点位于首尾离散点附近，无法使二者重合，导致样条曲线的端点不能刚好落在坡底和坡顶平面上。为解决这一问题，同时保持曲线在起点和终点的光顺性，根据文献[11]，该文给出一种较好的端点处理方法。

B样条曲线的起点处，有S0(0)=P1，即：

P0+4P1+P2=6P1

(2)

设P2=η0P0，解得P0的位置矢量为：

(3)

B样条曲线的终点处，有SN-2(1)=PN，即：

PN-1+4PN+PN+1=6PN

(4)

设pN+1=η1PN-1，解得PN+1的位置矢量为：

(5)

上述处理后，B样条曲线的起、终点分别与首末离散点重合，且曲线保持光滑[图1(b)]。

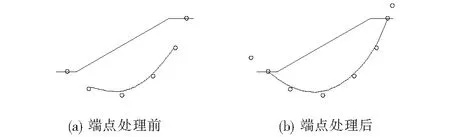
图1 三次均匀B样条曲线端点处理

2.4 滑动面合理性控制

借鉴文献[2]、[5]、[12]、[13]的滑面生成策略并结合B样条曲线的凸包性，通过对控制点变量的初始化和边界条件进行约束，保证生成滑动面的合理有效，无须二次修复或筛选。

如图2所示，滑入点x1与滑出点xN按常规的常数上下限[x1min，x1max]、[xNmin，xNmax]约束。x1与xN在约束范围内随机确定后，均分相邻控制点的水平间距得Δx=(xN-x1)/(N-1)，则其余控制点的横坐标xi均可知。纵坐标yi的约束条件较复杂，直观来看，yi的上限不能超过坡面，下限不能低于基岩fs(xi)，若不存在基岩可人为设定一个较大负值，如-H等。设相邻控制点间线段PiPi+1的水平倾角为αi(水平线下为负)，为不生成锯齿状滑面，须保证αi≥αi-1，故tanαi≥tanαi-1，即(yi+1-yi)/Δx≥(yi-yi-1)/Δx，化简得到yi+1≥2yi-yi-1。同时，为避免前面的搜索参数取某些值后，后面的搜索参数在约束条件下可行域为空集的情况，连接控制点Pi、PN交直线x=xi+1于Mi+1点，其纵坐标为yMi+1，应保证yi+1≤yMi+1，否则后面的滑动面必然出现凹陷。根据相似三角形原理，(yMi+1-yi)/(yN-yi)=1/(N-i)，解得yi+1≤yi+(H-yi)/[N-(i-1)]。需要说明的是，由于已知y1为0，yi的搜索实际从i=2开始。此时，线段P1P2的水平倾角α1是滑动面生成的初始方向，根据经验，α1满足-45°≤α1，所以-Δx≤y2，又因为线段P1PN交直线x=x2于x轴以上，故当x2≤0时，只需不超过坡面y=0即可。综上，yi的约束范围如表1所示。

图2 控制点取值范围

表1 控制点纵坐标yi的约束范围

3 混合启发式搜索算法(HHA)

3.1 混合启发式搜索算法(HHA)思想

GSA算法中，粒子被视为一组在多维搜索空间无阻力运动的有质量物体，粒子的位置代表优化变量，每个位置对应的优化问题的目标函数值称为适应值，粒子的质量代表该位置适应值的优劣，适应值越佳的粒子惯性质量越大。粒子遵循万有引力定律更新速度和位置，朝大质量粒子趋近，逐渐逼近最优位置对应的最优解。GSA具有较强的全局搜索能力和收敛速度，但也存在易陷入局部最小和解精度不高的问题。为此，该文结合粒子群算法PSO、雁阵效应及非线性惯性权重对其进行改进，得到一种新型混合启发式搜索算法(Hybrid Heuristic Algorithm，HHA)。

GSA每次迭代时，粒子的位置都会更新，粒子群到达过的较优位置不能被保留。虽然迭代历史上的种群最优都会被记录，对比后得出最终解，但在粒子移动过程中，粒子的速度和位置更新仅依据当前引力，不能学习粒子个体和群体的有益经验，算法收敛速度较慢、解精度不高。而粒子群算法在速度的更新中，通过跟踪个体最优和群体最优实现了对粒子记忆信息的有效利用。采用粒子群算法的记忆功能改进万有引力算法，粒子的速度公式为：

(6)

然而改进后，由于受全局最优的强烈吸引，粒子群在搜索后期趋向同一化。要想为群体输入新鲜信息，就要增加种群数量或降低对全局最优的追逐。增加种群数量会加大计算量，而减弱对全局最优的追逐又使算法不易收敛。为在保持粒子多样性的同时减少代价，受自然界雁阵效应启发，将粒子按个体最优适应值排序，最佳的粒子作为头雁，依靠其自身飞行经验决定下一步的运动，其他粒子依次跟随其前方较优粒子飞行。每次迭代后，更新粒子群的历史最优适应值，并重新排序。这样就使粒子群不止朝一个方向运动，保持了粒子的多样性。综合雁阵效应和粒子群记忆功能，最终可得混合启发式搜索算法(HHA)的速度公式为：

(7)

由式(7)可知，粒子当下速度以r0的比例继承于先前速度，这种继承能力的大小影响算法的全局探索和局部开发能力。当r0较大时，算法全局探索能力增强，但局部开发能力减弱，相同迭代次数的最优解精度较差；当r0较小时，算法局部开发能力增强，但全局探索能力减弱，在优化前期易陷入局部最优。为更好地平衡算法的全局探索能力和局部开发能力，引入非线性惯性权重函数代替随机数来体现继承能力：

r0=ws-(ws-we)(t/T)2

(8)

式中：ws为初始惯性权重；we为最大迭代次数的惯性权重，通常取ws=0.9、we=0.4时算法优化性能最好；t为当前迭代次数；T为最大迭代次数。由式(8)可知，r0随迭代次数逐渐下降，且前期下降较慢，后期下降较快。由此可保证算法在迭代前期着重于全局搜索，而后期着重于局部开发。

3.2 混合启发式搜索算法(HHA)流程

(1)确定搜索空间，生成初始种群。设在d维搜索空间中存在N个粒子，第i个粒子的位置为：

(9)

(3)计算并更新粒子质量。定义第i个粒子t时刻的惯性质量为：

(10)

式中：fiti(t)为第i个粒子t时刻的适应值；best(t)、worst(t)分别为t时刻种群最优和最差适应值。

(4)计算并更新万有引力。由万有引力定律，t时刻粒子i受粒子j在第d维上的引力为：

(11)

Ri,j(t)=‖xi(t)，xj(t)‖2

(12)

G(t)为t时刻万有引力常数，其值随宇宙实际年龄的增大而变小，表达式为：

G(t)=G0×e-αt/T

(13)

式中：G0为t0时刻的G值，通常取100；α为衰减系数，通常取20；T为最大迭代次数。

(5)计算合力。t时刻，惯性质量最大的前k个粒子集合作用于粒子i第d维上的合力为：

(14)

式中：randj为[0,1]之间的随机数，可使搜索具有一定的随机性而更加合理；kbest为惯性质量最大的前k个粒子集合，其初值为N，随时间t线性减至1。

(6)更新粒子的加速度、速度和位置。由牛顿第二定律，t时刻粒子i在第d维产生的加速度为：

(15)

速度更新公式见式(7)、(8)，位置更新公式为：

(16)

3.3 数值试验验证

为评估HHA的优化性能与效率，对比文献[10]中8个经典测试函数进行数值试验，结果如表2所示。MGSA为文献[10]改进GSA算法。表中，F1、F2、F3、F4为单峰函数，其余为多峰函数。函数维数均为30，全局最小真值均为0。参数G0=100，N=50，α=40，itmax=1 000。每个函数计算30次。

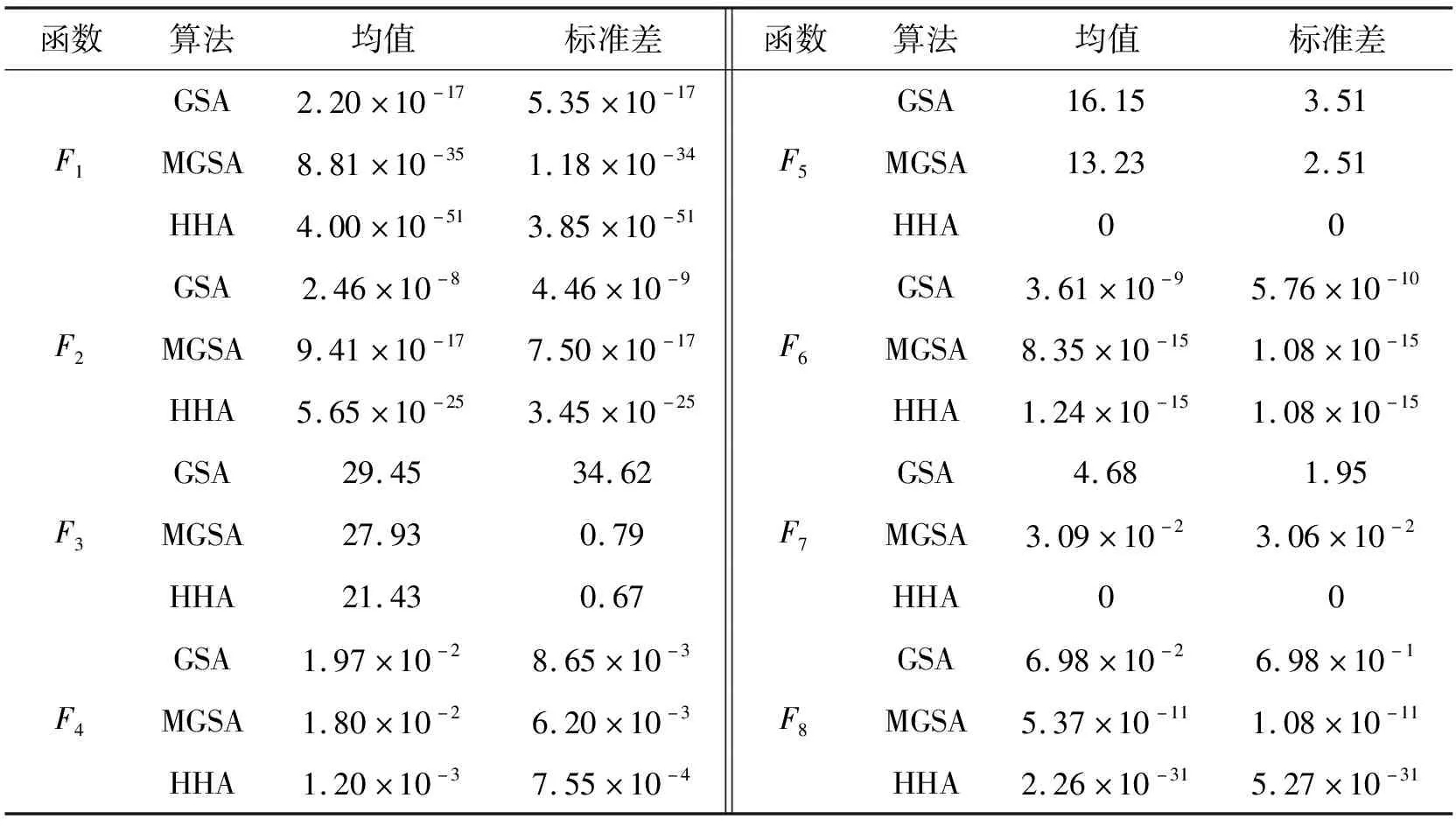
表2 测试函数不同算法优化性能对比

注：表中GSA、MGSA的计算结果源自文献[10]。

对比表2均值可知：HHA的优化精度较GSA有数量级的提升，改进效果优于MGSA。说明HHA能有效跳出局部最优，具有更好的收敛精度。再对比表2标准差可知，HHA的标准差最小，稳定性优于GSA与MGSA。

由于HHA相比GSA增加了计算步骤，为评估HHA算法的效率，以F1函数为例，比较等精度要求下的算法耗时。设误差要求控制在5%以内，HHA只需迭代50次，耗时0.96 s，而GSA需迭代500次以上，耗时大于3.6 s，可见等精度要求下HHA优化效率更高。

综上所述，HHA能有效克服GSA易陷入局部最小的不足，具有更好的优化精度、效率与稳定性。

3.4 基于HHA的边坡稳定性分析

由三次均匀B样条函数生成有效的任意形状滑动面后，采用计算严密、收敛性好的M-P法计算滑面对应的安全系数Fs。再以安全系数为目标函数，根据3.2节流程采用HHA算法搜索得到边坡临界滑动面及对应的最小安全系数。

M-P法中边坡的条分方式和条块受力如图3所示。目标函数Fs的计算公式为：

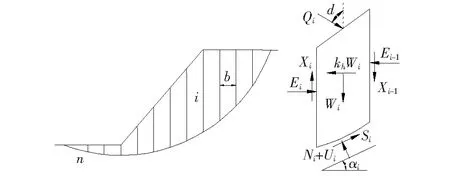
图3 边坡土条受力分析

(17)

式中：

(18)

其中比例因子λ按下式计算：

λ=

(19)

而Ei通过以下递推公式得到：

(20)

4 算例验证

选取澳大利亚计算机应用协会(ACADS)的4道边坡稳定标准考题，应用样条逼近生成滑动面并采用M-P法计算安全系数，再以安全系数为目标函数，分别采用GSA与HHA搜索临界滑动面，与推荐答案进行对比。其中，考题1(a)为均质边坡，考题1(c)为非均质边坡，考题1(d)在考题1(c)基础上土体水平方向增加一系数为0.15g的地震加速度，为考虑地震效应边坡，考题3(a)为含软弱夹层边坡。

题中边坡的几何形状与剖面尺寸见图4，材料特性如表3所示。为平衡搜索效率与滑动面模拟精度，考题1(a)中离散点取7个，考题1(c)、1(d)中离散点取9个，考题3(a)中离散点取11个，条分数均为20。GSA与HHA中种群数为50，总迭代次数为200，HHA中c1=c2=c3=0.5。计算结果及推荐答案列于表4。

由表4可知：考题1(a)、1(c)、1(d)中，该文方法的计算安全系数均与文献推荐答案较为接近，相应的临界滑动面与文献圆弧滑动面形状相似、位置相近，证明三次均匀B样条能合理逼近圆弧滑动面，GSA与HHA对于均质边坡、非均质边坡及考虑地震效应边坡的滑动面搜索均适用。且HHA的优化结果比GSA更小，优化性能更佳。

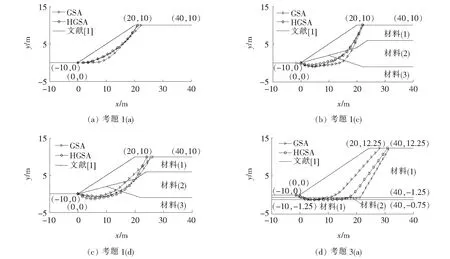
图4 临界滑动面对比

表3 考题材料参数

考题3(a)为典型的滑动面沿软弱夹层呈非圆弧状的边坡，由于该文不对滑动面直线段预先假定，且土体的软弱夹层很薄(0.5 m)，控制点个数又多(11个)，故临界滑裂面的搜索非常困难。此时，GSA显然难以胜任，最优解停留在1.6左右，远大于推荐答案，滑动面位置也相距较远。而HHA的安全系数依然接近并略小于推荐答案，二者滑动面位置相近，形状吻合，特别是在软弱土层交界处搜索得到较长距离的直线段，证明样条曲线能合理逼近非圆弧状滑动面。HHA对含软弱夹层边坡和多控制点的复杂滑动面搜索依然有效。

表4 考题答案对比

5 结论

(1)基于三次均匀B样条曲线构造边坡任意形状滑动面，探讨了曲线端点的处理方法与有效滑动面生成策略，有效地减少了优化变量，提高了搜索效率，保证了生成滑动面的形状自由与合理有效。

(2)将万有引力算法与粒子群算法相融合，并引入雁阵效应、非线性惯性权重进行改进，提出一种新的混合启发式搜索算法(HHA)，通过与其他算法进行对比，验证了HHA的优良性能。

(3)通过4道边坡稳定标准考题，分析验证了该文提出的样条滑动面和HHA搜索算法在边坡稳定分析应用中的可靠性与有效性，发现三次均匀B样条曲线能合理逼近任意形状临界滑动面；HHA对临界滑动面的搜索优于GSA，对非均质、含软弱夹层及地震作用下的复杂边坡均具有适用性。