江苏省物流业与制造业联动发展研究——基于耦合模型及灰色关联模型

林小芳

（南通理工学院商学院，江苏南通，226002）

物流业和制造业在国民经济发展总量中均占有重要份额，是两个关联度非常密切的产业，两者不可分割并相互影响、相互促进。两业的联动协调发展既关系到现代物流业的发展，又是促进制造业产业升级转型和提高物流企业核心竞争力的关键。物流业作为制造业稳定发展的驱动力，可以带动制造业经济效益的增长。随着劳动力成本的上升，制造业自身也亟需结构调整与转型升级，外包物流服务，提升专业核心竞争力。

物流业与制造业联动协调发展问题受到了各界人士不同程度的重视。早在2009年的《物流业调整和振兴规划》就将两业联动放在重要位置；2014年6月召开国务院常务会议，通过了《物流业发展中长期规划》（下文简称“规划”）。规划中提出了12项重点工程，包括“制造业物流与供应链管理”重点工程。规划同时指出，发展重点为“着力提升物流企业规模化、集约化水平”，“鼓励运输、仓储等传统物流企业向上下游延伸服务，推进物流业与其他产业互动融合、协同发展”。这说明了促进制造业与物流业联动协调发展的重要性。

江苏省作为一个制造业大省，其中苏南5市（镇江、南京、常州、无锡和苏州）成为“中国制造2025”试点示范城市群，发展制造业是省经济发展的重要推动力。如今制造业正在向产前、产后、分销和服务等领域转移，这一转型一定离不开物流业的支撑。因此，对江苏省物流业制造业联动发展进行研究具有一定的学术及实际意义。

一、文献回顾

国内外关于物流业与制造业联动发展的研究主要从联动内涵、机理、模式等方面展开，实证研究主要采用灰色关联、计量经济模型、投入产出等方法［1］。韦琦［2］运用向量自回归模型进行实证，并运用Granger因果检验分析两业的关系；朱长征［3］利用灰色关联法对陕西省两业联动发展进行定量研究；王珍珍［4］选取两业发展的七大指标，利用灰关联模型研究了我国不同综合经济区两业联动发展的关联度及协调度；董千里［5］根据两业联动三种基本模式类型设计联动发展水平评价指标，并根据FUZZY隶属度理论及模糊数学综合评判方法建立模型得出省域两业联动发展综合指数；宗刚等［6］利用灰色关联模型研究了长三角物流业制造业联动发展；靖学青［7］利用灰色综合关联分析研究了长江经济带两业联动发展；吴碧凡［8］利用Logistic模型对两业联动发展进行了动态均衡分析。

综上所述，现有研究多集中在利用各种单一模型进行物流业与制造业协同发展的理论研究，利用面板数据研究两业耦合协调发展并进一步分析两业发展指标间关系的研究不多；虽然有基于灰色模型的两业联动发展文献，但将耦合模型与灰色模型相结合，缺乏既测度两业耦合发展情况以及从细化指标细述两业联动发展具体原因的研究；目前研究中对江苏省两业联动发展的研究较少，研究方法过于单一。

因此，本文基于耦合模型、灰关联模型对江苏省物流业与制造业联动协调发展进行具体的定量研究，分析物流业与制造业两者评价指标间的关联度并得出结论。该结论不仅在方法上进行了一定的创新，得出的结论对于江苏省提升两业联动协调发展水平也有着重要的意义。

二、指标体系、数据来源和研究方法

（一）指标体系及数据来源

遵循科学性、可操作性和系统性原则，借鉴前人的评价指标体系，参考相关专家的建议，并考虑物流业与制造业两业之间的耦合发展关系，从经济性、规模性和效率性（表3）三个方面分别对两业进行评价。其中，物流业相关指标数据由交通运输、仓储与邮政业替代，物流业和制造业从业人数由法人单位从业人员替代。为了研究江苏省物流业与制造业的耦合协调性，取2000～2016年物流业与制造业的相关数据。除了文件中缺失的部分数据是依据已有数据推算得出，其他数据均取自江苏省统计年鉴及2017年中国物流年鉴。

（二）研究方法

1.数据的无量纲化处理

考虑到评价指标有正向指标、负向指标和适度指标不同的类型，需要首先将指标同趋势化，即指标的正向化处理；同时，为避免各评价指标单位的不一致而造成的误差，需要将数据序列转化为无量纲且数量级相同的序列。苏为华［9］将无量纲处理方法归纳为四类：广义指数法、广义线性功效系数法、非线性函数法和分段函数法。实际应用较多的有极差变换法、标准化法和均值化法。此处考虑到本文中各指标的特点，采用极大极小值法对原始数据进行处理，该线性变换方法不会改变数据的分布规律。公式如下：

正向指标：

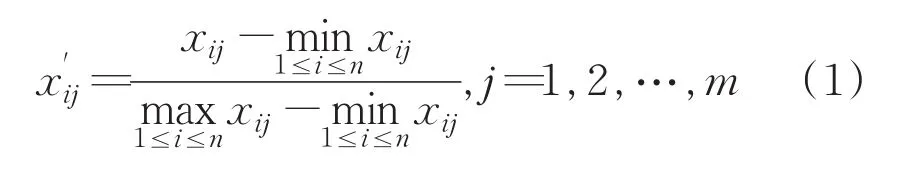
负向指标：

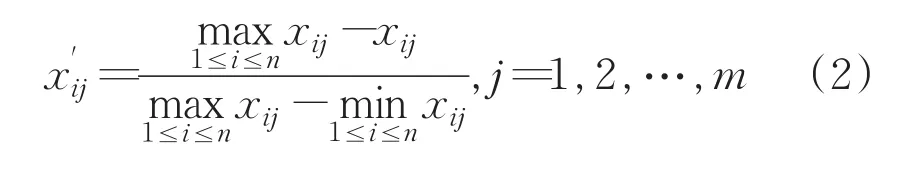
适度指标：

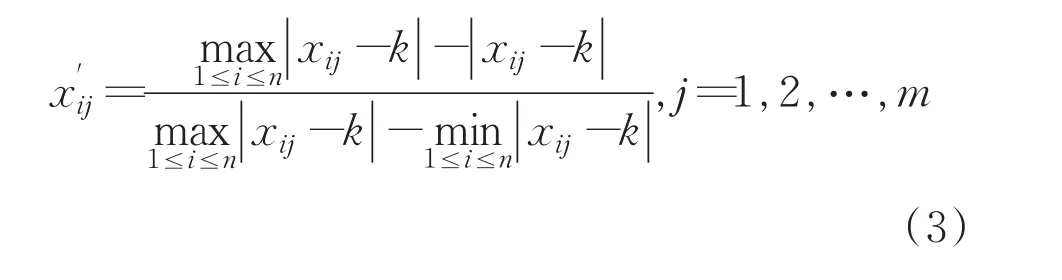
式中xij'表示第i年第j项指标的标准化指标；xij表示第i年第j项指标的原始数据。式（3）中k表示指标xij的理论最优值。

2.耦合模型

耦合是指多系统间相互作用、相互协调、相互促进、相互影响，最终联合起来形成一体化的现象，耦合度是对各系统之间协调关系和程度的度量。系统间联系越多，其耦合性越强，反之表明其耦合性越差。建立耦合模型计算耦合度，采用变异系数（离散系数）的评价函数来计算物流业和制造业的耦合度。变异系数反映两系统的变异或离散程度，其中对度量单位不同的几项指标的测量尤为适合。耦合度计算具体步骤如下：

（1）确定不同系统的综合发展评价指标体系，并确定各指标权重值。确定指标权重的方法一般有专家打分法、层次分析法、特征值法和熵权法等，为了避免评价指标权重确定的主观性带来的误差，可采用熵权法。该方法通过各指标之间的关联程度和相关信息来确定权重，能较客观地对评价指标权重进行确定。方法如下：

①原始数据的归一化处理

式中Pij是在第j项指标下第i个样本的比重。i表示样本号，j表示指标项，其中i=1，2，…，m;j=1，2，…，n。

②计算第j项指标的熵值

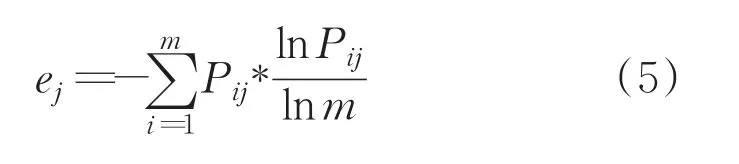
③计算第j项指标的权重

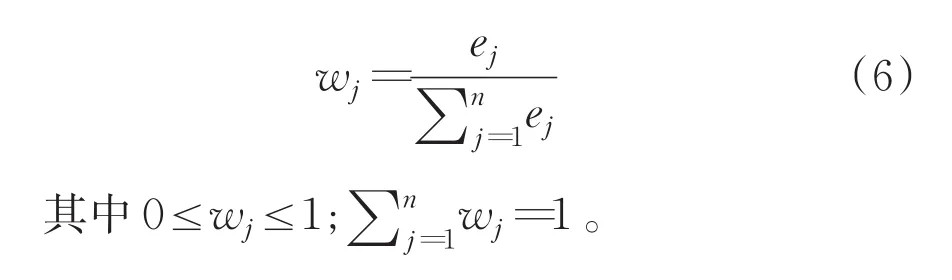
（2）根据各系统指标体系计算各系统的综合发展指数。Lx表示物流业综合发展指数；My表示制造业综合发展指数。

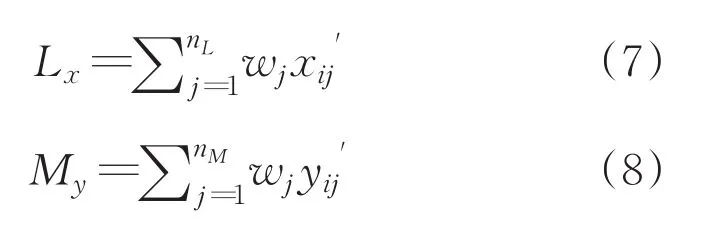
（3）计算两系统的协调度，公式为：

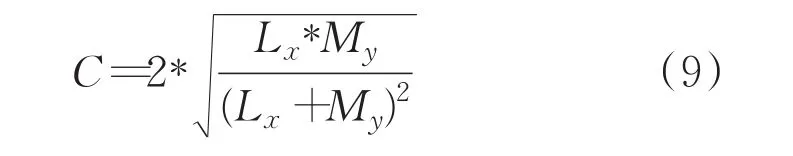
（4）计算两系统的发展度，采用公式：

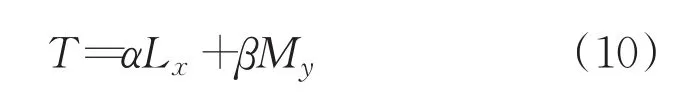
式中，α，β是待定系数，满足α+β=1。

（5）建立耦合模型并计算两业发展的系统耦合度，判别标准及类型如表1所示。

3.灰色关联模型

灰色系统理论由邓聚龙教授1982年创立，其灰色关联模型是根据数据序列曲线集合形状的相似程度来判断两者是否紧密相关，表现为曲线越接近，关联度越大。该方法能够弥补数理统计法对数据量和概率分布的要求，是近几年学者分析产业关联度的常用方法［10］。在两系统整体耦合分析基础上，通过灰色关联模型进一步确定两业各评价指标间的作用。具体步骤如下：

反应堆压力容器本体螺孔材质为16MND5，主要用于制作核电工程中蒸发器、稳压器、压力容器及封头、支撑部件。螺孔材质 16MnD5力学性能：HB=200，Rm=550-670Mpa，Rp0.2≥400Mpa；螺栓材料为 40NCDV7-0.3力学性能：Rp0.2≥900Mpa,Rm=1000-1170Mpa，HB=302-375。从力学性能来看，螺栓材质的硬度比法兰螺纹的硬度（相差约100HB），螺栓在下旋过程中形成积屑瘤产生高温并在螺纹之间产生塑性变形，使其硬度高于法兰螺孔材质的硬度，积屑瘤在螺栓与螺孔螺纹之间，随着螺栓的旋入在法兰螺纹螺牙上留下了沟痕，造成了螺纹损伤。

（1）根据研究需求确定参考序列与比较序列；

（3）计算两级最大差与最小差，M=

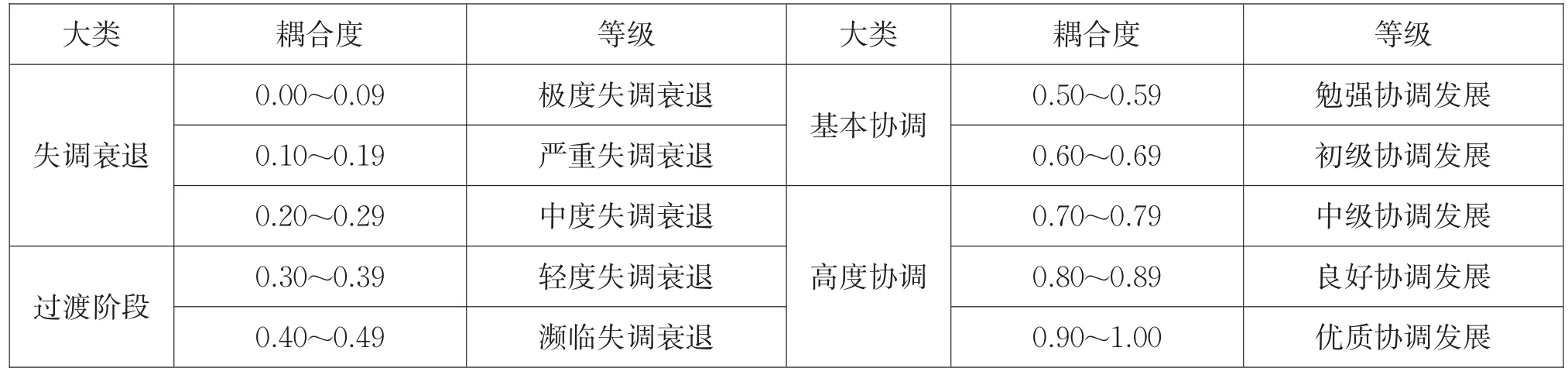
表1 系统耦合度判别标准及类型

表2 关联度界定标准

三、江苏省物流业与制造业耦合发展分析

（一）指标体系及指标权重的确定

数据分析采用了物流业3个一级指标，10个二级指标；制造业3个一级指标，11个二级指标，利用公式（1）—（6）确定各指标权重，如表3所示。

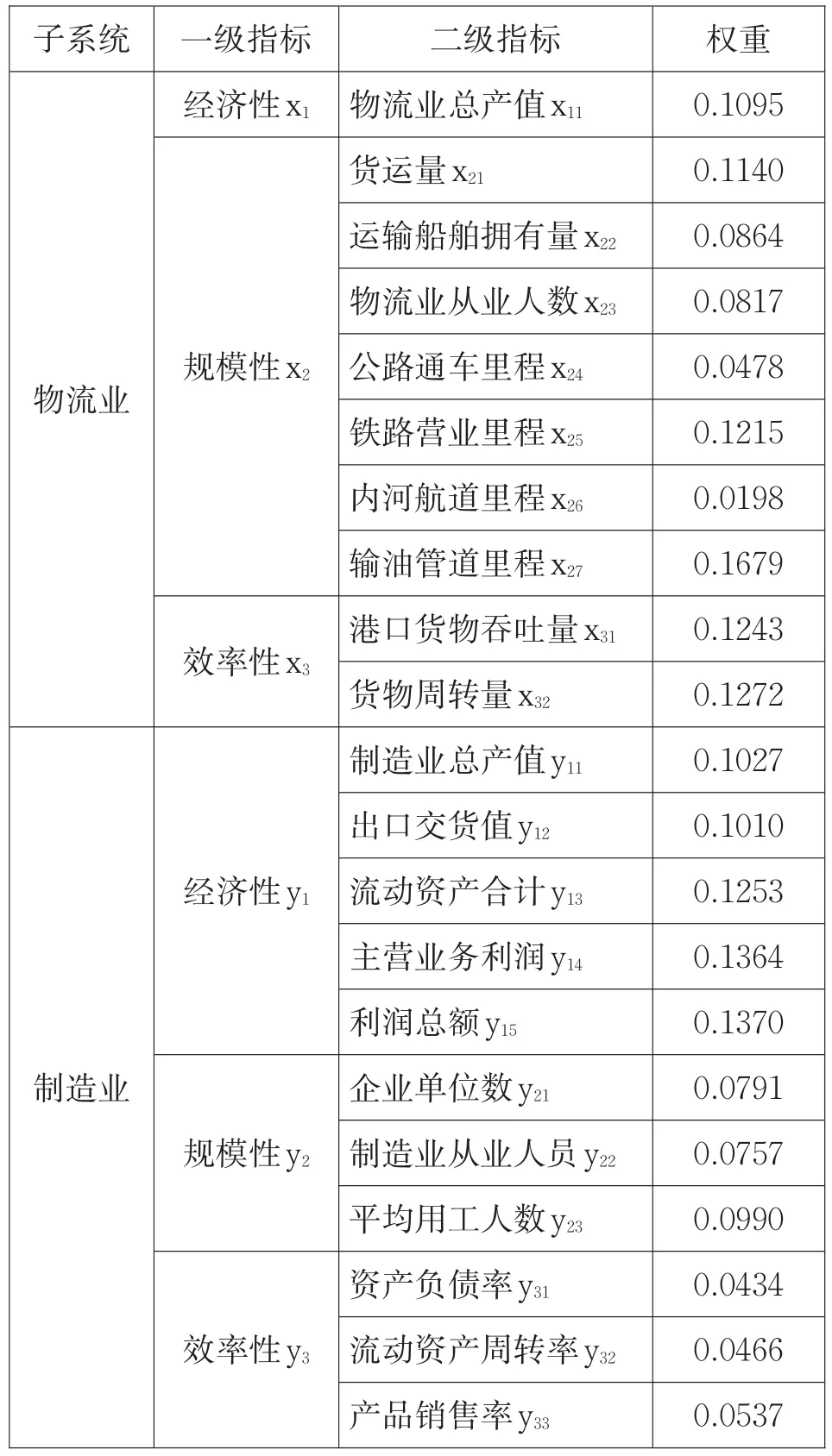
表3 物流业与制造业系统评价指标体系

以上共计21个细化指标中，制造业效率性指标“资产负债率”为适度指标［11］，其余指标均为正向指标。资产负债率理论最优值取0.5，采用公式（3）进行标准化处理。

（二）两业综合发展指数测算

利用公式（7）、（8）计算得到2000～2016年期间江苏省物流业和制造业的综合发展指数Lx、My，指数的变化情况如图1直观所示。通过对江苏省物流业与制造业综合发展指数的变化情况进行分析，得出以下结论：

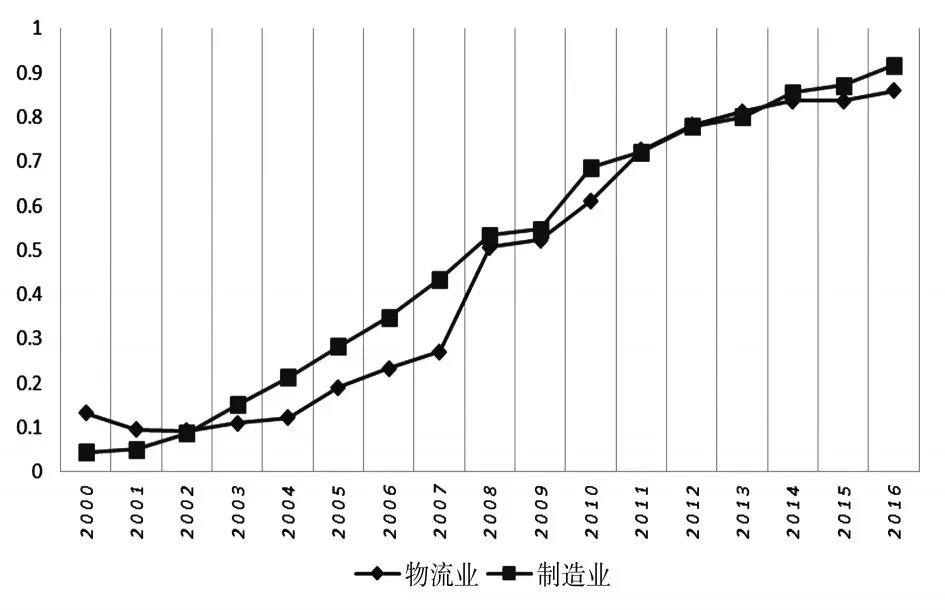
图1 江苏省2000～2016年物流业与制造业综合发展指数变化情况

1.2000 ～2016年期间，江苏省物流业与制造业综合指数整体上呈交错式上升趋势。这说明江苏省近几年物流业与制造业的发展一直处于快速上升阶段且制造业较物流业发展得更加快速。从图中可以看出，自2002年开始制造业呈直线上升式发展至2008年后稳步上升。物流业总体发展较为平缓，仅在2007～2008年间增长幅度较大。

2.从微观角度可知，在2000～2002年共3年期间，制造业与物流业相比，前者低于后者；2003～2010年共8年期间，有了较大改变，后者低于前者；2011～2013年期间，物流业综合指数略高于制造业综合指数；2014～2016年期间，制造业综合指数略高于物流业综合指数。

（三）江苏省物流业与制造业发展度及协调度测算

在分析江苏省物流业和制造业耦合发展情况时，借鉴逯进［12］等学者的耦合度模型，从发展和协调两个方面来研究。参考其他研究学者利用耦合模型确定待定系数的方法，在计算发展度时，假定物流业与制造业同等重要，确定待定系数均为0.5即α=β=0.5，这表明物流业与制造业两者一样重要。根据公式（9）—（11）分别计算江苏省2000～2016年两业发展度、协调度及耦合度（表4中所示）。

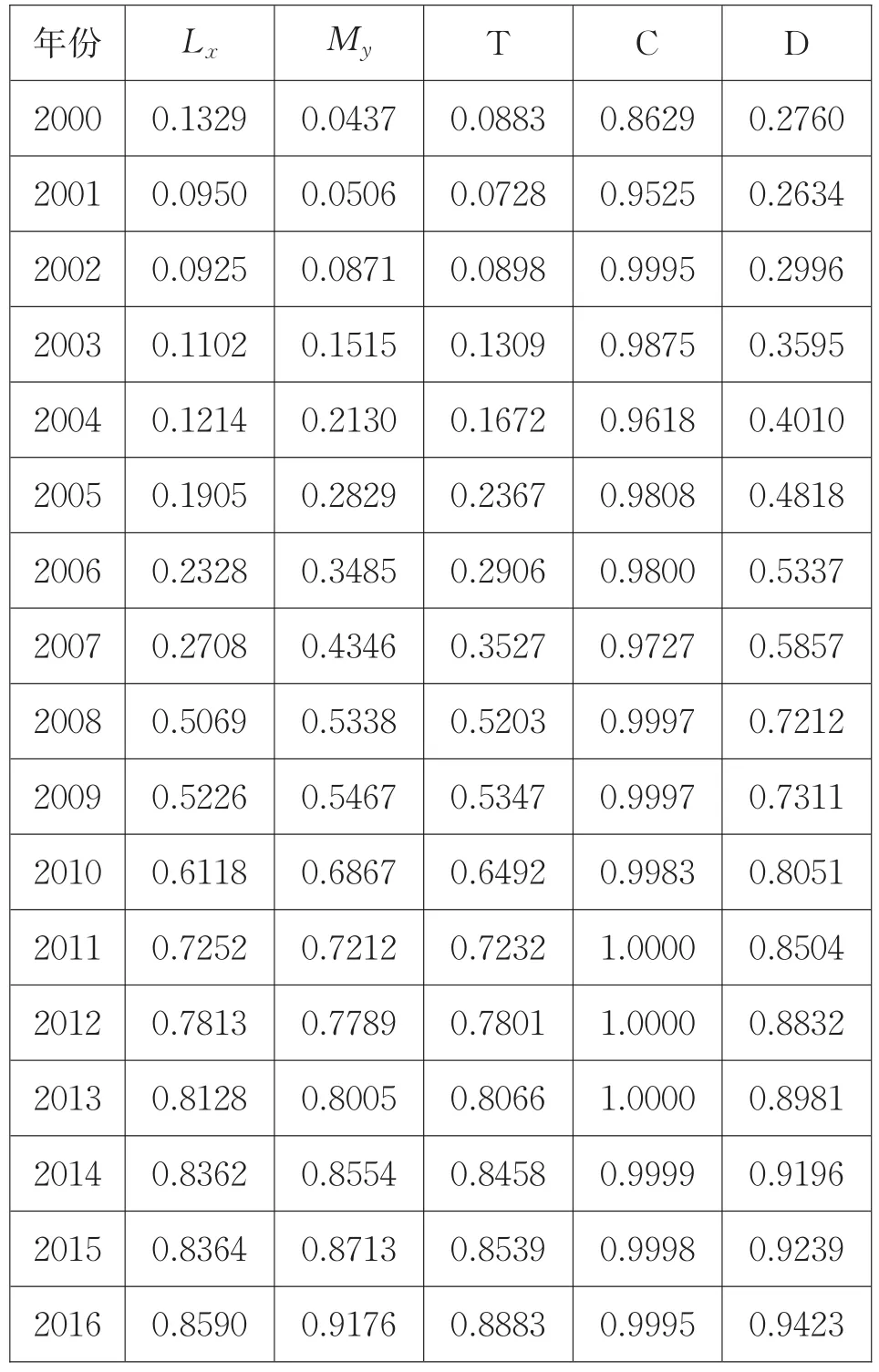
表4 2000-2016年江苏省两业综合指数及两业发展度T、协调度C、耦合度D

为了更直观地了解计算结果，以折线图的形式表现出来以便于更好的分析其在2000～2016年期间的变化情况，如图2所示。

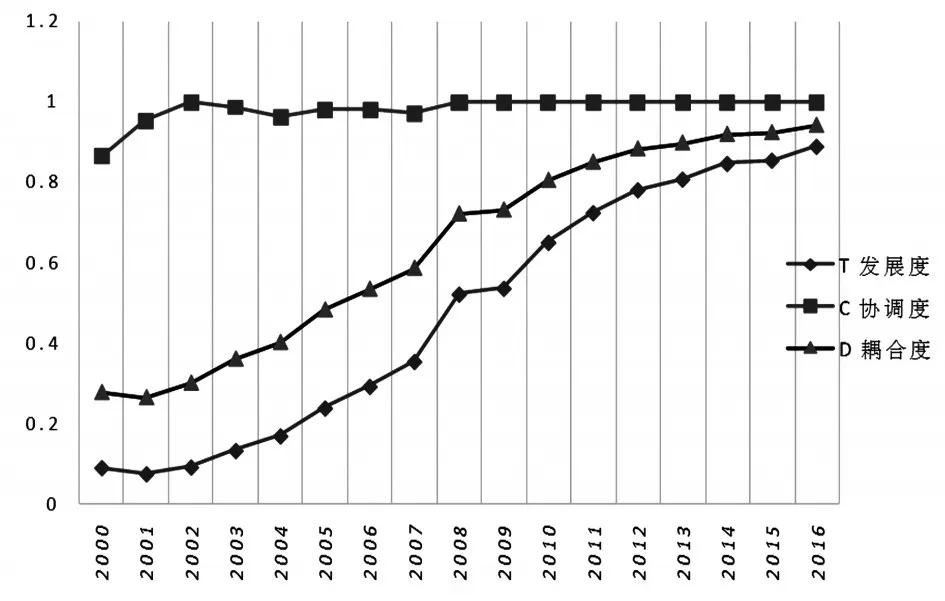
图2 江苏省2000-2016年物流业与制造业发展度、协调度及耦合度

（四）指数分析及结论

由表4及图2可直观看出，江苏省物流业与制造业总体上发展良好。特别是随着现代物流业的快速发展，制造业也随之出现相应的变化，与物流业的发展表现出更高的契合度，从二者在近年来的耦合度可窥见一斑：2000年两业耦合度为0.2760，2016年则为0.9423，为2000年的3倍多，改变与扭转了国家调控失控的局面。这表明江苏省近几年对物流业与制造业均十分关注，物流业与制造业两系统耦合度高，但是这种趋势不是长久保持的，会受到经济社会发展因素的影响。

根据对数据结果的分析，江苏省物流业与制造业结合发展会使江苏省整体水平大大提高，从而带动江苏省的经济发展，使江苏省经济发展水平位居全国前列。此外，江苏省物流业与制造业高度的耦合协调发展也给我国其他省市树立了榜样，起到了模范带头作用。

四、江苏省物流业与制造业灰色关联度分析

为进一步分析物流业各指标与制造业各指标之间的关联度，选取2000～2016共17年21个指标值（同协整分析部分），采用灰色关联模型进行数据的进一步分析。

（一）数据分析

经标准化后的数据序列，确定参考序列和比较序列。将物流业各指标的时间序列观测值作为参考序列，制造业各指标的时间序列观测值作为比较序列，分别计算物流业10个二级指标和制造业11个二级指标的灰色关联度，如表5所示。

（二）结果讨论

从两业指标灰色关联度数据看：江苏省制造业各指标与物流业指标平均灰色关联度在0.596～0.754之间，属于适中关联的指标仅有企业单位数y21，其余均为较强关联，说明江苏省制造业各指标对物流业的发展影响均较大。其中，制造业发展对物流业主要制约因素为发展规模中的平均用工人数y23（关联度0.754）、经济性指标中的制造业总产值 y11（关联度 0.753）、主营业务利润 y14（关联度0.747）。另一方面，制造业企业单位数y21（关联度0.596）与物流业的关联度最小，表明制造业对物流业的作用不单纯体现在企业个体数量的多少，而在于整体发展规模。

若用公路通车里程x24作为江苏省物流业发展参考序列，制造业指标中与其关联度由高到低分别是 y23>y11>y31>y14>y32>y12>y33>y15>y22>y13>y21，这表明江苏省制造业中的规模性指标“平均用工人数”、经济性指标“制造业生产总值”与物流业发展关联性较大。其中，“制造业生产总值”指标与多数学者的研究结论一致。

物流业指标中与制造业各指标平均关联度较大的前两个指标分别是公路通车里程x24（关联度0.771）和物流业总产值x11（关联度0.748）；运输方式中，除铁路营业里程x25（关联度0.675）关联度偏低外，公路通车里程x24（关联度0.771）、内河航道里程x26（关联度0.743）两个规模性指标与制造业关联度较高。这表明公路运输方式在产品的运输过程中应用较为广泛，而江苏由于多沿海城市，水上运输对制造业物流也起到较强的推动作用。除此之外，物流业从业人员数也是一个关键指标，因为这在一定程度上反映了物流业对货物运输供给能力的大小，对产品配送具有一定的影响。

五、结论与建议

基于耦合理论和灰色关联模型，对江苏省物流业与制造业两业联动协调发展情况进行数据分析。主要研究结论有：（1）近几年来江苏省物流业与制造业一直处于交错快速上升的趋势，且耦合度逐年递增；（2）从细化指标的关联度来看，江苏省制造业各指标与物流业发展的关联度较大，基本属于较强关联的水平，制造业整体发展水平对物流业有着重要的拉动作用；（3）物流业指标中不同运输方式与制造业关联度较大，特别体现在公路与水上运输方式。

针对以上结论，给出江苏省制造业与物流业联动发展的建议：

第一，制造业是江苏省经济发展的动力和支柱，占据着重要地位，物流业是经济发展的基础和动脉，二者相互渗透、相互融合，达到联动发展双赢的效果。在某种程度上而言，物流业的发展决定了制造业能否获得长足发展。因此，必须在结合现行发展的基础上，重视二者之间的相互协调发展，打造二者在现代社会发展下的新型协同模式，调整当前产业利益格局，为现代经济社会发展作出新的贡献。为了江苏省物流业与制造业耦合协调发展，政府方面应着力构建两业耦合发展的良好环境，大力发展物流业，推进物流专业化发展。

第二，物流业是在工业制造业发展过程中不断衍生分离出来的，制造业是社会物流行业服务的主要对象，因此制造业决定了物流业的发展方向，物流业的发展重点与项目都要以制造业的实际需求为导向，在此过程中不断探索发展合作新模式，提高合作效率，达成共赢。

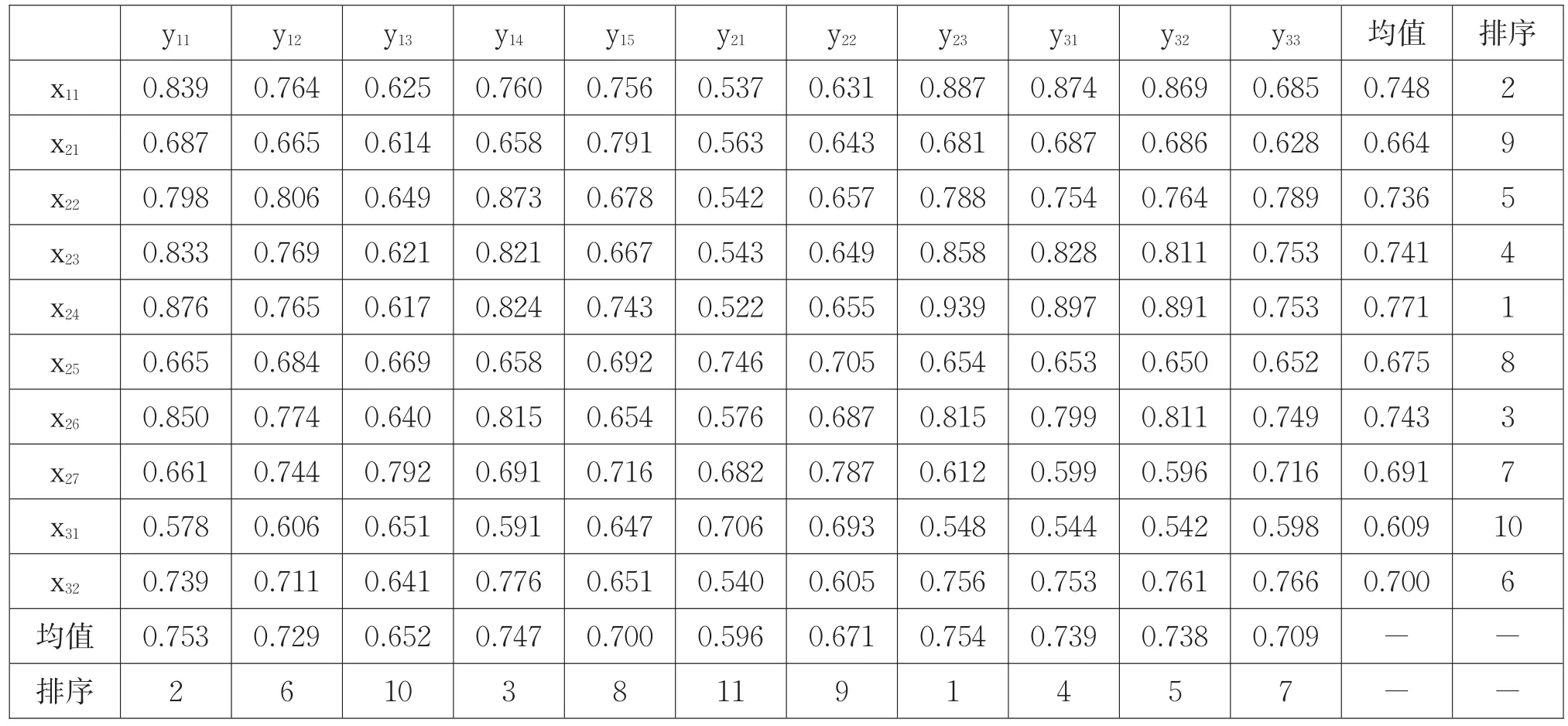
表5 江苏省物流业与制造业各评价指标灰色关联度

第三，充分利用江苏省沿海城市的特点，加强建立多种运输方式转换途径，衔接海陆空运输方式，加大港口、码头等物流基础设施的建设完善力度，更好地推动江苏省制造业的协同发展。