井中充电法三维数值模拟研究

尤 淼，穆海棠，张金会

（安徽省勘查技术院，安徽 合肥 230031）

充电法（“Mise-a-la-Masse”method）是通过将良导体直接连通电源，观测其电场分布特征和规律进行找矿勘探的—种方法。在理论研究方面，何裕盛等[1](1978)对充电法的方法原理进行了系统研究；王志刚、何展翔等[2]（2006），使用有限差分法进行井地电法三维数值模拟并研究异常规律。基于前人的研究基础，为进一步了解点源和异常体位置的不同组合对地表电场分布的影响，本文使用有限单元进行数值模拟研究。

1 点电流源有限单元法数值模拟

将点电流源置于水平地面，如图所示：

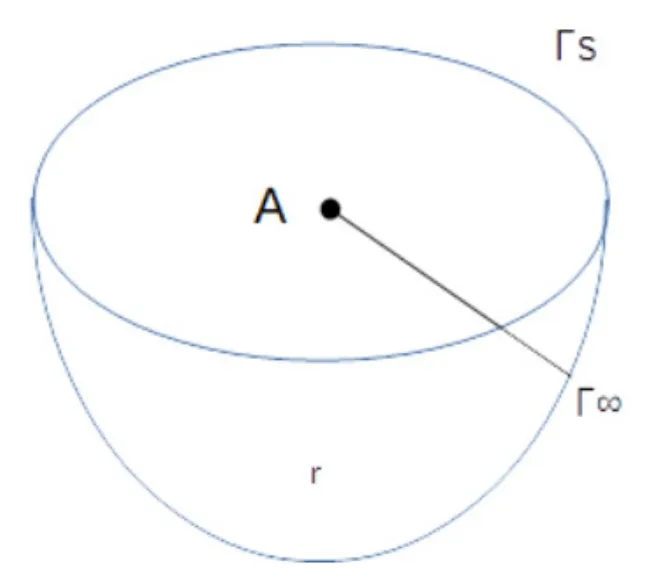
图1 三维点源示意图

根据文献[3]，三维地电结构下电源电场总场的边值问题为：

三维总场电位法的边值问题对应的变分问题为：

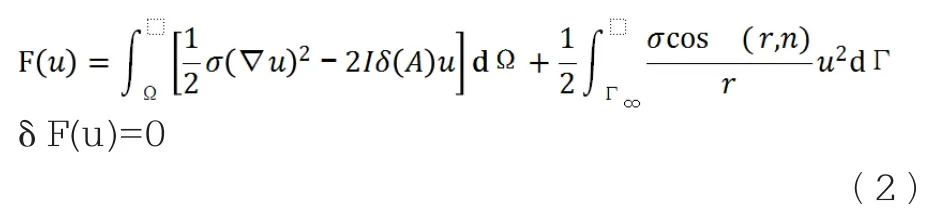
研究区域为如上图所示的地下三维空间，采用六面体单元进行剖分、三线性插值表示单元内部任意位置的电位值。

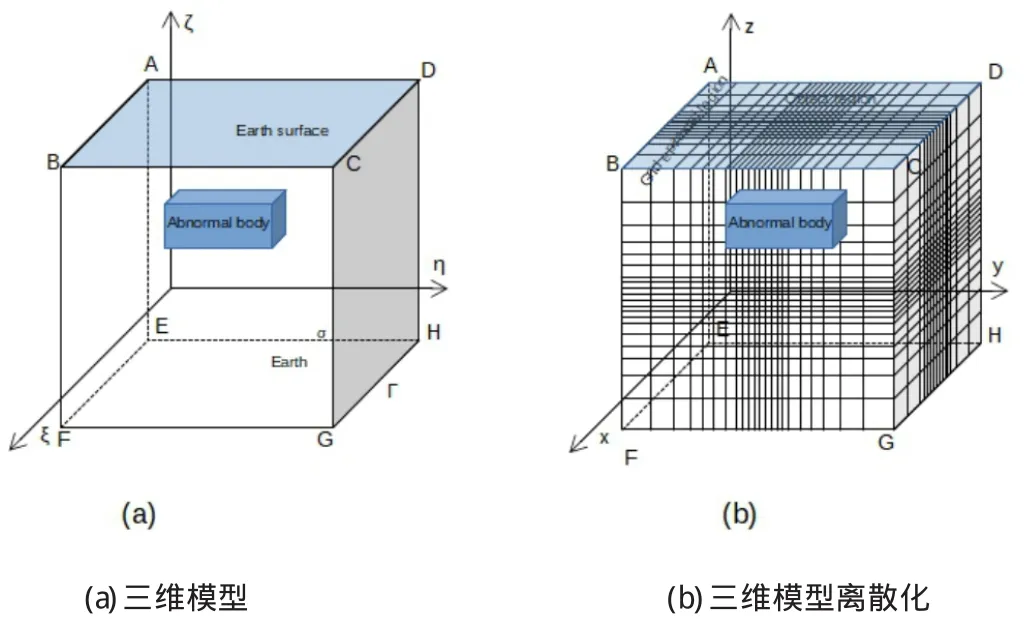
图2 三维模型及离散化示意图

使用以上网格将变分问题离散化，最后得到一个线性方程组：

求解该方程组，即可获得各节点的u。

2 数值模拟结果

基于有限单元法公式推导，编写相关程序。设计几个地电模型，进行数值模拟计算，将模拟结果分别绘制成地表电场分布和梯度矢量图。

2.1 模型1

解析解对比，为验证点源三维数值模拟的正确性，使用两层模型解析解结果进行验证。该模型为一个两层G型地电模型，第一层厚度2m，电阻率1Ω·m；第二层为一均匀版空间，电阻率19Ω·m。网格设置为，水平方向（X方向）上41个测点，Y方向上41条测线，在21号测线的21号测点上供电，在21号测线的其他测点上测量电位，X方向上电极距1m，Y方向上测线之间的距离为1m，取供电点为坐标原点，X方向，远边界为296m，Y方向上，远边界为261m，Z方向上共15个网格，下边界为-266m。采用三维有限单元法模拟的结果与理论值对比如表1所示：

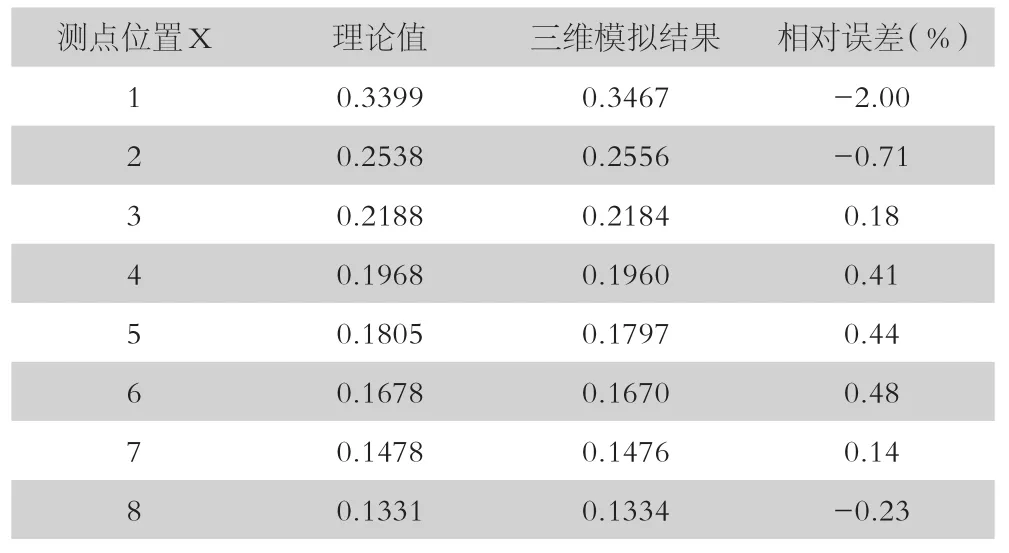
表1 三维总场法数值模拟结果

从模拟结果可以看到，在距离电源点最近的测点上，模拟结果与解析的误差最大，达到2%，但是随着测点远离电源点，误差逐渐变小，可满足数值模拟需要的精度。

2.2 模型2

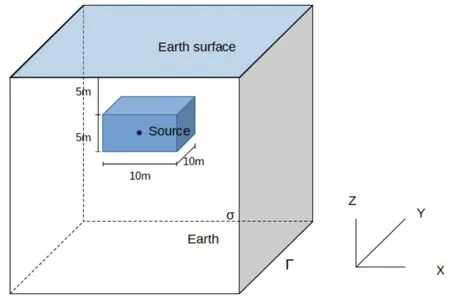
图3 模型参数设置

模型2为一个1000m×1000m×1000m的三维地下空间，研究区域中间加密部分的网格规模为40×40×40，x、y、z正负方向各向外部扩展20个网格。模型背景电阻率为100Ω·m，异常体位于模型中间，电阻率大小10Ω·m，异常体大小为10m×10m×5m，异常体顶部深度5m。

点源位于异常体中心位置。使用三维正演模拟计算该模型的地表电位分布信息，电位分布和电位梯度矢量如图4所示，图中灰色区域为异常体在地表的投影部分，黑色三角形为供电点源在地表的投影位置，背景部分为地表电位等值线，黑色箭头为地表电位梯度。

可以看到，电位等值线由点源位置向各方向均匀扩展，电位值逐渐降低，由梯度矢量图也能明显观察到电位由中心向外扩散的分布趋势。

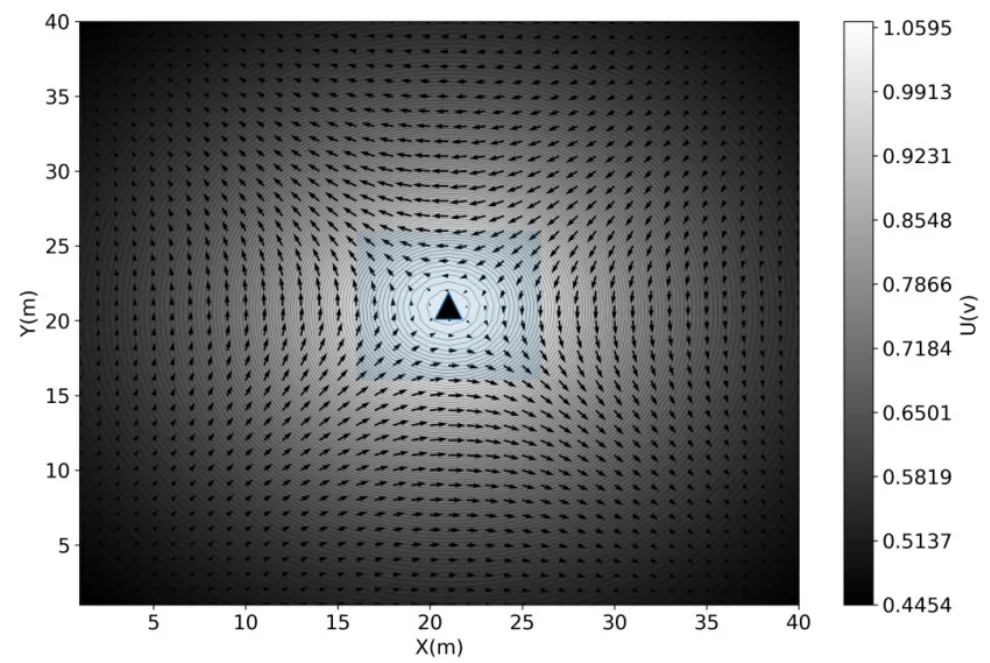
图4 地表电位分布和梯度矢量图

2.3 模型3

模型3为一个倾斜板状异常体模型，异常体位于一个1000m×1000m×1000m的三维地下空间内，研究区域中间加密部分的网格规模为40×40×40，x、y、z正负方向各向外部扩展20个网格。

模型背景电阻率为100Ω·m，异常体位于模型中间，电阻率大小10Ω·m，异常体横向长度10m，横向宽度10m，垂直厚度10m，顶部深度5m。

图5 模型参数设置

供电点位于异常体中心位置。使用三维正演模拟计算该模型的地表电位分布信息，电位分布图和梯度图如图6所示。

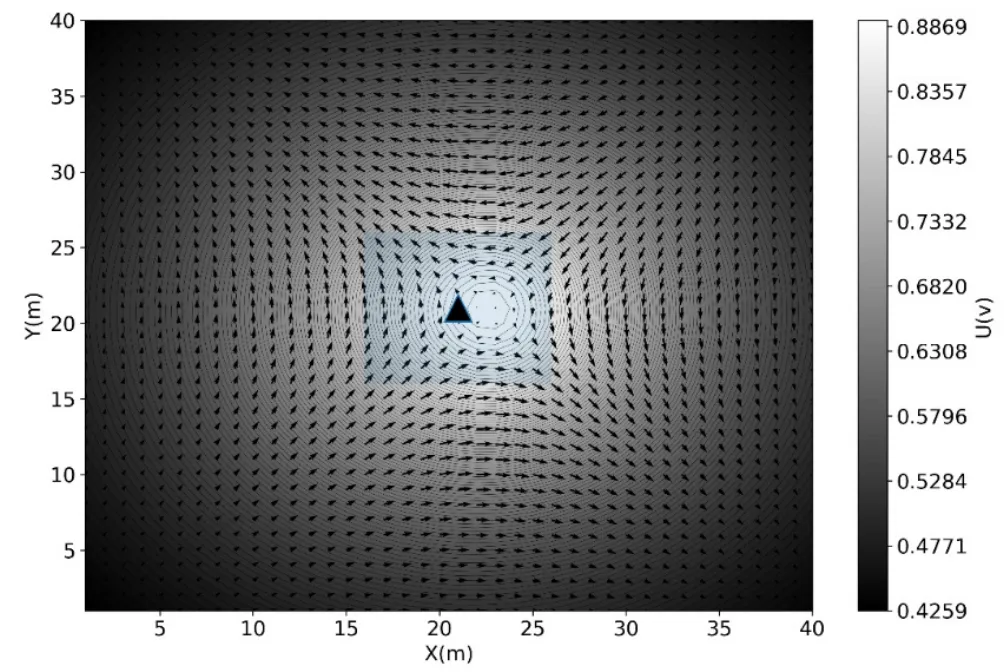
图6 地表电位分布和梯度矢量图

由地表电位分布可以看到，倾斜板状体影响下，地表的等值线图左右分布趋势并不一致，表现为右侧为高电位分布，梯度矢量图的中间高值部位与供电中心有明显偏移，反映了深部倾斜状异常体的影响。

3 结论

充电法正演模拟结果表明，通过地表电位分布、电位梯度和电位梯度矢量数据，可以对地下矿体的规模和位置进行较准确的判断。

充电法作为一种施工简易、成本低的物探方法，在已有钻孔的工区周边寻找更多的未知矿脉和扩大找矿范围工作中有着良好的应用前景。

下一步工作为进行更多的模型实验，为野外数据采集工作提供理论保障，并验证该方法在覆盖区、起伏地形等复杂条件下的实际效果。