基于气动弹性的风力机叶片气动与结构性能研究★
朱 杰
(嘉兴学院建筑工程学院,浙江 嘉兴 314001)
0 引言
传统方法在设计叶片时将其视作刚性,不考虑弹性变形对载荷及其性能的耦合影响[1]。随着风力机向大型化、轻量化发展,叶片柔性不断增大,忽略气动弹性效应将使其性能偏离原设计值,甚至产生破坏[2]。因此,研究气动弹性问题对大型叶片的设计具有重要意义。
许多学者已展开了相关研究工作[1-6],但侧重点大多偏向于气动性能分析,鲜有同时对结构性能进行研究的报道。本文提出一种基于动量叶素理论与有限元法相结合的方法,对某1.5 MW叶片进行考虑气动弹性效应的气动与结构性能研究。
1 叶片气动与结构性能计算模型
1.1 叶片气动性能计算模型
采用动量叶素理论计算载荷与叶片气动性能。作用在长度为dr的叶素上的气动力如图1所示。各气动力表达式如下:
(1)
(2)
(3)
(4)
式中:dL——升力;
dD——阻力;
dpN——推力;
dpT——切向力;
ρ——空气密度;
W——入流相对速度;
c——弦长;
Cl——升力系数;
Cd——阻力系数;
φ——入流角,由桨距角θ、攻角α和变形扭角φ三部分组成。
风能利用系数CP和年发电量AEP计算公式为:
(5)
(6)
式中:P——输出功率;
v——来流风速;
A——风轮扫风面积;
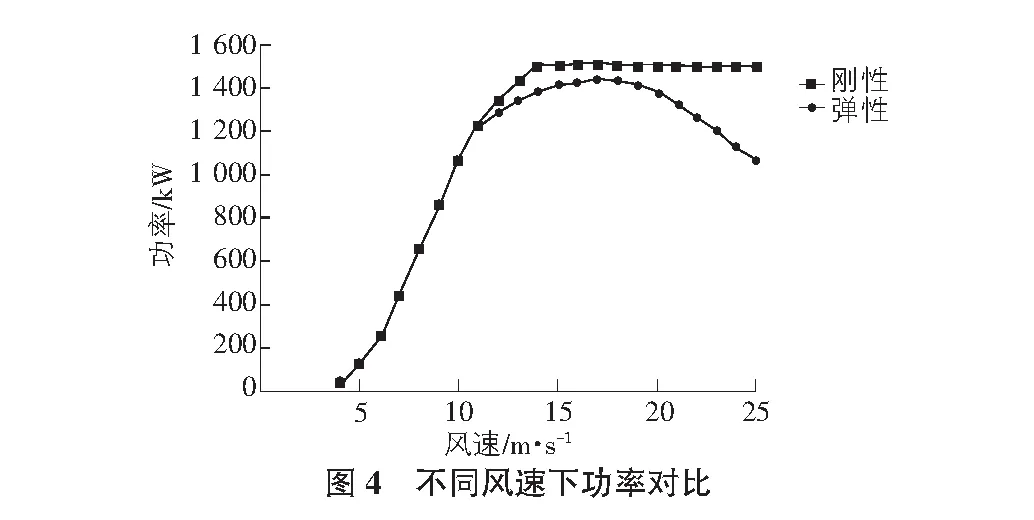
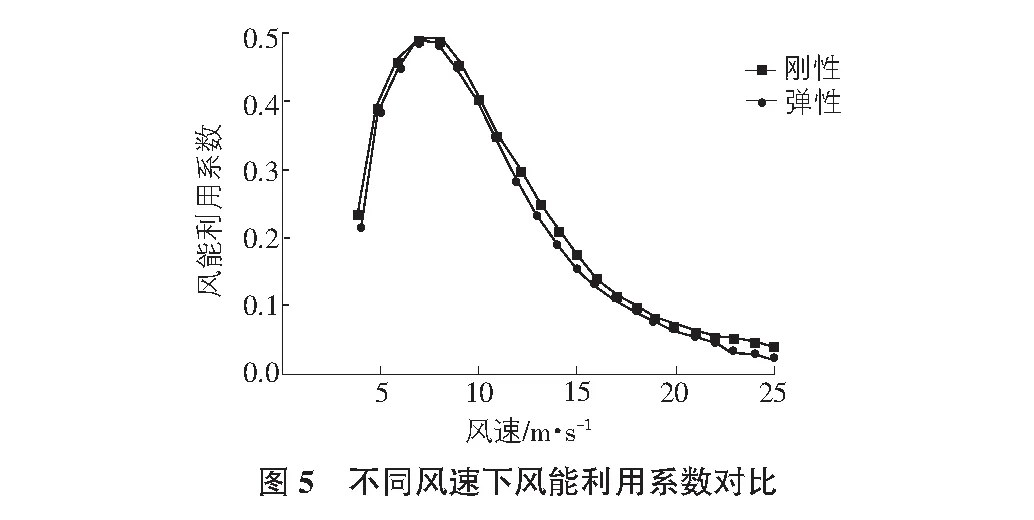
f(vi 图2为叶片典型剖面结构形式,可分为主梁、腹板、前缘与后缘四部分。主梁主要由单向玻璃纤维层合板组成,腹板、前缘和后缘由玻璃纤维织物与夹芯材料构成。 采用有限元法在ANSYS中建立叶片结构性能计算模型,分别利用Shell99和Shell91壳体单元对主梁铺层和其他部分夹层结构进行模拟,有限元模型如图3所示。 本文所研究的1.5 MW叶片长37 m,切入风速为4 m/s,切出风速为25 m/s,额定风速为14 m/s,额定转速为16 rpm,风速分布模型采用平均风速为6 m/s的Weibull概率分布。 气动弹性耦合计算过程如下:首先采用动量叶素理论求得叶片在运行工况内各风速下的初始气动载荷,将其施加于有限元模型上进行叶片变形计算以获得变形扭角;然后根据变形扭角更新入流角,重新计算气动载荷进行新一轮迭代;如此循环直到叶尖变形满足收敛条件停止计算。 图4与图5分别为考虑气动弹性前后不同风速下的功率和风能利用系数对比图。可以看到,在运行工况内,气动弹性对两者都存在一定的负面影响,即会降低功率和风能利用系数。随着风速的增大,该负面影响呈现出先增大、后减小、再增大的趋势。其中,在4 m/s~10 m/s较低风速范围内,气动弹性对功率和风能利用系数的影响较小,可不予考虑;当风速大于10 m/s后,由于叶片变形的增大导致气动弹性对功率和风能利用系数产生显著影响,甚至无法使功率达到额定值。 考虑气动弹性前后的年发电量分别为3.439 Gwh/yr和3.377 Gwh/yr,两者差别不大。这是因为本文所研究的叶片在较低风速区域有较好的气动性能,尤其在6 m/s~9 m/s风速范围内的风能利用系数均超过0.4。尽管气动弹性对高风速下的气动性能影响显著,但对于全年平均风速为6 m/s的风场而言,高风速下的概率密度很小,故而其对年发电量的影响也较小。 图6与图7分别为考虑气动弹性前后不同风速下的最大叶尖位移与叶片最大等效应变对比图。由图6可见,考虑气动弹性可减小最大叶尖位移,且随着风速的增大,减小量逐渐增大。由图7可知,考虑气动弹性时,在4 m/s~7 m/s风速范围内,叶片最大等效应变有所减小;当风速超过7 m/s后,叶片最大等效应变有所增加,且随着风速的增大,增量逐渐变大。产生上述现象的原因在于考虑气动弹性时,作用在叶片上的推力逐渐减小,而切向力则是在4 m/s~7 m/s风速范围内有所减小,随后逐渐增大。通过对比可以发现,叶尖最大位移主要取决于推力,最大减小量为50 mm,仅为对应最大叶尖位移值的1.76%,表明气动弹性对叶尖位移影响较小;叶片最大等效应变则更多取决于切向力,最大增量为150.4,是对应最大等效应变值的5.44%,表明气动弹性对等效应变影响相对较大。 通过对某1.5 MW风力机叶片进行基于气动弹性的气动与结构性能研究,可得如下结论:气动弹性对叶片气动性能有负面影响,随着风速的增大,该负面影响先增大、后减小、再增大;气动弹性对最大叶尖位移有较小的正面影响,对叶片最大等效应变则更多地存在相对较大的负面影响;本文提出的方法可较为准确的分析气动弹性对叶片气动与结构性能的影响,应用该方法能对叶片设计进行有效修正,并可为后续基于气动弹性的叶片优化设计奠定基础。1.2 叶片结构性能计算模型


2 计算结果及分析


3 结语

