基于改进GM(1,1)预测模型的铁路客运量预测★

陈会如 逯兆友 刘孝辉 李洪涛 侯玉宁 李浩雅

(1.东北林业大学交通学院,黑龙江 哈尔滨 150040； 2.东北林业大学信息与计算机工程学院，黑龙江 哈尔滨 150040； 3.东北林业大学机电工程学院，黑龙江 哈尔滨 150040)

1 概述

客运量的预测服务于旅客运输中车辆调度及线路规划。准确的预测有利于轨道交通营运路线及车辆数目的规划，为国家对市场出租车保有量的宏观调控提供数据依据。使居民出行更加方便、舒适，减少因车辆配置不合理而出现的各种运输不合理现象，造成物质、时间资源的浪费。在长途运输方面，除了对车辆数目和线路的规划外，准确的客运量预测对运输结构的规划管理起到了数据支撑的作用，运输经营者可以通过预测客运量对运输结构进行调整，以便适应不同旅客的不同运输需求[1-3]。因此，保证客运量预测的准确度至关重要。

预测模型的选择则是保证客运量预测准确性的前提。目前，在客运量的预测上通常选用灰色预测模型，如桂文毅等人运用灰色线性回归模型对哈尔滨铁路枢纽客运量进行预测，预测评价检验结果为优，预测结果可靠[4]。灰色预测模型的应用很广，在工程领域内对某些数据随时间变化的序列进行预测，从而做出更精准的调节和建设。如郑旭东等人将灰色预测模型应用于大坝的实际水平径向位移预测中[5]；陈朝锋等人运用改进的灰色预测模型对中长期煤矿电力系统负荷进行预测[6]；此外国内外学者还将灰色预测模型应用于风电功率预测[7，8]。

但是，灰色预测模型在某些情况下精度会下降，需对其进行改进以提高其估测精度。如：付建飞等人在针对铁路分品类货运量预测时，发现对数据序列波动性大的品类预测运用灰色预测模型效果一般，采用指数平滑法对灰色预测的结果进行修正，提高了总体预测效果[9]。王渊等人提出改进的GM(1,N)非线性优化方法,并将其应用于邯郸市2010年—2015年地下水矿化度的拟合预测中，结果表明改进的非线性GM(1,N)模型拟合精度较好[10]。

本文将利用遗传算法对灰色预测模型中的参数计算进行优化，以期提高预测精确度。

2 预测模型

2.1 GM(1,1)预测模型

灰色预测是根据系统内各因素之间的不同变化状态，通过关联性分析，找到系统变化发展的趋势，生成具有一定规律性的预测数据序列，再通过建立相关微分方程模型，对未来数据进行分析预测，得到相应数据序列的预测序列[4]。在进行灰色预测时，要进行灰色量白化的过程，使看似杂乱的数据序列表现出一定的规律性，从而建立模型得出预测结果。白化过程如下：

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(1)

式(1)为原始的随时间变化的数据序列，通过对原始数据的直观观察可以看出客运量的总体变化趋势是递增的，但是规律性不强，因此在进行灰色预测前要对数据序列进行灰生成。

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(2)

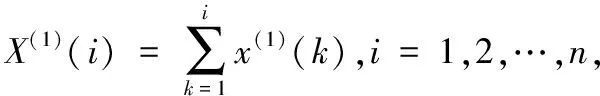
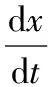
(3)

该方程的解为:

x(1)(k+1)=[x(0)(1)-b/a]e-ak+b/a

(4)

在GM(1,1)模型中，当发展系数a为负时，系统的变化速度与其绝对值正相关；当a为正时则呈现负相关。内生灰作用量b反映了数据变化的关系。对参数a和参数b的求解是灰色预测的关键，传统的灰色预测模型求解这两个参数时使用的是最小二乘法(下文将对这部分进行优化)，其原理如下：

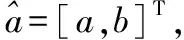
(5)

Y=[x(0)(2),x(0)(3),…,x(0)(n)]T,在python3.6中进行编程，运行得到a=-0.052 8，b=2.446 5。

将a，b代入式(6)：

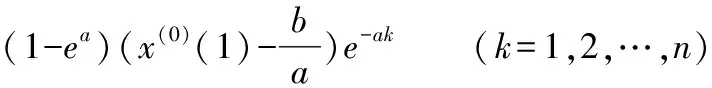
(6)

当后验差比值大于0.35或者准确度小于0.95时，灰色预测不适用。

2.2 基于遗传算法的改进GM(1,1)预测模型

传统的灰色预测求解参数a和参数b的方法是最小二乘法，但是当矩阵接近退化时，最小二乘法的精确度降低，使得预测值误差增大。因此，优化GM(1，1)模型求参数a和参数b的过程，有利于提高预测准确度。本文采用遗传算法取代最小二乘法来对模型进行优化。

首先，随机产生参数的初始种群，初始种群的范围对算法的效率影响很大，因此要使种群的范围更加精确，提高计算速度。通过最小二乘法计算确定初始参数值a0,b0，种群的范围应包含初始解且其边界在初始解附近，则令a∈(0.8a0,1.2a0)，b∈(0.8b0,1.2b0)。

在参数a和参数b的种群中，评价其适应度的目标函数为种群中每个个体所求预测值的精度累加之和，目标函数越小则适应度越大，函数如下：

(7)

在程序运行的过程中，遗传算法每一次迭代得到的种群个体都要代入灰色预测中进行计算，将计算结果与真实值进行精确度分析，在编写代码时适应度函数要调用整个灰色预测函数，将种群个体传入其中，省略了每一步中灰色模型的最小二乘法计算的过程。

2.3 模型精度评价

与其他预测模型相比，GM(1,1)模型所需的样本数量小，数据的分布不需要有规律性。数据按照时间序列排列，易于预测未来中长期的数据，精度高的同时，定量分析的预测结果和定性分析的结果一致[11]。铁路客运量数据类型与GM(1,1)模型所需数据类型一致，因此在进行预测时选择GM(1,1)模型得到的预测结果精度较高。

3 客运量预测结果与分析

3.1 基于GM(1,1)模型预测结果

本文中对应的是1990年—2017年的全国铁路客运量(数据源自中华人民共和国国家统计局《中国统计年鉴》)如表1所示。

表1 原始数据序列

选取1990年—2012年的客运量作为训练集，2013年—2017年的客运量作为测试集。基于GM(1,1)模型预测结果如表2所示。

后验比C=0.213，但是准确率P=0.870，此时灰色预测在预测时表现得并不理想。

3.2 基于改进GM(1,1)模型预测结果

种群个体采用二进制编码，用随机遍历抽样的方式进行个体选择，以默认概率Pc=0.8进行单点交叉，变异概率为Pm=0.01，最大迭代次数设置为10 000。优化过程如图1所示。

表2 灰色预测结果

得到参数a和参数b的收敛情况如图2所示。

得到的最优参数值为a=-0.041，b=84 243.205。得到解的情况如表3所示。

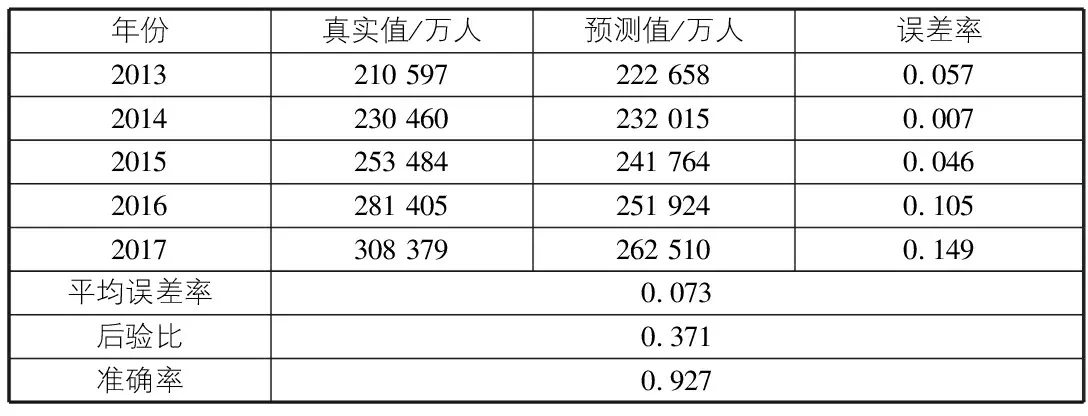
表3 改进后的预测结果

4 结语

本文通过遗传算法来改进传统GM(1,1)预测模型中计算发展系数和内生灰作用量的最小二乘法，以提高预测精度，所得主要结论如下：

利用遗传算法对GM(1,1)预测模型进行优化能够提高铁路客运量预测模型精度。通过GM(1,1)预测模型进行预测得到的预测结果与真实结果的平均误差率为0.259。利用遗传算法对GM(1,1)预测模型进行优化，使得模型预测结果平均误差率为0.073。相对而言平均误差率减小了0.186。