L2损失大规模线性非平行支持向量顺序回归模型

石勇 李佩佳 汪华东

顺序回归旨在对具有顺序标签结构的样本进行分类.近些年随着数据挖掘和机器学习技术的发展,顺序回归模型在情感分析、产品评论、信用评估、用户画像等领域得到了广泛应用[1−3].在这些领域中,其样本标签包含顺序信息,不同的错误样本代价往往不同.如用户画像领域中对年龄的预估,20岁的青年用户被错分为30岁和50岁形成的用户画像有明显差异.再如在信用评估领域,一个信用值极低的公司被错分为一般低和较高所影响的决策大相径庭.因此,顺序回归问题受到越来越多的重视.顺序回归在机器学习领域中介于分类问题和回归问题之间.与分类问题不同,顺序回归问题的标签集合具有顺序结构而不仅仅是一个多类别集合.再者,与回归问题不同,顺序回归问题的标签不具有度量信息.

在解决顺序回归问题时一方面需要考虑顺序信息,另一方面由于对不同分错样本的处理不同,所以在构建模型时,对损失项的特殊处理有助于使预测标签与实际标签尽可能接近,提高模型的性能.如此,为了使与真实标签产生较大偏差的样本得到更大的惩罚,我们在建模中采用L2损失(均方Hinge损失)作为模型损失函数,旨在最小化真实值与估计值的距离的平方,使得训练的模型能更好地处理与真实标签间的差异.与此同时,L2损失对离群点较敏感,一个合适的训练模型算法显得如此重要.针对求解算法,Hsieh等研究了标准的线性支持向量分类(Support vector classification,SVC)[11]和支持向量回归(Support vector regression,SVR)[12]求解算法,并提出了相应处理大规模数据的求解算法如对偶坐标下降算法(DCD)和信赖域算法.虽然Hsieh等[11−12]的模型和算法被广泛应用在文本挖掘中,但这些模型和算法主要解决了标准的多分类和回归问题,而在顺序回归模型中还没有得到应用.所以该文提出能快速求解基于L2损失的非平行支持向量回归机的算法.

本文提出一种基于L2损失的线性非平行支持向量顺序回归模型.从目前研究来看,这是在顺序回归领域中第一个处理大规模问题的相关工作.此外,针对该模型,该文设计了两种求解该模型的算法并比较了两种算法的性能表现.

本文组织结构如下:第1节介绍基于L1损失的NPSVOR模型.第2节介绍本文提出的基于L2损失的线性NPSVOR(L2-NPSVOR)模型,并给出其对偶模型.第3节研究求解L2-NPSVOR模型的优化算法,从原问题和对偶问题两个角度分别给出了信赖域牛顿算法和对偶坐标下降算法.第4节主要介绍数值实验,将提出的L2-NPSVOR模型与其他相关模型进行分析比较,验证模型的有效性.最后,对本文研究工作进行总结.

1 非平行支持向量回归机

在顺序回归问题中,每个训练样本均由一个特征向量和一个有序标签组成.假设顺序回归问题有个不同的具有有序结构的类别,为不失一般性,我们用连续整数1,2表示其类别,用表示样本的数量.则顺序回归样本集可以表示为:

文献[10]提出的非平行支持向量顺序回归模型(NPSVOR),其可以在原空间上学习多个非平行的超平面,对数据分布具有更好的适应性.并在性能上优于其他基于SVM的方法.对于类的顺序回归问题,NPSVOR 针对每个类别构建有序三元分解学习一个超平面,即给定,首先对每个索引建立三个索引集:和.其中是的标签. 然后,学习一个映射,建立如下优化模型

在模型式(1)中,第一项为正则项,第二项和第三项为L1损失项,其中第二项是要求学习的超平面尽可能考虑第类样本,第三项要求其他类样本离该超平面尽可能远,且其中标签大于的样本和标签小于的样本分别位于该超平面两侧,以更好地利用标签的有序信息.值得强调的是,学习的个子优化模型(1)相互独立,因而可并行学习.

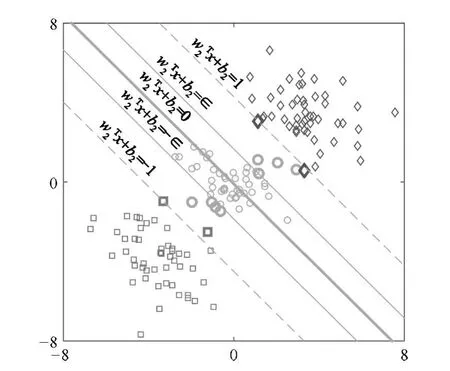
图1 非平行支持向量顺序回归的几何解释(以类别2超平面构建为例)Fig.1 Geometric interpretation of NPSVOR(It shows the construction of the 2-th proximal hyperplane)

若第类对应的模型式(1)的解为,那么关于第类的最优超平面即为,其中. 预测准则被定义为:

2 基于L2损失的线性非平行支持向量顺序回归机

本节将在NPSVOR模型基础上描述本文提出的基于L2损失(均方Hinge损失)的线性NPSVOR模型.考虑到模型(1)中L1损失对损失的惩罚是线性关系,而顺序回归问题建模目标是使预测标签与真实标签尽可能接近,这促使我们考虑采用L2损失函数,其对于较大的损失给予更大惩罚,使模型尽可能避免产生较大偏差预测.

据此,我们考虑建立L2损失线性NPSVOR模型

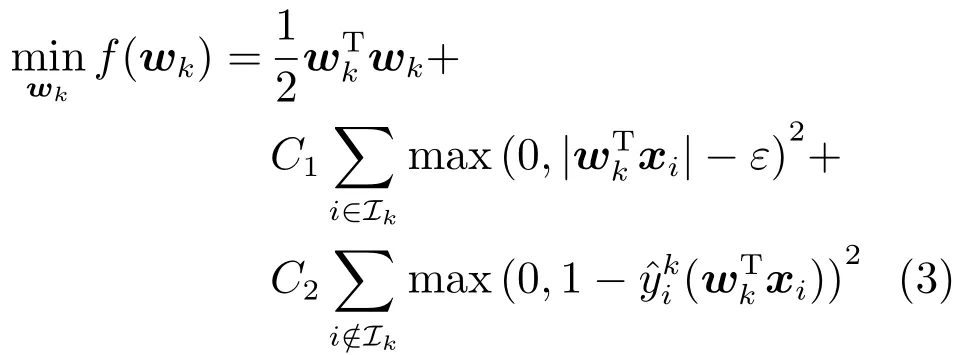
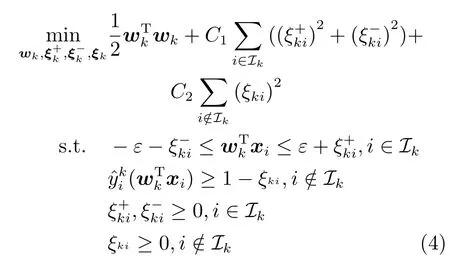
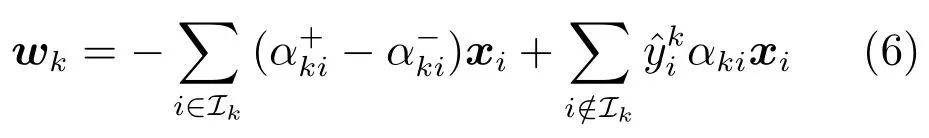
对于具有类的顺序回归问题,L2-NPSVOR由个子优化模型式(3)(或对偶问题式(5))组成.

3 训练算法

在本节中,我们将针对L2-NPSVOR模型,从原问题及其对偶问题两个角度,分别设计了信赖域牛顿算法和对偶坐标下降算法求解该模型.由于不同k对应的原问题式(3)及其对偶问题式(5)具有相同形式,为了方便讨论,在不引起混淆的情况下,我们将忽略模型式(3)和式(5)中的下标k.

3.1 信赖域牛顿法

信赖域牛顿算法(TrustregionNewton method,TRON)[13]是一种求解可微的无约束或有界约束问题的广义优化算法.Ho和Lin等研究了L2损失SVC和SVR以及Logistic回归问题的TRON算法[12−14].这里将该算法应用于L2-NPSVOR模型的求解.

采用TRON算法求解原问题(3),优化过程包含两层迭代:在第步外迭代中,给定,TRON算法构造在信赖域半径下的二次优化问题,即

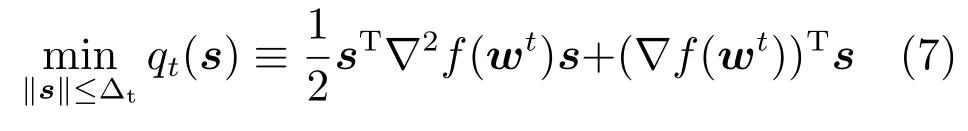
然后,在内层迭代中,求解该模型获得拟牛顿方向s.TRON 算法根据近似函数调整优化半径,具体调整方法参见文献[14].在构造二次优化问题时,需要计算梯度和Hessian矩阵.由于连续可微,存在梯度

其中

其中I为m阶的单位矩阵,D为n阶对角矩阵且

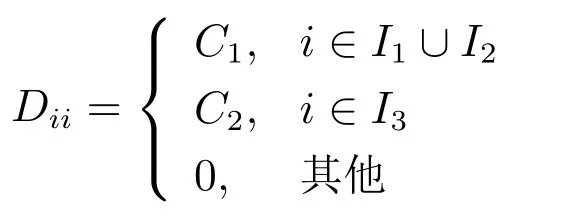
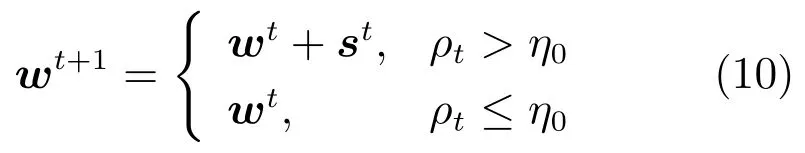
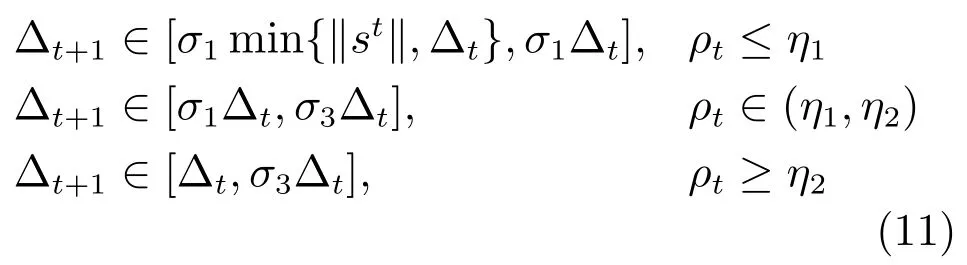
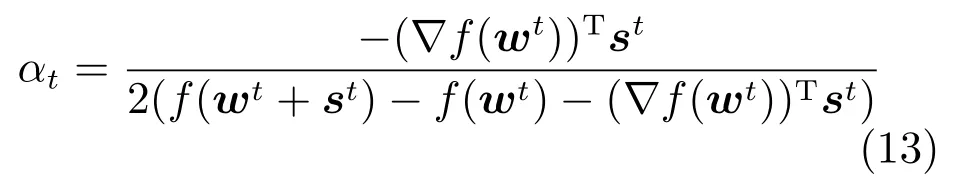
对于算法终止条件,我们考察算法第k次迭代步时目标函数的梯度相对初始梯度关系,以及样本类别样本规模,建立如下终止条件

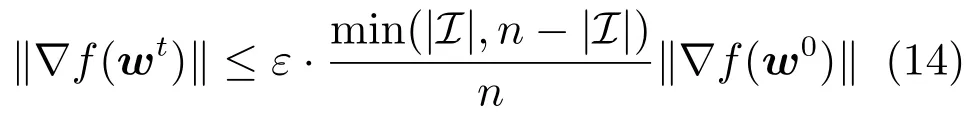
其中为给定终止精度,表示指标集元素个数,n为训练样本个数.

算法1给出了NPSVOR的信赖域牛顿法算法主要步骤.

算法 1.TRON:信赖域牛顿算法求解L2-NPSVOR的子模型式(3)

2)根据类别k定义.

算法1的效率主要依赖于是否能快速求解子优化问题式(7).由于目标函数的广义Hessian矩阵式(8)是m×m阶,对于高维问题直接计算该矩阵会使得内存难以存储.同时,由于样本矩阵X高度稀疏,可采用共轭梯度算法进行求解,因此只需要在算法优化过程中计算和存储Hessian矩阵式(8)与向量的乘积,即

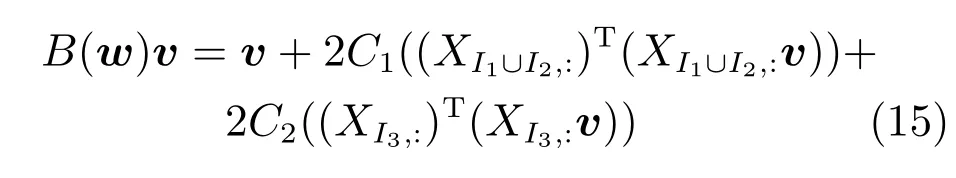
算法2给出了求解问题(7)的共轭梯度算法过程.

算法2.共轭梯度算法近似求解信赖域子问题(7)

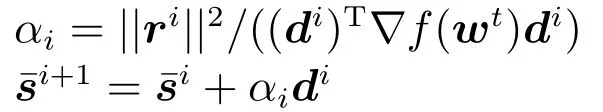
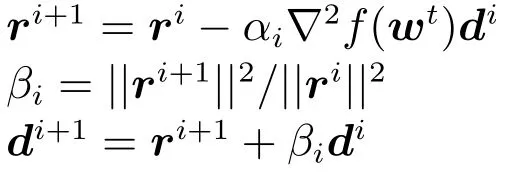
3.2 对偶坐标下降算法

坐标下降算法(Coordinate descent method,CD)是一种无约束优化技术,被用于求解大规模线性SVM模型.Chang等[9]利用CD算法求解L2损失的线性SVM 模型的原始问题,实验表明这种方法可以快速获取模型的解.Hsieh等[11]提出对偶坐标下降算法(Dual coordinate descent method,DCD)求解线性SVM 模型,即在L1和L2损失的线性SVM 的对偶模型上利用CD算法,并采用Shrinking和随机置换优化样本序列的加速技术.当数据的规模和特征维度规模都比较大时,CD算法比其他算法在求解线性SVM模型上能获得更好的效果[11,16].Yuan等[17]将DCD算法应用于求解L1正则化的优化问题.Tseng和Yun[18]系统讨论了L1正则优化问题的分解算法,给出分解算法的一般性框架[12].将DCD算法扩展到求解大规模SVR问题中,但采用了与文献[11]中不同的Shrinking准则和算法终止策略,研究表明这种策略在回归问题中可以快速获得优化模型的解.本节将利用DCD算法求解基于L2损失的线性NPSVOR,实现大规模顺序回归问题的求解.

忽略原问题式(3)的下标k,其对偶问题式(5)可写为:

其中与对偶变量相关

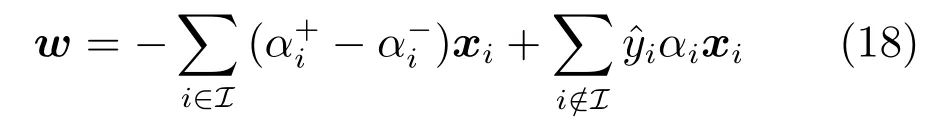
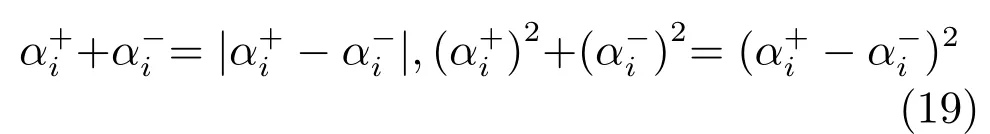
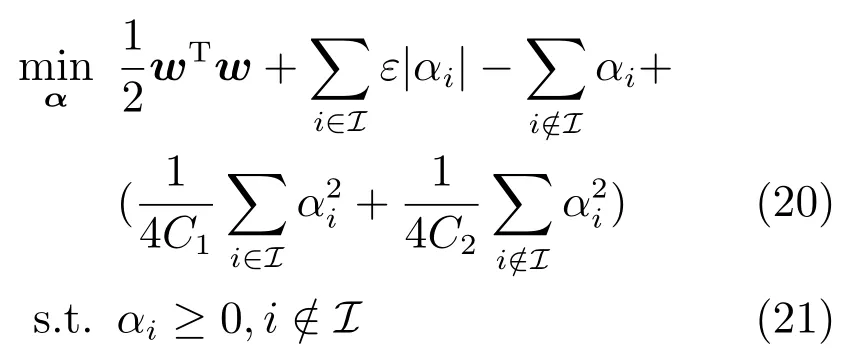
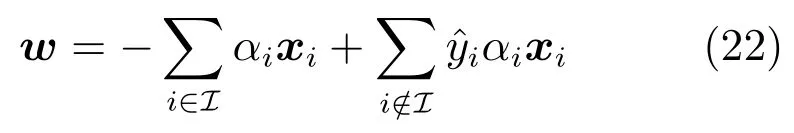
对偶坐标下降算法,每次仅更新一个变量,同时固定其他变量.由于目标函数变量中关于存在不可微项,这里对的变量分别讨论.

根据软阈值的方法可知,优化问题的解为

其中

在算法迭代中,需要判断优化变量是否达到最优性条件,定义优化目标函数关于的投影梯度为

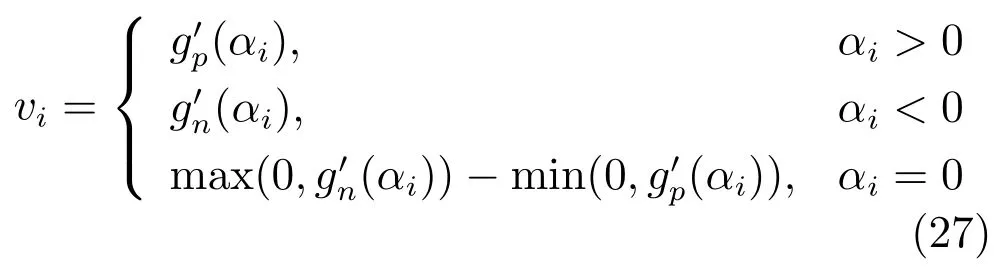
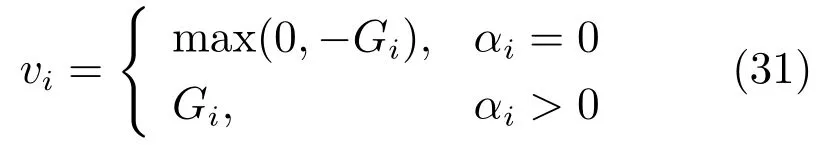
算法3.DCD:坐标下降法求解L2-NPSVOR的对偶问题(5)

3)while不满足最优性条件:do(4)

do步骤5),6),7).

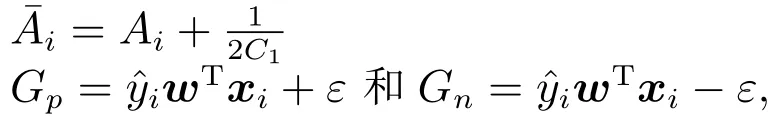
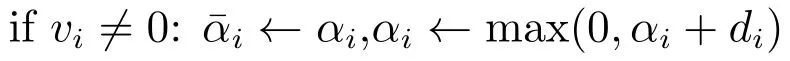
关于终止条件,我们可以采用文献[17]的终止条件,即

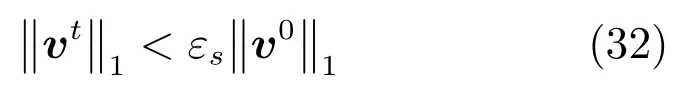
Shrinking策略[19],是一种算法加速技术,在算法迭代训练时删去一些值不变的变量,通过减少优化问题的变量规模实现对算法的加速.该策略常被用于SVM 的分解算法,只是不同的算法和模型在具体操作上有所不同.在本文的DCD算法中,也采用了该技术,即考虑在算法的有序迭代中,删除达到约束边界的最优变量(即)以及不可微点.对于变量,Shrinking条件为:

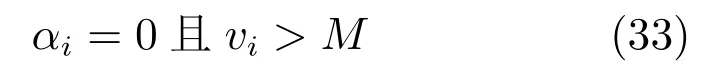
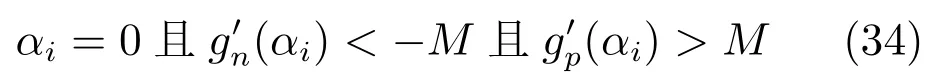
其中

这里取梯度违反值绝对值的最大值式(35)作为Shrinking阈值条件,并考察梯度违反值与初始v0值缩小比例式(32)进行算法终止.在后面实验中,我们将进一步对比在设计大规模线性SVM 的DCD算法中提出的Shrinking技术和终止策略[11],即对梯度违反值正负值分别维持阈值M,m,然后并将作为算法终止条件(具体见文献[11]),以说明本文算法设计的合理性.

4 数值实验

为验证提出的L2-NPSVOR模型及算法的有效性,本文在多个数据集上与其他基于SVM 的顺序回归模型进行了性能比较.其中比较的模型包括:L1-NPSVOR、SVM、SVR、RedSVM 等.此外,本文还比较了TRON和DCD在L2损失的NPSVOR模型的算法效率.最后本文分析了L2-NPSVOR模型对参数的敏感性.TRON和DCD算法均在LIBLINEAR框架基础上用C++实现1算法代码已上传至https://github.com/huadong2014/LinearNPSVOR/.,实验平台为Intel Xeon 2.0GHz CPU(E5504),4MB cache,内存4GB,Linux系统.

4.1 实验数据准备与评价标准

针对大规模高维稀疏的顺序回归问题,目前还缺少相关的研究.这里我们收集并整理了部分文本顺序回归数据集,这些数据来自情感分析、电影评论、Amazon商品评论等多个领域,具体数据集如下:

1)TripAdvisor2数据集取自http://www.cs.virginia.edu/～hw5x/dataset.html,是一个酒店评论数据集,最早被用于文本潜在语义分析[20].每条评论有一个1至5颗星的打分.

2)Treebank3http://nlp.stanford.edu/sentiment/,来自斯坦福大学构建的情感数据库Treebank,每条数据对应一个来自{very negative,negative,neutral,positive,very positive}的标签.

3)MovieReview[21],电影评论数据集4scale dataset v1.0:http://www.cs.cornell.edu/people/pabo/movie-review-data/.顺序标签是从连续值[0,1]离散化得到,即a)rating≤0.3,b)0.4≤rating≤0.5,c)0.6≤rating≤0.7,d)0.8≤rating.该数据集常被用于情感分析.

4)LargeMovie5http://ai.stanford.edu/～amaas/data/sentiment/,是一个包含8种情感类别的电影评论数据.

5)Amazon产品评论,有8个数据集,来自两个数据资源网站:其中4个数据集来自文献[20],包括AmazonMp3,VideoSurveillance,Mobilephone,Cameras6http://sifaka.cs.uiuc.edu/～wang296/Data/index.html;另外4个数据集(Electronics,Health-Care,AppsAndroid,HomeKitchen)[22−23]来自 A-mazon产品评论数据集7Amazon product reviews datasets:http://jmcauley.ucsd.edu/data/amazon/,所有数据均是文本评论,且有5个类别.由于实际数据集类别样本分布不均衡,为了不影响模型测试表现,这里对数据集进行降采样得到平衡数据集.

以上数据集均为文本数据,故本文对这些数据进行下列预处理:词干化、去停用词、删除词频小于3次的词,以及在所有文本出现的频率大于50%或出现少于2次的词.此外,我们采用unigram,bigram作为特征,利用TF-IDF技术提取文本特征.为了方便实验算法分析和方法比较,将每个数据集随机划分为两部分,即取20%条数据作为测试集,剩余80%条数据作为训练集.数据集的统计描述见表1所示,其特征包括样本规模、特征维数、训练集非零元素个数等.

关于评价标准,由于顺序回归问题与普通多分类问题不同,预测标准是预测标签与真实标签尽可能接近,因此,这里采用平均绝对误差(Mean absolute error,MAE)和平均均方误差(Mean square error,MSE)作为评价准则,即给定预测标签和实际标签,MAE和MSE定义如下

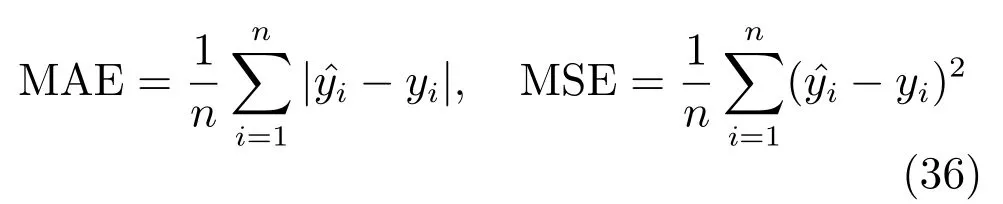
该指标被广泛用于刻画顺序回归模型预测与实际标签的接近程度[6−7,24−25].

4.2 L2-NPSVOR与其他模型比较

本节我们测试线性L2-NPSVOR的泛化效果,并与其他SVM相关方法比较,比较方法具体如下:

1)SVC[11],将顺序回归看成普通多分类问题处理的朴素方法.文献[11]给出了线性SVM模型的DCD算法,在算法中采用了随机置换和Shinking加速技术.该算法已经实现并集成在著名的LIBLINEAR软件包中,采用one-vs-all的方式策略进行多分类预测.

2)SVR[12],将顺序回归标签看成普通数值,采用数值回归的方式进行处理,同样属于一种朴素方法.SVR模型预测值是连续的数值,本文对预测后的连续数值按照相邻的整数离散成相应的类别标签.文献[12]给出了线性SVR的DCD求解算法,并在LIBLINEAR中实现,这里仅对预测函数作了修改.

3)RedSVM[7],对于p类顺序回归问题,其学习一个线性映射将样本映射到一维实数轴上,在该数轴上寻找p−1个具有最大划分间隔的阈值点,将直线分成p个连续的区间段进行预测.文献[7]提出一种处理顺序回归的框架,将顺序回归问题转化为一个二元分类问题,对样本通过扩展将其转化为二分类样本,其中当,否则.

4)L1-NPSVOR[10],基于L1损失的NPSVOR,属于有序分解模型,根据标签有序信息,对每个类别均构造一个三划分并学习一个超平面,从而构建了优化模型式(1),可直接将文献[11]的DCD算法直接扩展求解其对偶问题.

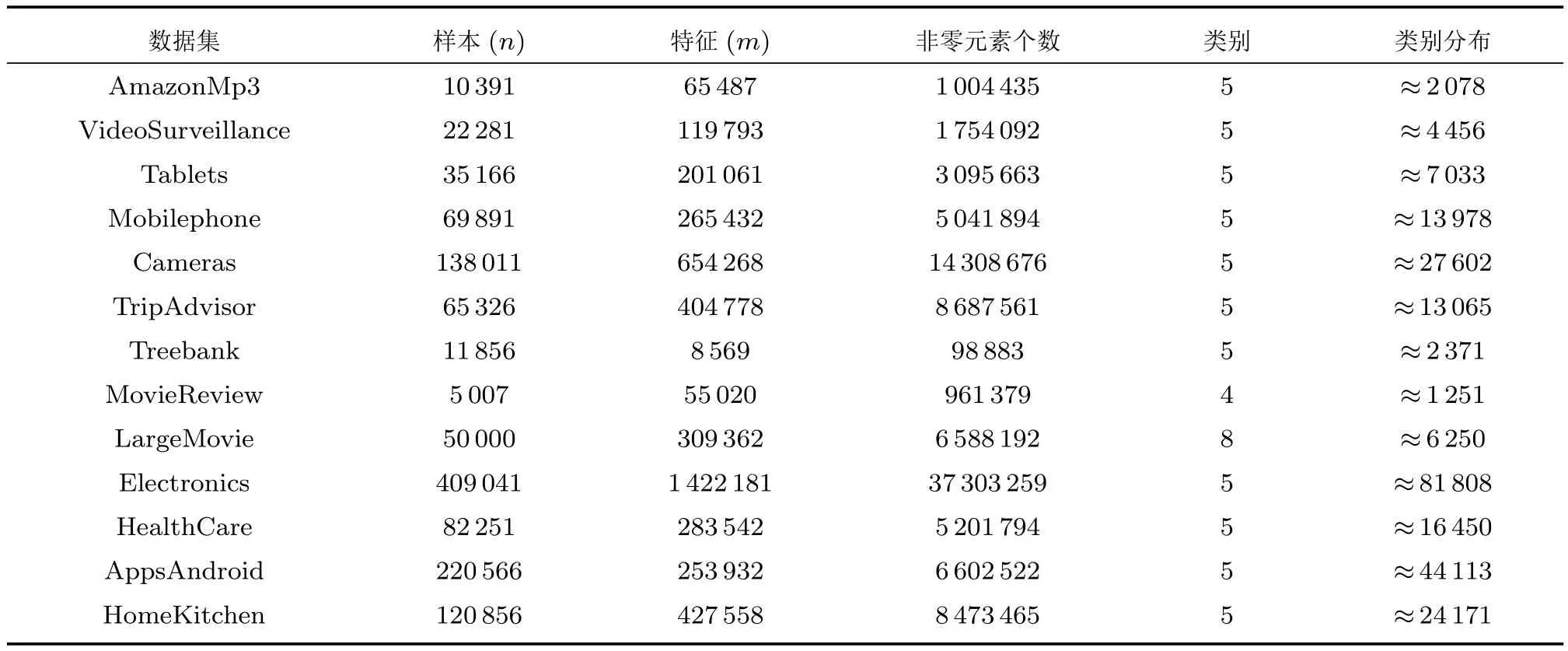
表1 数据集特征描述Table 1 Data statistics

5)L2-NPSVOR(TRON),即L2损失的NPSVOR,采用信赖域牛顿法(见算法1)求解,共轭梯度算法(算法2)求解信赖域子问题式(7).

6)L2-NPSVOR (DCD),即L2损失的NPSVOR,采用对偶坐标下降法(见算法3)求解,终止条件为式(32),Shrinking策略为式(33)和式(34).

该实验在训练集上进行5-折交叉验证进行参数选择,参数选择范围设定在.以MAE作为交叉验证选参的标准,通过参数选择后的最优参数作为模型训练的参数.关于实验参数设置方面,基于DCD算法求解的模型终止精度均设为0.1,和均采用0向量作为初始化,TRON的终止精度设定为0.001.另外,为公平起见,在NPSVOR算法中该实验固定参数值为0.1,,并与其他模型中的采用同样的选参方式,除RedSVM模型8需要注意的是,因为目前还没有针对顺序回归问题提出的大规模求解算法,RedSVM模型只有非线性模型的求解算法,故本文对线性RedSVM算法求解时采用文献[7]中DCD算法对RedSVM的线性版本进行实现.,其他模型均采用有偏置项模型.实验数据集如表1所示.表2给出了各模型在不同数据集上MAE、MSE值和训练时间(Time),表中每行最好的结果均已经加粗显示.表2的最后列出了各方法在所有数据集上关于MAE、MSE和训练时间的平均排序,以方便比较各模型之间的性能.

从表2的结果中,通过观察可以得到以下几点结论:

1)根据各方法在所有数据集上平均排序可以看出,L2-NPSVOR较其他方法在MAE和MSE上,取得了最好的预测效果.虽然L2-NPSVOR在TRON和DCD算法得到的预测效果接近,但DCD在总体上得到了更好的MAE和MSE值,算法的训练时间相对TRON优势明显.

2)RedSVM模型在非线性情况下表现突出[4],但在大规模数据集的表现略低于朴素方法线性L1/L2-SVC.

3)对比L1-NPSVOR和L2-NPSVOR,采用L2损失的模型在MAE、MSE优于L1-NPSVOR模型,这与我们的预期一致,即顺序回归问题预测要求预测标签与实际标签尽可能接近,L2损失对于损失偏差较大的样本给予更大的惩罚,可得到预测偏差更小的模型.此外,基于L2损失的NPSVOR在DCD算法下可以得到更快的优化速度.

4)在算法的训练时间上,基于DCD算法的L2-NPSVOR获得了除SVR外最快的训练速度.尽管SVR在时间上具有优势,但其在顺序回归上的预测结果相对较差,这也说明将顺序回归问题等同于数值回归存在一定的缺陷.

4.3 TRON与DCD算法比较

本文针对NPSVOR提出了信赖域牛顿算法和对偶坐标下降算法,这里我们对算法效率进行比较.假设原问题的优化目标函数为,通过观察算法训练过程中目标函数值与最优值目标函数值的接近程度,即来比较算法效率.为说明本文算法设计的合理性,考虑以下四种情形:

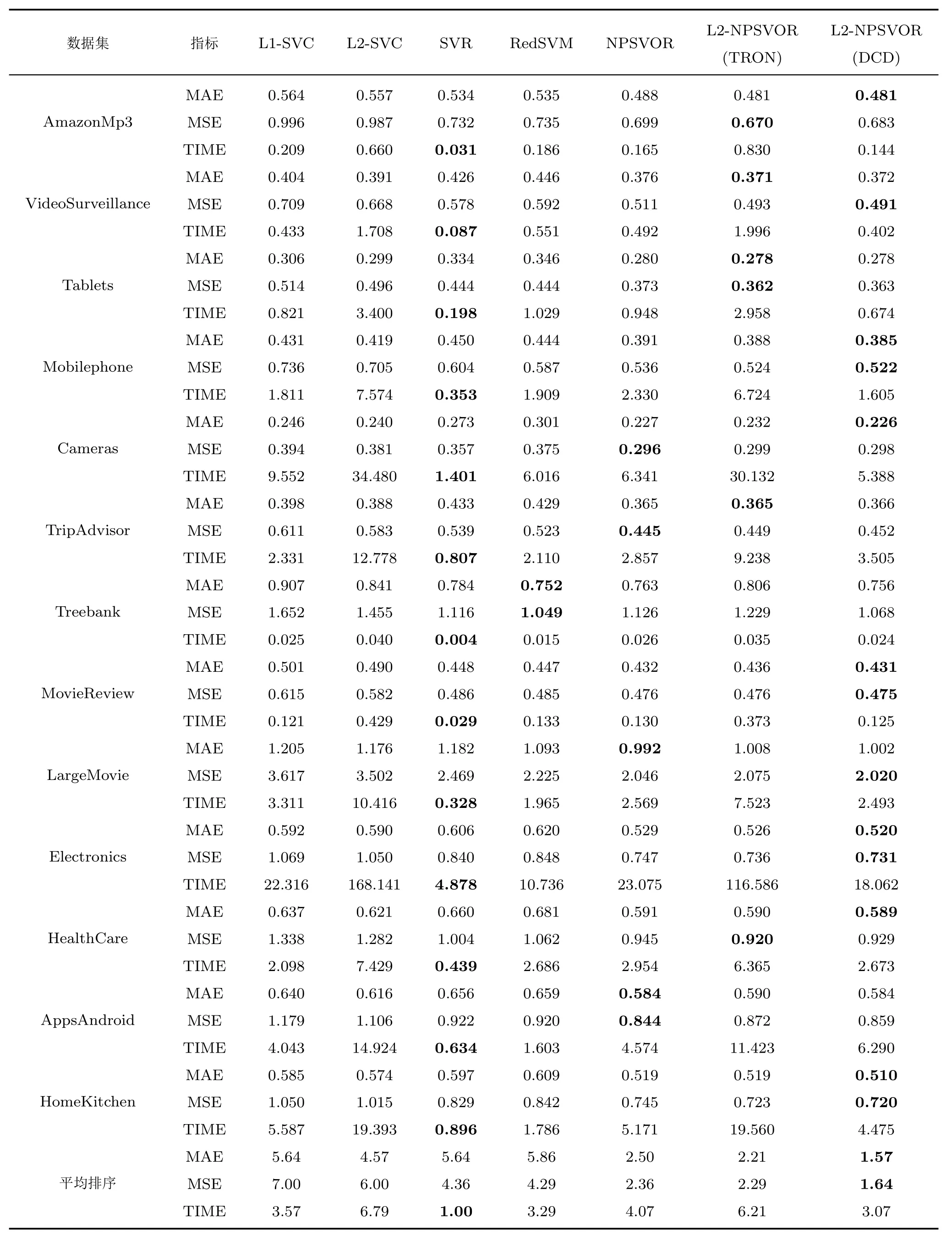
表2 方法在各数据集上测试结果,包括MAE、MSE和最优参数下的训练时间(s)Table 2 Test results for each dataset and method,including MAE,MSE and training time(s)

TRON:即本文给出的信赖域牛顿算法1,在算法中NPSVOR各子模型独立求解,均初始化,可分布并行求解各子模型.为方便比较,这里仅考虑串行求解方式.

TRON(WS):在利用TRON算法求解NPSVOR各子模型时,可采用暖启动策略(Warm start,WS).由于在NPSVOR模型中,每个子模型的超平面是基于有序三元分解建立的,其是根据标签的有序结构信息得到,因而相邻类别对应的超平面相对比较接近,对应的解具有相似的结构,即.如果依次求解对应的模型,在求解第k+1个子模型时,可以利用第k个模型的解作为其初始解,这样可以利用顺序回归的特有性质来加速模型的求解.

DCD-M:即本文给出的对偶坐标下降算法3.算法中采用了Yuan等[17]给出的终止准则和Shrinking策略,即采用最优梯度违反值的绝对值最大值式(35)作为判断最优性条件的阈值.

DCD-Mm:Hsieh等[11]在设计线性SVM的对偶坐标下降算法中,根据梯度投影的最大幅度值作为终止条件的判断依据,并根据上下振幅值作为Shrinking阈值,将该策略应用到文本的DCD算法中,即Shrinking条件为,当时,

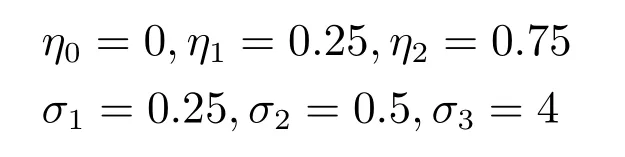
在训练集上进行训练,记录目标函数值变化情况.由于L2-NPSVOR对于每个类别均需要求解一个子优化模型,图2仅展示类别3对应的子优化模型(即k=3)绝对目标函数差训练时间的变化.

从图2中,我们可以观察到:1)采用暖启动的TRON算法TRON(WS)在其中6个数据集上有较为明显的加速,但在短的训练时间内,加速不明显.2)目标函数的在DCD-M算法优化下在给出的8个数据集中比TRON算法高效并且获得了更低的目标函数值,DCD-M算法优势明显.3)DCD-Mm采用文献[11]的终止条件和Shrinking策略,实验表明目标函数值过早趋于平稳,并且不能够及时有效终止算法.

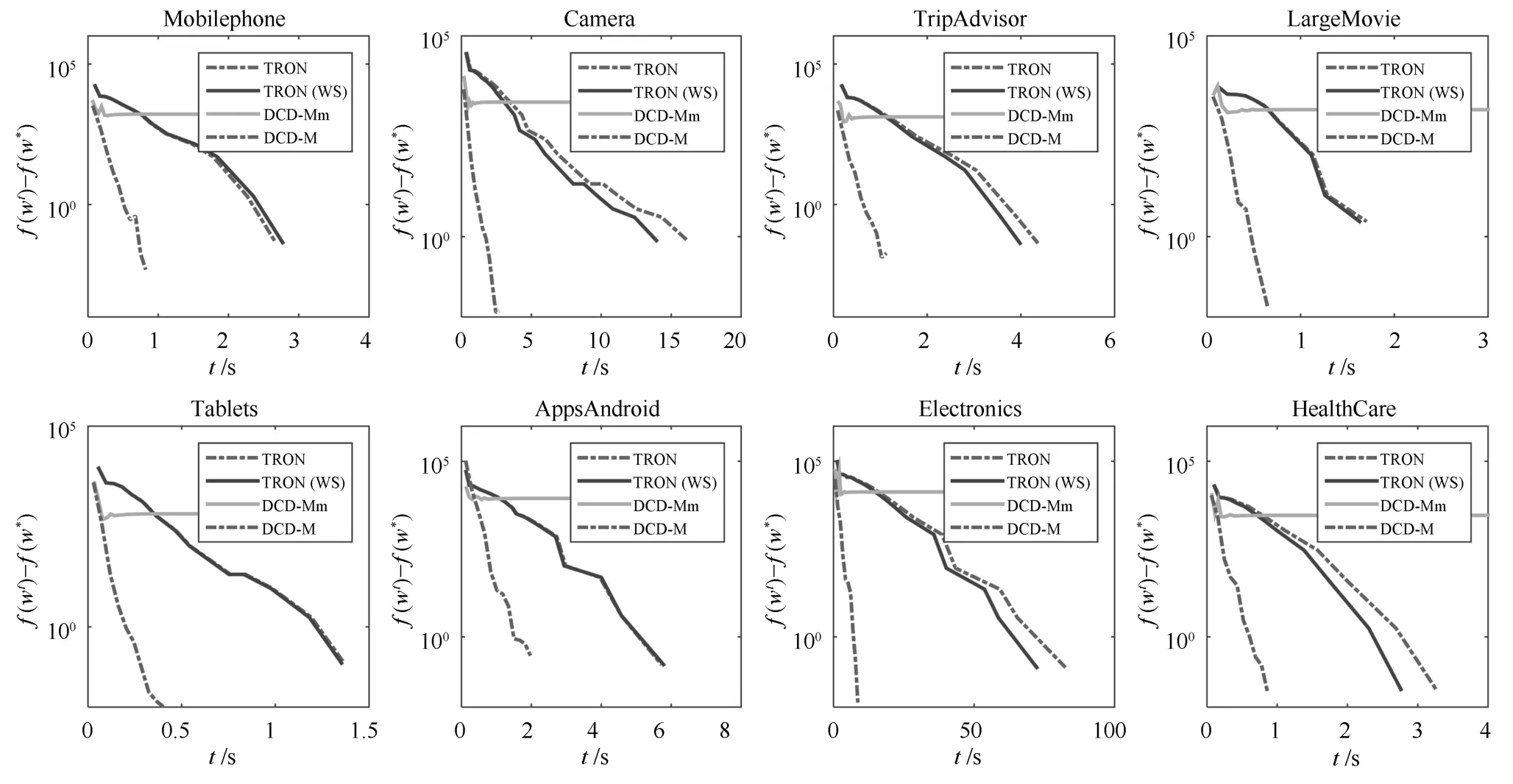
图2 TRON,TRON(WS),DCD-M and DCD-Mm在8个数据集上的比较(这里展示了类别3对应的优化问题).横坐标是时间,纵坐标为L2-NPSVOR 原问题目标函数的的值Fig.2 Comparison of TRON,TRON(WS),DCD-M and DCD-Mm on eight datasets(Show the optimization model for rank 3).The horizontal axis is training time in seconds and the vertical axis is the difference between

4.4 L1-NPSVOR和L2-NPSVOR参数敏感性

参数选择通常十分耗时,故我们期望得到的模型对参数不敏感,即参数值的变化不会有较大的测试结果变化.本节实验将比较L1-NPSVOR和L2-NPSVOR关于MAE和MSE随参数值C改变的变化情况(限定并记为C),采用DCD算法求解.实验选择与第4.3节相同的8个数据集进行实验,参数C的变化范围设定为{2−5,2−4,···,25},采用 5 折交叉验证得到每个参数值下的测试MAE/MSE值.MAE和MSE变化趋势分别如图3和图4所示.

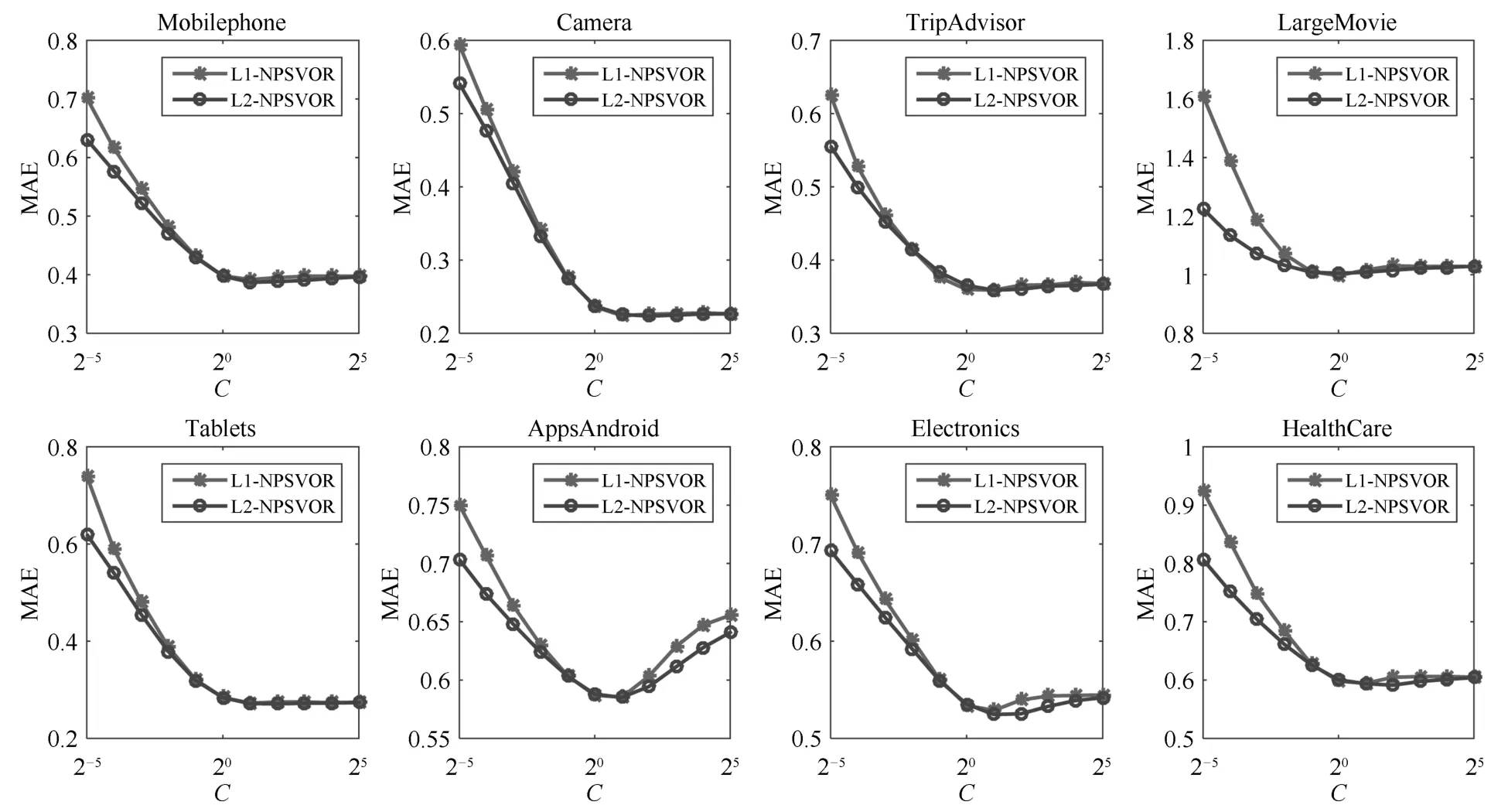
图3 L1/L2-NPSVOR的MAE分别随参数C变化Fig.3 Test MAE results of L1/L2-NPSVOR change with parameterCon eight datasets

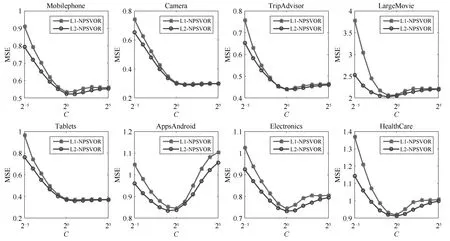
图4 L1/L2-NPSVOR的MSE分别随参数变化Fig.4 Test MSE results of L1/L2-NPSVOR change with parameteron eight datasets

从图3和图4中可以观察得到,基于L2损失的NPSVOR在MAE/MSE上随参数C变化相对平稳,变化幅度均低于采用L1损失的对应结果,尤其是在参数值C较小的情况下,在此情形下,L1-/L2-NPSVOR均在训练数据集上出现欠拟合问题,但是由于L2损失对损失的惩罚要高于L1损失,故欠拟合问题严重性相对较弱一些.另外,从图4中最后3个数据集(Apps Android、Electronics和Health Care)对比看出,L2损失在MSE上有显著地提高.以上结果表明,L2损失对参数C的敏感性低于L1损失,即利用L2损失,可以更容易选出较合适的参数.

5 结束语

本文针对大规模、高维、稀疏的顺序回归问题,考虑到L2损失的引入对偏离较大的点给予更大的惩罚,使得预测标签与真实标签更加接近,而线性模型的提出能成功解决大规模数据面对的速度及内存消耗问题,所以本文提出基于L2损失的线性非平行支持向量顺序回归模型—L2-NPSVOR.另外本文从原问题及其对偶问题两个角度,分别设计了信赖域牛顿算法和对偶坐标下降算法求解该模型.其中在TRON算法中,考虑到顺序回归相邻的超平面具有相似的解,在算法求解时提出暖启动的方法.最后,为验证模型及算法的有效性,本文在收集的大量文本顺序回归数据上对提出的模型及算法进行了分析和比较.结果表明,相比其他基于SVM的顺序回归模型,L2-NPSVOR在性能上表现最优;关于求解算法,TRON算法能够获得比DCD更加精确的解,但当样本维数远远高于样本数时,DCD算法比TRON更加高效.