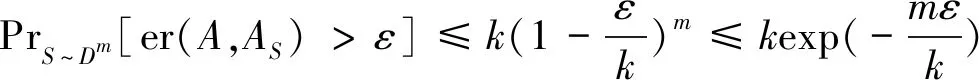二维欧氏空间内线性凸区域概念的PAC学习算法
许道云
(贵州大学 计算机科学与技术学院,贵州 贵阳 550025)
在机器学习中,对给定实例进行分类是一种基本处理方法,其中二分类是重要而基础的分类问题。当实例空间较大或复杂时,精准分类变得复杂或困难,依采样进行近似分类显得有效和实用。可能近似正确(Probably Approximately Correct, PAC)算法提供了一种学习架构,其原理来源于依概率收敛假设。假定实例空间依赖于某个分布,通过独立取样得到容量为m的样本S,如果存在一个算法A能够产生一个输出函数hS,当m趋于无穷大时,hS依概率收敛于目标函数c是PAC可学习的。形式上,对于任意给的误差参数0<ε<1以及可靠性参数0<δ<1,存在一个正整数M,当样本容量m超过M时,算法输出一个近似分类函数hS,至少以概率为(1-δ)确保hS与目标分类函数c的误差不超过ε。如果存在这样的算法,其样本复杂性M和算法的时间复杂性受1/ε,1/δ的多项式界,则称目标概念c是可以有效PAC学习的。PAC学习中,往往加强到对目标概念集C、任意分布D下寻找有效PAC学习算法。如果这样的算法存在,则称概念集C是可以有效PAC学习的。
在本文中,假定实例空间X为二维欧氏空间R2,R2的一个子集的特征函数c:R2→{0,1}规定一个概念。文章重点讨论有界线性凸区域规定的概念的PAC学习理论和方法,线性凸区域是由一组线性不等式界定的区域{(x,y):aix+biy≤ci(i=1,2,……,k)},有界性指区域内的点被一个有界矩形(或圆)包含,目标概念c定义为:c(x,y)=1⟺aix+biy≤ci(i=1,2,……,k)成立。 本文给出了这类概念学习的理论和方法,并证明了它是可以有效PAC学习的。相关的理论和方法容易推广到n维欧氏空间由超平面界定的有界凸区域规定的目标概念的PAC学习。
这类概念的学习可以用于大范围线性规划问题可行解的近似识别。
1 PAC学习基础知识
假定X为实例(数据)空间,有限集Y作为数据标记集,通常取Y={0,1}(或{-1,+1})。一个函数f:X→Y决定X中数据一个划分(分类):f(x)=f(y)当且仅当x,y属于同一类。X的一个子集称为一个概念,可用其特征函数表示该子集。因此,形式上一个函数c:X→{0,1}表示一个概念,由概念构成的集合C称为概念集。本文中相关的基本知识来自于文献[1], 更多的实例和应用可参考文献[2-4]。
机器学习的任务是通过带某种样本(或经验)的算法学习方式得到一个近似函数c′:X→{0,1},其中c与c′之间的“距离”误差通常用概率表示er(c,c′):=Prx~D[c(x)≠c′(x)],其中D表示空间X上的某个分布,而c′是可以由算法产生。
对于给定的概念集C, 以C中元作为目标概念,能够由算法产生的所有可能的近似函数构成的集合称为假设空间H。一般C与H不同,通常假定C⊆H。对于一个目标概念c及一个假设h∈H,其泛化误差定义为:
er(c,h) =Prx~D[c(x)≠h(x)]
=Ex~D[1c(x)≠h(x)],
(1)
其中,函数1P为指性函数(条件P成立时取1,否则取0)。当c固定时,在不引起歧义的情况下,简记为:R(h)=Prx~D[c(x)≠h(x)]。它是随机变量1c(x)≠h(x)的数学期望,理论上是一个整体概念。
对于目标概念c的算法学习,通常是采用抽样学习,即依分布D下独立取样得到一个大小为m样本S={x1,x2,……,xn},对于样本S, 假定其样本点的分类标记可观察到,从而形成一个带标记的数据集:
{(x1,y1),(x2,y2),……,(xn,yn)},
基于样本S及假设h,以如下公式定义h的经验误差:
(2)

对于给定的目标概念c以及样本S={x1,x2,……,xn},带标样本集为{(x1,y1),(x2,y2),……,(xn,yn)},如果c(xi)=yi(1≤i≤m),称样本S与目标概念c一致。一般选择一个训练集(作为样本集)与目标概念c一致。
在学习算法中,有时可以通过目标概念c对样本S中样本点进行标记。如:目标概念为一个矩形cR时,落入cR内的样本点被标记为1,否则标记为0。此时,样本S与目标概念cR自然一致。
对一个假设h, 如果h(xi)=yi(1≤i≤m),称假设h与样本S一致。
对于学习算法A, 如果对于任意的目标概念c及任意独立同分布(i.i.d.)样本S, 以c和S作为算法的输入,算法输出的假设hS与样本S一致,则称算法A为样本一致学习算法。
对于0<ε<1,0<δ<1,视ε为误差参数,δ为可靠性参数,对于给定的目标概念c以及假设空间H,一个假设h被称为ε-good假设,如果泛化误差R(h)≤ε;否则称h为ε-bad假设。
PAC算法的核心问题是:设计一个学习算法A,使得由算法通过样本学习(输出)的hS是ε-bad假设的概率小于δ;或者说,通过对样本的学习,算法输出的hS是ε-good假设的概率至少是1-δ。
形式上表现为:将hS表示为A(S,c)=hS,以示算法A以(S,c)作为输入,输出hS。hS作为一个随机变量函数满足如下条件:
PrS~Dm[er(hS)>ε]<δor
PrS~Dm[er(hS)≤ε]≥1-δ,
(3)
这样的算法(ε,δ)-学习算法,其中m称为算法的样本复杂性。
对于一个目标概念c, 如果对于任意的参数对(ε,δ),存在一个(ε,δ)-学习算法A 满足条件:算法的样本复杂性的下界被一个1/ε,1/δ,size(c)的多项式保护;即,存在一个多项式p(1/ε,1/δ,size(c)),使得对于任意的分布D,当m≥p(1/ε,1/δ,size(c))时,算法输出的假设hS满足(3)式,则称c是通过样本PAC-可学习的,简称PAC-可学习。
进一步,如果算法A是关于1/ε,1/δ,size(c)的一个多项式算法,则称目标概念c是PAC-有效可学习的,对应的算法称为有效的PAC算法。一般,本质上主要依赖于1/ε,1/δ的多项式。
可以看出:PAC算法的主要任务是基于样本S,通过算法从假设空间H是获取一个假设(函数)hS,以其近似目标概念(函数)c,使其在任意给定的参数对0<ε,δ<1及任意分布D下,满足条件(3),并且样本复杂性下界受1/ε,1/δ的多项式保护。有效性则加强到算法本身的时间复杂性受1/ε,1/δ的多项式控制。
对概念c的学习实质上是一种“函数逼近”,只不过这种逼近是依靠增大样本容量提高精度(减小误差),问题是当样本复杂性要求受多项式保护时,如何设计合适的随机算法,以保证当样本量m达到某个多项式p(1/ε,1/δ)级时,得到的hS满足“至少以1-δ的概率使R(hS)≤ε。
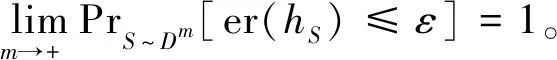
一般,对于给定的目标概念c、以及样本实例S={x1,x2,……,xn},算法产生的hS在S上可能不一致。可能会出现两类错误:正错(1-错):c(xi)=0,但hS(xi)=1;负错(0-错):c(xi)=1,但hS(xi)=0。
如果只产生一类错误,则称算法为单侧随机算法。当样本容量m固定时,算法分析的任务集中在估计概率PrS~Dm[er(hS)>ε]的上界,它是一个以(m,ε)为参数的函数e(m,ε)。最终,令e(m,ε)<δ反解出m≥m(ε,δ),并检验m(ε,δ)被一个1/ε,1/δ的多项式控制。
我们注意到:函数f:X→{0,1}与一个X的子集{x∈X:f(x)=1}一一对应。为方便起见仍然记为f。在不引起歧义的情况下,x∈f指f(x)=1。对于X的一个分布D, 将概率Prx~D[x∈f]=Prx~D[f(x)=1]记为Prx~D[f]。于是,泛化误差er(c,h)=Prx~D[c⊕h],其中⊕表示集合之间的对称差。
对于目标概念c和假设h, 以h近似c的正错误差和负错误差分别为:
er1(c,h)=Prx~D[hc],er0(c,h)=Prx~D[ch]并且er(c,h)=er1(c,h)+er0(c,h)。
用图1表示其误差关系:
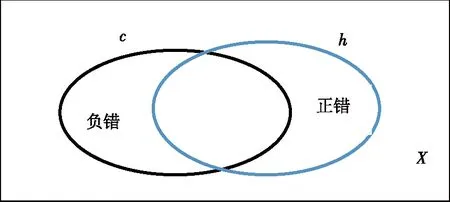
图1 概念c与假设h之间的误差Fig.1 Error between concept c and hypothesish
2 学习算法的样本复杂性估计方法
本节通过一个经典的目标概念学习范例,介绍一种学习算法样本复杂性估计的方法。
取实例空间X为二维欧氏平面R2,标记集取为Y={0,1}。在平面上,边平行于座标轴的矩形称为轴对齐矩形。以轴对齐矩形r作为目标概念cr,对于点x∈R2,cr(x)=1⟺x∈r(含矩形边界)。
考虑如下PAC学习算法A:
(1) 输入一个矩形r;
(2) 依分布D以i.i.d.在平面R2取样S={x1,x2,……,xn};(固定某个分布D)
(3) 记落入矩形r的样本点为Sr,在平面R2取一个含Sr中点的最小轴对齐矩形rS;
(4) 输出rS决定的假设(函数)hS(hS(x)=1⟺
x∈rS(x∈R2))。
可以看出:算法中产生的rS⊆r。从而,输出的假设(函数)hS“只可能出现负错,不会出现正错”。
以下过程是估计样本复杂性:对于任意给定的0<ε<1,估计PrS~Dm[er(hS)>ε]的上界。
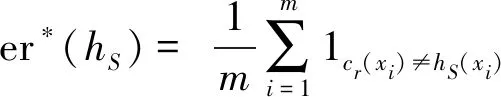
当er(r)≤ε时,即er(r)=Prx~D[x∈r]≤ε。由于rS⊆r,自然有er(rS)=Prx~D[x∈rS]≤ε。从而PrS~Dm[er(hS)≤ε]=1,或PrS~Dm[er(hS)>ε]=0。
因此,不妨假设er(r)=Prx~D[x∈r]>ε。从几何上,视矩形r的面积大于ε。
于是,从r的四条边开始,分别以每条边向r的内部从空矩形开始以线扫描式扩充成四个轴对齐矩形r1,r2,r3,r4,使其满足如下条件:
Prx~D[ri]=ε/4(i=1,2,3,4),
(4)
由于Prx~D[r]>ε,四个小矩形r1,r2,r3,r4的生成是可行的。几何上表现为如图2。
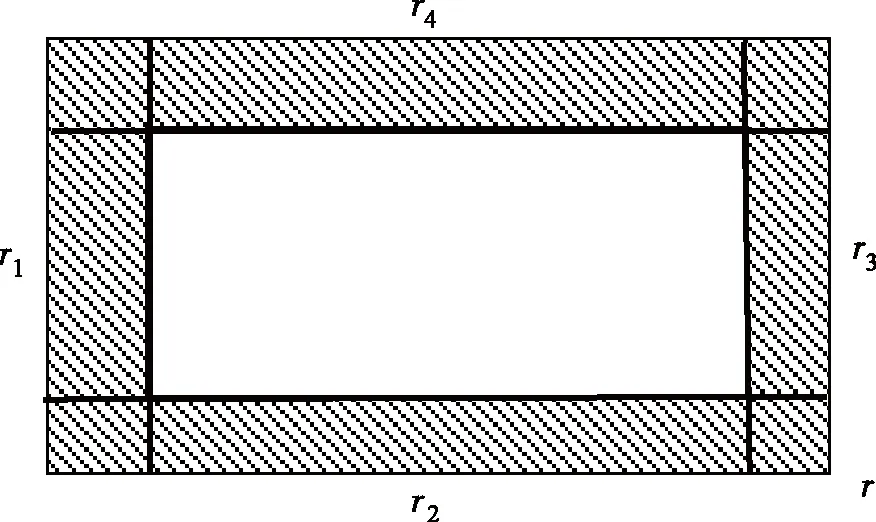
图2 目标概念r内部边缘区域Fig.2 Marginal area inside of traget concept r
由四个小矩形的构造方法,我们有:
Prx~D[r1∪r2∪r3∪r4]
≤Prx~D[r1]+Prx~D[r2]+Prx~D[r3]+Prx~D[r4]=ε。
(5)
直观上,r1,r2,r3,r4构成目标概念内侧的一个ε-环带,简称为r的一个单(内)侧ε-区域。该区域由4个ε/4段构成。
由算法中矩形rS的构造及rS⊆r,er(hS)=Prx~D[r S]。因此,如果er(hS)>ε,则矩形rS至少与r1,r2,r3,r4之一的交为空集。若不然,rS与r1,r2,r3,r4的交都不空,则由轴对齐性质,矩形rS在几何上呈现如图3中虚线矩形状态。
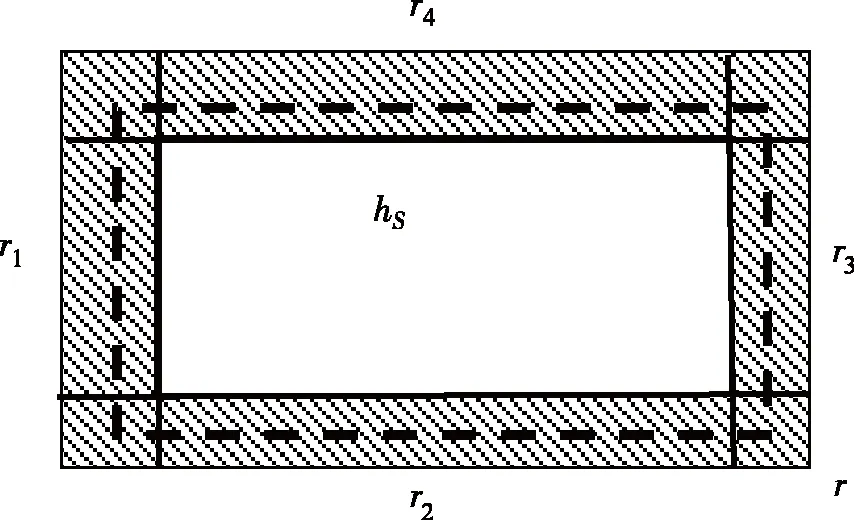
图3 基于样本S的假设hS与4个子区域相交Fig.3 Hypothesie hS based on sample S intersects with four subareas
于是,由rS决定的假设(函数)hS满足:
er(hS)
=Prx~D[r S]
≤Prx~D[r1∪r2∪r3∪r4]
≤Prx~D[r1]+Prx~D[r2]+Prx~D[r3]+Prx~D[r4]
≤ε,
此与er(hS)>ε矛盾。
因此,我们有:如果er(hS)>ε,则rS与r1,r2,r3,r4的之一的交为空集。
不妨设rS∩r1=∅,此时矩形rS在几何上呈现如图4中虚线矩形状态。
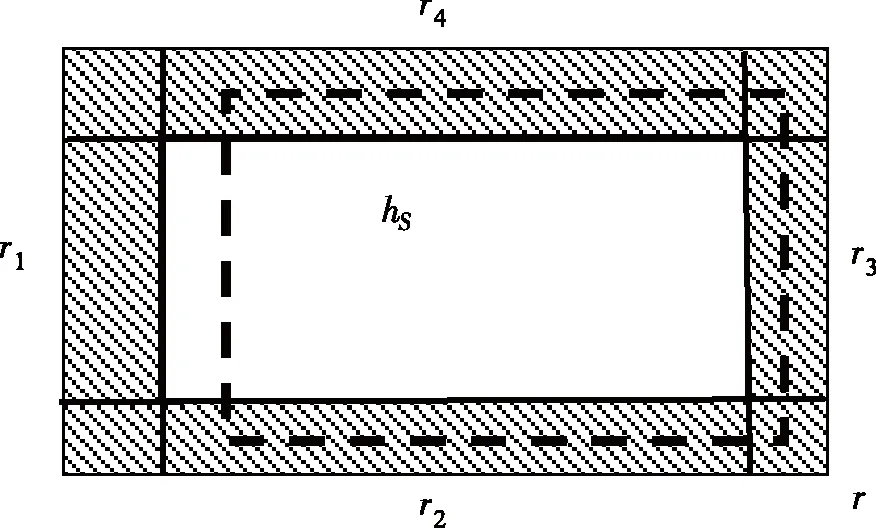
图4 基于样本S的假设hS与4个子区域之一不相交目Fig.4 Hhypothesie hS based on sample S does not intersects with one of four subareas
可见,一次取样事件“rS∩r1=∅”发生等价于“样本点不落入r1”,其概率至多为(1-ε/4)。
从而,m次独立取样“m个样本点不落入r1” 的概率至多为(1-ε/4)m。因此,我们有:
PrS~Dm[er(hS)>ε]

≤4(1-ε/4)m。
(6)
由不等式1-x
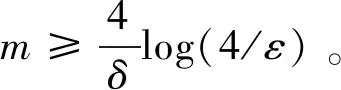
注:在学习算法A的第(3)步中,我们可以取一个包含目标矩形r,并且不含落在r外侧的样本点的最大轴对齐矩形作为hS。 此时算法“只出现正错,而不会出现负错”。讨论方法是对称的。
上述方法的主要思想是:
构造目标概念c的一个单侧概率ε-区域,该区域由4个ε/4段构成。在er(hS)>ε条件下,算法基于样本S产生的假设rS至少与r1,r2,r3,r4的之一不相交(比如:不落入r1)。由此,对于一次取样,事件“rS∩r1=∅”发生的概率至多为(1-ε/4),m次取样不落入该子区域的概率至多为(1-ε/4)m。由(6)式估计样本复杂性。
3 二维有界线性凸区域表示及误差区域
二维平面R2上线性凸区域A由一组线性不等式规定:
aix+biy≤ci(i=1,2,……,k),
(7)
其矩阵形式为:
(8)
定义A={(x,y)∈R2:aix+biy≤ci(i=1,2,……,k)}。若存在一个正数M>0,使得对任意的(x,y)∈A,有|x|+|y|≤M,则称A有界。几何上它由k条边aix+biy=ci(i=1,2,……,k)围成的封闭有界区域。如图5所示。
为方便讨论,不妨假定(7) 式中每一个不等式都是独立的。即,任意删去一个不等式将得到另一个更大的区域。
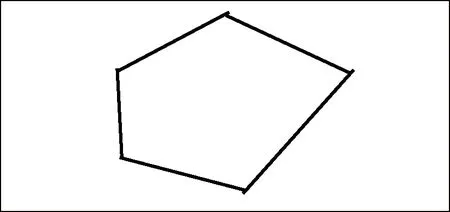
图5 封闭的有界凸区域Fig.5 Closed bounded convex region
形式上,一个轴对齐矩形r可以定义为:
r={(x,y)∈R2:a≤x≤b,c≤y≤d}(a 它对应一组不等式a≤x,x≤b,c≤y,y≤d。等价于 -x≤-a,x≤b,-y≤-c,y≤d, 统一到式(7)形式,其矩阵形式为: 给定平面R2一个分布D, 对于固定的0<ε<1,假定Pr(x,y)~D[A]>ε,则存在一个正向量(δ1,δ2,δ3,δ4)T(称为带宽向量)满足如下条件: (1)子矩形条件 (9) (2) 边界区域分段区域概率均分条件(对照图2中r1,r2,r3,r4) (10) Pr(x,y)~D[A1] =Pr(x,y)~D[A2]=Pr(x,y)~D[A3] =Pr(x,y)~D[A4]=ε/4。 (11) 概率均分在每个小区域上这主要是为了描述方便。其实,不必要求概率均分,只需4个正常数 为将方法延伸到一般凸区域。我们可能通过如下方法得到A1,A2,A3,A4。 以A1为例:A1对应约束条件 -x≤-a,带宽参数为δ1。 直线-x=-a“下移”δ1,得到新的约束条件:-x≤-a-δ1。其它约束条件不变,得到一个子区域: 边界段子区域A1=r-B1(原始矩形r减去 其它约束条件对应的子区域为: 边界区域是为误差分析设定的。 上述方法具有一般性,它是一般二维凸区域规定的目标概念学习的基础。 一般地,对于由(8)式定义的二维有界线性凸区域A, 在给定分布D下,假定Pr[A]>ε,必有正带宽向量(δ1,δ2,……,δk)T,满足条件: (12) 及k个子区域: (13) 其中ei=(0,…,0,1,0,…,0)T为k维单位向量中的i个向量。即,除第i个分量为1外,其余分量均为0。 设目标概念c:R2→{0,1}由二维平面R2上有界线性凸区域A规定。凸区域A由一组线性不等式给出:A={(x,y)∈R2:aix+biy≤ci(i=1,2,……,k)}。 假定在R2赋予一个分布D, 设S为容量为m独立同分布样本: S=(P1,……,Pm),Pj=(xj,yj)(1≤j≤m)。 PAC学习算法B: (1)输入凸区域A:aix+biy≤ci(i=1,2,……,k)},及样本 S=(P1,……,Pm)Pj=(xj,yj)(1≤j≤m); (2)对每个i=1,2,……,k,计算 (3)输出凸区域AS:aix+biy≤ci-di(i=1,2,……,k)}。 注:(1) 在算法B中,如果有样本点Pj=(xj,yj)落入区域A内部, 则对每个i,有di>0。 (2) 算法输出的凸区域AS是区域A内包含S中样本点的最小同型凸区域。这里同型指边界直线由原始区域边界直线平移得到(因为约束条件的系数矩阵不变)。 余下对算法的分析基本上与(轴对齐矩形概念)学习算法A的分析路径一致。 定理:二维欧氏空间上由有界结性凸区域定义的目标概念是有效PAC可学习的。 证明:含有k个约束条件的有界结性凸区域A可以由3k个参数(ai,bi,ci)(i=1,2,……,k)确定。因此,可以用3k来度量A的规模。由于k作为一个常数,独立于样本性和时间复杂性本质分析。因此,在分析时可以忽略。 可以看出:算法B的时间复杂性为O(m)。于是,分析的重点在样本复杂性m。 对于任意给定的误差参数0<ε<1,以及可靠性参数0<δ<1。 固定ε,对于任意给定的R2的分布D, 以及样本S=(P1,……,Pm),Pj=(xj,yj)(1≤j≤m)。类似轴对齐矩形概念的分析方法,不妨假设Pr[A]>ε。 对每一个固定的约束条件aix+biy≤ci,存在一个δi>0,满足条件(12)(13)。 在式(12)(13)中,令Ai=A-Bi,则A1∪……∪Ak构成A有内侧的一个ε/k-环带。如果对于任意的i有AS∩Ai≠∅,则由AS⊆A,我们有: er(A,AS)≤Pr[A1∪……∪Ak]≤Pr[A1]+……+Pr[Ak]=ε。 因此,在er(A,AS)>ε的假定下,至少存在某个i,使得AS∩Ai=∅。于是,对于来自独立同分布的取样样本S=(P1,……,Pm),我们有: PrS~Dm[er(A,AS)>ε] ≤PrS~Dm[∃(1≤i≤k):AS∩Ai=∅] (14) 因此,二维欧氏空间上由有界结性凸区域定义的目标概念是有效PAC可学习的。■ 文中的方法适用于数据集中的数据按预定凸区域聚类及误差分析,也可通过适当变换在非欧空间中讨论PAC学习算法。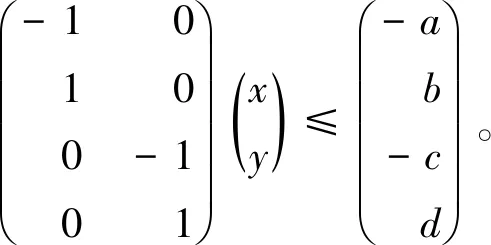
4 二维有界线性凸区域目标概念的PAC学习算法
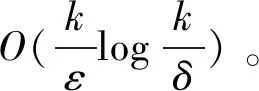
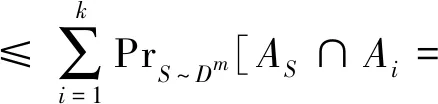
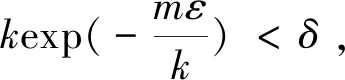
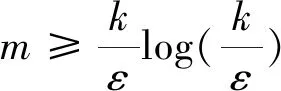
5 结语