大型客运站到发线运用计划优化编制

章 超 （兰州交通大学 交通运输学院，甘肃 兰州 730070）

1 概述

铁路通常由车站和车站之间的线路两大系统组成，在日常的组织运输生产的过程中，要保证两个系统的相互协调[1]。铁路大型客运站组织作业的质量、效率，直接影响该区域铁路甚至全路作业效率。如何根据列车运行图，合理地安排车站列车进路，确保车站到发线合理、高效的运用，是铁路大型客运站作业需解决的关键问题。车站到发线的运用计划是重中之重，影响列车是否能严格按照列车运行图运行。大多数研究主要以到发线的合理分配为优化目标，并没有考虑影响到发线分配的其它方面问题，比如咽喉区的作业交叉、旅客流量等因素。

在理论研究方面，T.Gainie[2]等通过时空网络法对列车进路的安排展开研究。Dorotea De[3]等利用图染色模型分析客运站到发线分配问题。Peter J.Zwaneved[4]等利用整数规划模型将进路分配问题描述为点包装问题，运用分支定界法求解问题。王正彬、杜文[5]等采用遗传算法求解客运站到发线运用计划模型。龙建成、高自有[6]等在建立车站衔接点的前提下，通过陈展网络法将车站进路问题进行描述，然后建立车站到发线需求的0-1规划模型，并运用模拟退火算法得出优化方案。吕红霞[7]等基于道岔组建立车站网状扑结构图，模型运用蚁群算法进行优化计算。在计算机辅助决策方面，毛节铭[8]、刘隽[9]等提出技术站智能调度决策系统的基本框架和组织思路，以期实现技术站生产指挥自动化。何瑞春[10]、杨信丰[11]等从铁路运输生产计划调度技术层面着手，展开相关研究工作。

车站运输生产效率能否提高，在于车站作业人员能否编制高水平、高效率的作业计划。实现车站到发线的合理分配，列车进路的合理安排，是铁路大型客运站应解决的重要问题。

2 大型客运站到发线运用计划优化原则

（1）任意一条到发线，已有列车占用时，不能继续向该到发线接入列车；任一列车，为其安排某条到发线后，不能再安排其他到发线。（2）如果必须要为先后到达两列列车安排相同到发线，要后续等待先行；如果是不同到发线，但进路存在冲突，也要后续等待先行。（3）车站在为到发列车安排进路时，应保证各条到发线的使用情况基本相同。（4）考虑旅客需求和固定使用到发线。（5）满足接发列车需要。

3 大型客运站到发线运用计划优化计算方法简述

对于大型客运站到发线的分配优化，很多著名专家学者做了深入的研究，提出了一系列的优化模型，比如到发线分配问题的图染色模型、0-1整数规划模型、多目标优化模型等，通过算法来进行求解，得出优化方案。计算方法主要有：遗传算法、分支定界法、启发式算法、弗洛伊德算法和排序算法等。这些研究配以计算机辅助系统，以减少人工工作量。

并不是所有车站都可以应用辅助系统获得到发线优化方案，需要通过一些简单的计算可得出一个相对可行的到发线优化方案。

3.1 基础数据。进行大型客运站到发线运用计划编制时，需要的理论数据有：车站平面布置图、列车运行图、到发线长度、列车进出站时运行速度等。

3.2 计算方法。提出针对大型客运站到发线运用计划优化问题的启发式算法：（1）通过分析车站平面布置图与列车运行图，得到列车到发信息表。（2）通过列车到发信息，确定对于在同一到发线作业的前行列车与后行列车之间或在不同到发线上作业但占用相同咽喉区道岔的两列列车进路之间是否存在冲突，得出进路冲突信息。（3）根据冲突进路长度和列车的进出站速度，得出存在进路冲突的两列列车之间占用进路的最小时间间隔。（4）根据最小时间间隔，得到到发线分配方案。

4 实例分析

以武广客运专线上的长沙南站为例，运用上述方法，得到一个可行的到发线分配方案。长沙南站平面布置示意图见图1。

武广客运专线上的长沙南站，是一个大型客运站，接发列车类型有始发、终到、通过、停站。长沙南站有两条正线，上行正线为VIII道，下行正线为IX道。14条到发线，其中1至7道为上行到发线；10至16道为下行到发线。

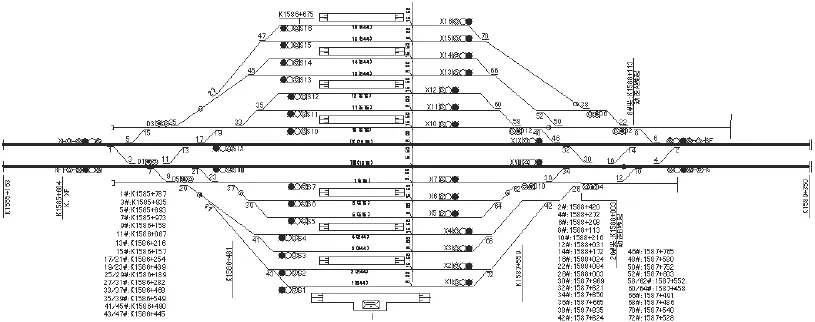
所有旅客列车的相关作业时间，都来自于武广客运专线列车时刻表。始发、终到列车由于要考虑旅客的乘降、乘务组换乘问题等需要在车站到发线上停留时间为20min。

本文研究认为所有道岔均为18号道岔，道岔号数较大，道岔的直向和侧向的距离近似相等，通过同一道岔直向和侧向的两条进路来说，可近似认为它们长度相等。列车进出站速度假设为40km/h，列车长度为240m。

（1）列车到发信息表。长沙南站14：00～16：00接发的列车信息，得到列车到发信息表，确定列车所要占用的到发线号数，从而确定列车接发车的具体进路，见表5。

（2）确定列车进路是否存在冲突。用一系列的道岔编号来表示列车进路，如上行列车接入到发线1的进路可表示为4、10、12、26、42、72。部分进路的某一部分可能会相同，产生重叠，即所谓的进路交叉。

将列车到发信息按照上下行方向分类，根据列车到发时刻以及各到发线所对应的接发车进路，确定各列车对应进路之间是否存在冲突。用列车到发信息表中列车的编号表示相对应的列车进路。所对应的进路冲突如表1、表2所示。

从表1和表2中得出，上行方向，G1010与G1124次列车接车进路、发车进路之间存在冲突，同样G1132与G732次列车之间、G79与G1133次列车之间也存在冲突。

（3）确定冲突进路的具体冲突位置。对于表1和表2得出具有冲突的三对列车进路，参考进路冲突的具体位置，求出冲突进路的长度，然后运用公式得出冲突进路解锁需要的最短时间。冲突进路位置表见表3。

表3中，冲突进路的第一行表示的是在接车进路上的冲突，第二行表示在发车进路上的冲突，解锁时间为先行列车解除占用这段进路的时间，也就是后续列车能够开始占用进路的最早时间。

（4）综合上述各种条件，以及求出的各种数据，得出列车占用车站咽喉区以及到发线的具体时间顺序，即进路分配情况见表4。

从表4中，可以具体地看到：列车占用车站咽喉、到发线的顺序以及确切的时间，具有冲突进路的相邻两列车之间的接续时间。获得列车进路具体时间见表5。

5 结束语

针对无法应用辅助系统获得到发线优化方案的车站，依据进路分配问题的整数线性规划模型提出一种计算方法，以武广客运专线上的长沙南站为实例，对到发线的运用计划进行优化，得出一个可行的到发线分配方案。该研究方法只考虑主要影响因素，并没考虑列车晚点、线路设备工作状态等对列车运行的影响。如何在满足各影响因素的同时，又不依赖系统简单有效地获得一个更符合现场实际工作的到发线分配方案，提高车站的通过能力和工作效率仍有待深入研究。

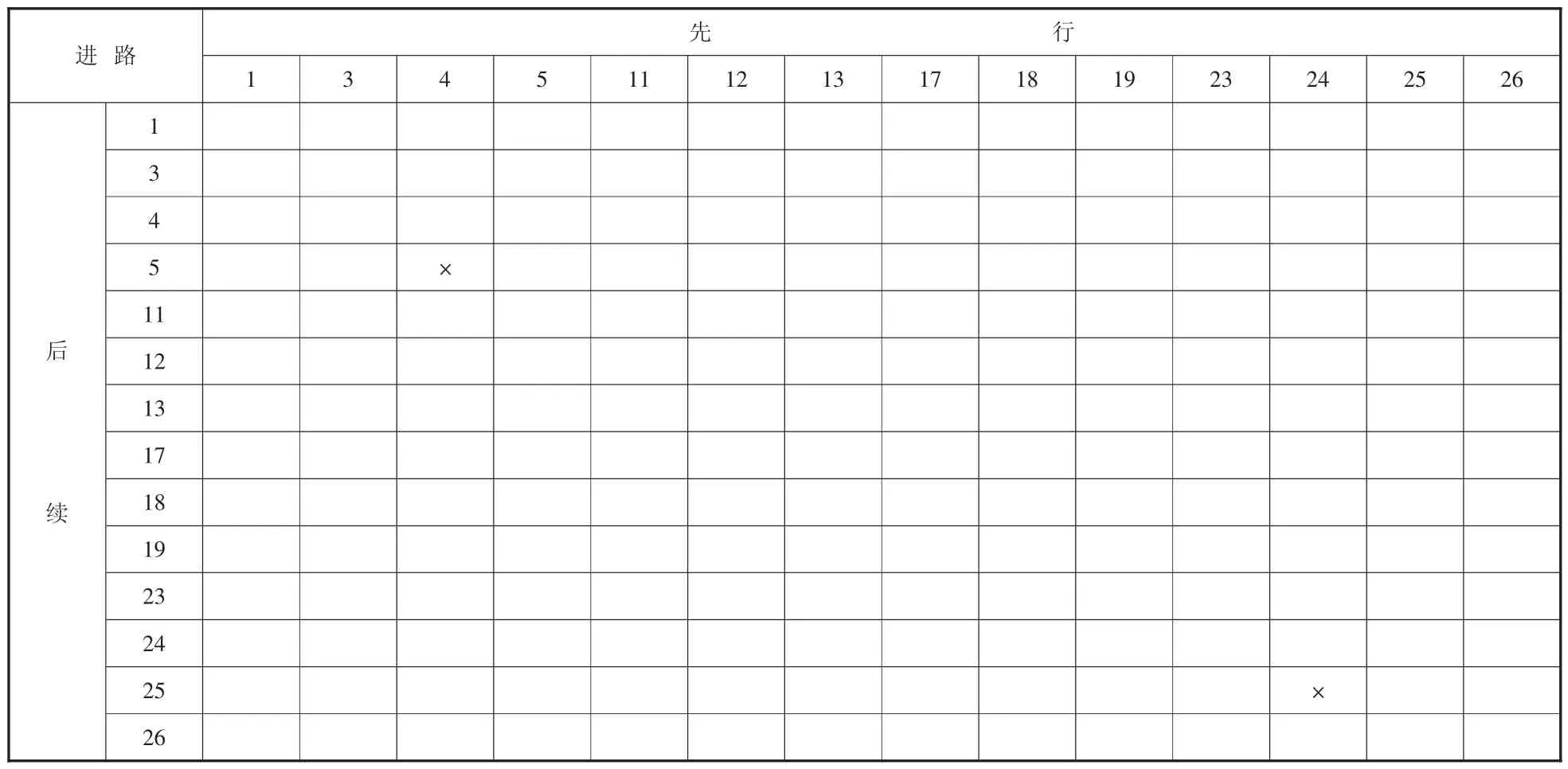
表1 上行列车进路冲突表

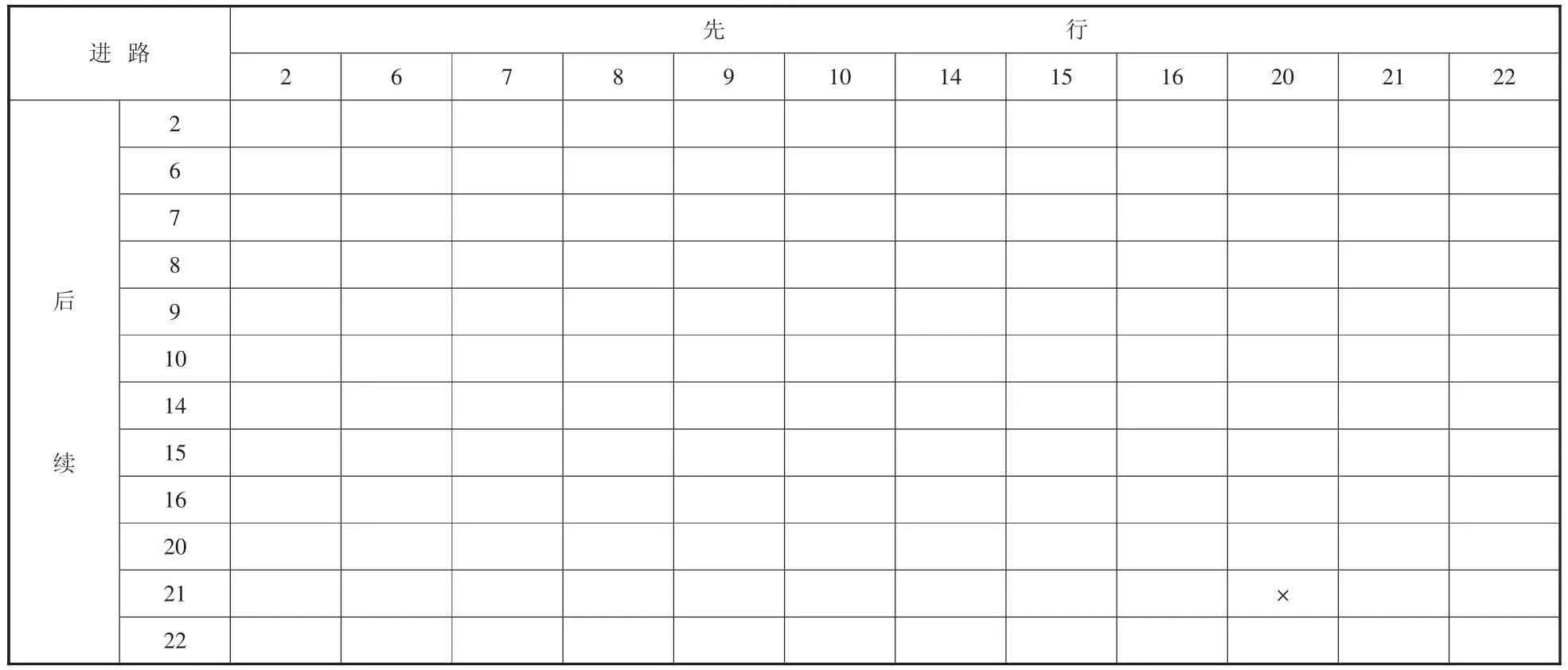
表2 下行列车进路冲突表

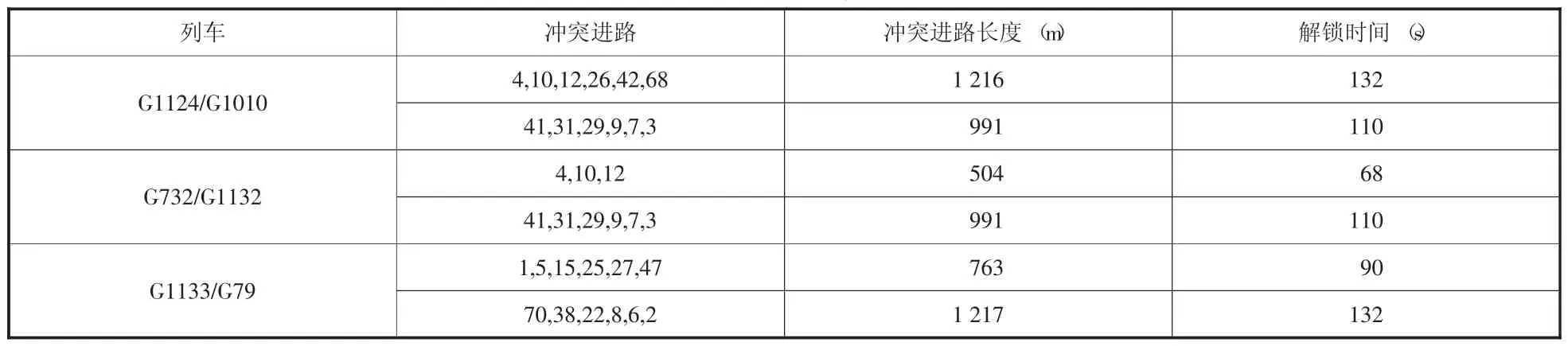
表3 冲突进路位置表

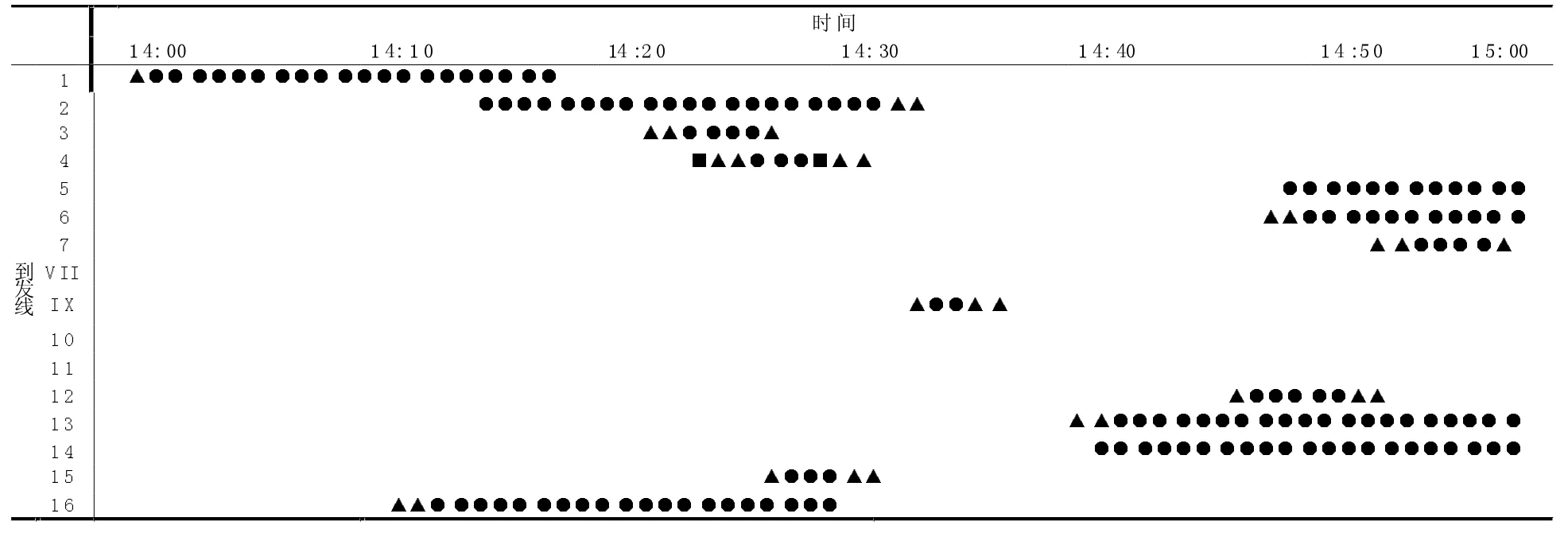
表4 进路分配表

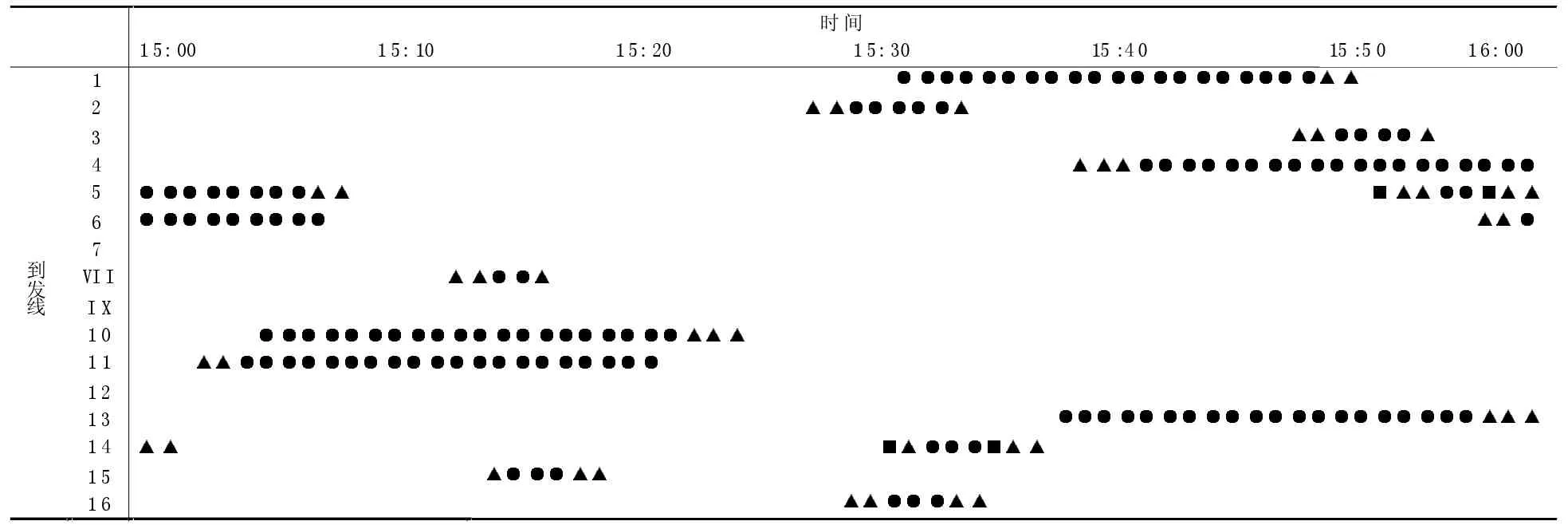
续表4 进路分配表

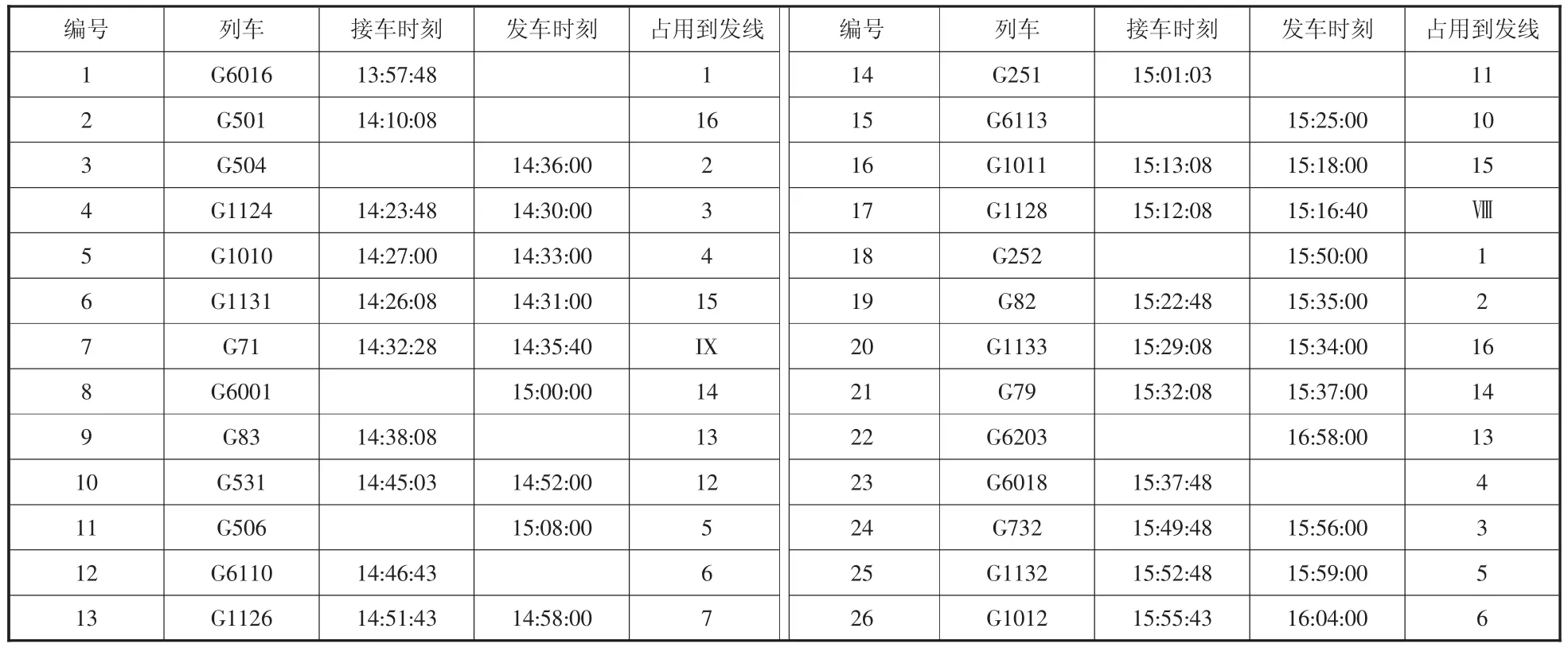
表5 列车进路具体时间