直齿轮纯扭转模型弹性动力学分析
郑钰馨, 奚 鹰, 袁 浪, 卜王辉
(同济大学 机械与能源工程学院, 上海 201804)
高速度、高精度和高承载能力的高性能机械系统,对齿轮的传动性能提出了更高的要求,如RV减速器作为高精度工业机器人用减速器,其传动精度要求不大于1′,所以其制造安装要求、传动平稳性要求和振动噪声要求都大幅提高.车辆系统的齿轮传动装置,在长时间的使用中和高温、高速、恶劣环境中,其传动性能直接影响了驾驶人和乘客的乘坐体验.直齿轮是齿轮传动形式的基础,对其他齿轮传动形式的研究都要由此展开,所以对直齿轮动力性能的研究很有必要.
文献[1]采用增量谐波平衡法对气动弹性系统进行分岔分析.文献[2]针对传统增量谐波平衡法求解多频激励局部非线性系统周期响应耗时太长的问题,提出了降维增量谐波平衡方法.文献[3]在采用谐波平衡法对复合行星系统求解基频稳态响应的基础上,采用Gill积分法对系统的平移-扭转模型进行了动力学求解.文献[4]建立了3自由度齿轮传动模型,采用Runge-Kutta法对方程进行了求解.文献[5-7]提出用数值方法分析纯扭转齿轮在不同参数下的运动状态变化过程,考虑非线性因素,提出时变啮合刚度、齿侧间隙变化和综合误差对系统动态响应影响较大的结论.文献[8]建立含有齿侧间隙和内部激励误差的平动-扭转运动动力学方程,采用谐波平衡法和数值法讨论了多间隙和单间隙对系统动力学特性的影响.文献[9]对行星齿轮动力学的振动研究历史进行了总结和回顾.通过文献研究发现,齿轮动力学方程主要通过解析和数值两种方法求解,但解析法求解过程复杂,能求解的方程较为简单,而数值法求解迅速并且可以求解复杂方程.使用数值法更加适合非线性特性分析,但是现有研究中,齿轮动力学非线性特性分析主要停留在定性分析阶段,定量分析较少,并且定量分析中的参数设置复杂,要根据多种算法才能最终确定一个最佳参数,而现有文献几乎忽略了参数设置的合理性研究;同时,在非线性分析中,缺少多种非线性因素耦合影响分析.
本文建立了4自由度的直齿轮纯扭转振动模型,先在不考虑原动机负载转动特性和其他非线性因素的影响下,求解了系统的动态响应曲线和频率曲线,后从定性和定量两个方面讨论了在啮合误差、时变啮合刚度和啮合间隙非线性因素影响下的系统动态特性变化规律,以及考察了单个和多个因素对系统非线性动力学特性的影响,形成了一套完整的直齿轮非线性特性分析方法.
1 直齿轮纯扭转振动模型
1.1 不考虑非线性因素的纯扭转振动模型
建立仅考虑传动轴扭转刚度和啮合刚度的4自由度1∶1传动的齿轮-转子扭转振动模型,如图1所示.其中:kv为主动轮1和从动轮2之间的啮合刚度;cv为主动轮1和从动轮之间的啮合阻尼;e(t)为主动轮1和从动轮2之间的啮合误差.
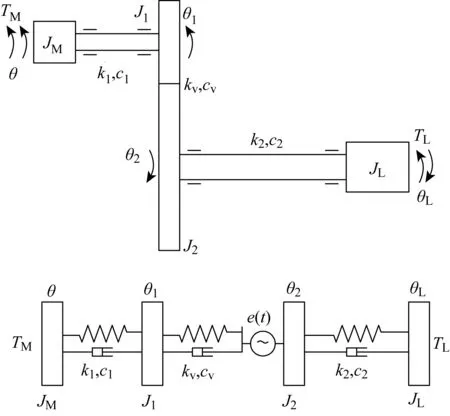
图1 直齿轮纯扭转振动模型Fig.1 Pure torsional vibration model of spur gear
取θ、θL、θ1、θ2为系统的广义坐标,用牛顿-欧拉方法建立系统的动力学方程为
式中:θ为原动机转角;θ1为主动轮1的转角;θ2为从动轮2的转角;θL为负载转角;JM为原动机转动惯量;J1为主动轮1转动惯量;J2为从动轮2转动惯量;JL为负载转动惯量;c1为输入轴的扭转阻尼;c2为输出轴的扭转阻尼;k1为输入轴的扭转刚度;k2为输出轴的扭转刚度;TM为原动机驱动转矩;TL为负载转矩;r1为主动轮1半径;r2为从动轮2半径;F为齿轮啮合力.
当假设原动机等速回转时,则原动机的θ不作为广义坐标,而作为已知量.取广义坐标为
φ1=θ1-θ
(5)
x=r1θ1-r2θ2
(6)
φ2=θL-θ2
(7)
式中:x为啮合线上两齿轮的相对位移;φ1、φ2分别为主、从动轴的扭转角.
通过坐标变换,消除了齿轮啮合间的刚体位移,并将自由度从4变成了3,简化了系统运算.
1.2 不考虑非线性因素的纯扭转振动模型求解结果
1.2.1转角 通过计算得到如图2(a)所示的系统转角随时间变化的曲线.由于系统传动比为1∶1,所以原动机、齿轮1、齿轮2和负载的转角基本相同,但由于轴的扭转刚度、齿轮啮合刚度以及非线性因素的影响,转角存在一些微小的差异,如图2(b)所示.由于输入轴转速假设为恒定值500 r/min,则在300 s内,转过9×105度,图2说明模型动力学方程的建立和求解是正确的.
1.2.2系统动力学响应 选取啮合线上两齿轮的相对位移即齿轮之间的线性传动误差作为考察量.由图3(a)可见,啮合相对位移在经过一定时间的振荡后逐渐趋于平稳,频谱分析图3(b)上只有一个谱峰 0.059 38 Hz.

图2 原动机、齿轮1、齿轮2和负载的转角Fig.2 Rotation angles of prime motor, gear 1, gear 2 and load
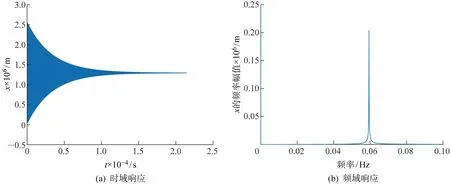
图3 不考虑非线性因素的纯扭转振动模型响应结果Fig.3 Result of the pure torsional vibration model without considering nonlinear factors
1.3 考虑直齿轮齿间间隙、时变啮合刚度和啮合误差时纯扭转振动模型
1.3.1非线性因素表达 当考虑齿间间隙、时变啮合刚度和啮合误差的时候,两个齿轮之间的啮合力为
(8)
式中:xq(t)为齿间非线性总间隙;kv(t)为齿间时变啮合刚度.
xq(t)的表达式为

(9)
xp=r1θ1-r2θ2-e(t)
(10)
式中:xp为考虑齿间啮合误差时候的齿间变形;b为齿间间隙的1/2.
齿间啮合误差的表达式为
(11)
式中:ej为啮合误差第j阶对应的幅值;φej为啮合误差第j阶对应的相位;ωm为与啮频对应的圆频率;n为最高阶数.
啮频fm为轴的转动频率和齿数的乘积[10]:
(12)
式中:n1为齿轮1的转速;n2为齿轮2的转速;z1为齿轮1的齿数;z2为齿轮2的齿数.取j=1,此时一阶齿间啮合误差激励中的e1=10 μm,φe1=0.
直齿轮外啮合时变刚度kv(t)可以表示为平均值kv和随时间变动量Δkv(t)的叠加:
kv(t)=kv+Δkv(t)
(13)
(14)
式中:ki为时变啮合刚度第i阶对应的幅值;φki为时变啮合刚度第i阶对应的相位;n′为最高阶数.
A0=2Δ(2ε-1),
(15)
(16)

图4 考虑非线性因素的系统动态特性Fig.4 System dynamic characteristic considering nonlinear factors
式中:Δ为时变刚度的最大刚度值和最小刚度值之间差值的一半;ε为齿轮端面重合度.取i=1,此时一阶齿间啮合刚度中的ε=1.65,Δ=0.25,n′=1,φk1=0.

(17)
(18)
(19)
式中:ωd为时间标称尺度;bd为位移标称尺度.
(20)

(21)
(22)

1.3.2系统动力学响应 图4所示为考虑非线性因素时系统的动态特性,可见时域和频域都发生了明显变化.由于非线性因素的存在,齿轮啮合线性传动误差加大,频率由于外界激励的存在,由 0.059 38 Hz变为 0.013 05 Hz,同时在其他频率上激起了微小的振动,不过不影响整体动态性能.
2 系统非线性动力学特性分析
2.1 定性分析
常用非线性分析方法主要有时间历程、相图、Poincáre截面、功率谱和分岔图等[10].
时间历程可以反映系统的振动形态,但是由于其长周期性以及多种运动成分之间很难区分,所反映的动态特性有限.
相图通常采用某物理量的位移和速度的时间历程共同绘制出平面图形.周期运动的相线为一条闭合曲线;拟周期运动的相线表现出一定的带状规律性曲线;混沌运动的相线则相互交叉缠绕,并且充满于相空间中的一部分.
Poincáre截面对于非自治系统,采用频闪法,即按照激励周期取间隔状态位移和速度的值,并将其绘制在平面中.在Poincáre映射图中,系统的周期运动表现为有限个离散点;拟周期运动表现为若干条封闭曲线;混沌运动表现为一个具有分形结构的杂乱点集.
功率谱反映了信号中各频率成分的功率.若系统是周期运动,功率谱为离散的分立谱峰;拟周期运动的功率谱为由若干个不可公约的基频以及这些基频线性组合形成的尖峰;混沌运动,则会出现噪声背景和较宽的连续频谱.
分岔是当系统某一参数达到一定值,系统的性质将会突然发生改变.系统处于周期运动时,分岔图上为1条或数条随参数变化的曲线;系统处于混沌运动状态时,分岔图上同一参数对应多个响应值,从而随参数变化形成一段点状带.分岔图不能完全区分混沌运动和拟周期运动.
2.2 定量分析
最大Lyapunov指数、分形维数是非线性动态特性定量分析的重要工具[10].
Lyapunov指数是相空间内相邻轨迹的平均指数发散率的数值特征.最大Lyapunov指数λ<0,对应于稳定的不动点和周期运动;λ>0,对应于混沌运动;λ=0的点必为分叉点.
分形维数指非线性变化下的不变性,说明了吸引子中的密集程度或刻画它所必需的信息量,可以是整数也可以不是整数.关联维作为分形维数的一种,主要描述了状态变量随时间变化前后的关联性.
2.3 最大Lyapunov指数计算方法和步骤
2.3.1计算最大Lyapunov指数方法 最大Lyapunov指数的计算方法主要有:由定义法延伸的Nicolis方法、Jacobian方法、Wolf方法、P-范数方法和小数据量方法[10].
如果系统较为简单,采用定义法和Jacobian方法;如果系统方程比较复杂,如超维系统,或者为一时间序列,采用Wolf方法和小数据量方法;P-范数方法较少采用.
Wolf方法和小数据量方法都要对时间序列进行重构相空间,重构相空间的优良取决于嵌入维数m和时间延迟τ.
2.3.2C-C法和复自相关法求τ以及估算m求τ的方法主要有C-C方法和复自相关法:C-C方法是统计经验方法;复自相关法是自相关法和平均位移法的综合.
根据C-C方法的结果对τ和m进行初步判定。首先求出对应不同τ情况下的时间序列的关联积分的平均值Smean,再计算时间序列的关联积分最大值和最小值之间的差值ΔS(τ),最后根据Scor(τ)=Smean+ΔS(τ)求出最终的时间序列关联积分Scor(τ),如图5所示,根据ΔS(τ)的第一个极小值确定时间序列独立的第一个局部最大值并作为延迟时间τ;根据Scor(τ)的最小值确定时间序列独立的第一个整体最大值延迟时间窗口τw,τw=(m-1)τ,由图5初步判定延迟时间τ=15 s,最大延迟时间窗口τw=40 s,窗口嵌入维数计算值为m=4。
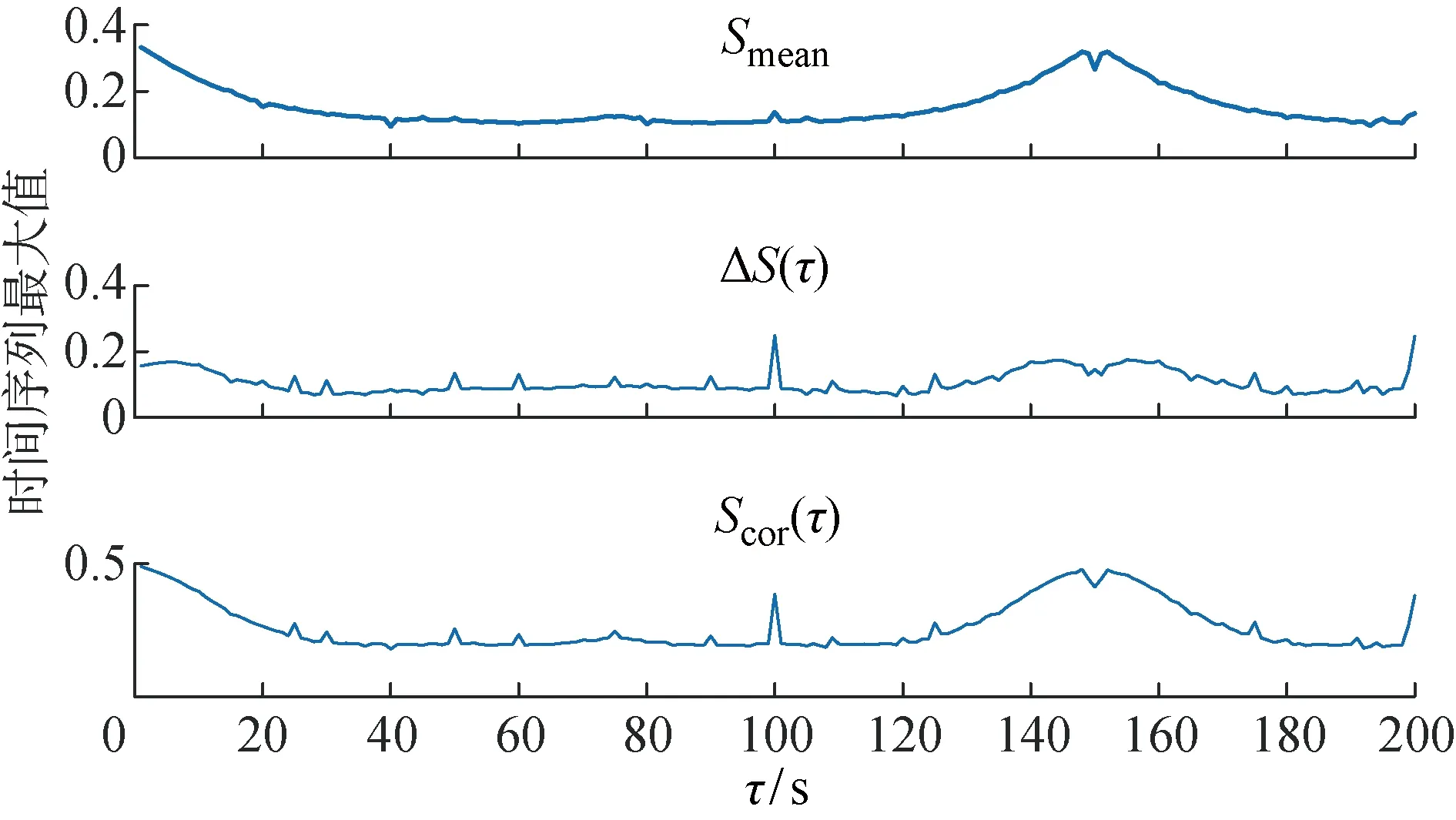
图5 C-C法求延迟时间Fig.5 C-C method to get the delay time
采用复自相关法,得到如图6所示的结果,Cτ为延迟时间下对应的位移.假设m=4,时间序列的最大延迟时间为27 s.结合图5可得,最大延迟时间窗口为40 s,当最大延迟时间为27 s时,最小嵌入维数为3.

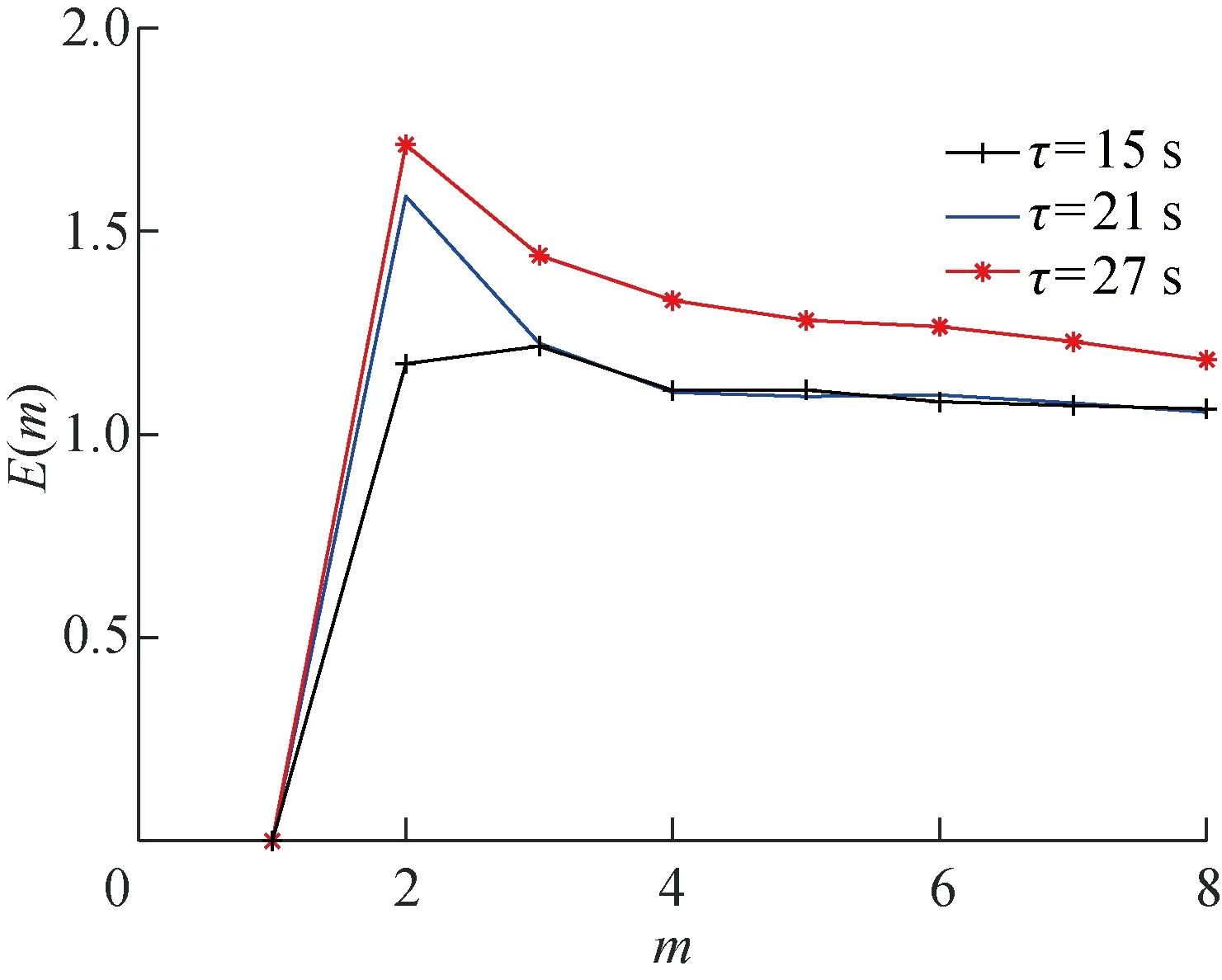
图6 复自相关法求延迟时间Fig.6 Multiple-autocorrelation method to get the delay time
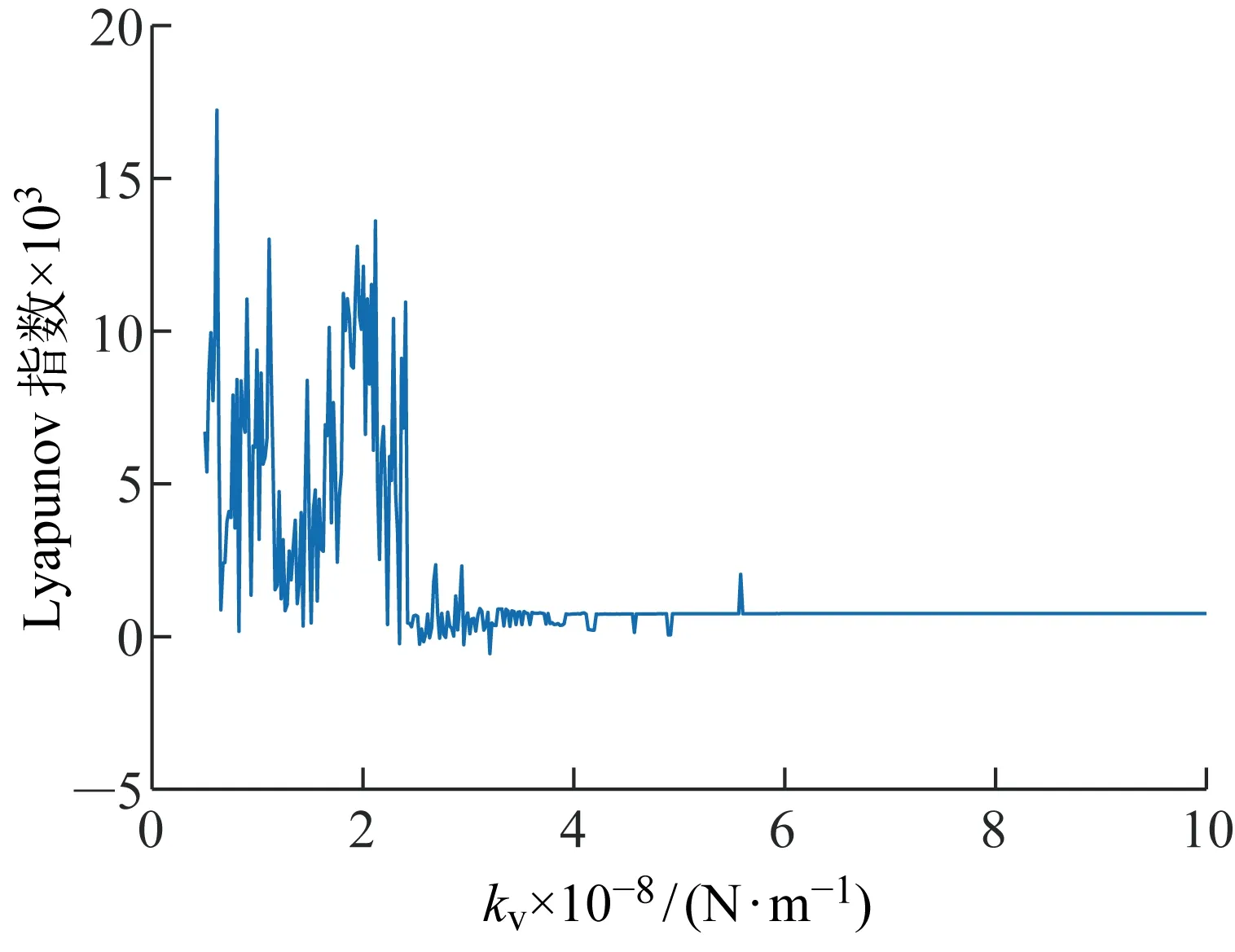
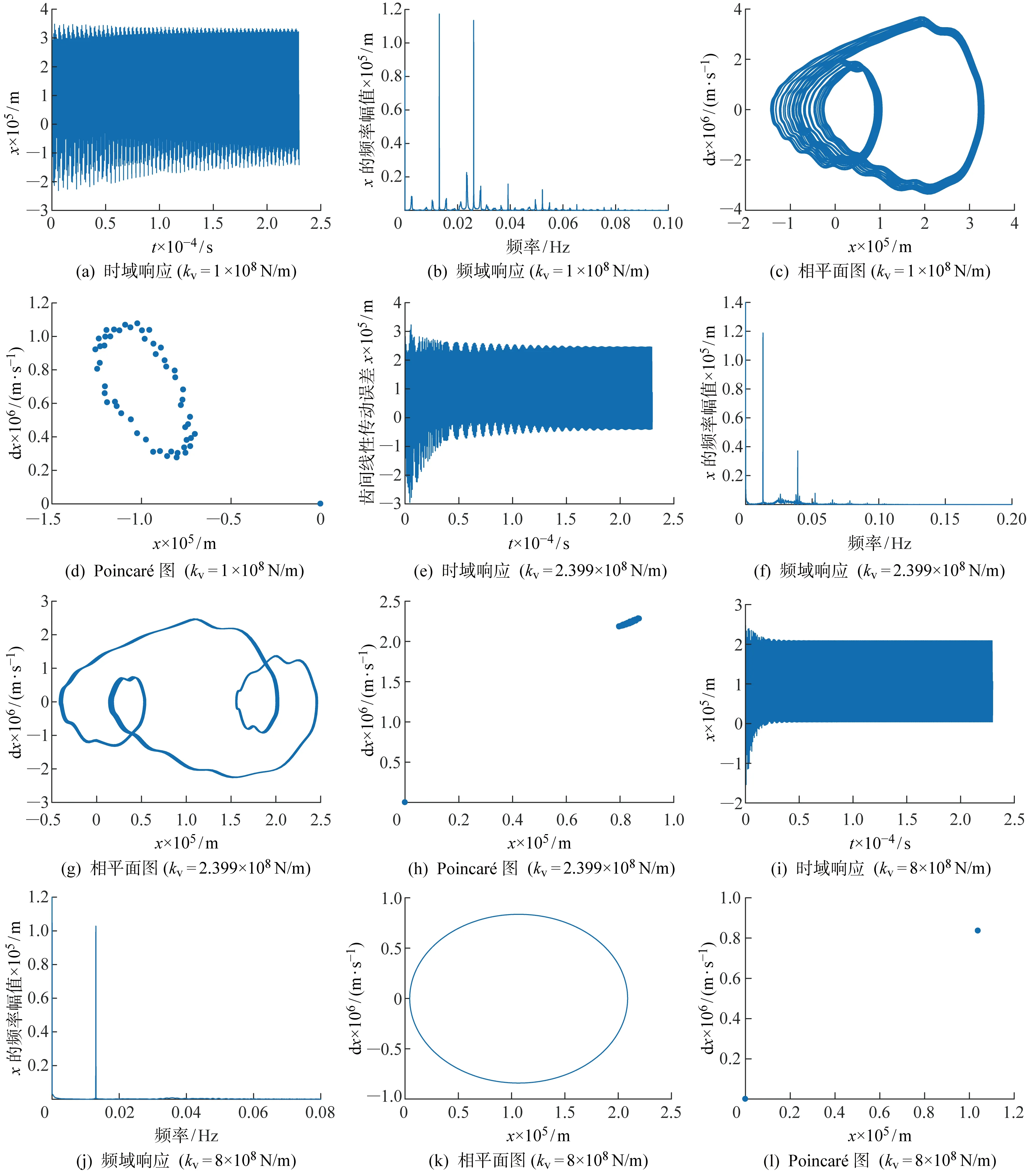
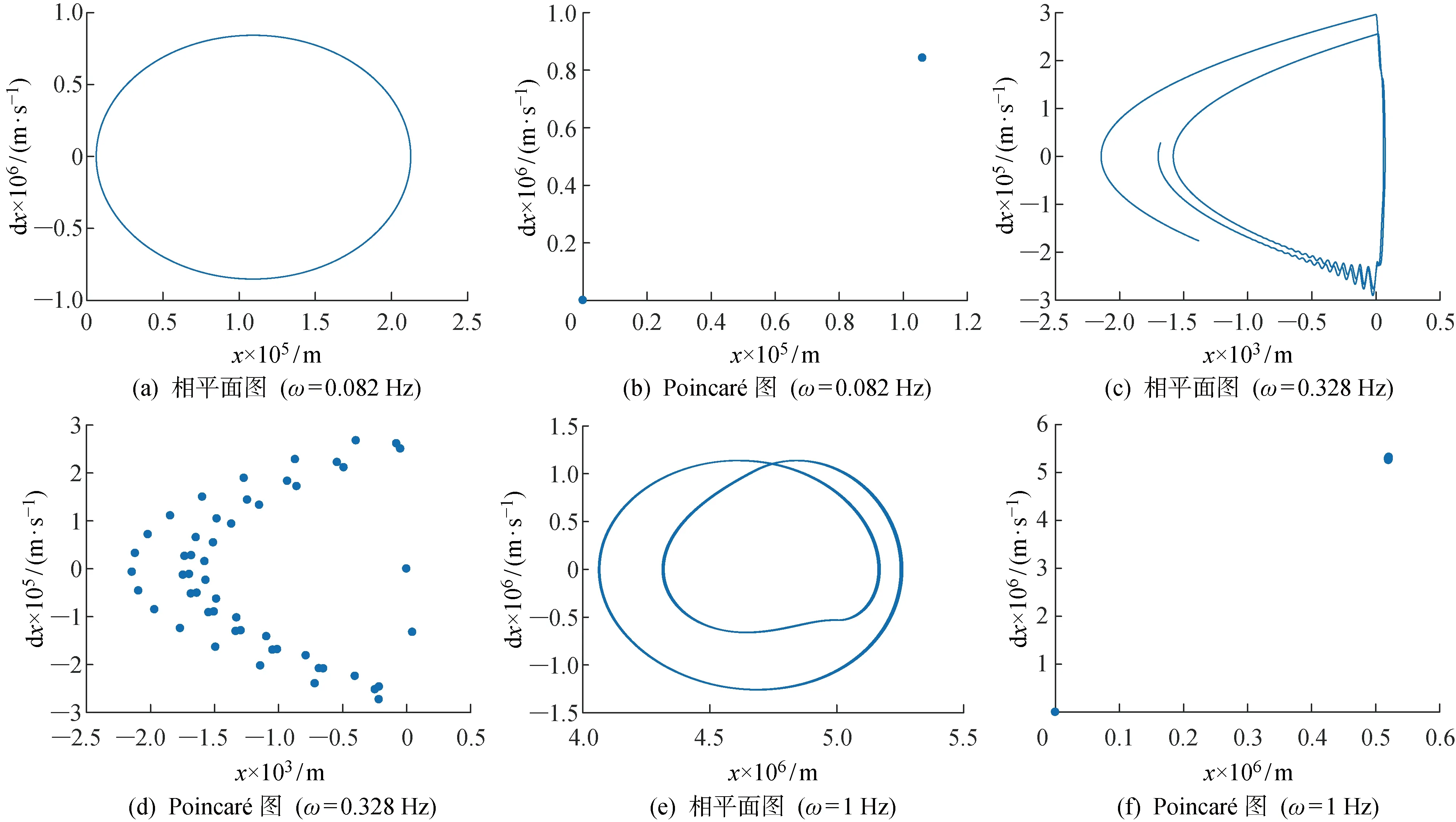
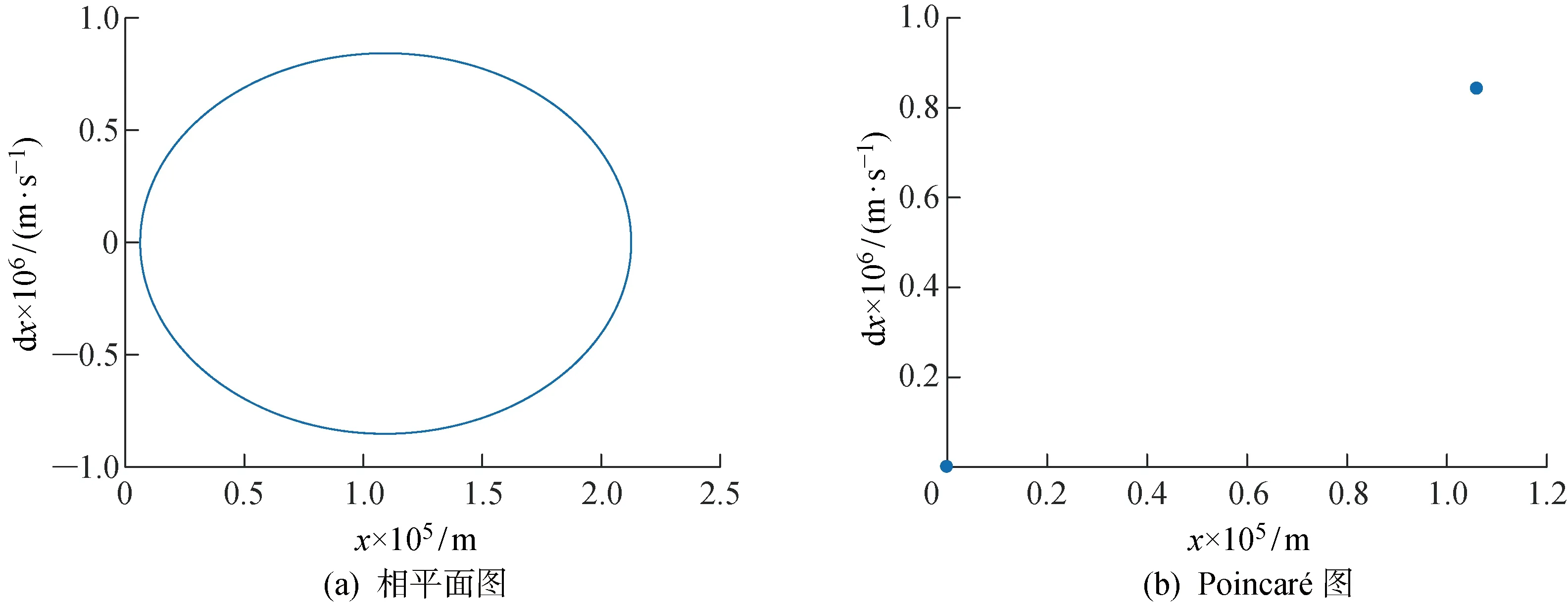
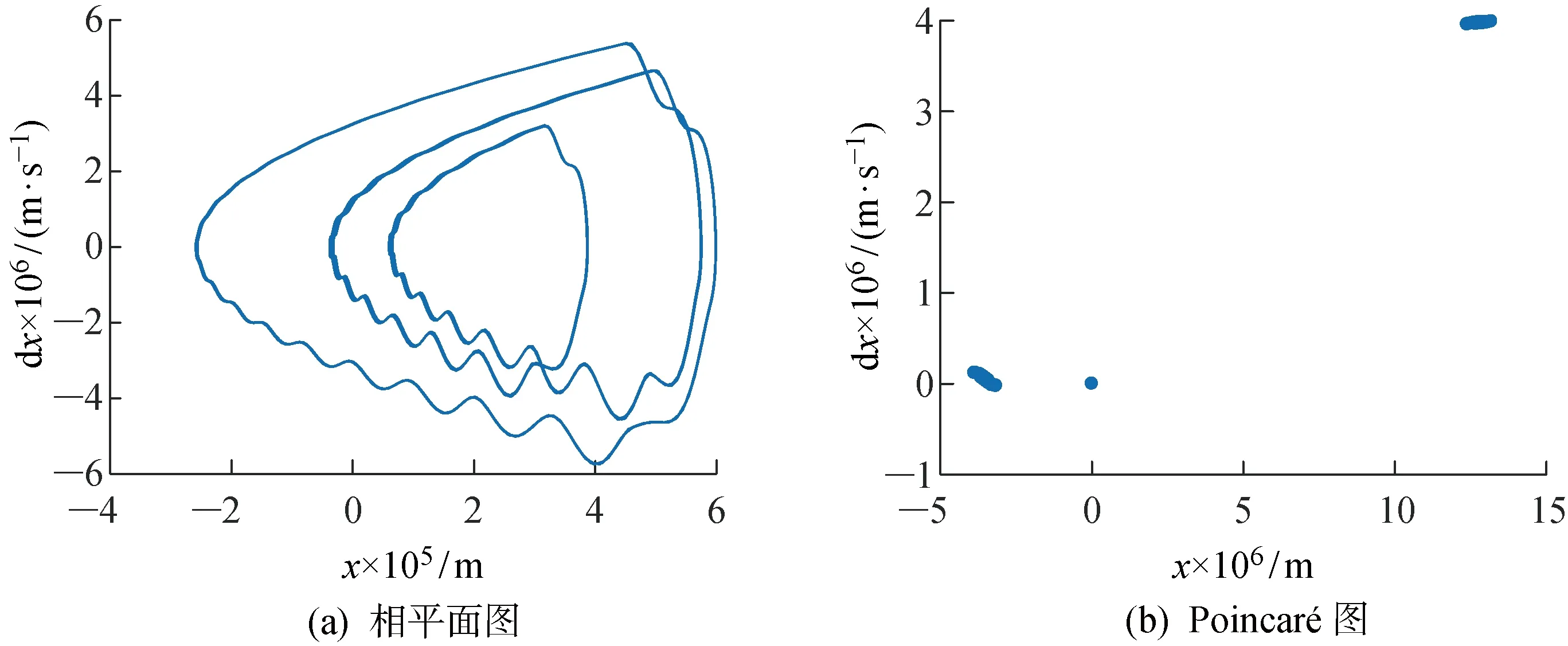
2.3.3G-P算法和Cao法求mG-P算法中首先计算出序列的关联维数d,然后利用嵌入维数m≥2d+1,选取合适的嵌入维数.初选嵌入维数2≤m≤20,对于尺度Rr在[-6,0]范围内,吸引子关联维数d与累积分布函数C(Rr)满足对数线性关系.根据图7,拟合段的斜率即关联维数1 图7 G-P算法计算序列的关联维数Fig.7 G-P algorithm to calculate the correlation dimension of the sequence Cao法对原始的虚假邻点法中的m的判定方法从主观判断变为定义新的变量E(m),当m大于某个特定值后m0,E(m)不再变化,此时m0即是最小嵌入维数.根据图8,尽管延迟时间不同,但到m=4之后,E(m)基本不再变化,所以,m=4是时间序列的最小嵌入维数. 图8 Cao算法求解最小嵌入维数Fig.8 Cao algorithm to solve the minimum embedding dimension 综上所述,根据C-C方法、G-P算法和Cao法综合选择m=4为系统时间序列的嵌入维数,根据 C-C 方法、复自相关法和Cao法综合选择τ=15 s为系统时间序列的延迟时间.将m和τ代入Wolf方法和小数据量方法中,即可求得时间序列的最大 Lyapunov 指数. 齿轮啮合刚度在5×107~1×109N/m之间时,系统的分岔图如图9所示,系统最大Lyapunov指数如图10所示.可以看出kV在5×107~2.399×108N/m之间时,系统混沌运动严重;在 2.399×108~5.583×108N/m之间为混沌和拟周期交互的运动状态,此段混沌程度较 2.399×108N/m之前区域低很多;从 5.583×108N/m之后,最大Lyapunov指数收敛于0, 但不小于0, 说明系统进入准周期或者倍周期运动,但并没有进入严格周期运动,并且此时系统并不处于稳定状态,其他参数的改变可能会导致系统失稳. 图9 随啮合刚度变化的系统分岔图Fig.9 System’s bifurcation diagram with vary- ing meshing stiffnesses 图10 随啮合刚度变化的系统最大Lyapunov指数Fig.10 Maximum Lyapunov exponent of system with varying meshing stiffnesses 图11所示为不同啮合刚度下非线性特性图.当齿轮啮合刚度为1×108N/m时,相平面图(图11(c))为充满一定空间的相互交错曲线,Poincaré图(图11(d))是具有一定云状的点集,频谱图(图11(b))出现了噪声背景和宽峰的连续谱,此时处于混沌状态.当齿轮啮合刚度为 2.399×108N/m时,相平面图(图11(g))为具有一定宽度的闭合曲线带,此时系统出现左右两个中心区域,并在两定点之间做稳定重复的运动,此时,Poincaré图(图11(h))为一封闭曲线,频率图(图11(f))由不可通约的频率组成,在组合频率处出现不可公约的谐波分量,所以此时系统为拟周期运动.当齿轮啮合刚度为 5.583×108N/m时,系统最后一次做两定点的拟周期运动, 之后系统进入了相对稳定周期为1的准周期运动,如图11(j)、(k)和(l)所示,并且通过图11(a)、(e)和(i)可知,随着啮合刚度的增加,齿轮之间的线性传动误差减小,振动响应趋于平稳.综上,齿间啮合刚度取较大值有利于齿轮传动. 图11 不同啮合刚度下非线性特性图Fig.11 System’s nonlinear characteristics with different meshing stiffness 图14 不同啮合频率下非线性特性图Fig.14 System nonlinear characteristic with different meshing frequencies 电机转速额定转速为2 000 r/min,此时无量纲下啮合频率为 0.328 Hz;最大转速为 3 000 r/min,啮合频率为 0.492 Hz;部分型号电机最大转速为 5 000 r/min,啮合频率为 0.820 Hz.由图12和图13可知,当啮合频率w=0~0.086 3 Hz时,最大Lyapunov指数维持在 0.000 7,接近0,根据图14(a)和(b)可知,此时系统维持在周期为1的准周期状态.当w=0.086 3~0.995 3 Hz时,系统进入混沌运动状态,如图14(c)和(d)所示,其中个别频率出现周期运动.当w=0.995 3~1.106 5 Hz时是周期运动状态,如图14(e)和(f)所示,1.106 5 Hz之后又出现混沌运动.由于w=0.086 3~0.995 3 Hz时,系统基本为混沌运动,在进行系统传动误差实验时,不宜采用此区间的速度, 并结合当前机械传动实验中扭矩传感器和角度编码器等测量仪器使用速度范围限定的要求,采用低速进行传动实验是合理的. 图12 随啮合频率变化的系统分岔图Fig.12 System’s bifurcation diagram with varying meshing frequencies 图13 随啮合频率变化的系统最大Lyapunov指数Fig.13 Maximum Lyapunov exponent of the system with varying meshing frequencies 当齿轮啮合间隙b=0~100 μm时,系统分岔图如图15所示,系统最大Lyapunov指数如图16所示.当b=0~13.11 μm时为准周期运动和周期为1的运动状态,如图17所示;当b=13.11~28.53 μm,经过倍周期分岔变成周期为2的运动状态,如图18所示;b=28.53~39.14 μm 为1周期和2周期交互状态;b=39.14~45.95 μm为3周期状态,如图19所示;b=45.95~58.36 μm为1周期、 2周期和3周期交互状态;b=58.36 μm之后为混沌运动,如图20所示.综上,在保证能够容纳一定润滑油的情况下,齿轮啮合间隙不要超过 58.36 μm. 图15 随啮合间隙变化的系统分岔图Fig.15 System’s bifurcation diagram with varying meshing clearances 图16 随啮合间隙变化的系统最大Lyapunov指数Fig.16 Maximum Lyapunov exponent of the system with varying meshing clearances 图17 b=10 μm时的非线性特性图Fig.17 System’s nonlinear characteristics when b=10 μm 图18 b=20 μm时的非线性特性图Fig.18 System’s nonlinear characteristics when b=20 μm 图19 b=40 μm时的非线性特性图Fig.19 System’s nonlinear characteristics when b=40 μm 图20 b=60 μm时的非线性特性图Fig.20 System’s nonlinear characteristics when b=60 μm 通过单非线性因素分析,能够确定系统处于周期、准周期还是混沌运动,要尽量避免系统处于混沌运动状态.在多因素耦合分析时,选择啮合刚度为 3×108~8×108N/m,啮合间隙为1~50 μm,尽量避开混沌运动状态.根据图21和图22可知,齿轮啮合线性传动误差随着啮合间隙的增加而出现阶段性的增大,随着啮合刚度的增加变化幅度不大,但间隙为9 μm,刚度大于 6.889×108N/m时,系统振幅明显增加,当间隙为 48.52 μm,刚度小于 3.707×108N/m时,振幅也有明显突变,系统应尽量避免处于这2种参数配置下.此外,系统要严格控制啮合间隙,在保证一定的润滑程度下,尽量减小啮合间隙保证系统的稳定运行. 图21 啮合刚度和啮合间隙对系统非线性特性影响三维图Fig.21 The 3D graph of the meshing stiffness and meshing clearance influence on the nonlinear characteristics of the system 图22 啮合刚度和啮合间隙对系统非线性特性影响云图Fig.22 The 2D graph of the meshing stiffness and mesh-ing clearance influence on the nonlinear characteristics of the system 选择无量纲啮合频率为 0.001~0.820 Hz,包含电机转速0~5 000 r/min的范围.由图23和24可知,在啮合频率小于 0.092 Hz时,齿轮啮合线性传动误差基本没有变化, 但当大于 0.092 Hz时,齿轮啮合线性传动误差随着啮合频率的增加而逐渐减小,随着啮合刚度的增加变化幅度不大, 所以系统在做传动误差等实验时应尽量保持在低转速下进行,并且高转速时系统振动振幅加大,影响系统中零部件的工作特性和使用寿命,所以要避免系统长期处于高速运行状态. 图23 啮合刚度和啮合频率对系统非线性特性影响三维图Fig.23 The 3D graph of the meshing stiffness and mesh-ing frequency influence on the nonlinear charac-teristics of the system 图24 啮合刚度和啮合频率对系统非线性特性影响云图Fig.24 The 2D graph of the meshing stiffness and mesh-ing frequency influence on the nonlinear characteristics of the system 根据图25和图26可知,在啮合频率小于 0.108 5 Hz时,齿轮啮合线性传动误差基本没有变化,但当大于 0.108 5 Hz时,齿轮啮合线性传动误差随着啮合频率的增加而逐渐减小,随着啮合间隙的增加变化幅度不大,说明在保持一定啮合速度的情况下,间隙对振幅的影响较小.综上,啮合频率是对系统非线性特性影响最明显的因素,啮合间隙其次,影响较小的是啮合刚度,在保持一定齿面硬度的情况下,尽量保持较小啮合间隙和啮合频率能够有效减小振动幅度. 图25 啮合间隙和啮合频率对系统非线性特性影响三维图Fig.25 The 3D graph of the meshing clearance and mesh-ing frequency influence on the nonlinear charac-teristics of the system 图26 啮合间隙和啮合频率对系统非线性特性影响云图Fig.26 The 2D graph of the meshing clearance and mesh-ing frequency influence on the nonlinear characteristics of the system (1) 从时域和频域两个方面得到了系统动态响应,从定性和定量两个角度进行了系统非线性特性影响分析,建立了一套较为完整的齿轮系统动力学特性分析方法.在此基础上,对系统中的各种非线性因素进行合理匹配、把控和验证,能够得到具有优良动力学性能的传动系统. (2) 在非线性特性定量分析中,嵌入维数m和时间延迟τ直接影响最大Lyapunov指数图的绘制,要通过C-C方法和复自相关法估算m和τ,再根据G-P算法、Cao法确定最终的m和τ,通过多种方法的综合判断才能保证这两个参数取值的合理性. (3) 在单非线性因素分析中,当啮合刚度大于 5.583×108N/m时,系统进入较为稳定的准周期状态,啮合频率在 0.086 3~0.995 3 Hz之间时,系统基本为混沌状态,啮合间隙大于 58.36 μm时,系统进入混沌状态.在多非线性因素耦合分析中,可以看到在低啮合频率情况下,啮合间隙和啮合刚度对系统非线性特性影响不显著,但当系统进入较高啮合频率,大于 0.1 Hz后,较大的啮合间隙和啮合刚度都会增加系统的线性传动误差.根据上述分析,齿轮应通过材料热处理增加一定齿面硬度,保证系统具有较高的啮合刚度,但不能过硬.齿轮系统不能长时间处于高速状态,系统中的混沌现象严重影响零部件的工作特性和使用寿命.齿轮间隙在满足润滑和散热条件下,应尽量选择较小间隙. (4) 齿轮啮合频率对非线性特性影响最大,啮合间隙其次,啮合刚度影响最小,此结论对齿轮系统生产加工和装配具有一定的理论指导意义.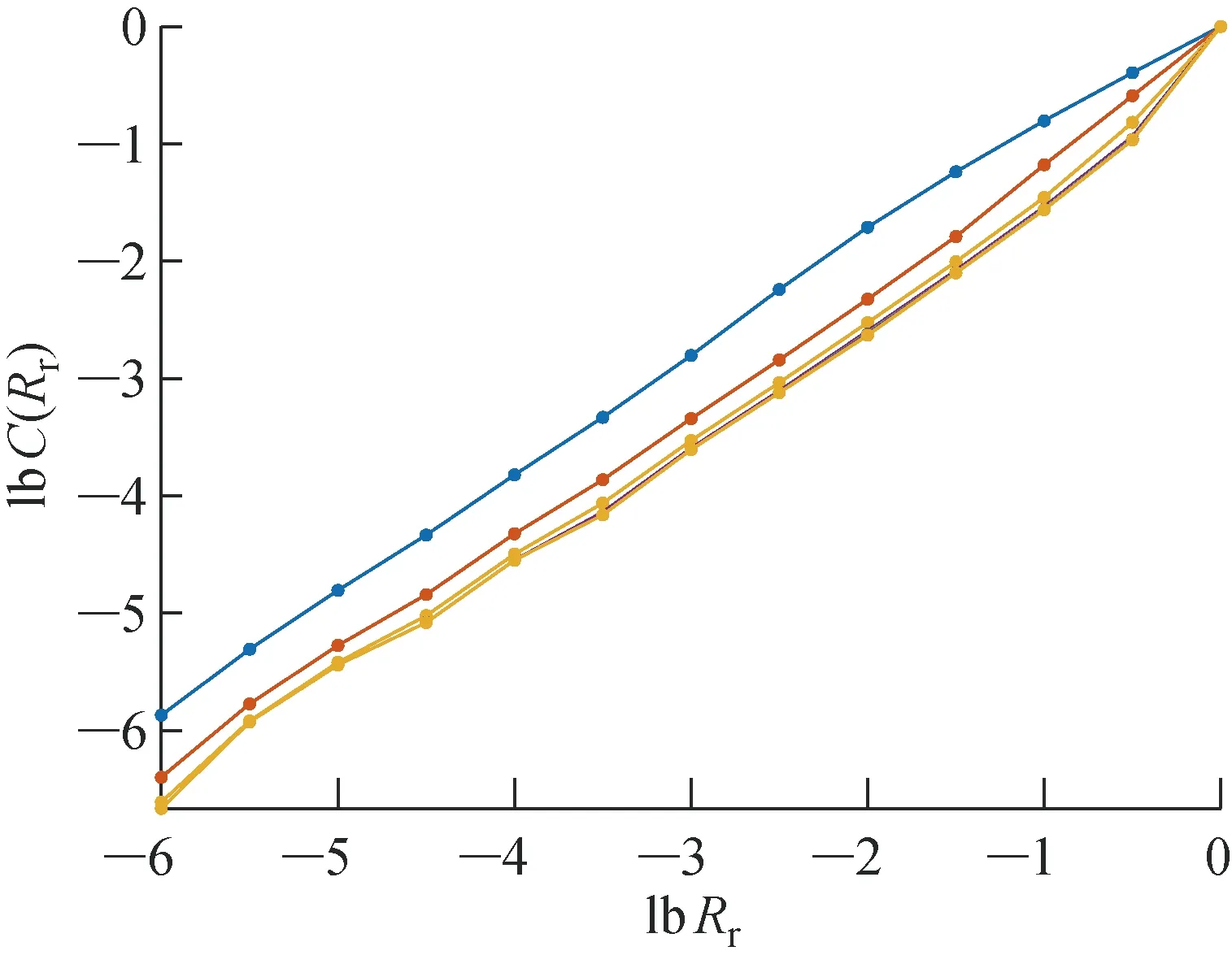
2.4 齿轮啮合刚度对系统动态特性影响

2.5 啮合频率对系统动态特性影响


2.6 啮合间隙对系统动态特性影响




3 非线性因素对系统性能耦合影响
3.1 啮合刚度和啮合间隙对系统动态特性影响


3.2 啮合刚度和啮合频率对系统动态特性影响


3.3 啮合间隙和啮合频率对系统动态特性影响


4 结论

