考虑焊接变形的装配偏差分析在动力集中型动车组中的应用

姚利民， 张道刘， 侯秀娟， 刘 涛， 李志敏

(1. 上海交通大学 上海市复杂薄板结构数字化制造重点实验室， 上海 200240；2. 中车唐山机车车辆有限公司， 河北 唐山 063035)

随着铁路技术的快速发展，不断提升的列车客运速度对与之相配套的轨道交通装备制造业的要求也越来越高.动车组列车作为实现铁路提速的重要核心装备，其车体的装配精度是列车能够满足行驶安全性、乘坐舒适性和运行平稳性设计需求的前提和保障.动车组列车车体具备多级、多层面的产品结构特征，制造工艺流程复杂.为了进一步提升车体的制造精度，除了结合传统的依靠经验和物理样车的车体开发手段之外，还需要通过数字化手段，开展车体关键部件尺寸工程设计和装配偏差模拟等方面的研究工作，实现在产品设计开发阶段对车体装配质量的有效预测，进而提高车体的开发效率和制造精度.焊接作为列车制造过程中零部件连接的主要方式，其焊后不可避免地会产生焊接变形，导致传统的只考虑零件偏差及工装定位偏差的刚性装配偏差分析方法不能准确地预测产品的装配精度[1].因此，考虑焊接变形因素对产品最终装配结果的影响是非常必要的.

焊接因具有能够提高结构性能、增强设计灵活性及减重等优点在大型结构上有着广泛的应用.但是，由于焊接过程中存在局部加热后快速冷却的加工环节，导致在焊缝及其热影响区附近会产生较大的残余应力，从而使构件发生焊接变形.对焊接变形进行准确预测是改善和提高产品装配精度的重要手段[2].热弹塑性有限元法虽然能够有效预测焊接变形和焊后残余应力，但由于其计算工作量大、计算时间长，只适用于中小型结构[3-4].为此，国内外研究人员开展了大量的研究工作以提高计算效率.Peri等[5]研究了壳单元和实体单元混合的数值模拟建模技术，用热弹塑性有限元法计算T型接头的焊后应力和焊接变形，在保证计算精度的同时缩短了计算时间.针对大型结构的焊接变形预测问题，Ueda等[6]将基于固有应变的有限元法成功地应用到变形预测中, 从而将瞬态热弹塑性分析转化为静态弹性力学问题，大大减少了数值模拟的时间.Deng等[7-8]利用固有应变法预测大型船舶结构的焊接变形，研究了初始间隙对最终焊接变形的影响，同时探讨了焊接热输入、焊接工艺、焊接顺序和板厚等因素对屈曲变形趋势的影响.Lee等[9]提出了一种不受焊接区域网格尺寸限制的预测大型结构焊接角变形的方法，基于有限元理论推导出力矩阵的显示形式，并获得了影响焊接角变形的输入变量与网格尺寸的关系，进而依据网格尺寸将焊接变量转化成一个标量作为输入值，较大地提升了有限元的计算效率，最后通过实验验证了该方法预测焊接角变形的有效性.然而，焊接变形并不是影响制造精度的唯一因素.实际上，若想更准确地预测产品的最终尺寸精度，需要同时考虑焊接变形和装配偏差.Lee等[10]模拟了存在定位偏差的情况下，不同焊接工艺参数对最终装配偏差的影响，并通过生成的数据库对装配偏差进行快速查询预测.然而，该方法对于复杂的结构并不适用.Pahkamaa等[11]采用瞬态非线性有限元Monte Carlo法模拟了存在定位偏差时的焊接过程，模拟结果和实验数据的对比表明，焊接变形和定位偏差的影响是不能叠加的.Lorin等[12-13]提出了一种适用于偏差模拟的焊接变形计算(SCV)方法，实现了考虑焊接影响的装配偏差模拟.与传统的瞬态热弹塑性方法相比，该方法的计算时间相对较少.Wärmefjord等[14]通过实验揭示了零件定位偏差对焊后尺寸的影响，同时指出最终的装配能力与零件公差、夹具偏差及由焊接引起的变形密切相关.Renzi 等[15]分别用热弹塑性有限元法和固有应变法研究了零件尺寸公差及在热输入存在波动的情况下铝板的焊接角变形情况，并比较了两种方法在计算精度和计算时间方面的优劣性.

本文以某型号动力集中型动车组的侧墙窗口模块为研究对象，通过固有应变法对大型结构的焊接变形进行数值模拟，并将得到的焊接变形量以均值移动的方式添加到窗口模块的装配偏差分析中.借助三维装配偏差分析软件，预测当同时存在零件偏差、工装定位偏差以及焊接变形的情况下产品的装配精度，并通过与实测数据的对比分析验证该方法的准确性.

1 侧墙窗口模块焊接接头固有应变

1.1 窗口模块的组成

侧墙作为动车组车体组成的关键大部件之一，其装配质量不仅影响着车体外观，同时也影响着列车的运营性能.动车组的侧墙是蒙皮骨架结构，而骨架则是由多个窗口模块通过窗间纵梁焊装连接而成，因此侧墙的制造质量很大程度上依赖于窗口模块的装配精度.窗口模块由折弯乙型梁在工装上组装焊接而成，由于窗口处需要安装玻璃，所以窗口的高度和宽度需要保证一定的精度，其设计值分别为 102.2 和 127.2 cm.装配完成后需要测量窗口的高度和宽度，在实际生产中分别选择3处进行测量，其位置如图1所示.

1.2 固有应变基本原理

固有应变可以看成是内应力的产生源.若将物体处于既无内力也无外力时的状态作为基准态，固有应变就是表征从应力状态切离后处于自由状态时，与基准态相比所产生的应变[16].固有应变ε*由热应变εT、塑性应变εp和相应变εX组成，即

ε*=εT+εp+εX

(1)

在焊接完成热循环并冷却到室温后，其热应变εT为0.对于低碳钢等材料的焊接过程，相应变εX对焊接变形的影响很小，往往予以忽略，此时的固有应变即可用塑性应变εp表示.

针对工程中复杂的大型构件，焊接变形主要包括由焊缝横向应变引起的横向收缩和角变形，以及由纵向应变引起的纵向收缩.若能通过计算测得这两种应变的大小和分布，并施加到焊缝附近，使用线弹性有限元代替热弹塑性有限元求解焊接残余应力和焊接变形，则预测大型工程结构的焊接变形会变得更加快捷.本文使用Sysweld软件对侧墙窗口模块的3种典型焊接接头进行热弹塑性有限元模拟，分别提取横向应变和纵向应变数值，并通过Abaqus软件提供的各向异性热膨胀系数转化功能加载横向应变和纵向应变，进而通过施加温度载荷计算整体模型的焊接变形，其具体步骤如图2所示.

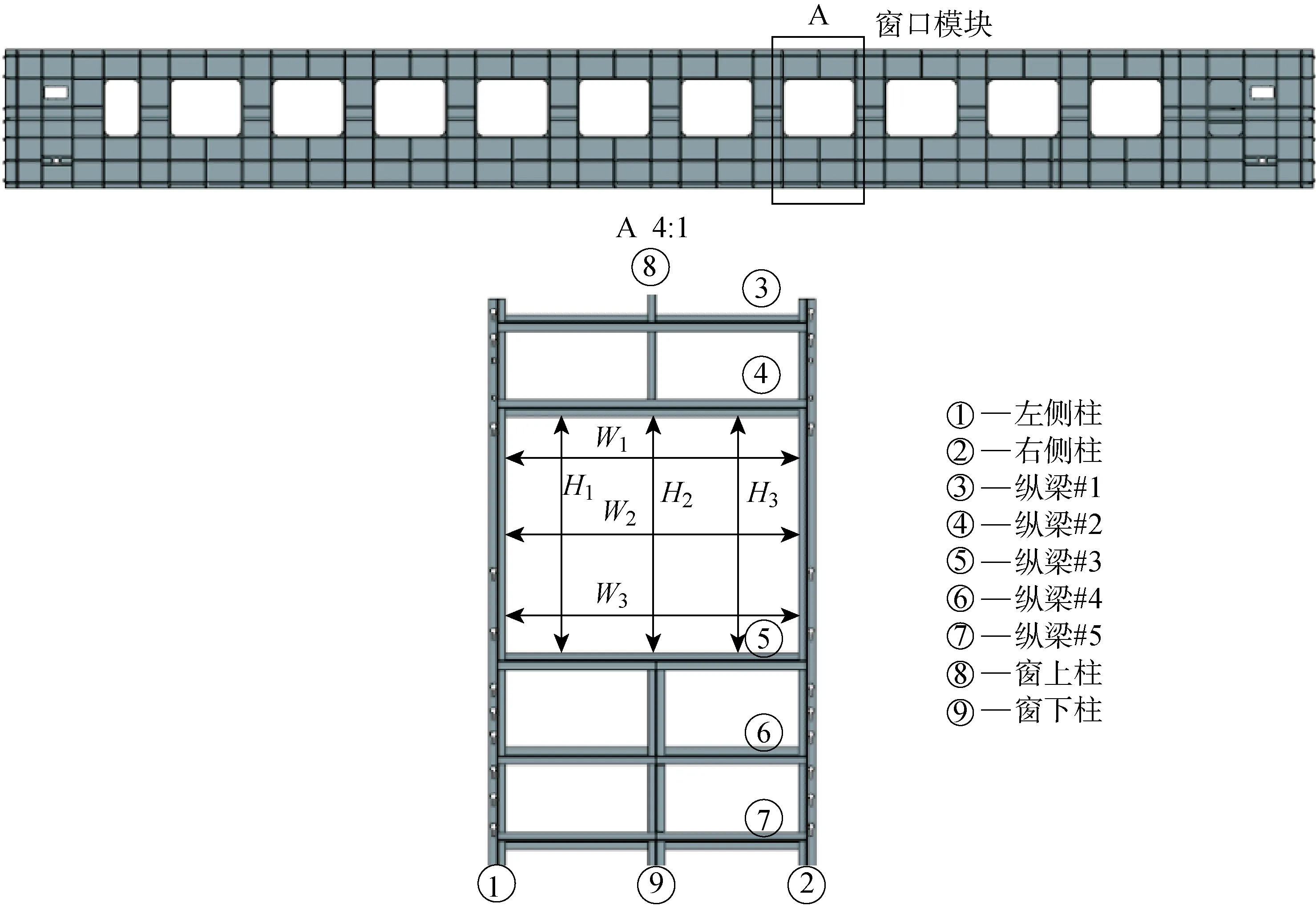
图1 侧墙及窗口模块组成Fig.1 Configuration of the sidewall and the window module

图2 焊接变形模拟路线Fig.2 Strategy of welding deformation simulation

1.3 焊接接头固有应变计算

侧墙窗口模块的焊接工艺规程中共有3种焊接接头，分别对3种接头建立模型，并对其进行网格离散化处理，结果如表1所示.为了得到侧墙窗口模块的整体焊后变形情况，首先需要分析每种焊接接头焊后的固有应变大小及其分布规律.本文采用完全耦合的热弹塑性方法进行数值分析，3种焊接接头对应的焊接工艺参数如表2所示.

表1 窗口模块的3种焊接接头Tab.1 Three welded joints in the window module

表2 3种焊接接头的焊接工艺参数Tab.2 Welding process specification of three welded joints

不同的焊接方法具有不同的热输入特点，建模时应根据需求选择与之相匹配的热输入模型，如Gaussian热源模型、双椭球热源模型等.窗口模块均采用t135-MAG焊接方法，其相应的热输入模型为双椭球热源模型.在Sysweld软件中双椭球热源前半部分(f)和后半部分(r)的热流分布函数分别为[17]

qf(x,y,z)=

(2)

y≥0

qr(x,y,z)=

(3)

y<0

式中：U为焊接电压；I为焊接电流；η为热输入效率；ff和fr为热流密度分布函数，ff+fr=2；a,b1,b2,c为熔池的几何尺寸.

为最大限度地保证工件处于自由状态，并消除结构刚体位移，对3种接头分别施加最小约束条件.完成前处理后，利用Sysweld求解器进行求解并对计算结果进行分析，提取3种接头的固有应变.

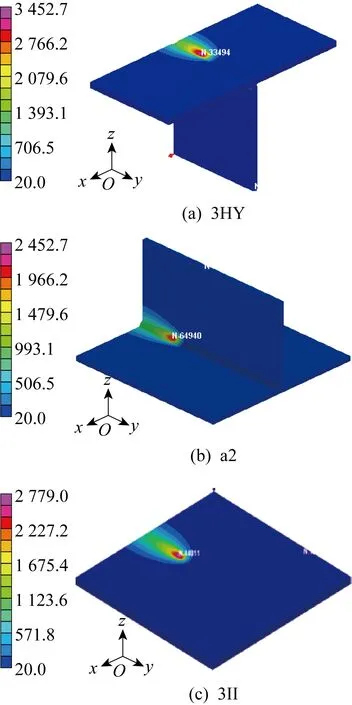
图3 3种接头的瞬时温度场分布情况(℃)Fig.3 Transient temperature distribution of three welded joints (℃)

图3所示为3种接头瞬时温度场的分布情况，从图中可以看出焊缝附近区域的温度均已达到材料的熔点.在焊接起弧阶段，构件上的温度场变化较大，这是由于焊接开始时的热输入比正常焊接时的热输入大，而构件上的温度原本是均匀且相对较低的，当热源引入后热量迅速传递到周围，使得温度场的温度分布不稳定；在焊接收弧阶段，与正常焊接时相比，焊件末端的构件吸收了全部热输入量，因此在焊缝中心的温度较高.在正常焊接过程中，熔池温度随时间的变化很小，这是由于此时焊缝及其附近区域的热量输入和扩散基本保持平衡，整个构件的温度场处于准稳态.

3种接头的焊后等效残余塑性应变分布情况如图4所示.由图可知：残余塑性应变完全集中在焊缝及其附近区域，焊缝附近除了两端以外的大部分区域都处于压缩塑性应变状态；焊缝中间位置的残余塑性应变分布区域较宽，而靠近两端的残余塑性应变分布区域相对较窄，远离焊缝处的应变接近于0.在焊缝中间位置取一个截面，并对焊缝及其热影响区的所有节点的应变求平均值，得到室温状态下焊缝及其热影响区域节点的平均横向(x方向)和纵向(y方向)固有应变大小.但由于在Abaqus软件中，固有应变不能直接作为荷载赋予焊缝及其附近单元，需将其转化为各向异性热膨胀系数才能实现整体模型的变形计算[16]，转化公式为

(4)

(5)

式中：Wx,Wy为x,y方向单位长度上焊缝的总收缩量；A为施加固有应变单元的截面积；αx,αy为热膨胀系数；ΔT为温度变化量.由式(4)和(5)转化得到的热膨胀系数如表3所示.

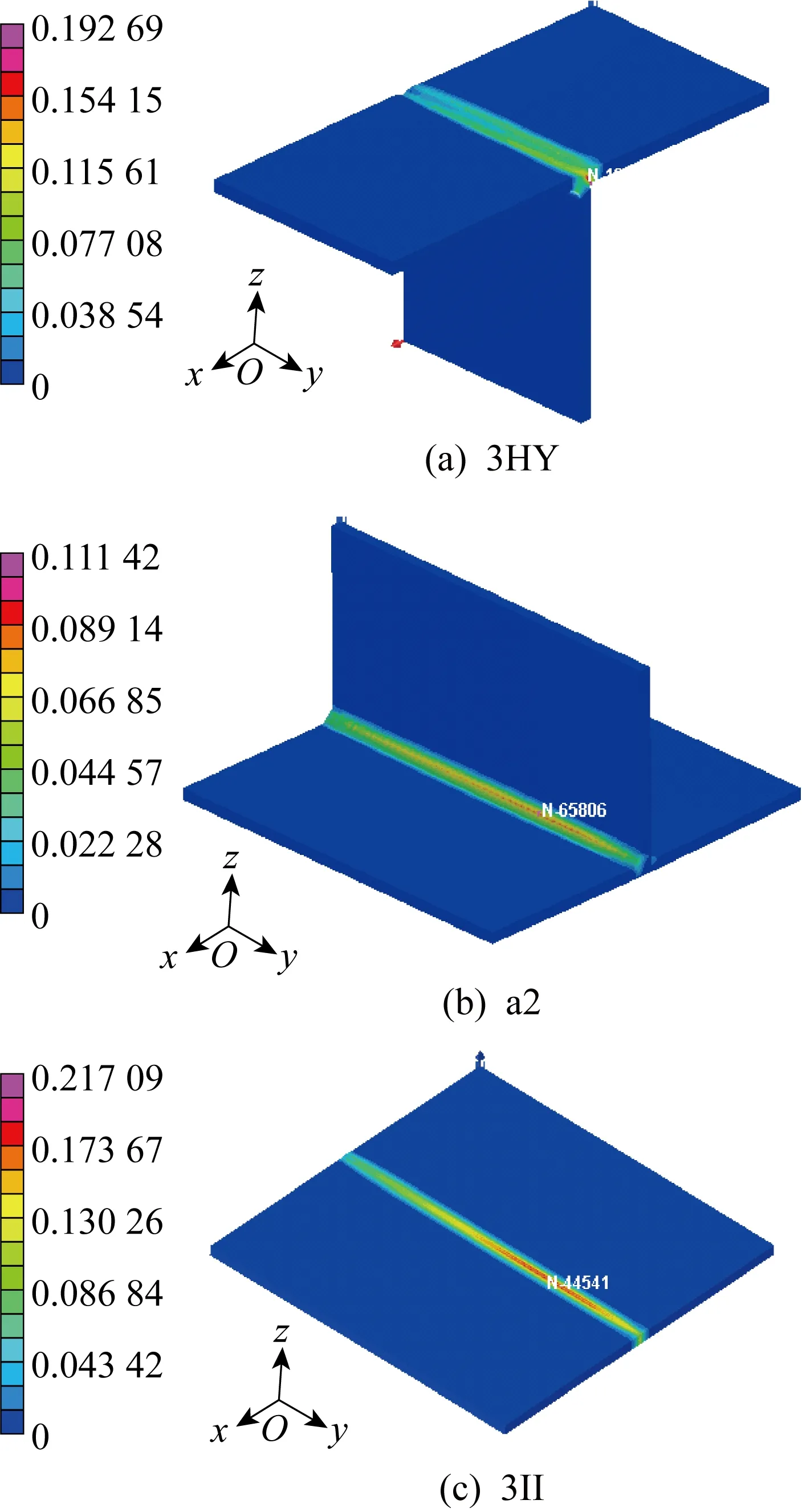
图4 3种接头焊后的等效固有应变Fig.4 Equivalent inherent strain of three welded joints

Tab.3Transverseandlongitudinalinherentstrainofthreeweldedjoints

接头ε∗x/%ε∗y/%αx×105/℃-1αy×107/℃-13HY-4.102-0.084-3.20-6.56a2-5.421-0.140-4.23-10.93II-8.367-0.062-6.54-4.87

2 侧墙窗口模块焊接变形模拟

2.1 有限元模型建立

窗口模块是空间分布着多条焊缝的较大型结构，其整体尺寸为 134.2 cm×243.9 cm(宽×高)，主要由侧柱、纵梁和窗上下小立柱组成.该模块的焊后变形可通过基于固有应变法的有限元模拟进行有效预测.

采用Hypermesh软件对窗口模块的模型进行网格划分，其中绝大部分采用的是C3D8R单元，同时存在极少数的C3D6单元.单元总数为 482 151，节点总数为 731 840，焊缝热影响区域的网格适当加密.

数值分析过程中采用Q345NQR2碳钢材料，其力学性能为:密度ρ=2 700 kg/m3；弹性模量E=210 GPa；泊松比ν=0.33；热膨胀系数α由式(4)和(5)计算得到(见表3).

夹具单元中的定位块与夹紧块大小相当，与工件的定位接触面积较小并且夹紧力足够大，在这种情况下有限元分析将其作为刚性约束处理.窗口模块的整个组焊过程中共有61道焊缝，如图5所示.

根据工艺流程，焊接按照窗口四周焊缝、窗上焊缝以及窗下焊缝的顺序进行，并且由Abaqus软件中的分析步(STEP)实现.将求得的固有应变作为初始应变转换为相应方向上的热膨胀系数，并施加于对应的焊缝附近区域，再通过加载温度载荷进行一次弹性有限元计算，便可以得到窗口模块焊后的整体变形结果，完成预处理的窗口模块模型如图6所示.

图5 窗口模块焊缝图Fig.5 Welding lines of window module

图6 窗口模块焊接过程有限元模型Fig.6 Finite element model of window module

2.2 模拟结果分析

根据焊接结构理论，构件的焊接变形通常用某些特殊点的变形量或沿某一条路径的变形量来衡量.窗口模块焊接完成后的x、z方向位移(Ux,Uz)图如图7所示.

由图7(a)可知，焊后x方向的变形主要集中在侧柱上，最大位移约为 0.98 mm，致使侧柱出现了一定的弯曲，影响了侧柱的焊后直线度；由图7(b)可知，侧柱和窗上下立柱在z方向几乎没有变形，z方向的变形主要集中在纵梁上，最大位移约为 0.78mm，影响了纵梁的焊后直线度.

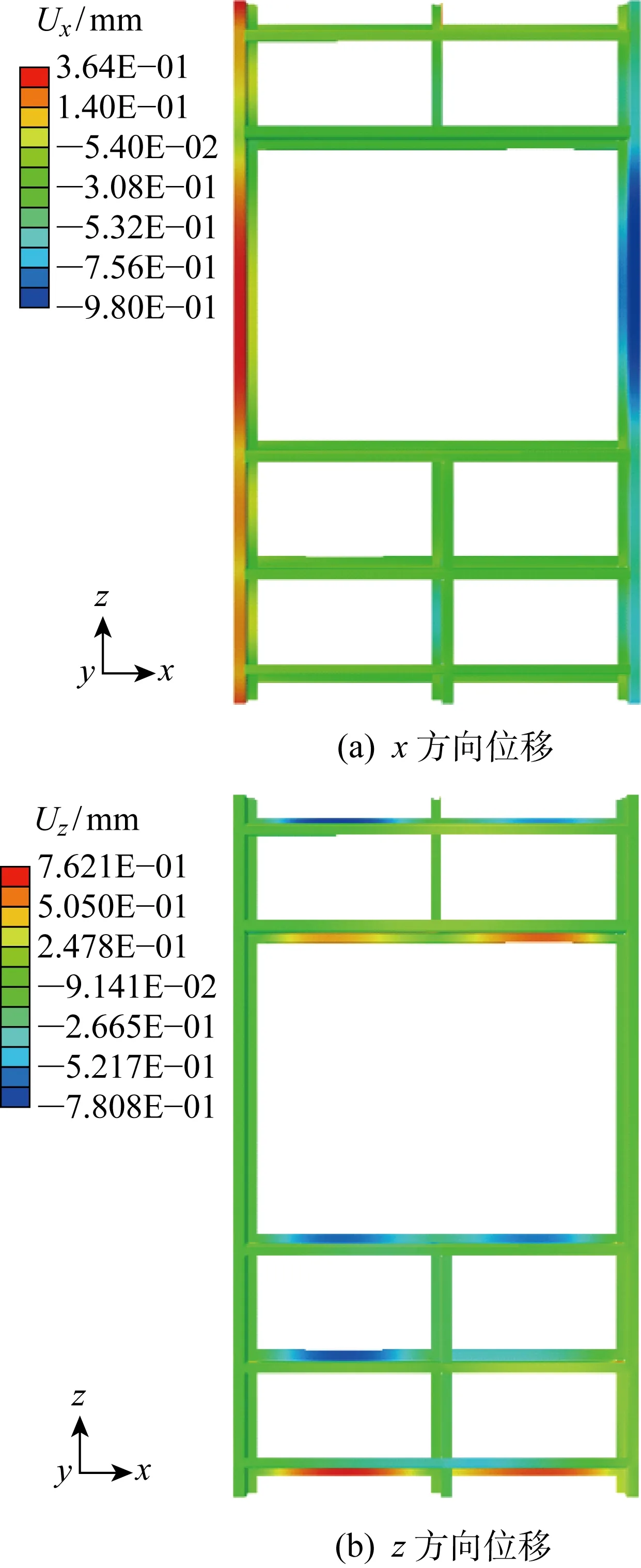
图7 窗口模块焊后变形图Fig.7 Deformation of window module after welding

作为窗口模块的两个关键尺寸，窗口的宽度和高度由于焊接变形的影响，皆出现了不同程度的尺寸变化，图1中对应的3个宽度和3个高度测量点的焊接变形量如表4所示.然而，窗口的最终尺寸并不仅仅和焊接变形有关，还与零件偏差和工装定位偏差有关.因此，若要更准确地预测窗口模块焊接装配后的尺寸， 有必要对窗口模块进行焊接变形装配偏差的模拟分析.

表4 窗口宽度和高度测量点的焊后变形量

3 焊接变形的装配偏差模拟

3.1 窗口模块刚性装配偏差模拟

侧墙窗口模块由9个乙型折弯梁按照一定的装配顺序在工装上组装而成，其装配顺序如图8所示.首先将侧柱摆放到窗口模块工装上，与定位块密贴夹紧；依次将纵梁摆放到工装上，两端与侧柱密贴，然后用夹具压紧；最后将窗上下立柱与纵梁卡紧，完成窗口模块的组装.

对于零件的刚性装配，其装配偏差主要来源于零件的尺寸公差及其在装配过程中的定位偏差.侧墙窗口模块的零件偏差主要有侧柱和纵梁长、宽、高度的尺寸公差，侧柱和纵梁的直线度、垂直度、平面度等形位公差，而定位偏差则主要来自工装的平面度误差.窗口模块的零件公差如表5所示.

图8 窗口模块装配顺序
Fig.8 Assembly sequence of window module

表5 窗口模块的零件公差Tab.5 Tolerances of parts of window module

刚性装配偏差模拟在3DCS软件中进行，将零件按照图8所示的顺序进行虚拟装配，分别输入表5中的公差信息，并设定如图1所示的窗口高度和宽度测量点的测量值，然后运行1 000遍Monte Carlo模拟，分别得到窗口高度和宽度的刚性装配偏差模拟结果.

3.2 模拟结果和实测数据对比

为了更准确地预测窗口模块的装配结果，需要在刚性装配偏差的基础上考虑焊接变形量的影响.由于计算所得的焊接变形量是一个定值，而刚性装配偏差模拟的结果是一个统计值，所以本文将焊接变形量以均值移动的形式叠加到刚性装配偏差模拟结果的均值上，标准差保持不变，从而实现考虑焊接变形的窗口模块装配精度分析.按照图1所示的测量位置，在实际操作中测量了40组窗口模块的宽度和高度，通过计算得到窗口宽度和高度的均值和标准差.模拟结果和实际测量结果如表6所示.

为了更直观地比较模拟结果和实测数据的吻合程度，这里假设模拟结果和实测数据均服从正态分布，以实测数据的±3σ为置信区间作为模拟结果的上下限(LSL, USL)，在置信区间内的模拟结果认为是准确可信的，反之，则认为是不准确的.验证结果如图9所示.从图9可以看出，窗口宽度和高度的模拟结果基本都位于实测结果的置信区间内.其中：窗口宽度W1、W2和窗口高度H1、H2的模拟结果和实测数据的吻合度很高；W3和H3的模拟结果和实测数据的吻合度相对较低.考虑到实际装配过程的复杂性，本文提出的模拟方法可以较为准确地预测窗口模块关键尺寸的装配精度，同时也表明该方法对焊装结构的装配精度预测是有效且可行的.

表6 模拟结果和实测结果对比(mm)Tab.6 Comparison between simulation results and actual measurements (mm)

图9 模拟结果准确性验证Fig.9 Accuracy verification of simulation results

4 结语

本文以动车组侧墙的窗口模块为研究对象，利用基于固有应变的有限元方法计算窗口模块的焊接变形，提出将焊接变形量以均值移动的方式添加到窗口模块的装配偏差分析中，并通过对比窗口宽度和高度的实测数据与模拟结果，验证了该方法对预测焊装结构装配精度的准确性和可行性.因此，窗口模块的装配精度模拟结果可作为预测窗口关键尺寸的依据，并可为制定合适的工艺规程提供参考，从而提高产品的一次合格率和制造质量.