基于正六边形网格划分的改进非均匀分簇算法
卢 龙,宋仁旺,康 琳
(太原科技大学 电子信息工程学院,太原 030024)
无线传感器网络是一种面向应用的网络,被广泛应用于军事监控、农业和医疗健康的监测与监护等领域[1]。其节点布置密集和数据采集的周期性,易形成大量冗余数据,极大地消耗了节点有限的能量。目前,常用的节能方法是路由节点在数据转发之前进行数据融合处理[2],使有效数据得到最大程度压缩,从而降低冗余。
LEACH是经典的分簇路由算法代表之一[3],与传统的静态路由比较,更适合现阶段大规模、实时性要求高的网络,可以有效延长网络生存周期,但LEACH协议存在的缺陷是簇头选举时未能考虑节点的剩余能量和节点能耗均衡,单跳通信易造成“热区”等[4]。EEUC[5](Energy Efficient Uneven Clustering)作为一种有效的非均匀分簇路由算法,解决了LEACH协议带来的“热区”问题,即,通过簇间多跳模式进行数据传输,利用节点竞争半径使得离基站越远的簇的范围越大,从而节约簇内能量用于簇间使用。文献[6]主要通过网络分区,使得距离基站远近不同的分区内簇个数不同来均衡簇间与簇内能耗。特别地,文献[7]采用权值局部竞选簇头,簇头通过距离数值等构建半径不等的多个簇。文献[8]采用动态成簇和休眠/唤醒机制来改进非均匀分簇算法。文献[9]考虑成员节点到簇头的距离、节点密度、剩余能量等因素来优化簇头选举。
以上非均匀成簇算法采用不同方法对网络簇头选举、竞争半径以及路由通信设计来实现网络节能,但EEUC算法仍然存在的缺陷是网络内仍存在大量的数据冗余、簇头选举频繁能耗较多等。本文提出的基于正六边形网格划分的改进非均匀分簇算法(Uneven Clustering Algorithm Based on Hexagonal Grid,HGUC)在网络正六边形虚拟网格划分的基础上,选举每个网格内能量最大的节点作为备选簇头,休眠冗余节点,从根本上减少重复数据的采集,减少簇头轮换次数,有效延长网络生存周期。
1 网络模型
1.1 节点模型
将N个传感器节点随机布撒于L×L区域内,固定sink节点。传感器节点通过感知簇头请求信息强度大小选择最近簇头发送数据,簇头融合数据后发送至sink节点。其他基本假设如下:①所有布撒的节点静止且能量有限;②节点有独立的ID号,sink节点位置已知;③节点通过RSSI值得到其与sink节点的距离;④传感器节点和sink节点自身传输半径可以任意改变。
1.2 能耗模型
ETR(L,D)=Etr-elec(l,d)+Etr-comp(l,d)=
(1)
ERX(l,d)=l·Eelec
(2)
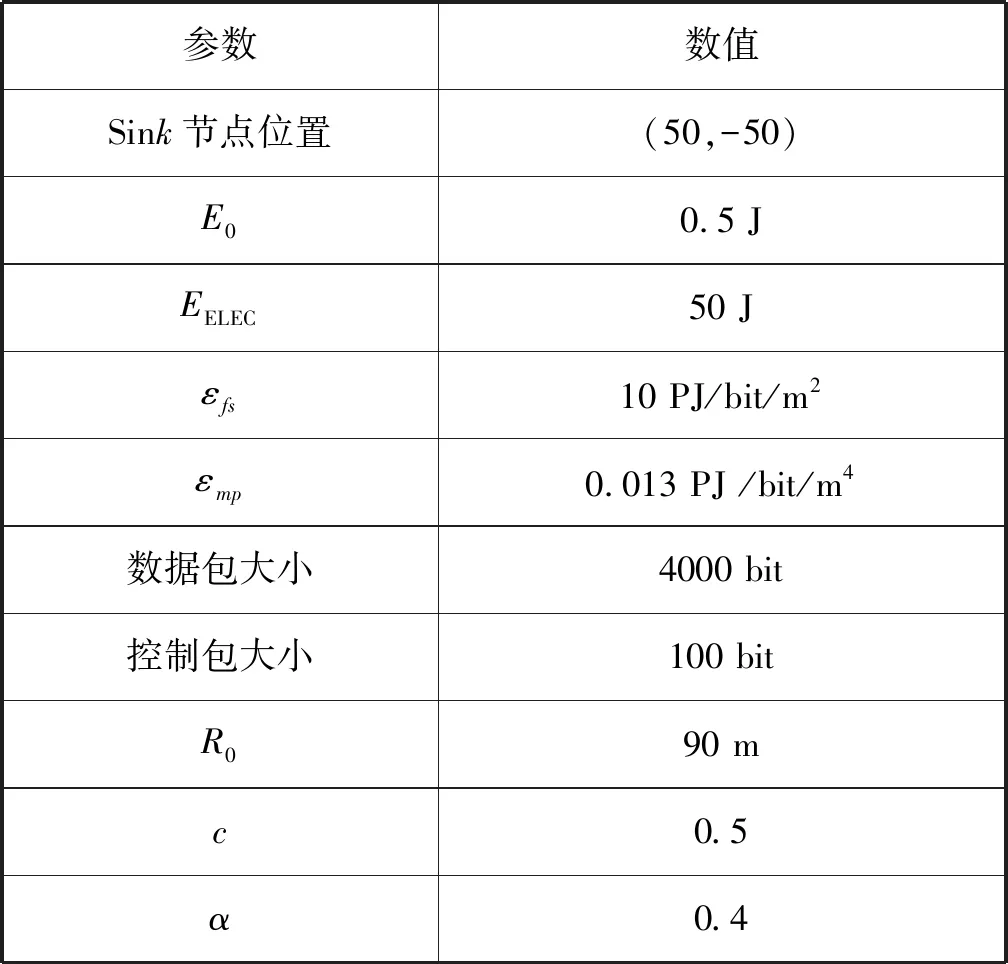
其中,ETX,ETR分别为发射节点和接收节点能耗,Eelec为传输1bit数据能耗,l表示传输数据包的长度,εfs,εmp分别表示在自由空间模型和多径衰减模型下功率放大器的能耗系数,当d (3) 针对上述EEUC协议的问题,提出改进HGUC算法,算法同样采用EEUC协议“轮”的工作过程。在成簇阶段,首先对网络监测区域进行虚拟正六边形网格划分,选举每个网格当前能量最大的节点为备选簇头,使网格内剩余节点处于休眠状态,以降低数据冗余;其次,根据备选簇头与基站距离和簇头当前网格节点密度、节点剩余能量等,确定最终簇头,并使网络每1/p轮进行一次簇头选举,从而减少频繁簇头选举次数和改进簇头竞争半径来构造大小不等的簇;在稳定数据传输阶段,簇间采用多跳的数据传输模式,有效的延长网络生存周期。 2.1.1 正六边形网格划分理论分析 在无线传感器网络中,传感器节点以辐射圆覆盖,对于有限的节点传感半径,通过几何推导图1所示:当三圆两两相交,圆心构成的三角形为等边三角形时,三圆所覆盖的有效面积最大,且圆之间重叠部分面积最小[11-12],可以用最少的节点个数,实现目标区域的全覆盖,同时最大程度的减少数据冗余。按照上面的理论,对传感器网络进行节点覆盖,如图2所示。 其三,依照建构主义的思路,我们可将中国与中南半岛国家间的文化外交理解为国家间通过互动交往形成共同知识的过程。虽然建构主义并不认为文化必然意味着合作,但在解释施动者与结构的关系方面却具有自我循环的色彩。如温特认为:“施动者通过从事某些实践活动造就和再造了社会结构,社会结构又建构并规范这些实践活动以及与之有关的身份。”而关于施动者(如国家)起初为何会以特定的文化方式开展实践行为,温特则假定施动者“带着关于自我身份的预设观念开始第一次相遇,这种预设观念使他们具有暂时的角色,并成为他们互动的起点”。 [10]但上述假设并没有解释“预设观念”的形成原理,这也正是本研究需面对的问题。 图1 三圆两两相交 图2 用最少的节点覆盖监测 在保证节点圆形覆盖的情况下,将两两圆重叠的区域进行简化,如图3所示,用直线段代替圆的重叠区域,即得到圆的内接正六边形,这种内接正六边形几乎圆形的理想节点覆盖模型,无缝也无重叠,尤其适用于区域设计与网络划分。按以上方法将目标网络正六边形划分,一旦已知节点的传感半径,就能用最少节点数量实现区域全覆盖。与正方形划分方法比较使用的节点更少,且网络规模越大、多跳传输距离越长,无线传感器网络节能效果越好。 图3 简化网格分布 图4 监测半径和边长的关系 2.1.2 网格边长及节点位置的确定 如图4所示,目标区域被划分为多个正六边形,任意两个相邻的网格内节点最大监测距离大小与节点监测半径d和正六边形边长r关系如下可得: (4) 图5 网络划分 图6 网格编号 (2)确定网格的编号 如图(6)所示,作长为2m宽为2n的矩形,其中,正六边形边长设为L,m和n分别为单位坐标长度,各个网格的中心点(x0,y0)所属的网格编号为 (3)确定每个节点(xi,yi)所属网格编号C_ID(i),流程如表1: 表1 网络节点编号 网络节点编号(归格)n=sqrt(3)∗L/2 //单位x轴y轴长度 m=3∗L/2 k(i)=floor(X(i)/n) //网格编号z(i)=floor(Y(i)/m)a(i)=X(i)-k(i)∗n b(i)=Y(i)-z(i)∗mif(mod(( k(i)+z(i)),2)=0) //网格横纵坐标之和为偶数if(a(i)2+b(i)2)<=(n-a(i))2+(m-b(i))2if(mod(k(i),2)==0&&mod(z(i),2)==0)//横、纵坐标都为偶数C_ID(i)=4∗k(i)+z(i)+1else C_ID(i)=4∗(k(i)-1)+z(i)+1endelseif (mod(k(i),2)==0&&mod(z(i),2)==0) //横、纵坐标都为偶数C_ID(i)=4∗k(i)+z(i)+2elseC_ID(i)=4∗(k(i)+1)+z(i)+2endendelse //网格横纵坐标之和为奇数if(mod(k(i),2)==0&&mod(z(i),2)~=0) //横坐标为偶、纵坐标为奇if (a(i)2+(m-b(i))2<=((n-a(i))2+b(i)2))C_ID(i)=4∗k(i)+z(i)+2;elseC_ID(i)=4∗k(i)+z(i)+1;endelse //横坐标为奇、纵坐标为偶if (a(i)2+(m-b(i))2<=((n-a(i))2+b(i)2))C_ID(i)=4∗(k(i)-1)+z(i)+2;elseC_ID(i)=4∗(k(i)+1)+z(i)+1;endendend 2.2.1 簇头选举 HGUC算法是非均匀分簇算法的改进,算法先将网络正六边形网格划分,遍历每个网格选出能量最大的节点作为备选簇头节点,避免了通过给定阈值选出的备选簇头能量不足的缺陷,同时考虑到每个备选簇头网格内存活节点数,确保网格具有存活节点、节点较密集且能量较大的备选节点成为最终簇头节点,具体算法描述如下: 1)分簇阶段,首先确定网络最优簇头节点个数:簇头节点个数的多少在一定程度上影响着网络的能耗,本文采用文献[6]中最优簇头数算法,现将最优簇头数表示如式(5): (5) 从式(5)可知,最优簇头个数与网络节点个数n、网络区域边长A、sink节点与网络区域中点距离LBS有关。 T(n)= (6) 3)设定成簇半径,根据文献[8]选出的簇头和簇头到基站的距离,计算簇头的竞争半径Rc,考虑到距离基站较远的簇头竞争半径越大用于簇内数据传输能耗也大,因此在计算竞争半径考虑到节点剩余能量,竞争半径修改如式(7): (7) 式(7)中:dmax和dmin分别表示网络中簇头节点到基站的最大和最小距离,R0为所有节点在网络初始化时的半径,E0,Er(i)分别表示节点的初始能量和第r轮簇头节点i的当前能量,表示节点i与sink节点的距离,c被定义为半径控制因子,其取值范围为c∈(0 ,1). 本文的实验结果是在MATLAB仿真平台上实现的,在目标监测区域为100 m×100 m,随机部署400个传感器节点,实验网络模型的相应参数设置如表2: 表2 仿真参数Tab.2Simulationparameters 参数数值Sink节点位置(50,-50)E00.5 J EELEC50 Jεfs10 PJ/bit/m2εmp0.013 PJ /bit/m4数据包大小4000 bit控制包大小100 bitR090 mc0.5α0.4 本部分通过仿真实现正六边形边长对网络性能的影响,同时比较了HGUC算法与LEACH算法、EEUC算法在执行了2500轮时网络生存周期、平均节点剩余能量的变化。 400个传感器节点随机部署于100 m×100 m的监测区域,节点位置及覆盖图如图7所示。 图7n=400时,网络覆盖 如图“·”代表传感器节点,在节点传感半径r=10 m情况下,监测区域被400个节点重复监测,造成大量的数据冗余,极大的消耗了节点有限能量。当区域通过正六边形网格划分后,找出每个网格能量最大的节点作为备选簇头节点,休眠其他节点,在同样的传感半径情况下,网络被分成52个网格时节点分布覆盖如图8: 图8n=52时,网络覆盖 由图8可知,采用网格划分方式从根本上减少了冗余数据的采集,很大程度上节约了采集重复数据能耗,同时从图中可以看出正六边形划分网络实现98%以上覆盖,在保证网络绝大多数覆盖的情况下,使得网络用于传输有效数据的能耗达到最小。 图9 正六边形边长对网络生存周期的影响 将全部节点死亡定义为网络生存时间的结束,图10、图11分别比较了LEACH、EEUC、HGUC算法执行2500轮后,网络死亡节点数和节点的平均剩余能量。LEACH算法、EEUC算法的首个死亡节点各自出现在587轮、886轮,当分别执行到830轮、1030轮时节点全部死亡,网络不在连通。本文采用HGUC算法,由于每1/p轮进行簇头轮换选举,同时考虑节点的剩余能量和节点密度等因素,极大的减少了冗余数据,节点的平均能耗得到了很好的均衡,首个死亡节点出现的轮数较晚为992轮,2322轮时节点全部死亡,生存周期比LEACH算法提高了58.84%、比EEUC算法提高了51.68%. 图10 死亡节点数比较 图11 节点平均剩余能量比较 本文针对EEUC算法簇头选举频繁耗能较多、没有考虑剩余能量、网络仍存在大量的数据冗余的缺点,提出更节能高效的HGUC算法,算法首先将网络正六边形网格划分,备选簇头和最终簇头选举考虑能量、网格节点密度、最优簇头个数,簇半径大小的设定根据簇头与基站的距离、节点剩余能量等因素,从而极大的减少冗余数据采集和网络能耗。仿真实验表明:HGUC算法与LEACH算法、EEUC算法比较,网络生存周期均得到显著提升。2 算法设计与实现
2.1 协议的理论分析及网格划分

Fig./span>.1ThreeCirclesIntersection
Fig./span>.2TheleastnodestocovertheMonitoringArea
Fig..3Simplifiedgriddistribution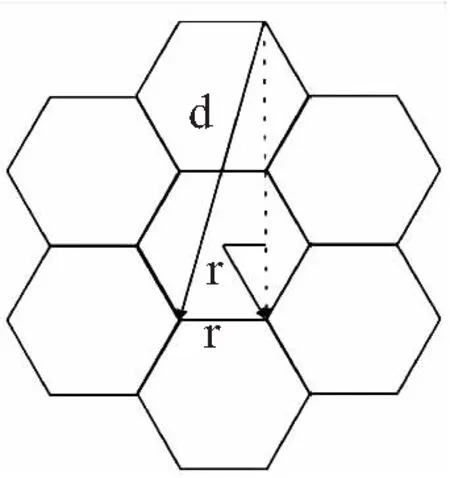
Fig..4Therelationshipbetweenradiusandlength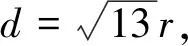
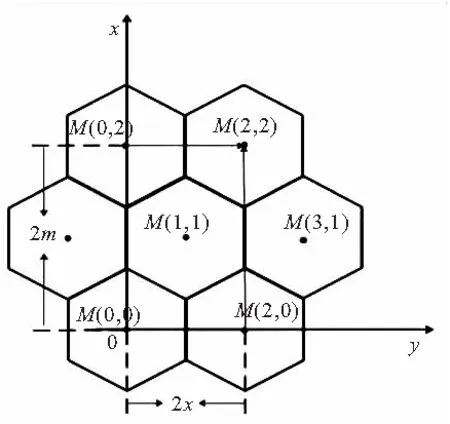
Fig.5 Network partitioning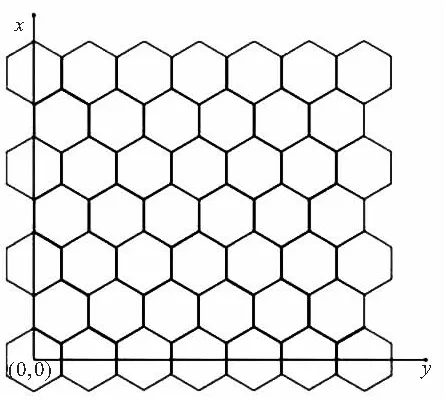
Fig.6 Network number
Tab.1 Grid number
2.2 HGUC算法

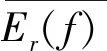
3 仿真与分析
3.1 仿真参数设置
3.2 仿真结果与分析

Fig.7 Network coverage whenn=400
Fig.8 Network coverage whenn=52

Fig.9 The influence of hexagonal lengthon the network lifetime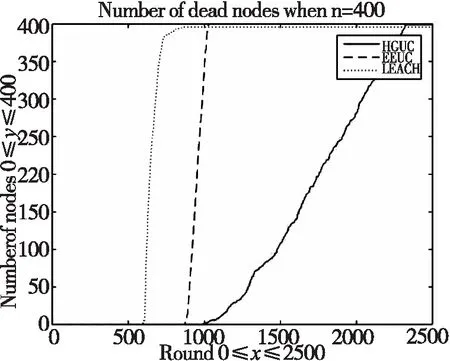
Fig.10 Comparison of death nodes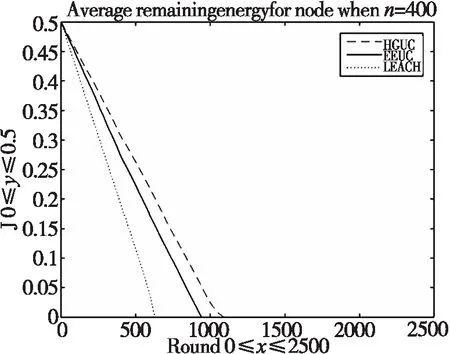
Fig.11 Comparison of average residual energy of nodes4 总 结

