基于粒子群与神经网络的光伏逆变器设计
张玉 周睿 张烈平
关键词: 粒子群优化; 神经网络; 光伏逆变器; 算法; 逆模型; 谐波含量
中图分类号: TN711?34; TM615 文献标识码: A 文章编号: 1004?373X(2019)02?0085?04
Design of photovoltaic inverter based on particle swarm optimization and neural network
ZHANG Yu1,2, ZHOU Rui1, ZHANG Lieping1,2
(1. School of Mechanical and Control Engineering, Guilin University of Technology, Guilin 541004, China;
2. Guangxi Key Laboratory of Building New Energy and Energy Saving, Guilin University of Technology, Guilin 541004, China)
Abstract: The PI control has the advantages of simple structure, good robustness and high reliability, but its parameter setting is difficult, and it is unable to track the system changes well in the complex nonlinear condition of the photovoltaic power generation system. In allusion to the above problems, an inverter model is established and analyzed, and on this basis, an inverter control algorithm based on the combination of particle swarm optimization and neural network is proposed. The off?line optimization is conducted for the system, taking the absolute error and the total harmonic aberration rate as constraint conditions, so as to obtain the samples of optimal PI parameters. The samples are trained by using the neural network to obtain the inverse model of the system. The changing load is compensated to make the output better follow the system changes. The results of system simulation and experiment show that the method can effectively improve the dynamic response speed of the photovoltaic inverter and reduce the harmonic content of the output voltage.
Keywords: particle swarm optimization; neural network; photovoltaic inverter; algorithm; inverse model; harmonic content
正弦波交流逆变电源是光伏并网、交流调速等电力电子设备的核心装置,其对逆变器的交流侧输出波形都有较高要求[1]。如并网时,要求逆变器输出波形总畸变率(Total Harmonic Distortion,THD)限值5%,功率因数不小于0.95(超前或滞后),这需要逆变器具有较强的抗扰能力以及较快的动态响应[2]。为得到高质量的输出电压和较好的功率因数,光伏发电系统逆变器一般采用电压外环和电流内环的双闭环控制策略,决定双闭环控制效果的关键是其PI参数的确定。双闭环控制系统设计的难点是在确定外环与内环参数时,需要综合考虑它们相互之间的影响[3]。
传统的双闭环控制方法为达到较好的效果,需建立精确的系统模型,通过凑试法等确定较为合适的PI参数[4]。但由于光伏发电系统经常会发生负载变化或直流侧电压突变,系统矩阵、闭环特征值及动态响应均会发生改变,造成参数难以适合变化后的系统。尤其针对光伏发电系统的非线性特性,其建模过程复杂,参数凑试困难,难以实现参数的实时调整[5]。针对上述问题,提出了一种基于粒子群与神经网络相结合的逆变器控制算法。PSO算法只需选择一个合适的评价函数,即可找到当前系统状态下的最优参数值,算法简单。由于双闭环PI控制策略一旦设定好参数,在系统运行时就很难根据变化的系统进行实时更改,无法快速跟随系统[6]。所以将变化的负载视为扰动项,利用神经网络拟合,建立系统逆模型,进而可以在控制器处进行补偿,用以抵消负载变化引起的扰动,从而使输出能较快地跟随系统变化。
1 逆变器主电路模型
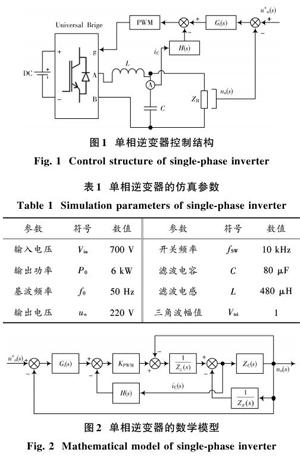
逆变器主电路如图1所示,模型参数如表1所示。系统采用双闭环控制策略,外环为基于PI控制设计的电压环,[Gi(s)]为控制器,内环为系数是H的电容电流反馈,对于电压型逆变器而言,其首要目标是控制输出电压[uo(s)],使其符合理想输出波形。其中KPWM为脉宽调制比例系数,[ZR]为负载的阻抗,L,C为滤波电感与滤波电容,它们构成滤波器,由图1可以得到单相逆变器的数学模型,如图2所示。
对图2进行等效变换,并进行化简,可以得到传递函数:
[Gs=uo(s)u*o(s)=Gi(s)KPWMCsC2Ls3+LZRs+HsCKPWM+GisKPWMCs+1] (1)
式中,系统会因负载阻抗[ZR]的变化而变化,若要使系统达到较好的控制效果,需要根据阻抗来调整控制器[Gi(s)]。使用PI控制器,一旦PI参数确定,便无法修改,而实际应用中,负载经常会因电力设备的接入或断开而发生变化,传统的PI控制器不能根据负载变化而做出相应调整,故控制效果不算理想。
2 粒子群与神经网络控制器的设计
通过对上述模型分析,可知,能否得到高质量的电压输出,关键是PI参数的整定,和对负载变化的控制。针对PI参数选取的问题,采用PSO寻优算法,对PI值进行离线优化;对于由负载变化引起的非线性问题,通过对不同负载情况下系统的仿真,得到大量系统状态的样本,然后利用BP神经网络进行学习,得到控制器到负载处的系统逆模型,并利用它对控制器处进行补偿,以此抵消负载变化的影响,从而达到较好的控制效果。
2.1 基于粒子群算法PI参数调整
粒子群算法又称为PSO算法,是一种典型的群智能算法。大量试验表明,PSO的优化能力强于GA等进化算法[7]。粒子群由一定数量的个体组成,个体可以在指定的空间中根据自身历史最优位置信息和整体最优位置信息,调整位置与移动速度,向更优区域靠拢[8]。
粒子群的更新方式为:
[vijt+1=wvijt+c1r1xPijt-xijt+ c2r2xGgjt-xijt] (2)
式中,w为惯性权重,用于平衡局部优化和全局优化能力。通過大量实验,Shi和Eberhart指出在[0.9,1.2]内粒子群很容易搜索到全局最优区域。在此前提下,w小于0.8时能快速寻优[9];i和j分别代表第i个粒子的数量和第j维(维数代表参数数量);t代表迭代次数;xij则为粒子个体;vij为粒子更新速度;c1和c2为加速因子;r1和r2为0~1之间的随机数;[xPij]为个体最优粒子;[xGgj]为全局最优粒子。
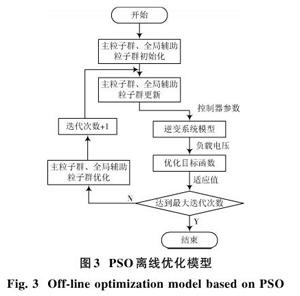
粒子群离线优化控制器参数的模型如图3所示,PSO在每个迭代周期中,将当前粒子代表的控制器参数输出至逆变模型的控制器;然后得到逆变模型的输出电压值,通过计算,得到目标函数的适应值,再将其输入回PSO中,进行优化。目标函数是PSO在当前区域寻优过程中的评价标准,目标函数值越小,代表寻优区域越优。因此通常将系统性能指标设为目标函数[10]。对于本系统,最关键的性能指标就是负载电压误差,但负载电压中含有多次谐波,为保证误差与总谐波畸变率尽可能小,将误差的绝对值积分和总谐波畸变率作为优化目标函数,该公式为:
[F=a0te(t)dt+b·THD] (3)
[THD=n=2∞U2zonUzo1×100%] (4)
式中:[Uzo1]和[Uzon]分别为负载输出电压基波幅值和各次谐波幅值;THD反映了各次谐波所占比重之和的百分比,体现了交流输出电压谐波的含量;[a],[b]为常系数,用来保证负载反馈电压能很好地跟踪指令电压,同时还能保证该反馈电压波形的谐波含量较少。根据表1逆变器仿真参数和图3 PSO离线优化模型,将[KP]的优化区间设为[0.01,5],[KI]的优化区间设为[1,10 000],电容电流反馈系数H的优化区间设为[0,2],通过参考部分文献,并多次实验分析,将PSO相关参数[a],[b],[c1],[c2]和[w]分别设为0.1,0.9,1.45,1.45和0.9,经过大约20 min的优化,得到[KP],[KI],[H]的参数分别为0.24,979和0.013。
2.2 基于BP神经网络的逆模型补偿控制器设计
BP学习算法实质是求取网络总误差函数的最小值问题,具体采用“最速下降法”,按误差函数的负梯度方向进行权系数修正[11]。若将负载电流[iR]看作扰动量,则在相应位置加入同幅值的补偿,即可抵消负载变化的影响,由于实际系统无法在负载处补偿,因此将补偿点前移,得到前馈控制图,如图4所示。
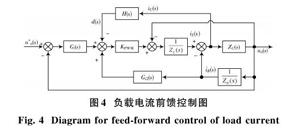
图中:[d]为逆变桥的调制信号;[iL]为电感电流,设两者之间的关系为[iL=f(d)],则[Gi2s=df-1(iL)];由于实际控制中采用离散变量,所以设逆变器的第k个控制周期为k,并依据对逆变器输出电压影响因素的分析,在该周期对参考电压[u*o]、输出电压[uo]、电感电流[iL]、逆变器PWM控制信号采样,分别记为[u*ok],[uo(k)],[iL(k)],d(k)。为了更好地反映出系统的动态特性,将其前一周期的采样值[u*ok-1],[iR(k-1)],[iL(k-1)],[d(k-1)],[uo(k-1)]也作为输入,当前周期的PWM控制信号d(k)作为输出,构建一个包含9个输入和1个输出的动态BP网络。选取隐含层神经元个数为15。
为获得神经网络逆模型的训练样本,对所建立的参数如表1所示的逆变器仿真模型进行仿真实验,对逆变器运行数据进行记录。其中,对于负载,共选取6种不同线性和非线性负载,以[2 μs]為采样周期进行一个周波即0.02 s的样本采集,所有情况一共得到60 000个样本。均匀抽取其中的58 000个样本作为逆模型训练样本,剩余2 000个样本作为逆模型精度检验样本。
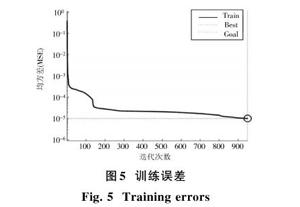
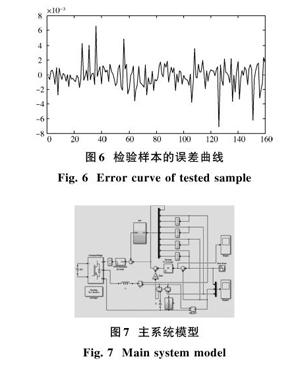
对上述样本进行训练后,得到神经网络模型,其训练误差如图5所示,训练算法可迭代次数949次时便快速达到全局最优,计算在检验样本上的均方差MSE,得出MSE=10-5,说明模型具有较高的精度。部分检验样本的误差曲线如图6所示。
3 仿真验证
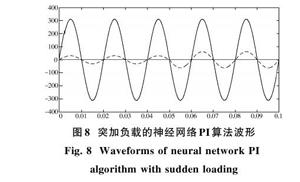
为了验证上述控制方法下系统运行效果,在Simulink中构建了单相光伏并网系统,具体逆变器主要参数见表1,采样时间Ts为[2×10-6 s],仿真时长为0.1 s,[KP],[KI],[H]的参数分别为0.24,979和0.013;在t=0.05 s时,突然加入感性负载。仿真模型如图7所示。该仿真模型与同样参数的传统双闭环PI逆变器模型进行比较。
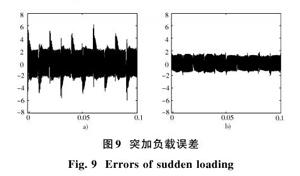
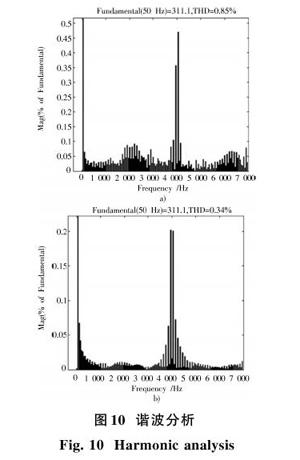
使用训练好的神经网络控制器对逆变系统进行控制,仿真后的电压、电流波形见图8,误差波形如图9b)所示,谐波分析如图10b)所示。
同样条件下,传统双闭环PI控制误差波形如图9a)所示,谐波分析如图10a)所示。
由图8和图9可知,在带固定电阻性负载情况的0~0.05 s时间段,常规PI控制方法的逆变器输出电压波形和电流波形与基于PSO和神经网络的PI自整定逆变器均可以较好地跟随参考电压的幅值、相位,并且保证了电流与电压的频率、相位一致。从图9可以看出,在T=0.05 s时突然加入负载后,逆变器输出受到一定影响,发生了细微波动,但迅速回到稳态。将图9a)和图9b)进行比较可以明显看出,基于PSO和神经网络的PI控制与传统双闭环PI控制相比,前者稳态误差在±1.5 V内波动,在突加负载时,产生的扰动明显较小;同样PI参数的后者稳态误差在±4 V内波动,且在突加负载后,产生了高达6 V的波动。通过图10a)和图10b)的比较可以看出,前者的谐波含量小于后者。
4 结 论
本文提出基于PSO优化PI控制器参数并使用BP神经网络建立逆模型进行补偿的光伏并网逆变器设计方法,可自动寻找PI控制器最佳参数。通过分析逆变器模型影响输出电压的主要因素,利用BP神经网络建立了系统的逆模型,利用神经网络逆模型对控制器进行补偿,减小负载变化对系统造成的影响。仿真实验结果表明,该方法可以有效地提高光伏逆变器的抗负载扰动能力,从而降低输出电压的谐波含量。本文的下一步工作是考虑在该系统的基础上进行逆模型的在线训练与更新,从而对更多情况下的系统进行较好的适应。
参考文献
[1] LYU Y, LIN H, CUI Y. Stability analysis of digitally controlled LCL?type grid?connected inverter considering the delay effect [J]. IET power electronics, 2015, 8(9): 1651?1660.
[2] RAHMANI B, LI W, LIU G. An advanced universal power quality conditioning system and MPPT method for grid integration of photovoltaic systems [J]. International journal of electrical power & energy systems, 2015, 69: 76?84.
[3] ABO?AL?EZ K M, ELAIW A, XIA X. A dual?loop model predictive voltage control/sliding?mode current control for voltage source inverter operation in smart microgrids [J]. Electric power components and systems, 2014, 42(3): 348?360.
[4] HUANG H, HU R, YI G. Research on dual?loop controlled grid?connected inverters on the basis of LCL output filters [J]. Electronics & electrical engineering, 2014, 20(1): 8?14.
[5] KIREE C, KUMPANYA D, TUNYASRIRUT S, et al. PSO?based optimal PI(D) controller design for brushless DC motor speed control with back EMF detection [J]. Journal of electrical engineering & technology, 2016, 11(3): 715?723.
[6] DHUMALE R B, LOKHANDE S D. Neural network fault diagnosis of voltage source inverter under variable load conditions at different frequencies [J]. Measurement, 2016, 91: 565?575.
[7] CALVINI M, CARPITA M, FORMENTINI A, et al. PSO?based self?commissioning of electrical motor drives [J]. IEEE transactions on industrial electronics, 2015, 62(2): 768?776.
[8] GARG H. A hybrid PSO?GA algorithm for constrained optimization problems [J]. Applied mathematics and computation, 2016, 274: 292?305.
[9] SHI Y, EBERHART R. A modified particle swarm optimizer [C]// Proceedings of IEEE International Conference on Evolutionary Computation. Anchorage: IEEE, 2002: 69?73.
[10] ABDULLA P A, ARONIS S, ATIG M F, et al. Stateless model checking for TSO and PSO [C]// Proceedings of International Conference on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2015: 353?367.
[11] ZAREMBA W, SUTSKEVER I, VINYALS O. Recurrent neural network regularization [C/OL]. [2015?02?19]. https://arxiv.org/pdf/1409.2329.pdf.

