基于 SVM 预测模型的工程初设阶段概预算研究★

高 淑 玲

(北京国信鑫业工程咨询有限责任公司，北京 100011)

0 引言

由于设计人员考虑安全因素或采用新技术，设计预算通常超过前期审定的投资额，因此对于投资方和设计方来说，在设计过程中如何快速准确的控制造价超支现象的工程造价预测方法显得尤为重要[1，2]。由于在设计阶段各类工程信息匮乏，导致对造价预测存在困难，因此对工程初期设计阶段的工程造价预测缺乏较为有效的预测方法[3]。

国内外研究学者对工程初期设计阶段的工程造价进行了较为深入的研究。Arafa等基于人工神经网络(ANN)提出了一种基于在完全学习训练样本后提取工程项目的主要特征参数和重新确定内部存储权重的新思路，从而达到在项目信息不完整的情况下估计设计阶段的总造价[4]；Hong从粒子群理论入手针对BP神经网络算法进行了进一步的改进，对于模型的初始权重以及各个阶段的阀值进行了深入的优化[5]。然而上述被优化的算法均对训练样本有很大的需求，并且训练速度很慢[6，7]。因此，本文通过对支持向量机(SVM)进行改进从而得到一种最小二乘支持向量机的算法模型，进而对工程初设阶段造价进行较为详细、全面的预测。

1 基于工程特征选取合适的指标体系

本文运用SVM方法进行预测，当对造价进行预测时，指数的提取处于首要地位，指数是SVM模型的最初输入量的基础。数据采集结束后，对数据进行处理学习，最终实现造价预测的目的。

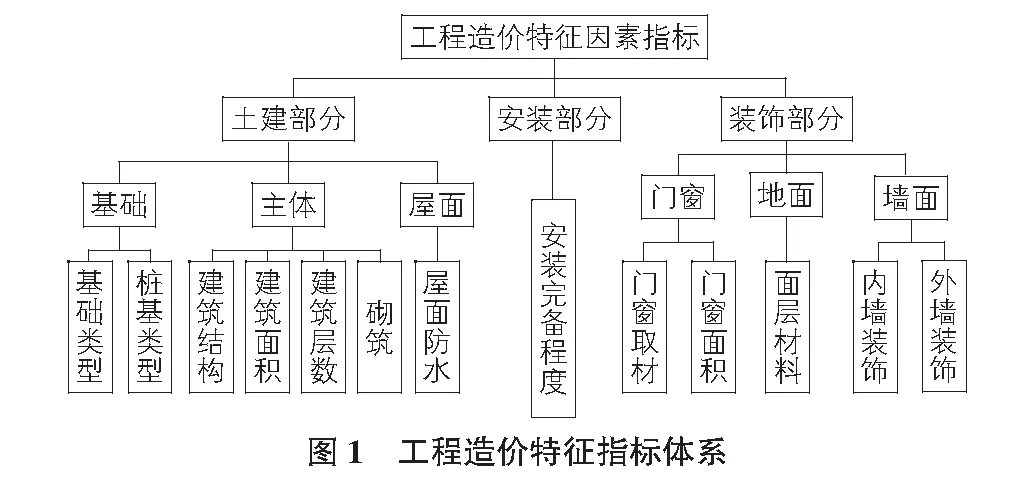
工程造价预测指标是准确预测各种项目造价的基础，并对各个方面的特点进行全面、准确的反映。工程的总造价由许多部分组成，并且各个部分所占的权重不同，根据这一现状可以形成工程造价特征因子独有的指标体系。预测的过程出现在项目各个早期阶段，并选择占项目总成本较大比例的对象进行分析[8，9]。土建、装饰以及安装工程是民用工程建筑的主要方面，其中土建工程在建筑造价中处于最重要的地位，装修和安装工程在造价中处于次要地位。主要研究分析土建工程中的基础、主体和屋顶等多个特征类别，并适当考虑装饰工程和安装工程中的门、窗、地板和墙面等不同特征因素。通过对建筑工程造价结构进行深入的研究，得出能够详细反映建筑工程的造价结构的特征因素(如图1所示)。

土建部分、安装部分以及装饰部分与工程造价的相互关系如下[10，11]：对于基础而言，基础类型的差异导致了钢筋和混凝土的使用数量存在明显的不同，这对工程造价有很大影响，对于一些基础面积较小的高层建筑，尤其是沿海软弱土层，桩基是不可缺少的基础；对于主体部分而言，结构类型的选择直接决定了建筑物的总造价，目前我国主要结构形式有框架结构、框架—剪力墙结构、钢结构等三种常用类型；建筑面积和楼层数的不同使得建筑物的柱、梁、板的选择存在明显差异，而这方面对建筑总造价的影响占较大比重；在总工程量中，砌筑工程占据很大比例，砌筑材料的种类与数量决定了总造价的高低；屋顶的防水做法和防水材料的选择直接决定屋顶部分的总造价；门窗的材料有铝合金，塑钢，胶合板等，其成本与门窗形式和材料均有直接联系；面层材料对楼地面的影响尤为重要。不同的面层材料导致不同的面层施工工艺，进而导致不同的造价；内墙和外墙的装饰材料是占墙面成本的主要因素。

2 基于SVM建立造价的预测模型

2.1 对样本的数据进行规范化处理

工程特征指数(X1～X13)中存在定量与定性的差异。通过对特征指数进行量化的方式得到更好的预测流程，量化标准如表1所示。为了得到更加均匀与收敛的输入和输出数据，需要对样本的数据进行归一化处理，并将值的大小限定在[0，1]范围内。对极值线性的归一化方法进行优化，将其权重值确定为0.8，并加入系数值0.1，如式(1)所示。

(1)

其中，xnorm为进行预处理后得到的数值；x为最原始的数据值；xmin为在工程特征指数下所取得的最小值；xmax为在工程特征指数下所取得的最大值。

表1 工程特征量化标准

2.2 建立模型并确定相应的参数

对于训练方面的误差以及体验方面的误差，RBF核函数在这两方面存在显著的优势，因此基于RBF核函数建立合理的关于工程造价预测方面的SVM模型，即：

(2)

为了将误差控制在合理的范围内，将正规化的参数b的数值为10，核函数的宽度系数σ2的数值为30。

2.3 基于SVM法预测模型的学习和收敛

基于历史数据对SVM法预测模型进行训练后再进行数据测试。当SVM预测模型预测值与实际值之间的误差不大于10%时即认为该模型的收敛精度较高可以直接用于实际工程造价应用。

3 实例案例

3.1 关于原始指标进行规化的数据获取

从某房建项目中选取已经完工的15个成品住宅项目，编号A1～A15，并且从项目中提取出实际的数据，并对数据进行指标化。对采集的原始数据进行合理量化，并对原始数据进行计算后得到标准化的数据，详见表2，表3。

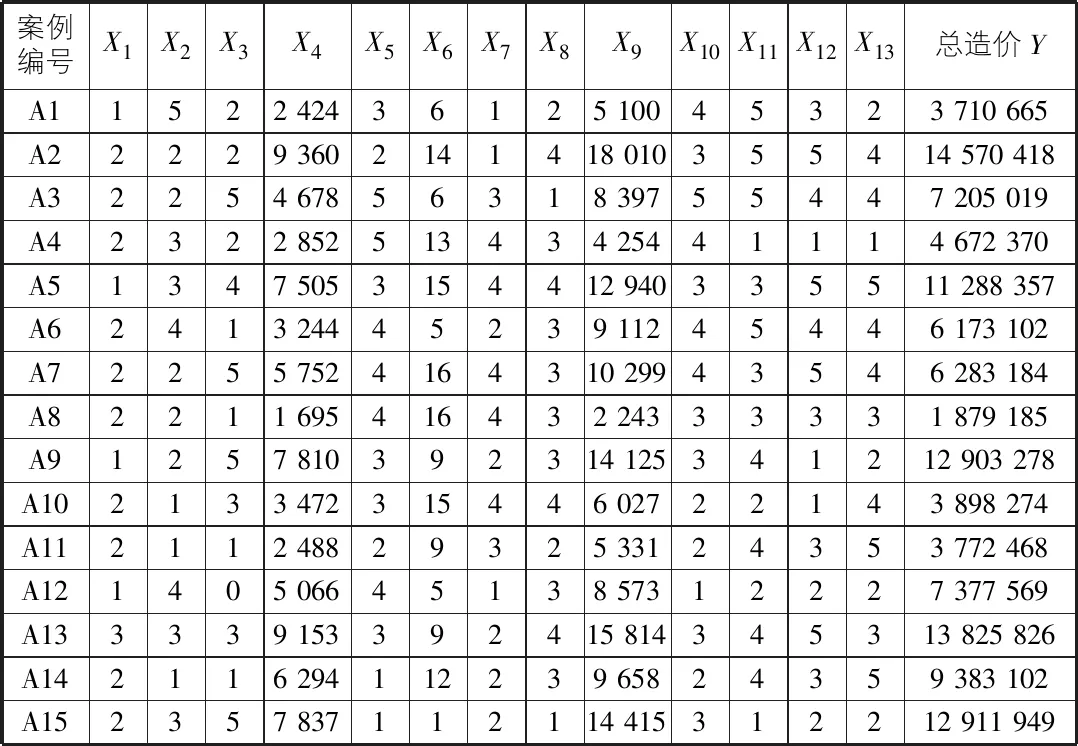
表2 样本原始数据

表3 标准化后的样本数据

3.2 运用SVM建立的模型进行测试

从已建成的15个成品住宅项目中，选取11组数据作为样本数据用于模型的训练学习，剩余的4组数据用于校核训练模型。通过对这15组数据进行处理得出决策函数和参数值，并使用Matlab进行程序编程。通过模型测定出预测的数值与实际采集到的数值差距，详见图2,图3。

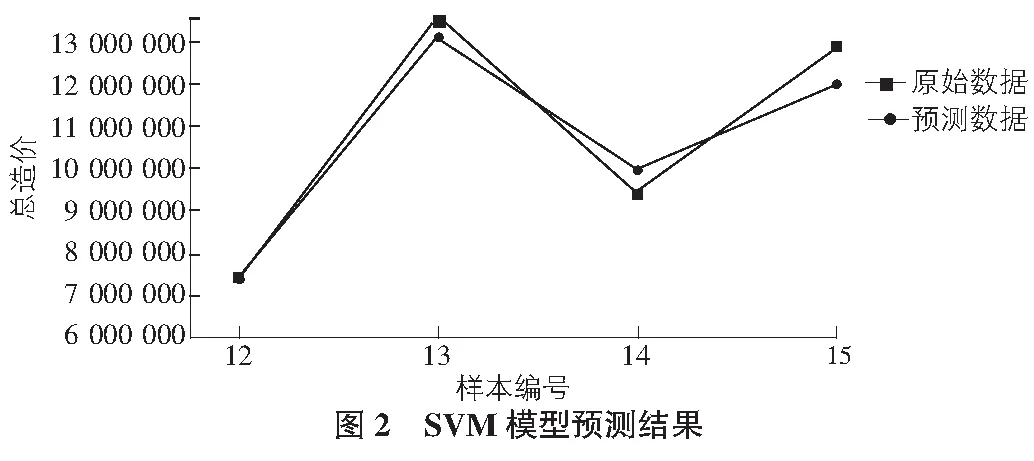
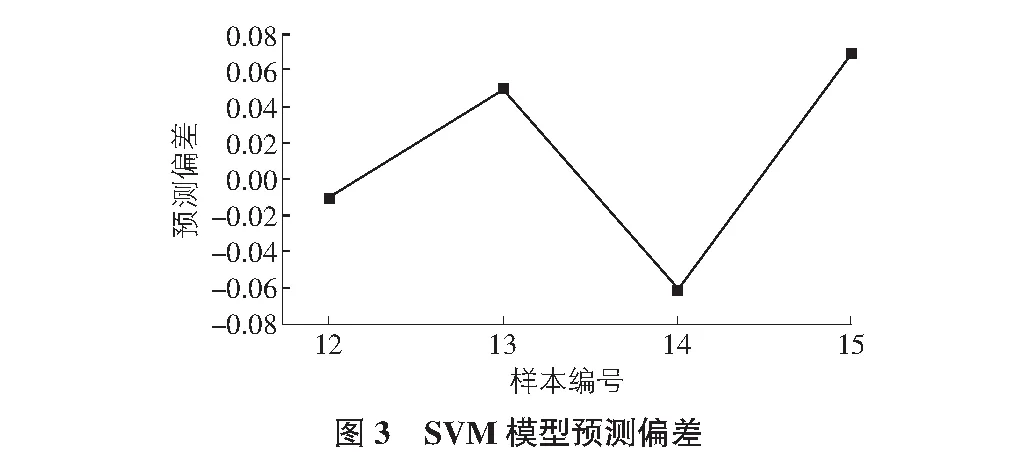
由图2，图3，基于SVM预测模型测定出剩余4组成品住宅项目的预测数值与实际采集到的数值差距对比结果可知，预测偏差发生在第15组成品住宅项目中，原始数据与预测数据分别为12 911 948.94元和12 008 112.51元，最大误差值为7%，小于误差最大允许值10%，误差精度满足要求，说明该SVM预测模型可为工程初设阶段概预算提供参考价值。

4 结语

为了提高建筑工程初期设计阶段的工程预测可靠性，本文在国内外学者研究成果的基础上，通过对支持向量机(SVM)的改进从而得到一种最小二乘支持向量机的算法模型(SVM预测模型)，进而实现对工程初设阶段造价进行较为详细、全面的预测。并以某房建项目中选取已经完工的15个成品住宅项目为工程依托将SVM预测模型进行应用，实际数据中最大误差值为7%小于误差最大允许值10%，误差精度满足要求，说明本文提出的SVM预测模型可为工程初设阶段概预算提供参考价值。