高原寒冷地区曲线梁桥的支座受力分析

马清祥 海显勋

(1.青海交通投资有限公司，青海 西宁 810001； 2.青海交通职业技术学院，青海 西宁 810001)

1 概述

桥梁上部结构和下部结构通过桥梁支座连接成一体，使得来自上部结构的荷载通过桥梁支座传递给下部结构，因此支座的质量和性能对桥梁的使用性和耐久性产生直接影响。有关的理论分析与计算表明，支座的稳定性与支座形状参数、橡胶物理性能、支座水平变位和竖向荷载等多个因素有关，且在不同参数取值范围内有很大变化，所以对不同的支座，为保证其稳定性，适宜采用不同的水平变位和竖向压力的限值。基于此，本文以高原寒冷地区曲线梁桥为研究对象，展开曲线梁桥支座受力分析研究。

2 曲线梁桥的支座受力计算

2.1 桥梁概况

对大武至久治公路门堂大桥(曲线梁)桥梁支座的受力性能进行分析。计算模型计算参数：钢筋混凝土箱梁桥，C50混凝土，桥梁跨度为：5×20 m连续箱梁，桥梁宽度为17.5 m，桥梁的弯曲半径为600 m。设计荷载为公路—Ⅰ级车辆荷载，设计车道两车道，计算车道荷载为均布荷载10.5 kN/m，集中荷载300 kN，支座采用圆板式橡胶支座，型号为d350×63 mm。

2.2 曲率半径600 m模型计算

采用Midas/Civil 进行有限元分析，每个墩台上设2个支座，用梁单元来模拟梁体受力状态，取单箱梁进行支座受力分析。共有节点49个，单元42个，橡胶支座采用弹性连接进行模拟，根据剪切模量和尺寸、形状系数计算出各个方向的刚度值。曲率半径为600 m的桥梁模型如图1所示。

本文考虑车辆中载和偏载两种工况，计算分析各工况下的支座反力以及梁体的内力、位移值。计算结果如图2～图5所示。

各支座的反力计算结果如表1所示。

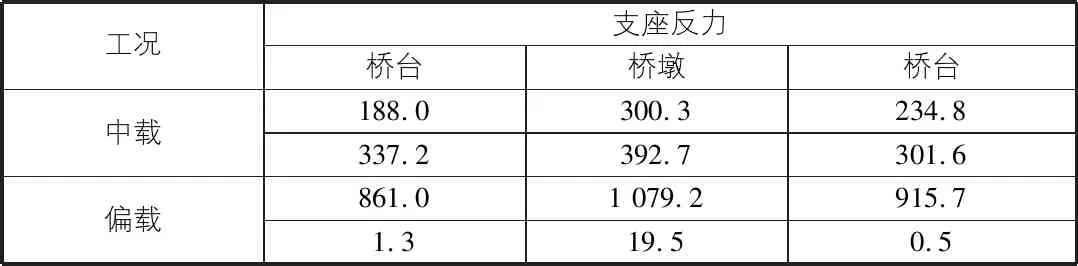
表1 墩台支座反力表(曲率半径600 m) kN

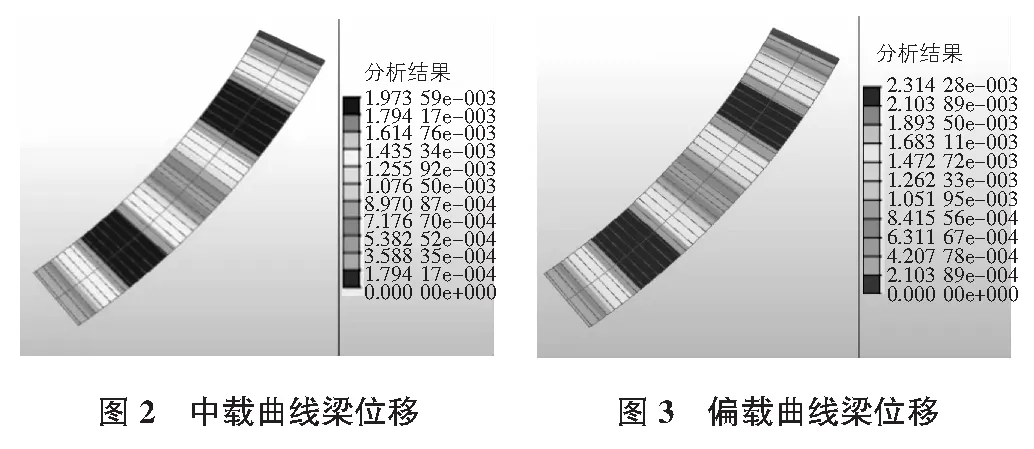
从图2～图5及表1可以看出，曲率半径为600 m时，支座的横向和纵向受力表现为不均匀性，且外侧弧与内侧弧位置的支座的反力差值较大。对称加载情况下，外弧反力为内侧弧的1.28倍～1.79倍；偏载时反力差值更大，梁体反力基本由单个支座支撑。梁体在外侧弧的位移值及弯矩值都比内侧的稍大，这将在梁体内产生扭矩，进一步加剧内外弧支座反力的不均匀。

2.3 曲率半径800 m模型计算

曲线梁桥的曲率半径增大到800 m后，其他条件不变，各支座反力的计算情况如表2所示。

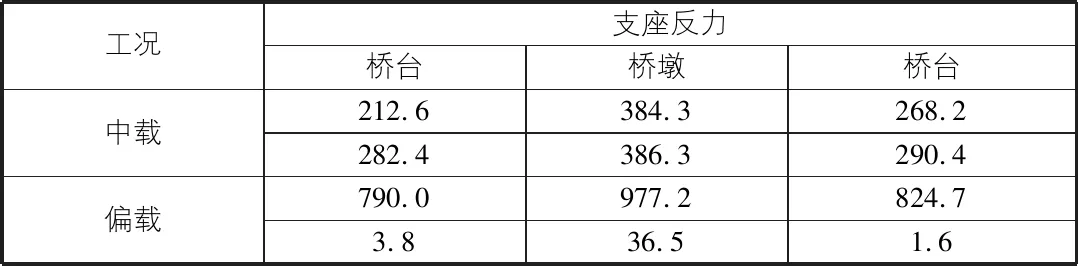
表2 支座反力表(曲率半径800 m) kN

由表2可知，曲率半径增大到800 m后，桥梁墩台内外侧支座反力大小差值有减小趋势，对称加载时，外弧反力为内侧弧的

1.10倍～1.33倍；偏载作用时，支座反力分配差异仍旧明显，内侧反力值很小，梁体与支座间可能脱空。由计算结果可知，曲率半径为800 m梁体的位移和弯矩的内外侧差值对比曲率半径为600 m时有所降低。

2.4 曲率半径1 000 m模型计算

曲率半径增大到1 000 m时，曲线桥在荷载作用下的各支座反力的计算值如表3所示。

表3 支座反力表(曲率半径1 000 m) kN

从上述结果可见，曲率半径为1 000 m时，各墩台内外侧支座的反力值在中载的情况下均较接近。偏载时支座受力和直线桥梁类似，弯矩和变形图也与直线桥情况一致，这说明曲线梁桥的支座受力在曲率半径达到1 000 m时与直线梁桥较为接近。

3 结语

本文从高原寒冷地区实际情况出发，选取曲线桥梁的支座进行受力分析研究，相关研究结论如下：

随着曲率半径的增大，曲线梁桥外侧支座的反力逐渐减小，内侧支座的反力呈增大的趋势。梁端支座的反力随曲率半径的增大也逐渐减小；当曲率半径为600 m时，支座在横向和纵向受力都不均匀，外侧弧位置的支座的反力与内侧弧支座的反力差值较大；曲率半径为800 m时，墩台内外侧支座的反力差值有减小趋势；曲率半径为1 000 m时，各墩台内外侧支座的反力值均较接近。