基于回归分析的隧道收敛预测★

何应鹏 王 娜 李璇琼

(四川建筑职业技术学院，四川 德阳 618000)

1 概述

随着我国基础设施建设的快速发展，大量的隧道地铁被兴建起来，极大的提高了通行效率。由于施工技术的进步，加上较高的经济效益与便捷性，隧道地铁正越来越多的被建设于各类交通工程。隧道工程由于其本身的性质，其周边地质环境一般较为复杂，建设期间不确定因素多，导致隧道工程的事故率相对较高且事故损失一般也较大，故需要在隧道的建设及运营期间对其进行变形监测，了解隧道的状态，以保证隧道的安全。隧道工程的变形监测有很多指标，精度要求也较高，其中很重要的一项指标就是隧道的净空收敛值。净空收敛即隧道初支两侧边墙同一高程的水平距离变化，由周边土体的挤压力产生。正常情况下隧道建设过程中都会产生收敛，但收敛值不能超过一定限度，超过规范的规定则可能会影响隧道的使用安全。综上所述，在建设及运营期间对隧道的净空收敛值进行监测及对其收敛状态进行分析与预测是一项必不可少的内容。

对隧道的收敛状态分析，目前有多种方法，回归分析是主要的方法之一。回归分析分为线性回归和非线性回归，线性回归对应线性关系，指自变量和因变量之间的关系为一条直线，非线性回归对应非线性关系，指自变量和因变量之间的关系为曲线。对于隧道的收敛值来说，随时间的增加一般都呈现非线性的曲线，使用非线性回归分析拟合精度相对更高。通过非线性回归分析可得到回归公式，再由回归公式可预测后期的收敛值，为施工及运营做出指导，提前做出相应预案，保证隧道的安全。本文通过实例，将隧道收敛的实测值与回归公式预测值进行对比，得出预测效果良好。

2 回归分析原理

回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。此外，根据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析，线性回归分析是基本的分析方法，非线性回归可以通过数学方法转化为线性回归处理。

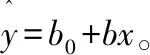
回归预测模型是否可用于实际预测，取决于对回归预测模型的检验和对预测误差的计算。回归方程只有通过检验，且预测误差较小，才能将回归方程作为预测模型进行预测。对于可选用回归方程形式，需要加以比较以选出较好的方程，常用的准则有：

1)决定系数R2：R2=1-SSE/SST。

R2称为决定系数，R2≤1。R2大表示观测值与拟合值比较靠近，因此R2较大的方程拟合效果好。

s称为剩余标准差，可以看成是平均残差平方和的算术根，其值小的方程拟合效果好。

决定系数R2和剩余标准差s对于所选方程总是一致的，因为s小则残差平方和小，从而R2必定大。R2的大小给出了总体上拟合程度的好坏，s给出了观测点与回归曲线偏离的一个量值。所以，通常在实际问题中两者都求出，从不同角度去认识所拟合的曲线。

3)F检验：F=(SSR/1)/[SSE/(n-2)]。

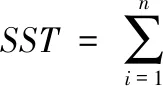
3 隧道收敛分析与预测

本文以某公路隧道连续55期监测数据为例，分析收敛值随时间增加的变化规律，并对收敛值做出趋势预测。隧道水平收敛点布置示意图如图1所示。

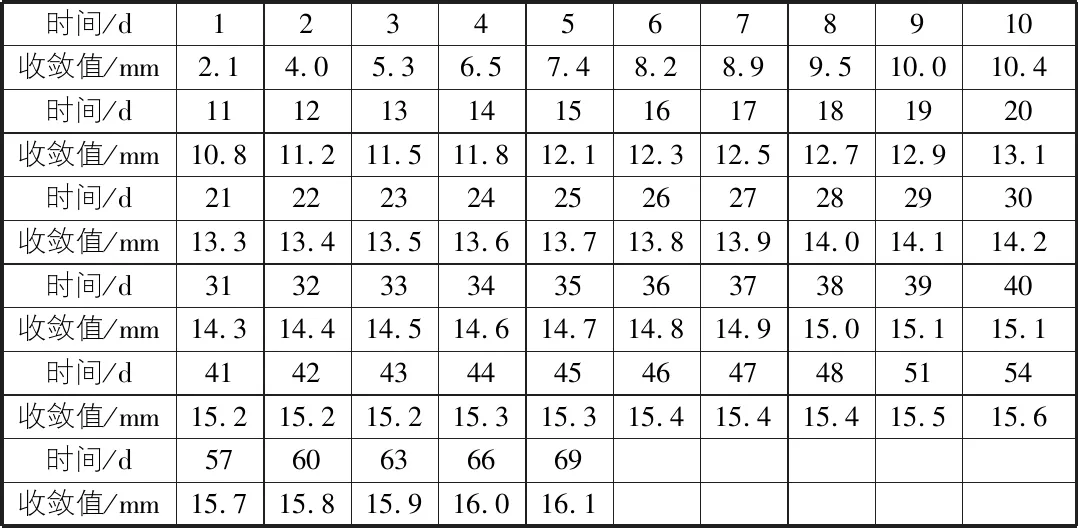
隧道不同断面处的收敛值不同，断面数据较多，为方便分析，取隧道中部较有代表性的一处断面水平收敛值为例，具体收敛数据如表1所示。

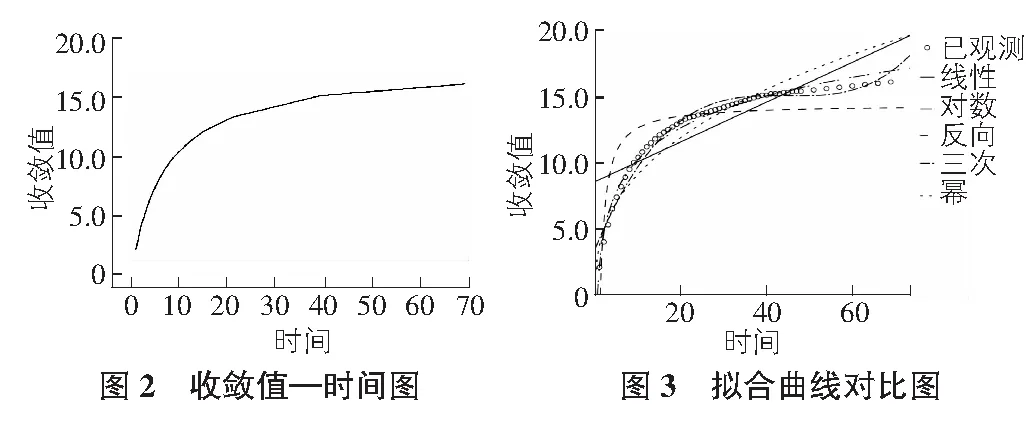
根据表1中该断面连续55期的收敛值，绘制收敛值—时间图，见图2。

根据图2可知，收敛值随时间的增加而增加，呈现先快后慢逐渐趋于稳定的趋势，符合正常的隧道收敛过程。收敛值与时间呈现曲线关系，使用非线性回归分析更为准确，选择SPSS中常用非线性函数进行拟合，并同线性拟合进行对比，拟合程度见图3。

表1 时间序列的水平收敛数据

时间/d12345678910收敛值/mm2.14.05.36.57.48.28.99.510.010.4时间/d11121314151617181920收敛值/mm10.811.211.511.812.112.312.512.712.913.1时间/d21222324252627282930收敛值/mm13.313.413.513.613.713.813.914.014.114.2时间/d31323334353637383940收敛值/mm14.314.414.514.614.714.814.915.015.115.1时间/d41424344454647485154收敛值/mm15.215.215.215.315.315.415.415.415.515.6时间/d5760636669收敛值/mm15.715.815.916.016.1

常用非线性函数拟合和线性拟合精度指标如表2所示。

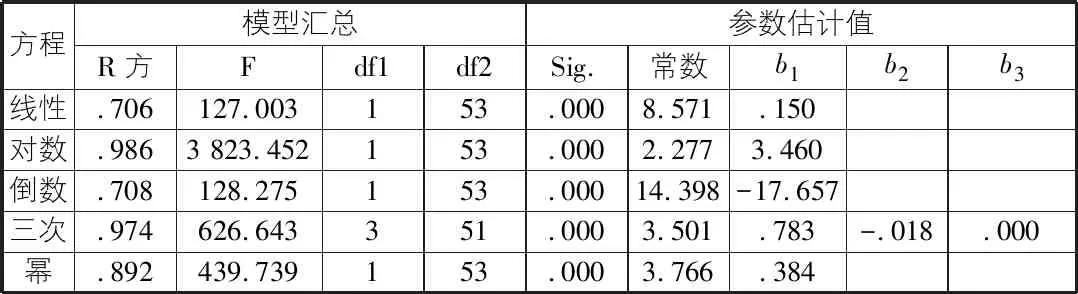
表2 拟合精度指标表

自变量为时间。

根据表2，常用的非线性函数中，对数函数的R方为0.986，倒数函数的R方为0.708，三次多项式函数的R方为0.974，幂函数的R方为0.892，均高于线性拟合的R方0.706，证明非线性拟合较线性拟合精度更高。对于本文所选断面收敛值，使用对数函数拟合效果最好，回归公式为：y=2.277+3.46lnx，对数拟合程度见图4。对数函数拟合检验精度如表3所示。

根据对数拟合的回归公式y=2.77+3.46lnx，预测第72 d,75 d的收敛值为17.07 mm,17.22 mm。实测第72 d,75 d的收敛

值分别为16.2 mm和16.3 mm，对比结果见表4。

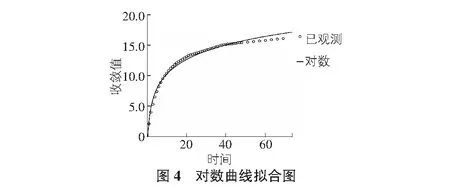
表3 对数拟合检验精度表

参数平方和df均方FSig.回归541.2311541.2313 823.452.000残差7.50253.142总计548.73354

表4 预测值与实测值对比表

根据表4可知，预测收敛值与实测值差值较小，预测结果较为准确。通过图3，图4，表2～表4表明，非线性的对数拟合方法能较精确的模拟隧道的收敛变化规律，且能做出较准确的收敛趋势预测。

4 结语

为保证隧道在建设与运营期间的安全，必须对其进行高精度变形监测，其中重要的一项即净空收敛值，通过收敛值反映隧道的受力变化，了解其安全状态。本文通过实例，得到专业仪器测量的收敛值后，使用数学软件SPSS对隧道收敛值进行回归分析，掌握隧道的收敛变化规律，预测其收敛趋势，得出以下结论：

1)回归分析方法可以用于隧道的净空收敛规律分析，通过掌握隧道的净空收敛状态，保证隧道在建设及运营期间的安全。

2)隧道的净空收敛值与时间存在非线性的对数函数关系。

3)通过回归分析方法可以预测隧道接下来的收敛值，通过与实测收敛值的对比，得到预测效果良好。