让数学思想的光芒闪耀课堂

尹志淑

数学思想方法是对数学知识、数学规律本质的认识。学生只有掌握了数学思想方法，才能真正掌握数学的通性、通法，从本质上把握数学，从而有效地应用知识、形成能力。因此，在数学教学中，教师应让学生感受数学思想方法的奇妙，受到数学思维的训练，逐步形成严谨地思考问题的意识。

一、感悟概念，而不是简单地出示定义

数学概念是数学思维的基础，是感性认识上升到理性认识的结果。这一结果的实现要经历观察、分析、类比、抽象、概括等思维过程，并依靠数学思想方法的指导。因此，概念教学应以典型的实例为载体，引导学生通过观察、分析揭示概念的本质特征，归纳概括出概念。在这个过程中，教师要引导学生感悟数学思想方法。

例如，教分式的概念时，可分下面几步进行。

1.老师买15本书花了237元，每本书多少钱？

2.若花了a元买了15本书，每本书多少钱？

3.若花了237元买了b本书，每本书多少钱？

4.若花了m元买了n本书，每本书多少钱？

5.若花了137元买了5本书，又花了x元买了y本书，平均每本书多少钱？

二、注重过程，而不是草率地得出结论

数学教学过程中，教师应将概念等结论性知识设计成再发现、再创造的过程，引导学生对数学定理、公式、法则等进行探究。学生在探究的过程中，弄清楚结论的来龙去脉，领悟其中蕴含的数学思想方法，发展推理能力。

例如，在推导余角与补角的性质时，由于补角的性质可由余角的性质类比得出，教学的重点应该是余角的性质的证明。而余角的性质有两个命题：同角的余角相等和等角的余角相等。因此，这一环节可以设计两个活动。

接下來补角的性质，学生可以类比余角的性质的证明方法得出结论。这一教学过程，既让学生经历了合情推理和演绎推理的过程，又渗透了符号思想、类比思想。

三、构建框架，而不是简单地罗列知识

对某个章节知识的复习教学，教师在梳理本章的知识时，要注重揭示新旧知识之间的内在联系和数学思想方法的应用。教师可以引导学生运用类比、化归、分类等方法理清知识点的来龙去脉，构建知识和数学思想方法框架。

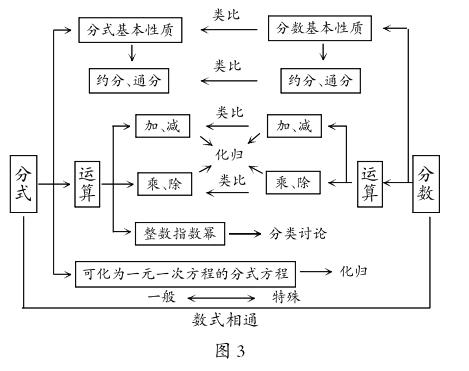
例如，在复习分式时，分式这一章包含了许多数学思想，如类比思想：分数与分式定义的类比，基本性质的类比，运算顺序和运算方法的类比等；化归思想：异分母分式加减运算，解分式方程等都用到了化归思想；还有分类思想、整体思想等。在章节总结时，教师可以引导学生清晰地构建知识和数学思想方法的框架图（如图3所示）。

四、提炼反思，而不是做一题会一题

反思是数学活动的核心和动力。在解题教学中，学生解题后，教师应引导学生进行解题后的反思。比如，解法是怎样想出来的？哪一步是关键？这个方法能推广吗？能否找到更好的解题途径？如何提炼解题的基本方法？等等。这样的反思，有利于学生养成反思的习惯，做到解一题而通一类。

例如，学完等腰三角形的性质和判定后，有一节习题课是探究与等腰三角形有关的二倍角问题。

探究活动一：如图4，在△ABC中，D是BC延长线上的一点。

随后，教师引导学生提炼出解题的基本方法：一般三角形内角的二倍角关系，可以通过截长补短的辅助线方法构造全等，转化成等腰三角形的外角与底角的二倍角关系。在此过程中，教师层层追问：如何做辅助线？截长补短的目的是什么？为什么在此处截或补？学生在思考的过程中逐步体会蕴含其中的数学思想方法，掌握解题的基本思路。

【本文系湖南省教育科学规划课题“构建学校三本教研体系，提升教师核心素养的实践研究”（课题批准号：XJK17BJSF11）的阶段性研究成果】

（作者单位：娄底市第一中学附属实验学校）