舞台3D威亚系统的力学特性分析

尹海鹏 郭克桥 戴志荣

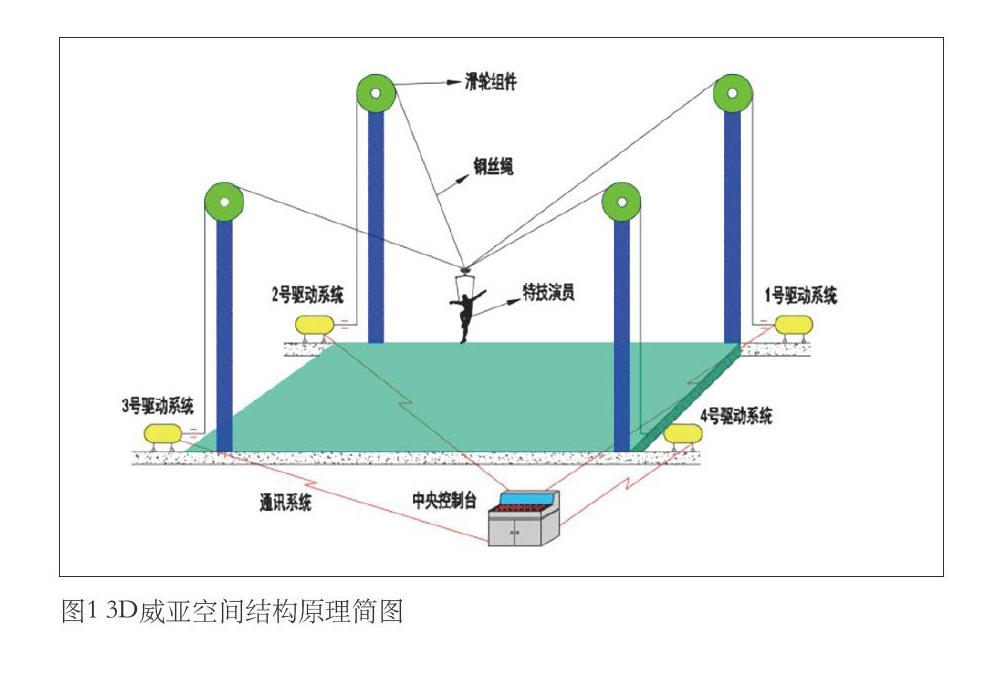
[摘要]介绍3D威亚系统的研究现状，并从理论入手分析3D威亚系统在给定运行区域内的钢丝绳拉力函数。

[关键词]3D威亚系统;力学特性;运行区域;拉力函数

文章编号：10.3969/j.issn.1674-8239.2019.07.009

1引言

3D威亚技术是现代舞台装备领域中较为先进的立体舞台展现新形式之一，通常采用4（或8）套伺服系统独立驱动、集中控制，以使被吊设备或特技演员在给定的三维区域内的任何一点运动，如图1。3D威亚是相对于1D、2D威亚提出的概念，1D威亚仅做上下运动，效果类似单点吊机;2D威亚做某一给定平面内的运动。随着社会科技的发展和文化需求的不断提高，1D、2D威亚的局限性越发明显，3D威亚技术的开发应运而生。

目前，普通的3D威亚技术在国内舞台机械工程中已有应用，八索牵引3D多姿态威亚装备在演艺行业内虽已开发出，但应用较少。已公开的研究文献主要集中在安全性控制方法领域，在力学领域方面研究文献较少。贺虎成等对北京奥运会国家体育场威亚主钢索进行受力分析，并验证结论正确性”，其结构可简化为2D威亚系统。寇帅伟基于ADAMS研究了四索牵引摄像机器人的动力学特性，给出最小二乘解的迭代算法。杨健基于MATLAB研究了四索牵引摄像机器人的稳定性和冗余索力并进行优化。姚蕊、崔传贞对FAST（500m口径球面射电望远镜）系统大跨度六索牵引并联机构力学特性进行了分析，但其结构和适用特点与舞台用3D威亚系统略有差异。笔者针对舞台专用3D威亚装备空间运行力学性能进行分析，并给出结论。

2力学性能分析

2.1力学分析数学模型

根据常规剧场3D威亚装备应用实践，建立数学分析模型。一般情况下，驱动系统对称布置在距地面高度为H的位置，滑轮出绳点在投影面形成的矩形区域为长为L、宽为B（常见L=B，即出绳点落在半径为R的圆弧上）。终端附属设备和特技演员总重为G。设4根牵引钢丝所受拉力为Fi（i=1，2，3，4，下同）与水平面夹角为θi，Fi在XOY平面内投影Fisinθi与坐标轴所成锐角为ψi，悬挂物在允许空间内任意一点的位置坐标为M（x，y，z），如图2所示。

2.2力学分析

为方便研究，对实际工程模型做以下简化假设：（1）受分析的4条钢丝绳规格特性相同，质量不计;（2）钢丝绳为刚性，即不随拉力产生微伸长;（3）出绳点位置不随钢丝绳与滑轮包角的变化而变化。

x方向力学平衡列式：

明显（22）式有無穷解。考虑到模型在运行过程中，3号钢丝绳仅有受拉或松弛两种状态，即0≤F3，F3为任意给定的常数或拉力函数，可通过构造F3的拉力函数，来讨论（22）式的解集。

33D威亚系统结构设计

3.1运行空间分析

为方便，基于以下案例分析。某工程配套319威亚系统装备，要求驱动机安装在距地H=10m的距离，均匀布置在R=13m的圆弧上，参与演出时能满足2人（250kg）及其附属装备（50kg）以v=0.03m/s～3m/s飞行速度飞行，试设计飞行区域并选配电机功率。

设飞行器终端在水平面内的最大区域内运动，即-R≤x、y≤R;根据—般要求钢丝绳与水平面夹角0i≥15°，即运行高度h

3.23号钢丝绳拉力函数构造

构造拉力函数的方法有很多，但其必须遵循的原则是：（1）该钢丝绳最远端拉力值应为O，这样能增大表演空间;（2）钢丝绳拉力差最小，这样既减小了电机功率、节约能源、提高经济性又使结构趋于稳定、便于控制。

易知1号钢丝绳x向受力F1将随3号钢丝绳F3的增大而增大;且F3在z轴任意一点拉力值均不为O，在最远端拉力值应为0，故F3变化必为减函数，否则，随着飞行器终端靠近悬挂点正下方，必然出现F2=F4

4结论

基于假设理论和力学分析，给出3D威亚系统运行区域边界上各钢丝绳拉力求解方法，并得出以下结论：

（1）简化模型下四索并联系统为超静定问题，在z轴和OC上运动时可准确求解钢丝绳拉力值，其他区域和边界上可通过构造拉力函数的方法确定。

（2）飞行器在第一象限1/8区域飞行时构造F3的拉力函数必须为减函数，该函数边界值满足F3Ix=0=F1（o，o，z）时，所有钢丝绳拉力均匀连续平稳，振动较小;边界值满足F3Ix=R=0时，飞行器运行空间最大。

（3）该模型下钢丝绳运行至Oc端点处，钢丝绳拉力最大，运行全区域拉力值包络在该函数曲线之下，故可以此选配电机功率。