正、偏楔形盘形滚刀破岩作业载荷对比研究

张照煌，洪 文，刘 青

（华北电力大学 能源动力与机械工程学院，北京 102206）

1 研究背景

盘形滚刀作为TBM（Tunnel Boring Machine）的关键部件，其破岩性能直接关系到TBM的掘进效率和施工成本。TBM盘形滚刀严格意义上讲已经走过了两代发展历程——1950年代至1980年代的楔形刃盘形滚刀（第一代）和1980年代至今的CCS（Constant Cross Section的英文缩写）型盘形滚刀（第二代）。第一代盘形滚刀设计理论建立的基础是盘形滚刀的压痕试验，其成果也就是盘形滚刀的一维设计理论，如伊万斯（Evans）［1］认为盘形滚刀破岩时垂直力与盘形滚刀压入岩石区域在岩石表面的投影面积成正比，其比值为岩石的单轴抗压强度，从而提出了伊万斯预测公式；盘形滚刀第二代设计理论建立的基础是盘形滚刀线性切割岩石的试验，亦即盘形滚刀的二维设计理论，如Rostami等［2］通过盘形滚刀线性切割岩石的试验提出了科罗拉多矿业学院预测公式；我们项目组［3-4］通过对盘形滚刀的压痕试验进行统计分析，建立了盘形滚刀的垂直力模型并提出了滚刀破岩垂直力计算公式；谭青等［5］采用ANSYS-LS/DYNA建立了盘形滚刀破碎混凝土模型，分析了盘形滚刀圈和混凝土的应力分布，得到应力集中对滚刀失效的影响；张珂等［6］采用ABAQUS三维软件分析了不同切深对滚刀受力的影响；满林涛等［7］依据岩石受力特性和Drucker-Prager塑性屈服准则，采用ABAQUS软件分析不同切深对岩石破碎的影响。随着TBM在我国的广泛应用及其发展，尤其是引输水工程，如万家寨引输水工程、引黄工程和大伙房引输水工程等的应用，TBM盘形滚刀的破岩效能引起了国内外领域学者越来越多的关注。提高盘形滚刀寿命，亦即提高其耐磨性容量，国外学者进行了改进其成型工艺和增大其直径等两个方向的研究。研究发现，通过改进盘形滚刀成型工艺提高其耐磨性容量，成本太高，以至应用单位无法承受；而采用增大盘形滚刀直径的途径增大其耐磨性容量，已获得工程单位的广泛认可并得到了应用。但实际应用发现，盘形滚刀直径增大后，在相同贯入度（侵入岩石的深度）条件下，盘形滚刀所需要的贯入岩石的推力和使其转动的滚动力都需增加，相应刀盘的刚度和强度也需要增大，从而对TBM整机的设计产生重大影响，否则，施工中引起的刀盘振动严重影响TBM的掘进速度甚至威胁刀盘的使用寿命。基于这样的工程背景，通过研究的深入，我们逐渐建立起了“通过减小盘形滚刀破岩过程中的滑移量，提高其耐磨性容量的理念”。这一理念的实施，需要解决两大科学和技术难题：（1）盘形滚刀破岩刃域接岩应力最大的点所在位置；（2）最大应力点的速度矢量。这两大问题的解决，就是我们提出并建立的盘形滚刀三维设计理论，偏楔形盘形滚刀就是这一理论应用的直接成果，具体内容可参见文献［8-10］。若已知盘形滚刀作业对象岩石的性能参数，根据相关理论，可计算出正楔形盘形滚刀刃角φ及刃宽，根据盘形滚刀三维设计理论可计算出偏楔形盘形滚刀内外侧（盘形滚刀向着刀盘旋转轴线的侧面为其内侧，远离刀盘旋转轴线的侧面为其外侧）刃角变化量2α；再根据盘形滚刀结构（如轴承宽度等）特点，可确定其宽度H，根据掘进速度和推力可确定其直径2r。上述参数含义参见图1所示。

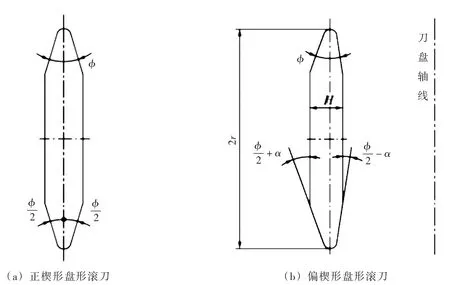
图1 正、偏楔形盘形滚刀外形图

在理论上，偏楔形盘形滚刀破岩的优越性，尤其在耐磨性方面较正楔形盘形滚刀是明显的，但进行物理试验或现场实验验证尚受到诸多技术和物理因素的限制，为此，我们通过理论计算和软件模拟对比，进一步检验偏楔形盘形滚刀破岩的优越性。在理论计算方面，以正楔形盘形滚刀破岩的垂直力和滚动力计算值为基础依据，并与其相对应的模拟值进行对比，模拟采用软件ABAQUS并对正、偏楔形盘形滚刀在不同安装半径和不同切深条件下的载荷进行对比分析；若模拟结果显示，在相同盘形滚刀半径和相同贯入度条件下，偏楔形盘形滚刀的垂直力、滚动力和侧向力均较正楔形盘形滚刀为小，则说明偏楔形盘形滚刀具有较好的破岩效果——破岩力小，但贯入度相同。破岩力小，自然摩擦力也小，从而破岩过程中的磨损也小，这就间接证明偏楔形盘形滚刀较同直径的正楔形盘形滚刀具有相对高的耐磨性容量，此即我们撰写此论文的目的。

2 模型参数确定

ABAQUS是具有强大功能的工程模拟有限元软件，其解决问题的范围非常广，从简单的线性分析到复杂的非线性分析。ABAQUS中还有丰富的材料模型库，包括金属、橡胶、高分子材料、复合材料、钢筋混凝土、可压缩超弹性泡沫材料以及土壤和岩石等地质材料。所以，本文采用ABAQUS软件对滚刀破岩过程进行分析。

17寸正楔形盘形滚刀圈基本参数见表1所示。根据笔者项目组提出的盘形滚刀三维破岩理论［11］并设计的新型偏楔形盘形滚刀在刀盘上不同安装半径的偏楔形盘形滚刀的内角和外角值见表2所示。

表1 正楔形盘形滚刀参数

盘形滚刀的材料一般为硬质合金钢，其材料参数见表3所示，在模型中将滚刀定义成刚体。

表2 偏楔形盘形滚刀不同安装半径的内、外角

表3 刀圈材料参数

岩石材料模型对盘形滚刀破岩的影响巨大，其核心在于其本构关系和具体参数的选择。岩石破碎过程十分复杂，其本构关系为非线性性质。ABAQUS软件中扩展Drucker-Prager弹塑性模型主要是对岩石材料进行仿真，故采用扩展Drucker-Prager弹塑性模型对破岩进行模拟研究。假设岩石具有各向均匀、同性且连续变形特性。

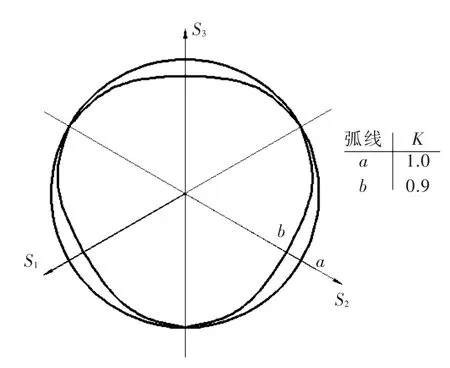
图2 子午线为线性D-P模型在π平面上的形状

扩展线性D-P模型的屈服面如图2所示，岩石屈服曲线函数［11］取为：

其中：

式中：r为偏应力第三应力不变量；P为平均压应力；β为摩擦角；d为凝聚力（与输入的硬化参数有关）；K为材料参数，0.778≤K≤1.0；q为等效压应力。t为偏应力参数，可以由不同的应力状态来确定，如拉应力状态和压应力状态等（a、b分别表示拉伸、压缩强度不同对屈服面的影响，K=1.0时为曲线a，K=0.8时为曲线b）。

岩石样本采用北京昌平花岗岩，其参数［12］见表4。

表4 岩石材料参数

盘形滚刀与岩石之间的装配如图3所示，图中点RP1为刀盘中心点，即盘形滚刀的回转中心。点RP2为盘形滚刀的中心点。盘形滚刀破岩时一方面绕点RP1“公转”，另一方面又绕着自身中心点RP2在岩石表面滚动。

图3 盘形滚刀与岩石装配图

在分析步模块中选择“动力，显示”分析步并设置破岩时间为0.2s。在历程输出模块中，选择输出的参数为“接触”。为了提高盘形滚刀破岩时力与时间的关系，设置输出点个数为300。在场输出模块中可以选择输出“应力、应变、位移”等参数。在相互作用模块中，由于盘形滚刀与岩石的接触为面与面非线性接触，故设置盘形滚刀表面为主动面，设置岩石体为从动面，定义为面与面接触。摩擦公式设置成“罚”，定义摩擦系数为0.3，选择力学约束公式为“罚接触方法”。在约束模块中设置盘形滚刀为刚体并设置刚体的参考点为盘形滚刀的中心点。将盘形滚刀中心点与刀盘中心点设置成铰连接，滚刀转动时即能绕刀盘转动又能绕自身轴线转动。在绝对坐标原点设置铰连接绕Z轴的转速为0.5652rad/s，其它方向的转速为0。

3 仿真结果分析

盘形滚刀表面与岩石接触并相互作用，岩石对盘形滚刀表面的作用力经过刀圈、刀体、轴承最终传递到刀轴上。由于在仿真中将滚刀设置成刚体并等效于RP2点，因此在后处理中查看RP2点的载荷为滚刀所受载荷。

盘形滚刀破岩结果如图4所示。

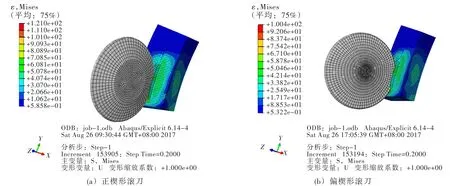
图4 盘形滚刀破岩结果示意图

以安装半径为1500mm、切深为10mm的正、偏楔形盘形滚刀破岩为例，其破岩载荷见图5所示，其中（a）～（c）分别为正楔形盘形滚刀所受垂直力、侧向力和滚动力的时间历程曲线，（d）～（f）分别为偏楔形盘形滚刀所受垂直力、侧向力和滚动力的时间历程曲线。

3.1 理论结果与仿真结果对比由于全断面岩石掘进机盘形滚刀作业对象岩石特性的离散性、各向异性及其复杂性，所以关于盘形滚刀破岩力的预测理论也较多，不下十数套，其中，罗科斯巴勒预测理论在领域内得到了广泛认可［12-13］，其盘形滚刀破岩力预测理论相应公式为：

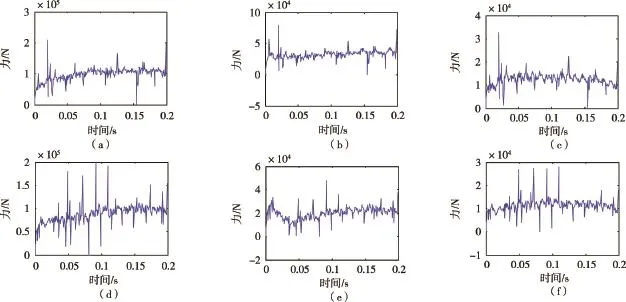
图5 R=1500mm载荷图

式中：FV为盘形滚刀垂直力；Fr为盘形滚刀滚动力；D为盘形滚刀直径；h为盘形滚刀切深；σc为岩石抗压强度；θ为刀刃角。

计算出正楔形盘形滚刀在切深10mm工况下破岩北京昌平地区花岗岩的垂直力和滚动力（取滚刀破岩刀间距S为78mm），得：

为了与预测公式计算出的载荷进行对比分析，将图4仿真的垂直力、侧向力和滚动力的时程曲线求平均值，计算出正、偏楔形盘形滚刀在切深为10mm的平均载荷，见表5所示。

表5 盘形滚刀不同安装半径下破岩平均载荷

为证明仿真结果的可信性和可行性，以罗科斯巴勒预测理论公式的计算值为基础依据，则仿真结果的相对偏差ε为：

式中：F′为盘形滚刀破岩力仿真值；F为根据式（3）、式（4）计算的盘形滚刀破岩力。

将计算出的仿真垂直力和侧向力分别与罗科斯巴勒预测理论公式的计算值进行对比，即：将仿真值和计算值分别代入式（7），得垂直力仿真相对偏差ε1和滚动力仿真相对偏差ε2分别为：ε1=12.6%，ε2=2%。

由此可以看出，垂直力仿真值与罗科斯巴勒预测理论公式的计算值的相对偏差为12.6%，侧向力仿真值与罗科斯巴勒预测理论公式的计算值的相对偏差仅为2%。产生这样偏差的原因除仿真模型与罗科斯巴勒预测理论公式建立用模型存在差异外，“仿真”采用的是盘形滚刀圆形滚压破碎岩石（盘形滚刀实际破岩情形），而罗科斯巴勒预测理论公式建立的基础是盘形滚刀线性滚压破碎岩石的试验，因此，存在上述偏差实属正常，也因此证明了文中所建模型及进行的仿真及其结果的可信性和可行性，仿真结果为正、偏楔形盘形滚刀垂直力、侧向力和滚动力的对比分析提供了依据。

用εF表示偏楔形盘形滚刀破岩过程中的垂直力、侧向力和滚动力与正楔形盘形滚刀破岩过程中的垂直力、侧向力和滚动力之间的相对偏差，则：

将表5中的相应数据代入式（8），计算出正、偏楔形盘形滚刀的垂直力、侧向力和滚动力的相对偏差分别为：εFV=8.0%，εFV=34.8%，εFV=1.7%。

对比正、偏楔形盘形滚刀的破岩力发现，偏楔形盘形滚刀所受的垂直力和侧向力比正楔形盘形滚刀所受的垂直力和侧向力小，其中垂直力减小的相对量为8.0%；侧向力减小的相对量为34.8%；滚动力减小的相对量为1.7%。

3.2 不同安装半径载荷对比分析根据滚刀仿真载荷时间历程曲线，计算出正、偏楔形盘形滚刀在切深10mm时破岩0～0.2s时间内不同安装半径下的平均载荷见表6。

不同安装半径的盘形滚刀所受的平均载荷可以显示出盘形滚刀在不同安装半径下的受载特点。正、偏楔形盘形滚刀在不同安装半径下的受载折线图和载荷相对减小量折线图分别如图6、7所示。

表6 滚刀不同安装半径下的平均载荷

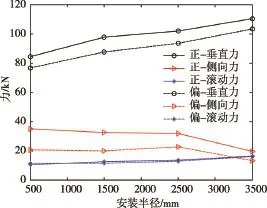
图6 正、偏楔形盘形滚刀所受平均载荷

图7 正、偏楔形盘形滚刀载荷相对减小量

从图6中可以看出正、偏楔形盘形滚刀所受的垂直力和滚动力总体上都是随着盘形滚刀安装半径的增大而增大。其中垂直力的增长幅度较大，滚动力的增长幅度较小。侧向力随着盘形滚刀安装半径的增大而减小。偏楔形盘形滚刀在不同安装半径下垂直力、侧向力和滚动力总体上都是比正楔形盘形滚刀所受的垂直力、侧向力和滚动力小。

从图6和图7中可知，正、偏楔形盘形滚刀垂直力之间的差值和载荷相对减小量都随着滚刀安装半径的增大而不断减小，载荷相对减小量减少较为平缓，在500mm安装半径处的相对减小量为10%，在3500mm安装半径处的相对减小量为7%。

随着盘形滚刀安装半径的增加，正、偏楔形盘形滚刀所受的侧向力的减小量和载荷相对减少量都在不断减小。在滚刀安装半径为500mm处，正、偏楔形盘形滚刀侧向力的减小量为13.206kN，相对减小量为38%，在滚刀安装半径为3500mm处，侧向力的减小量为6.415kN，相对减小量为30%。载荷相对减少量减少趋势较为明显。这是由于偏楔形盘形滚刀随着安装半径的减小，其刀刃内、外刃角相差较大，滚刀破岩时侧向滑移的减少量较多，破岩节能较大，侧向力的减少量较大。随着盘形滚刀安装半径的增加，偏楔形盘形滚刀的刀刃内、外刃角相差较小，其与正楔形盘形滚刀的刀刃结构差距较小，侧向力的减小量较小。

3.3 不同切深载荷对比分析根据滚刀仿真载荷时间历程曲线，计算出正、偏楔形盘形滚刀在安装半径为1500mm时破岩0～0.2s时间内不同切深条件下的平均载荷，见表7。

由表7可进一步算出偏楔形盘形滚刀在安装半径为1500mm时的不同切深条件下的垂直力、侧向力和滚动力较相同安装半径正楔形盘形滚刀减小量的百分比，见表8。

由表8可以看出，正、偏楔形盘形滚刀垂直力和侧向力的减小相对量随切深呈反方向变化，亦即，偏楔形盘形滚刀垂直力较正楔形盘形滚刀垂直力减小相对量随安装半径的增加而减小；而偏楔形盘形滚刀侧向力较正楔形盘形滚刀侧向力减小相对量随安装半径的增加而增加。以安装半径1500mm为例，垂直力在切深6mm的减小相对量为19.28%，在切深10mm为10.15%；而侧向力减少相对量在切深6mm为10.29%，在切深10mm为38.98%；

不同切深条件下的盘形滚刀所受的平均载荷可以显示出盘形滚刀在不同切深条件下的受载特点。正、偏楔形盘形滚刀在不同切深条件下的受载折线图如图8所示。

表7 滚刀不同切深时平均载荷

表8 不同切深、安装半径为1500mm的偏楔型盘形滚刀较相同安装半径的正楔形盘形滚刀破岩力减小百分比

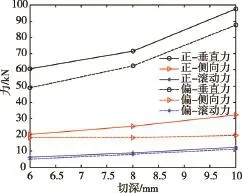
图8 不同切深下滚刀平均载荷

从图8可以看出：正、偏楔形盘形滚刀所受的垂向力、侧向力和滚动力都随着滚刀切深的增加而增加。其中正楔形盘形滚刀所受垂直力大于偏楔形盘形滚刀所受载荷，正、偏楔形盘形滚刀所受的侧向力的差值随着滚刀切深的增加而增大，这是由于滚刀切深较小时，滚刀刃圆弧与岩石接触破岩，滚刀刃侧面与岩石接触较少，随着切深增加，滚刀刃侧面与岩石接触面积增大，偏楔形盘形滚刀破岩优势体现出来；正、偏楔形盘形滚刀所受的滚动力基本上没有差别。

4 结论

（1）正、偏楔形盘形滚刀垂直力和侧向力的减小相对量随安装半径的增大而减小，以切深10mm为例，垂直力在500mm安装半径处的减小相对量为10%，在3500mm安装半径为7%；侧向力减少相对量在安装半径500mm处为38%，在安装半径3500mm处为30%；（2）正、偏楔形盘形滚刀垂直力和侧向力的减小相对量随切深呈反方向变化，以安装半径1500mm为例，垂直力在6mm切深的减小相对量为19.28%，在10mm切深为10.15%；侧向力减少相对量在切深6mm为10.29%，在切深10mm为38.98%；（3）正、偏楔形盘形滚刀滚动力的减小相对量随安装半径变化的随机性较垂直力和侧向力为强，以切深10mm为例，在500mm安装半径处，增加10.89%；而在1500mm安装半径，则减小8%；在2500mm和3500mm减小相对量分别为2.7%和4.03%。