基于灰色模型的中国天然气海上进口需求量预测

魏 帅 崔 巍 胡 轩 李 俊，2 杨海峰，2

（1.大连海事大学航运经济与管理学院，辽宁 大连 116026；2.重庆市电力公司发展策划部，重庆 400141）

0 引言

2017年是国家《大气污染防治行动计划》的目标年份，为解决北方地区严重的大气污染问题，多地煤改气进度超过规划［1］，其他工业用户对天然气的需求也在迅速增加，如发电和工业燃料用气在2017年年均大幅增长。目前，中国的能源现状是缺油少气［2］，国内四大主要气田塔里木、长庆、青海、川渝每年的产量都在增长，10年前这些气田的产量只有500 × 108m3／a［3］，而2017年已经接近1 000 × 108m3，年增幅超过7%，但这样的增幅与17%的需求增幅相比，仍有很大差距。过去3年，中国天然气平均消费总量接近2 000×108m3，平均进口量超过650×108m3，对外依存度高达35%。在国内天然气产量短期内难以大幅提升的情况下，天然气消费量骤增时，供应主要靠进口来补充，同时靠储气设施中的存量来满足［4］。天然气进口量从2010年不足20×108m3，到2017年超过900×108m3，年均增长率接近50%，这个增速使中国首次超过韩国成为全球第二大天然气进口国［5］。从全球范围而言，天然气进口渠道主要包括管道气进口和海上气进口［6］。由于中俄西线和东线预计均将于2020年及以后投产，在此之前陆上管道气进口量难以大幅增长，因此海上气进口增速将持续保持高位［7］。较为精确地预测近期海上天然气进口量不仅可以对现有液化天然气的进口能力进行评估，更好地了解供需和进口趋势，而且可以为近期新的沿海天然气接收站和储罐等基础设施建成投运提供决策支持，进一步提升中国的天然气进口能力和水平。

笔者研究的主要目的是建立一个与数据吻合较好的模型对中国海上天然气进口量进行预测。中国天然气产量和消费量的历史变化趋势可认为是受政策驱动、宏观经济形势和供需基础设施影响的综合结果［8-9］，2006-2017年中国天然气进口量的数据模式呈现明显的非线性增长特征。由于历史天然气需求的复杂性和影响需求因素的不确定性，灰色模型方法可认为是预测当前中国短期天然气进口急剧增长最合理的模型［10］。首先，笔者结合历史和近期相关数据，对构建出的3种灰色模型进行检验和适应性分析；其次，对中国海上天然气进口量进行了预测，并与国际相关能源机构报告和其他公开资料的结果进行了比较，验证了模型和结果的合理性；最后，总结预测结果，为中国天然气能源安全和海上进口战略提供有益的启示。

1 灰色预测

灰色建模方法最基本的形式是GM（1，1），并通过数据累加（AGO）、灰色模型、数据累减（IAGO）3个基本步骤实施。灰色预测最显著的特征是AGO，在此过程中对选定的数据模式进行预处理，以减少其不规则性，生成具有强规律性的序列，有诸多学者采用灰色建模方法预测能源问题［10-15］。

1.1 基本灰色模型GM（1，1）

步骤1：考虑具有n个项的非负时变序列X(0)，它代表中国海上天然气进口量。

步骤2：在式（1）上执行一次数据累加（1-AGO）；它变成了一个时变单调增长序列，如式（2）所示：

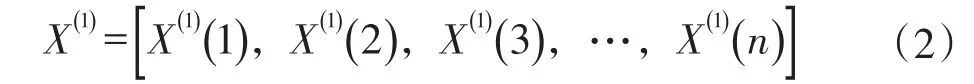
式中，

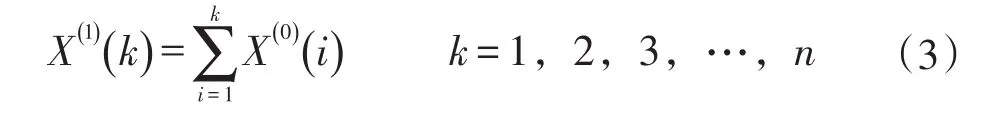
步骤3：定义GM（1，1）的灰色微分方程：

式中，X(0)(k)为灰导数；为灰导数的背景值，其中0＜p＜1，通常取p＝0.5；a、b分别为待辨识的参数，a为发展系数，b为灰作用量。

步骤4：GM（1，1）的白化微分方程可根据单调递增级数 X（1）构造如下：

步骤5：用最小二乘法求出的a、b值如下：

式中，

步骤6：设置初始值X(1)(1)＝X(0)(1)，时间响应方程如下：

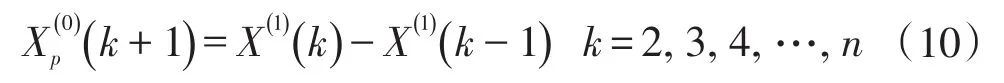
或

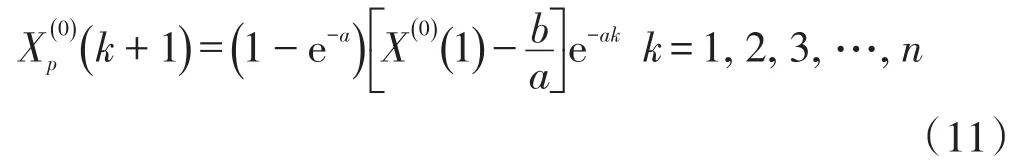
1.2 两次拟合GM（1，1）

求出GM（1，1）的参数a和b后，为提高精度，对其进行第二次拟合估计，将时间响应方程写为：

由于：

写成矩阵形式即为：

式（14）中，

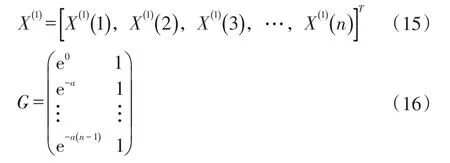
由最小二乘法，有：

1.3 灰色非线性Verhulst模型GVM（1，1）

GVM（1，1）的幂指数函数保证了非线性数据模式的特征，并增强了模型的拟合度［16］。GVM（1，1）的构造步骤1和2遵循GM（1，1）的相应步骤，其余步骤如下。

步骤3：GVM（1，1）的灰色微分方程定义为：

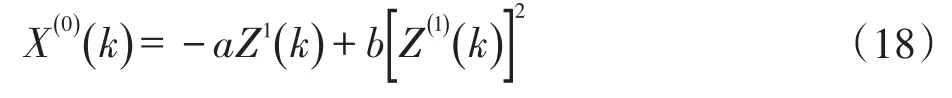
式中，X(0)(k)、Z1(k) ，a和b与GM（1，1）中所描述的相似。

步骤4：GVM（1，1）的白化微分方程可根据单调递增级数X(1)构造如下：

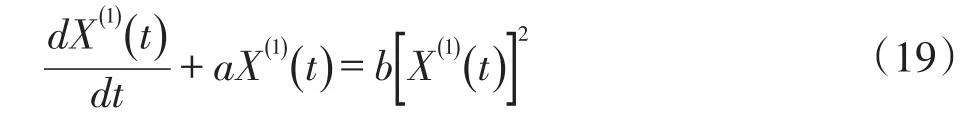
步骤5：用最小二乘法求出的a、b值如下：

式中，

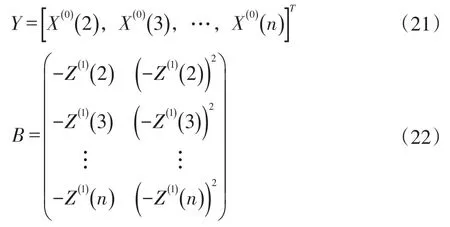
步骤6：设置初始值X(1)(1)＝X(0)(1)，时间响应方程如下：

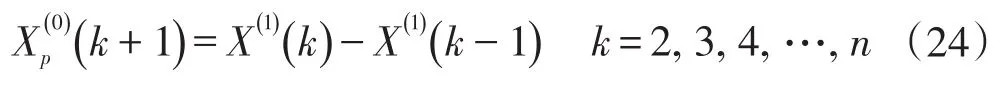
或

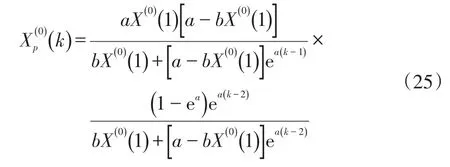
1.4 模型检验试验

模型建立后须使用相关检验方法检测模型稳健性和准确性是否达标，笔者拟用下面几种方法对模型进行检测［10，17］。

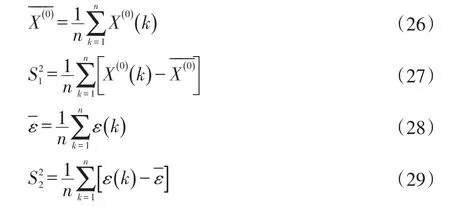
1）均方差比C检验：

式中，C也称噪声比，C值越小模型越精确。

2）小误差概率P检验：

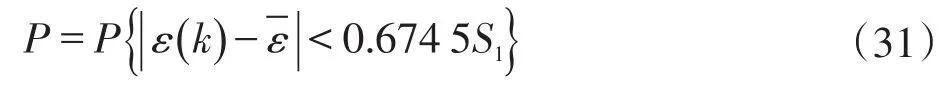
P值越大，吻合精度越高。

3）均方根误差（RMSE）、平均绝对百分比误差（MAPE）和平均绝对偏差（MAD）检验：

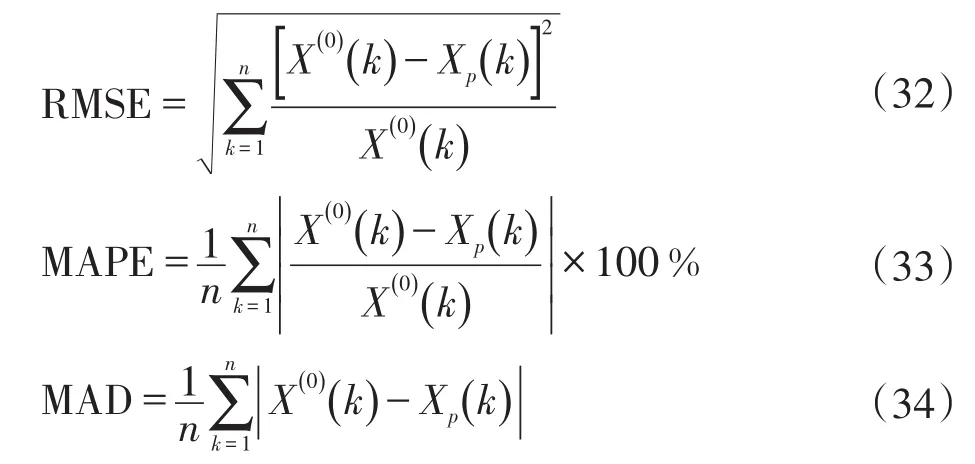
通常，RMSE、MAPE和MAD值越低，模型预测越精确。根据Lewis法则，MAPE值小于10%表明预测结果极好，在10%～30%表明预测结果优良，大于50%表明预测结果差。精度检验对照表如表1所示。

2 实证结果

2.1 数据来源

研究中用于构建预测模型的数据来源于2007-2018年《BP世界能源统计》、国家发展和改革委员会和公开资料整理。数据集分为建模数据集和测试数据集两部分，建模数据集为中国2006-2015年海上天然气进口量，测试数据集为中国2016-2017年海上天然气进口量。

表1 灰色模型精度检验对照表

2.2 模型参数和时间响应方程

利用Matlab R2012a软件计算得到相关数据，见表2。

表2 模型参数和时间响应方程表

2.3 模型适应性

GM（1，1）、两次拟合GM（1，1）和GVM（1，1）的建模和测试见图1和表3。数据结果显示，由于GVM（1，1）的指数型特征，在建模期拟合数据方面比GM（1，1）和两次拟合GM（1，1）表现得更好，而在测试期预测中国骤增的高度波动的海上天然气进口量时，GVM（1，1）明显不能作为合适的预测模型。因此，不再对GVM（1，1）作进一步分析。根据表1，在建模和测试期间，GM（1，1）和两次拟合GM（1，1）两种灰色模型的精度等级均达到Ⅰ级，可视为高度精确的预测。根据模型检验试验，从表3可以看出，GM（1，1）和两次拟合GM（1，1）的绝对百分比误差（APE）值在建模期前期较高，中后期较低，表明在中后期两个模型都能较好地预测进口需求。在测试期GM（1，1）和两次拟合GM（1，1）的APE值均保持在较低的水平，通过RMSE和MAPE值可知，两次拟合GM（1，1）的性能相对优于GM（1，1）。

2.4 海上天然气进口量短期预测

图1 GM（1，1）、两次拟合GM（1，1）和GVM（1，1）的适用性比较图

通过GM（1，1）和两次拟合GM（1，1）对中国海上天然气2018-2020年进口量进行预测，并与相关研究报告在特定年份预测的数据进行比较。海上天然气进口量短期预测见图2，从图2可以看出，这两种模型的预测结果基本一致，即到2019年底中国海上天然气进口量将有望突破700×108m3，2020年底将超过840×108m3，海上天然气进口量将以年均21%的速度增长。GM（1，1）和两次拟合GM（1，1）在2017年的预测结果与2015年EIA国际天然气进口预测数据近似相等，对2020年的预测结果与图2图例列出的研究报告对2020年的预测结论非常接近。

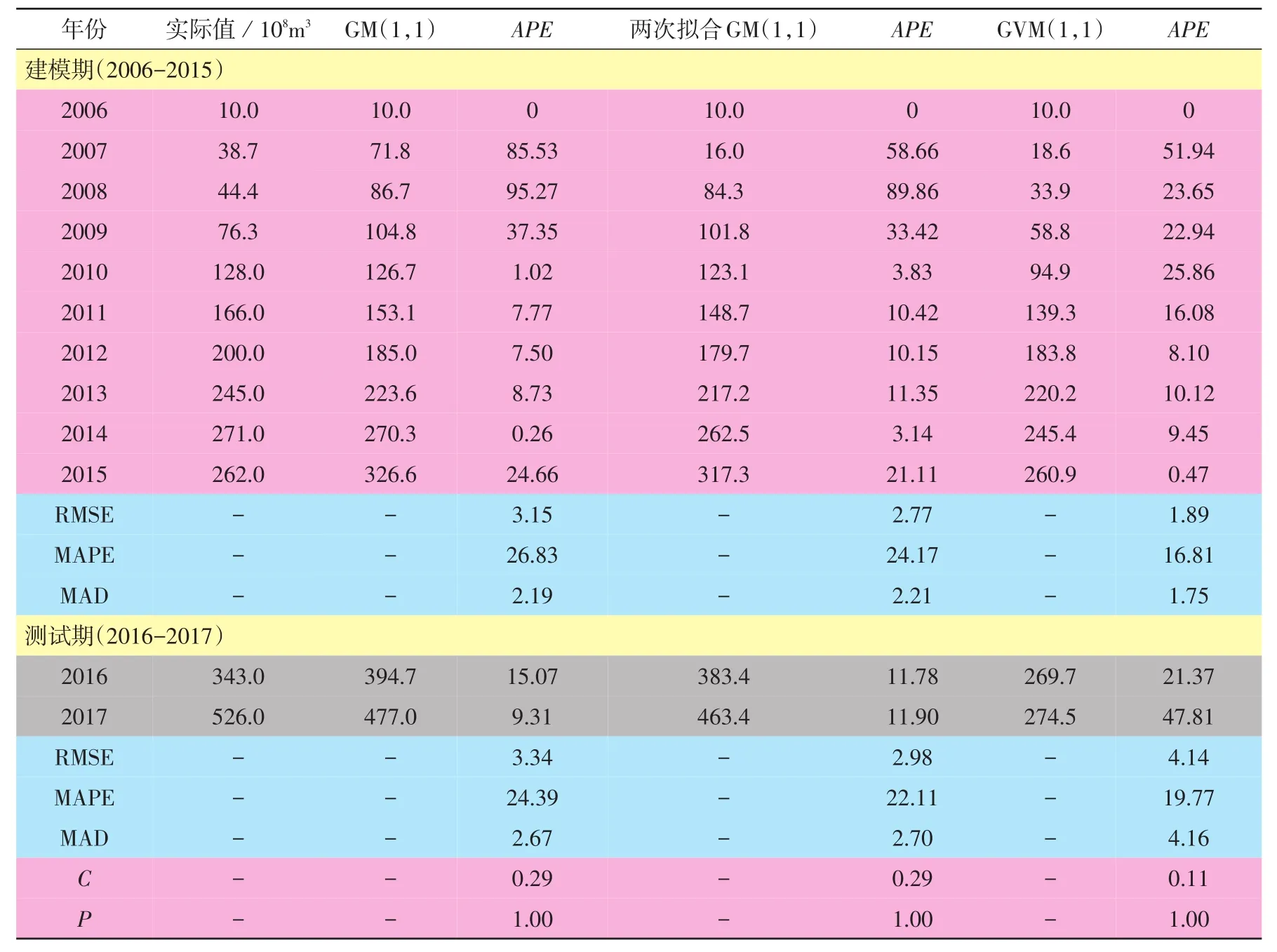
表3 GM（1，1）、两次拟合GM（1，1）和GVM（1，1）的适用性比较表

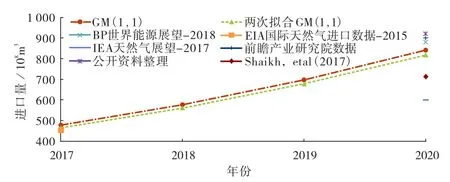
图2 海上天然气进口量短期预测图

3 结束语

笔者研究的目的是建立合适的灰色模型预测中国海上天然气进口量。根据试验比对和预测结果，GM（1，1）和两次拟合GM（1，1）能很好地适应中国海上天然气进口的非线性增长模式，在统计上属于较高精度预测。该模型表明，中国海上天然气进口需求量到2020年将超过840×108m3。在当前中国能源消费清洁化转型的大趋势下，随着中国煤改气政策的进一步落实，燃气发电和交通运输用气需求量增长，进口天然气成为重要的供应保障手段，因此中国海上天然气进口需求量将持续增加，2020年前中国海上天然气接收站周转率将保持高位。随着天然气资源对外依存度的迅速增长，人们将越来越关注中国天然气的供应保障安全，应采取确保海外天然气稳定供应、实现进口渠道多元化和加快推进储气设施建设等手段保障供给。由于近期中国在页岩气领域取得的重大突破，天然气进口量增速或将放缓，有效保障天然气安全供应。