基于模糊贝叶斯网络的洞室事故人因分析

，

(1.三峡大学 水利与环境学院，湖北宜昌443002；2.西藏开发投资集团有限公司，西藏拉萨850000)

随着国民经济的发展，中国的水利工程得到了很好的建设，水利工程在建成之后相继投入生产使用，水利工程的建设是一个投资大、周期长、工作环境复杂的项目。近年来，中国建筑施工事故时有发生，安全管理任务愈加显得重要。造成事故发生的因素众多，人为因素导致的事故高达90%[1]，有必要采取措施减少人为因素所导致的事故发生。面对水利工程高危施工作业，大部分研究把安全防范措施方面作为主要研究对象，对施工安全风险量化的研究相对较少。贝叶斯网络是一种基于网络推理风险量化的方法，但是其需要用先验概率分布进行推理。目前，很多贝叶斯网络中基本事件的发生概率采用确定值进行分析，如郑霞忠等[2]利用贝叶斯网络对边坡开挖进行概率评估，周忠宝等[3]结合贝叶斯网络及故障树对核电站进行可靠性分析，陈兆波等[4]利用贝叶斯网络对煤矿事故原因进行人因因素推理，王俊人[5]利用贝叶斯网络对地铁工程进行风险分析，毛宇辰[6]对地下厂房开挖进行动态预测，及文献[7]采用贝叶斯网络及人为因素分析和分类系统框架(HFACS)分析航空事故。由于水利工程施工系统的组织、监督、安全行为具有不确定性以及事故样本少，可利用的历史数据有限，难以将精确概率赋值给基本事件。因此，本文针对水利工程高危施工作业，从人因角度出发，利用修改后的人因框架体系(HFACS)辨识并构建事故树，利用模糊集理论对贝叶斯网络进行模糊，建立模糊贝叶斯网络，旨在量化及处理水利工程施工安全事故的模糊信息，同时为施工安全提供有效预防措施。

1 人为因素的辨识

人为因素分析与分类系统 ( human factors analysis and classification system，HFACS) 是基于系统理论的人因事故模型和事故分析工具[8]，HFACS对4个层次企业组织影响、安全监督、不安全行为的前提条件和施工人员的不安全行为进行了明确的划分，可以找出导致事故发生的主要人为因素，但是HFACS框架不是一成不变的，为更好适用水利工程施工高危行业，本次利用修改后的HFACS框架[9]，并结合长江干流3项大型水利工程建设过程中发生的15起水利工程洞室坍塌事故，通过专家打分法辨识导致事故发生的主要人为因素，并建立洞室坍塌事故树(图1)，代码含义见表1。

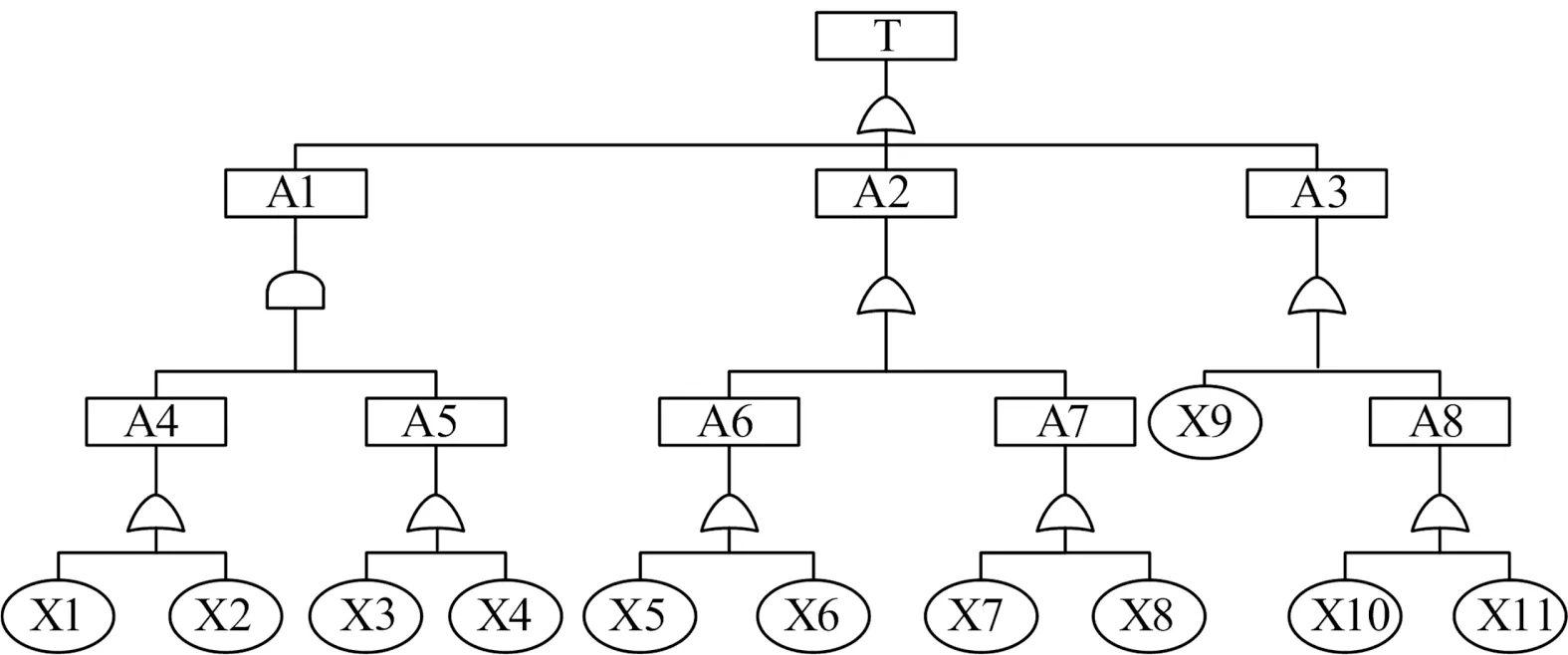
图1 洞室坍塌事故树

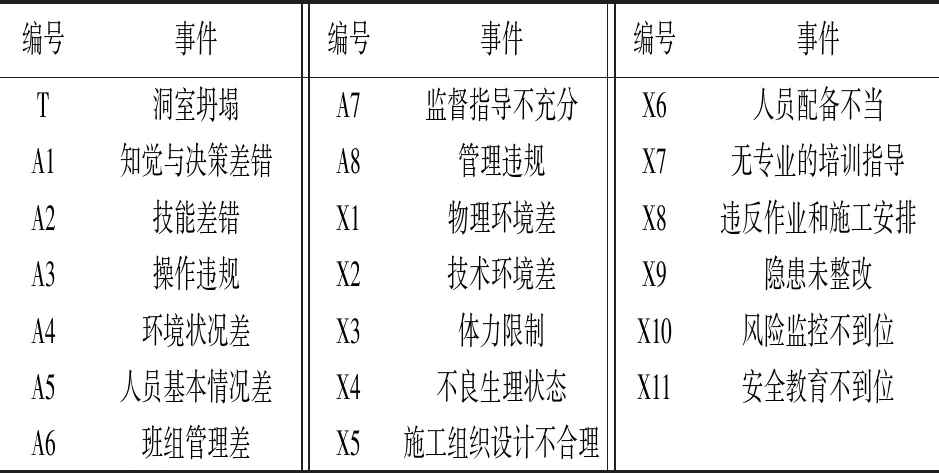
编号事件编号事件编号事件T洞室坍塌A7监督指导不充分X6人员配备不当A1知觉与决策差错A8管理违规X7无专业的培训指导A2技能差错X1物理环境差X8违反作业和施工安排A3操作违规X2技术环境差X9隐患未整改A4环境状况差X3体力限制X10风险监控不到位A5人员基本情况差X4不良生理状态X11安全教育不到位A6班组管理差X5施工组织设计不合理

事故树模型具有很好地逻辑结构关系，但是条件概率的确定只有2种：0或1，其值太过绝对化，往往不符合实际情况，贝叶斯网络却具有良好表达不确定关系以及双向推导能力[10]。为此，本次利用事故树转化为贝叶斯网络结构，转化方法如下[11]：①对事故树每个事件在贝叶斯网络中建立一个节点，并以事件名称命名；②节点间有向弧表示事故树中事件间的逻辑结构关系，建立拓扑结构；③根据事故树各事件发生概率确定父节点先验概率及子节点条件概率。

2 模糊贝叶斯网络的概率分析

2.1 先验概率的确定

2.1.1模糊数及运算[12]

模糊集是指用于表示界限或边界不分明的具有特定性质事物的集合，其基本思想是把经典集合中的绝对隶属关系灵活化，隶属度不再局限于取0和1，而是可以取0～1之间的任一数值。目前，比较常用的是三角模糊数和梯形模糊数。

模糊数是模糊集理论中的一个基本概念，对于不确定的信息，如“很高”“一般”等模糊性语言，模糊数可以进行良好的处理。一般地，对于三角模糊数A(a，b，c)，其隶属度函数为：

(1)

对于梯形模糊数A(a，b，c，d)，隶属函数表示为：

(2)

本文选取梯形模糊函数及三角模糊函数，其可进行加、减、乘、除等运算[13]。

2.1.2专家语言模糊化处理

采用此方法可以在难以给出精确值的状态下，通过引入专家语言变量可以对评价对象给出更加直观的表达。Wickens[14]把事件发生概率分为：非常高(VH)、高(H)、偏高(FH)、中等(M)、偏低(FL)、低(L)、非常低(VL)7个语义值，其形式[5]见表2。

表2 模糊数λ和λ-截集

为了得到更加精确的事故发生概率，采用m个专家进行评判得到综合评判结果，具体公式如下：

(3)

式中Pi——第i个事件发生的模糊概率；Aim——对第i事件第m个专家评判的模糊值；n——事件数目。

2.1.3模糊数的求解

为了把各事件发生的模糊可能值转化为精确值，需要进行解模糊，Liou提出积分值法[15]，此方法可以利用λ-截集的运算对模糊数处理，其方法计算简单且容易理解，本文采用此方法，计算公式如下：

I=αμR(A)+(1-α)μL(A)

(4)

式中I——模糊数的代表值；α∈[0,1]，代表乐观系数，α=0、1时，分别对应解模糊数A得到的模糊化值的上、下界，α=0.5时，为模糊数A解模糊化值的代表值；μR(A)、ML(A)——模糊数左、右隶属函数反函数的积分值，μR(A)及ML(A)用λ-截集表示为：

(5)

(6)

式中mλ、nλ——模糊数A的λ-截集的上、下界，λ=0，0.1，0.2，…，1；△λ=0.1。

2.2 条件概率的确定

对于条件概率的确定，文献[16]把节点分为2类:对于节点间明确存在逻辑关系的，即“或”“与”，条件概率可直接通过逻辑关系分析得出；对于由节点间相互作用或共同作用导致事故的发生，由专家经验或通过数据学习得到节点的条件概率。由于大量水利工程事故数据难以获取，条件概率的确定大多采用专家经验给出，对于父节点多的情况下，由专家经验给出节点的条件概率难免会出现模糊不清的状态。鉴于此，本文采用单个因素对子节点的作用，然后进行加权综合来确定条件概率，计算公式为[17,20]：

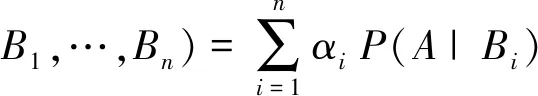
(7)

式中：αi为影响事件A的父节点各因素两两比较得到的权重。求权重αi的方法本次采用AHP。对于P(A|Bi)求取，采用专家调研的方法给出，为方便专家表述，采用联合国政府间气候变化专门委员会(IPCC)提出的7 级风险发生概率表述方式[18-19],见表3。

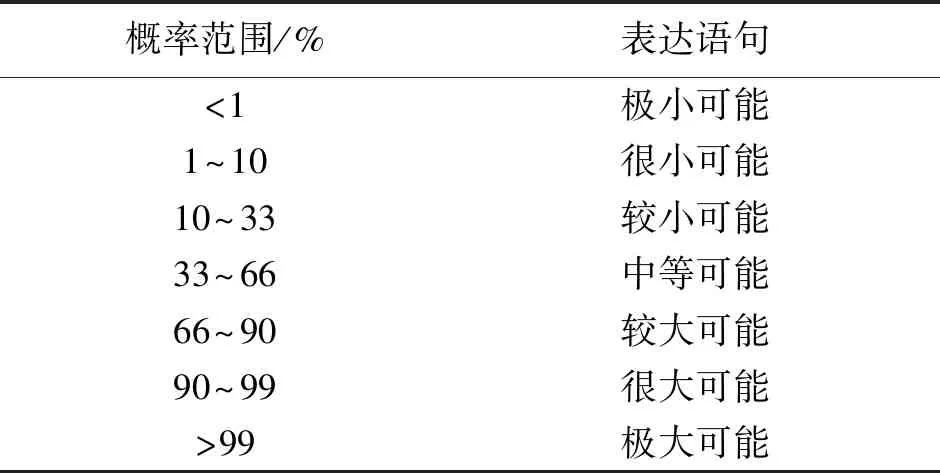
表3 IPCC 的概率定性描述

3 工程实例分析

3.1 模糊贝叶斯网络的构建

本次针对15个水利工程洞室坍塌事故，基于专家建立的事故树为前提，根据第1节事故树向贝叶斯网络转化规则得到贝叶斯网络结构(图2)，进行安全风险分析。

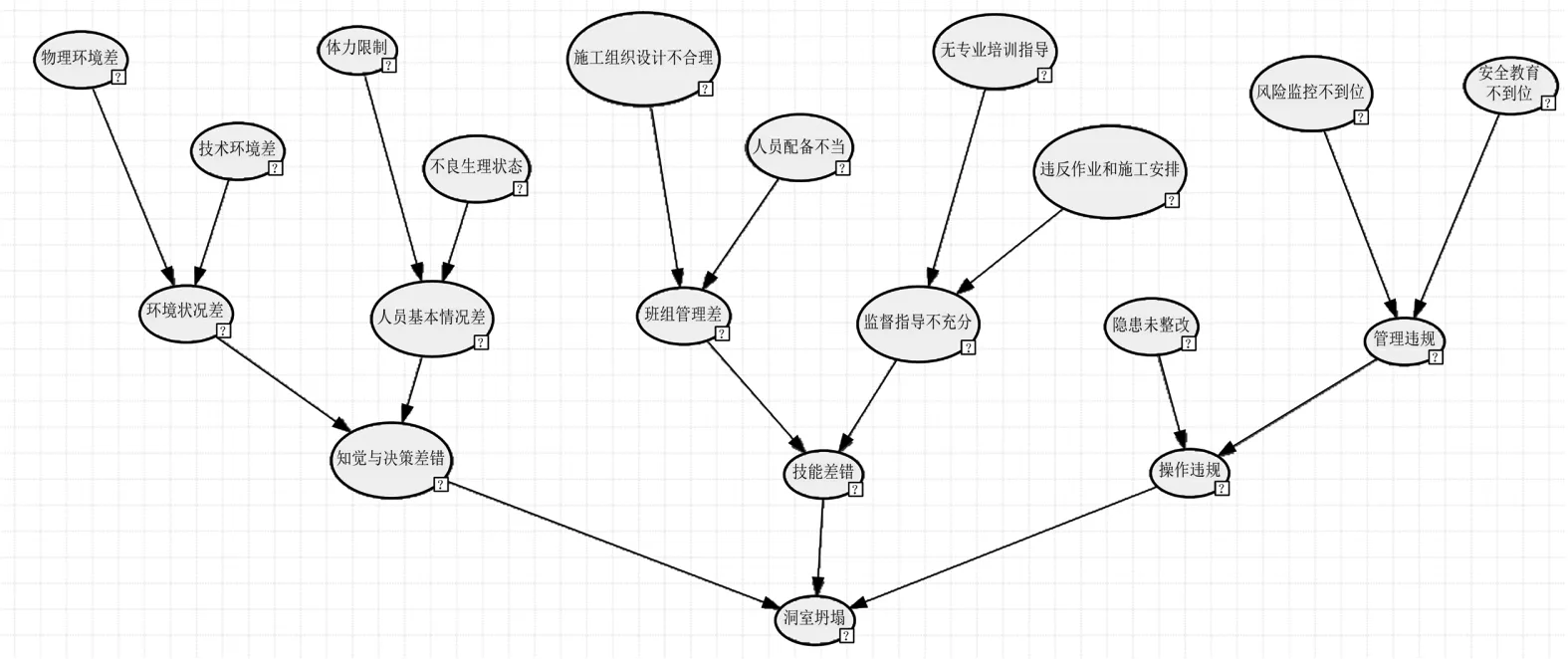
图2 洞室坍塌贝叶斯网络

根据前面介绍，这里以X11为例介绍先验概率的确定。请5位生产安全专家对事件分别给出模糊概率值的语言描述，采用算数平均法得到综合的模糊概率值。根据公式可知，X11的平均模糊数为：

0.4)+(0.1λ+0.2)+(0.1λ+0.4)，(-0.1λ+

0.6)+(-0.1λ+0.5)+(-0.1λ+0.6)+

(-0.1λ+0.5)+(-0.1λ+0.6)]=[0.1λ+

0.32,-0.1λ+0.56]

同理可得到其他基本事件发生模糊数。这里求出先验概率发生即α=0.5时的代表值。根据公式可得节点X11先验概率为P(X1=0)=0.44,P(X1=1)=0.56，同理可得其他节点概率。

对于条件概率的确定，以节点“环境状况差”为例，进行条件概率的确定，其概率计算公式为：

P(A4│X1,X2)=(α1P(A4│X1)+

α2P(A4│X2)

根据5位专家对“物理环境”“技术环境”的两两比较，得到α1=0.36，α2=0.64。得到子节点“环境状况差”在单个父节点影响下的条件概率见表4。

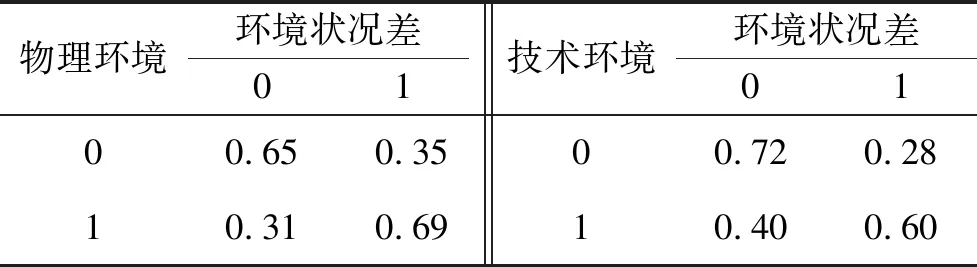
表4 节点X1、X2单个影响下节点A4的条件概率

在物理环境差、技术环境差的状态下，节点环境状况差的条件概率为：

P(A4=0│X1=0,X2=0)=0.6948

同理，可以得到各种状态下“环境状况差”的条件概率见表5。

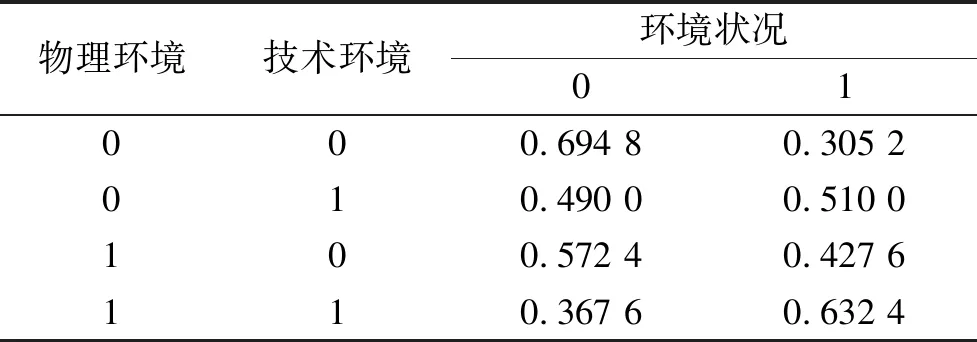
表5 节点X1、X2综合影响节点A4的条件概率

以此类推，得出其他节点条件概率值。

3.2 洞室坍塌事故的人因推理

在给定贝叶斯网络结构及参数确定的条件下，需要对贝叶斯网络进行推理分析，其推理过程意味着在给定1组证据变量(原因) 的情况下，计算1组查询变量(结果)的概率分布，可以进行安全风险预测。本研究采用GeNIe软件进行贝叶斯网络的推理，将经过分析后的数据进行整理输入到软件中(图3)。

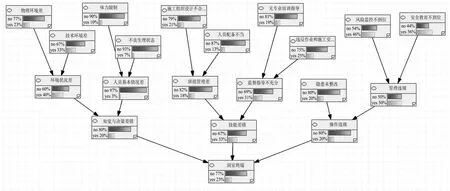
图3 洞室坍塌的贝叶斯网络

从图中看出目标事件发生的概率为23%，不发生的概率为77%。另外，当后果事件发生时，可以计算出其他事件的后验概率，当T=1时，X2、X11、X10概率较大，即后果事件发生，很可能由于技术环境差、安全教育不到位及风险监控不到位引起。

3.3 敏感性分析

敏感性分析可以确定对于事件发生贡献最大的因素，通过控制基本事件的发生，进而降低顶事件发生的概率，保障施工的连续性以及人身财产安全，所以对贝叶斯网络进行敏感性分析是有必要的[21]。设敏感性因子(sensitivity index)为α，则第i个基本事件的敏感性因子为：

(6)

式中，γi为后果事件发生概率与第i个基本事件不发生时后果事件发生概率的差值与γi为后果事件发生概率的比值；γmax=max{γi}。利用GeNIe软件及式(6)，可计算出基本事件的敏感性因子，见表6。

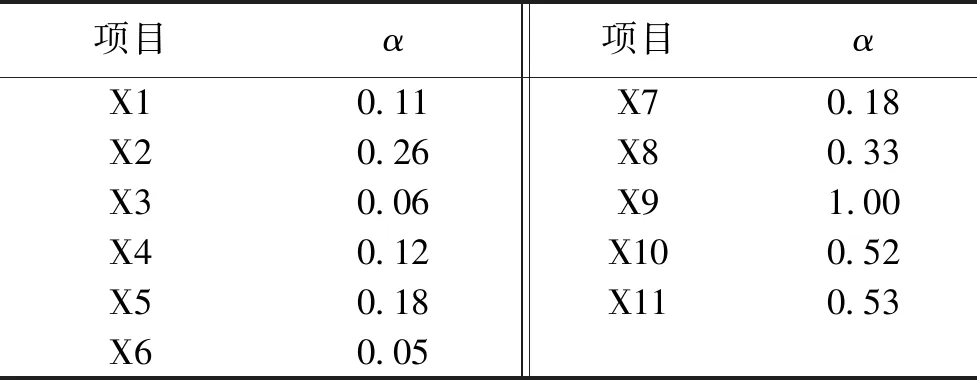
表6 基本事件的模糊敏感性因子

从表中可以看出α1、α2、α3、α3、α4、α5、α6、α7、α8、α9、α10、α11结果分别为0.11、0.26、0.06、0.12、0.18、0.05、0.18、0.33、1.00、0.52、0.53，故基本事件影响因子排序为：α9>α11>α10>α8>α2>α7>α5>α4>α1>α3>α6。这说明隐患未整改是最不利因素，因此应该更加重视隐患的排查。安全教育不到位，风险监控不到位，违反作业和施工安排及技术环境差在事故人为因素中占有很大比重，因此在施工中应进行安全教育，提高自身的安全意识和自我保护能力，此结论与事故报告中结论一致，说明此方法具有一定的适用性。

4 结论

a) 考虑到水利工程的特点并针对高危施工作业，本文利用修订后的HFACS框架，并结合洞室坍塌事故分析报告辨识主要人为因素，最后基于事故树及模糊集理论建立符合水利工程特点的模糊贝叶斯网络。

b) 模糊贝叶斯网络的结果分析表明，当洞室坍塌时，最可能原因为安全教育、风险监控不到位，技术环境差。敏感性分析找出：洞室坍塌中隐患未整改，安全教育不到位，风险监控、违反作业和施工安排，是关键事件，这与前面得出的后验概率大者基本一致，并且此次预防措施与事故报告基本一致，说明此方法的可行性以及适用性。

c) 本文利用模糊贝叶斯网络对水利工程事故进行分析，其优点对于不确定性表达能够量化并能清晰地得出主导因素，且结果基本与实际情况一致。此方法不仅适用于水利工程高危施工作业，同时，为其他领域提供借鉴作用。