微起伏地面的建筑物后向散射特性研究

郑军生，杨 菲，张 海，曾 超

(中国工程物理研究院 电子工程研究所，四川 绵阳 621900)

0 引言

城市目标遥感问题越来越受到关注，城市区域的遥感可用于人口的估计、经济规划以及建设规划[1-3]。城市目标的遥感通常使用测量的方式获得[4]，这种方式耗费很多时间，也需要很多财力支撑。城市目标遥感还可用于救灾，对受灾区域的灾害评估[5-7]。对于城市遥感问题，合成孔径雷达(SAR)是一个很好的工具，它可以提供城市区域的高分辨、覆盖范围广的雷达散射图像。

城市目标遥感数据解译的基础是建筑物散射特性，研究雷达回波和建筑物的几何特性、介电特性的关系。如果没有一个好的物理模型，就无法对遥感数据进行深层次的解译。Franceschetti等[8]把建筑物简化为平行六面体，并研究了简化模型下的建筑物散射和电磁波的入射角、建筑物的方位角等的关系。文中将建筑物散射分为一次散射、二次散射和三次散射，并用几何光学法(GO)、物理光学法(PO)相结合的方法解析推导了简化建筑物的散射结果。简化建筑物的散射模型被用于建筑物SAR成像模拟和建筑物参数反演等[9-13]。然而，对像城市建筑物周围主要是水泥地或沥青地面，地面的参数不满足几何光学法、物理光学法的使用条件。针对这种情况，本文提出对地面一次散射用微扰法[14-16](SPA)计算，建筑物和地面的二次散射用GO-SPA计算，最后对计算结果做数值仿真分析。

1 理论模型

根据文献[8]的建筑物模型，将建筑物简化为平行六面体，建筑物放至在一个随机粗糙面描述的地面上，随机粗糙面用相关长度lc和均方根高度σ描述，如图1所示。

图1 建筑物和粗糙面的几何模型

建筑物散射分为墙面的一次散射、地面的一次散射、屋顶的一次散射、墙面—地面的二次散射和墙面—地面—墙面的三次散射，地面根据不同的粗糙度选择GO或PO。使用GO或PO方法，粗糙面需满足如下条件：

klc>6，lc2>2. 76σλ，

(1)

(2)

1. 1 地面一次散射

由Huygens原理，将入射场Ei、散射场Es以及粗糙面上的E(r′)均用粗糙面高度起伏kξ为微小量进行泰勒级数展开。散射场零阶解即是平面反射场，散射场的一阶解得到非相干散射场的散射系数。根据文献[15]Ulaby关于SPA的推导可得如下单位照射面积的非相干散射截面为：

σpq=16πk4cos4θ|apq|2S(2ksinθ，0)，

(3)

式中，p，q=H，V表示不同的极化状态，极化系数为：

aHH=R⊥，

aHV=aVH=0。

S为粗糙面高度起伏自相关函数的二维傅里叶变换，如果相关函数满足Gauss分布且随机粗糙面各向同性，则

(4)

1. 2 二次散射

将二次散射由相干部分σc和非相干散射部分σi构成，总的散射场表达式为：

σtotal=σc+σi。

(5)

将建筑物的墙面等效为光滑平面，经过墙面—地面散射的电磁波只有在特定的散射角度下才能被接收器接收到，相反，经过地面—墙面散射的电磁波需要经过相同的散射路径，所以接收到的回波强度是只计算墙面—地面散射的2倍，回波功率是只计算墙面—地面散射的4倍。相干散射部分可以等效为表面光滑的二面角散射，相干散射的散射截面为：

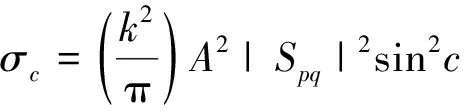
(6)

式中，Spq的定义参考文献[8]；A为经过墙面反射之后照射在地面的有效面积

A=hltanθcosФ。

(7)

根据1. 1节，非相干散射结果如下：

σi=4×16πAk4|Rpq|2cos4θS(kx+ksinθ，ky)，

RHH=R⊥(ψ)aHH(2Ф)，

RHV=R⊥(ψ)aHV(2Ф)，

RVH=R∥(ψ)aVH(2Ф)，

RVV=R∥(ψ)aVV(2Ф)。

式中，ψ为入射波对墙面的入射角；

y=arccos(sinθcosФ)；

aHH，aVV，aHV，aVH参考文献[15]Ulaby关于微粗糙表面散射的推导，

kx=-ksinθcos(2Ф)，

ky=-ksinθsin(2Ф)，

根据文献[8]，三次散射相较于一次散射、二次散射可以忽略。

2 数值仿真与分析

假设入射波频率为5 GHz，墙面材料的介电常数为4+0. 1j，地面的介电常数为7+0. 3j，建筑物的高为20 m，长为20 m。将简化的建筑物模型放置在均方根高度σ=0. 003 m，相关长度lc=0. 02 m的随机粗糙面上。

地面一次散射的RCS随入设角变化情况如图2所示，入射波的有效照射面积是400 m2。同极化HH和VV的RCS并不相同，从图中也可以看出，HH通道回波随着入射角的增大衰减的速度更快。交叉极化通道的回波为0。

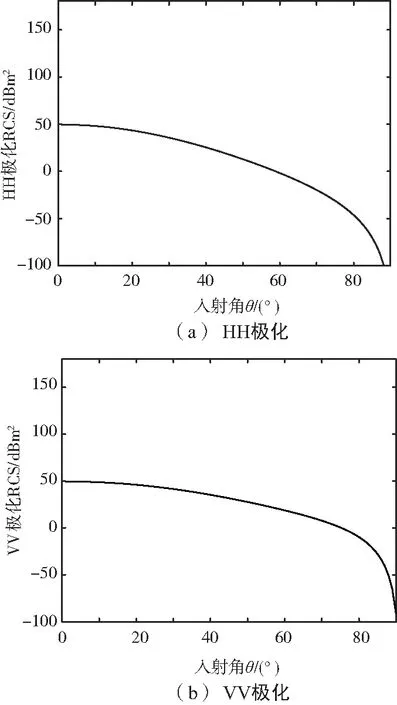
图2 地面一次散射RCS随入射角的变化情况

不同极化的二次散射RCS随入射角度变化情况如图3所示。对于同极化通道，在建筑物方位向Ф=0时有很强的相干回波，而交叉极化通道在Ф=0时RCS等于零。同极化RCS随着建筑物方位角变大而减小，交叉极化RCS随着建筑物方位角的增大而增大，当建筑物方位角大于一定角度之后，二次散射会完全湮没在一次散射中。HH极化和HV极化在很大入射角范围内RCS变化不大，VV极化呈现2个明显的波谷，分别对应于墙面和地面的布鲁斯特角。

通过比较图2和图3可以看出，二次散射在很大入射角范围内都是主要散射。

建筑物的二次散射强度受建筑物方位角的影响较大，如图4所示，当方位角小于8°时，RCS随着方位角的增大而急速减小，当方位角大于8°之后，随着方位角的增大RCS变化并不明显。

当建筑物墙面的介电常数或地面的介电常数在小范围内变化时，对二次散射的RCS影响并不明显，只有当介电常数变化较大时，RCS才会有明显变化，但RCS的趋势不变，只是回波功率的变化。

地面粗糙度对RCS的影响较大，如图5所示，所以对建筑物散射理论计算需要对地面进行精确建模，利用理论模型进行建筑物参数的反演首先要需要对地面的粗糙度进行精确估计。

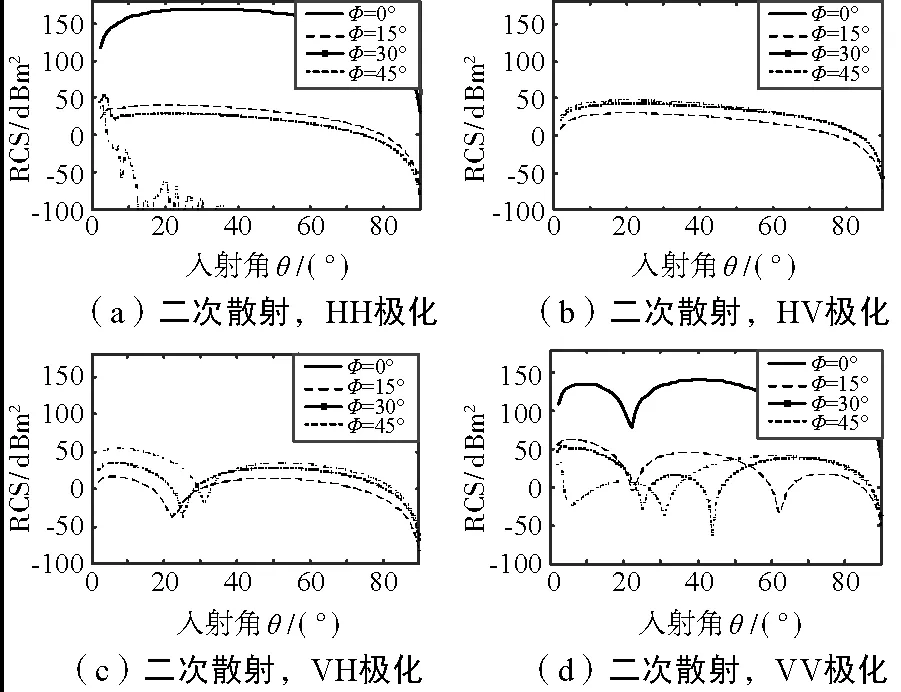
图3 二次散射在不同极化下RCS随入射角的变化情况

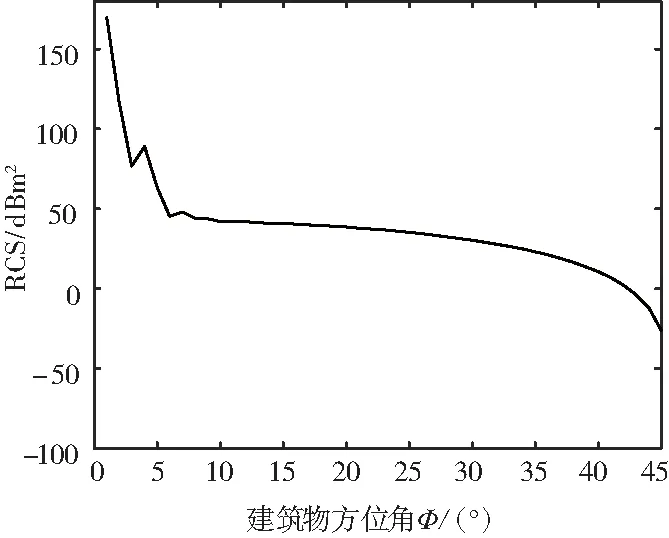
图4 二次散射和建筑物方位角的关系(入射角23°)

图5 均方根高度对散射的影响(建筑物方位角23°)

3 结束语

本文研究了当地面的粗糙度不满足基尔霍夫近似时，利用微扰法计算地面散射情况，并利用几何光学法和微扰法相结合的方法计算了建筑物和地面的多次散射情况，研究了建筑物RCS随着入射角、方位角和地面粗糙度的变化情况。当包围建筑物的地面的粗糙度较小时，建筑物是以二次散射为主，建筑物RCS和方位角有强相关性，当方位角较小时，回波较强，因为回波具有强相干性，当方位角大于42°时，二次散射几乎湮没在一次散射中。VV极化呈现2个波谷，分别对应建筑物墙面和地面的布鲁斯特角，如果能获得大角度范围VV极化的回波，可以通过这种特性反演墙面和地面的介电常数。由于一次散射交叉极化回波为0，可以利用此特性，利用交叉通道回波检测建筑物。地面的粗糙度对建筑物回波有较大影响，要利用建筑物散射理论模型反演建筑物参数，需要对地面粗糙度相关参数进行精确估计。