空间环境参数预报数据在轨控策略中的融合应用

刘 芳，蔡立锋，孙先伟，石 宁，苏 鹏

(航天器在轨故障诊断与维修重点实验室，陕西 西安 710043)

0 引言

随着我国卫星在轨应用技术的日益提高，为保证卫星成像要求和其他应用要求，轨道控制成为低轨卫星日常管理的一项重要工作。精细化管理的发展不仅对轨道控制效率和精度提出了更高的要求，也对控制效果的评估提出了更高的要求，尤其是低轨卫星轨道衰减快，轨道维持频率高，轨迹网保持成为低轨卫星生命周期中一项长期工作[1]。目前，已经有很多专家学者针对低轨卫星轨迹网保持方法开展了大量研究，文献[2]针对空间环境对超低轨道航天器轨道衰减影响进行了分析，但工程实践中针对空间环境突然变化引起的轨控效果变化及应对方法仍未有效解决。本文结合低轨卫星轨道维持方法及策略，采用空间环境预报参数对控后轨道变化反演结果进行策略制定，解决了控后轨迹网保持精度问题。按照卫星观测应用的要求不同又分为按轨迹网边界保持、按时间保持以及按兼顾轨迹网和时间二者进行保持3种方式[3]，结合某型卫星轨迹网边界保持过程，按照轨迹网边界(-L/2～L/2 km)兼顾保持时间为1个月以上的保持要求，在轨控策略的制定过程中，根据轨控策略进行轨迹网预报的计算，以验证轨控策略是否能够达到轨控要求，依据轨迹网预报情况对轨控策略进行修正和确定，周期变率的选择对轨迹网保持预报起着关键作用。利用求解经验公式的方法，给出了太阳活动、地磁活动与轨道周期变率之间的经验公式，由空间环境预报的变化推演出轨道周期变率的变化情况，解决了轨迹网预报不准确导致的轨控时间达不到要求或超出保持边界的问题，同时也为轨控参数的确定提供了有效参考和依据。

1 空间环境参数变化规律与趋势分析

图1 2014年太阳F10. 7数值变化情况

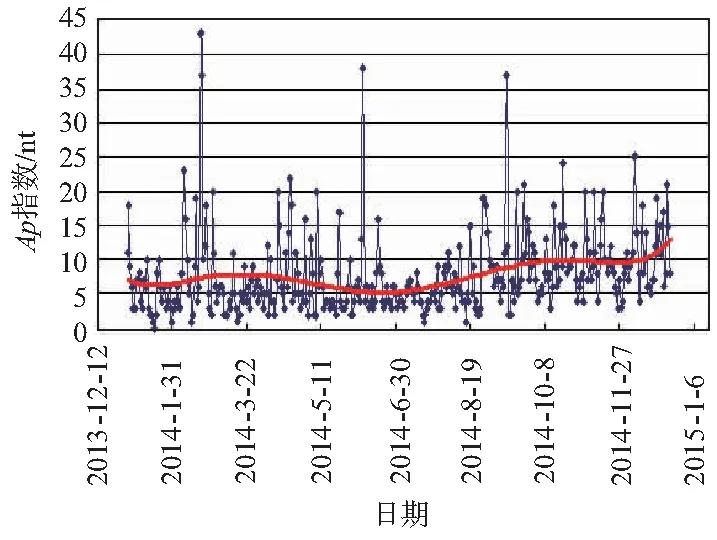
图2 2014年地磁指数Ap数值变化情况

由图1和图2可以看出，2014年太阳F10. 7流量的变化，未出现突然的跳变，平均值在150左右，而且很好地遵循了大气密度的半年周期变化[8]，即在4月、10月达到极大值，在1月和7月达到极小值。2014年地磁Ap指数的变化，极大值出现在2月、6月和9月，平均值在10左右，没有发生较大的磁暴，对空间环境影响不大。轨道周期变率变化趋势如图3所示，对比图1和图3可以看出，空间环境参数太阳F10. 7与轨道衰减的变化相关，即太阳F10. 7值越大，空间环境越差，轨道衰减越快，周期变率绝对值越大。

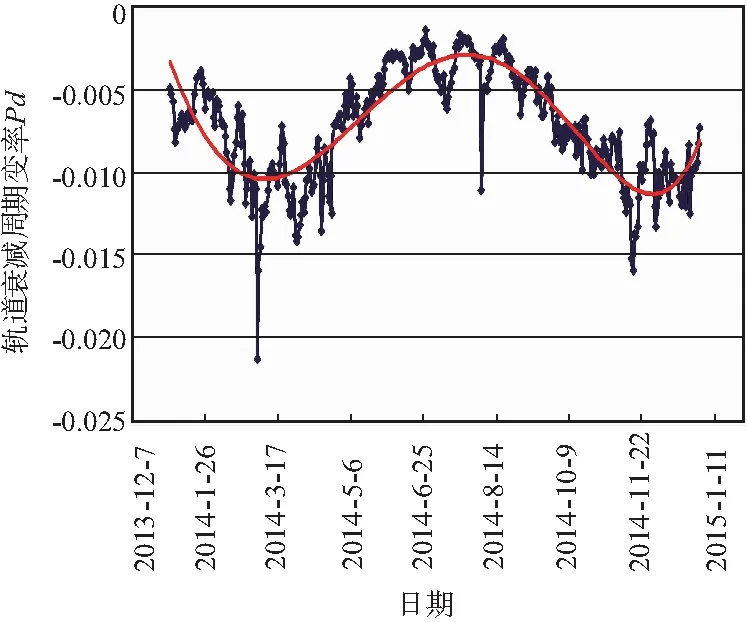
图3 2014年轨道周期变率变化情况

2 空间环境参数数据与轨控效果融合分析

2. 1 卫星轨道控制效果分析

2014年某型卫星轨道衰减如图4所示，全年共进行了8次轨道维持，其中，第3次轨道控制未达到时间保持要求。这次控制过后，由于空间环境突然变差，轨道衰减过快，未满足在时间上保持1个月以上的要求。按照控制要求进行轨道控制策略计算时，由于空间环境对轨迹网保持预报有一定影响，预报软件考虑了这个因素，将轨道周期变率作为一项计算参数进行考虑[9]。目前采用的周期变率是对轨控前一段时间的轨道衰减变化趋势分析得到的，如果轨控过后空间环境发生变化，引起周期变率变化较大，就很难准确地预报卫星轨迹网的变化。

以某次控制为例，在控制高度同样为70 m的情况下，根据预估的不同周期变率(Pd值)，对控制效果进行预估，Pd为-0. 002，-0. 002 5，-0. 003时的轨迹网预报情况如图5所示。当周期变率Pd=-0. 002 5时进行控制，轨迹网预报符合轨控要求，如果空间环境变好，周期变率绝对值变小；Pd=-0. 002，轨道衰减变慢，到达标称轨道时已经超出轨迹网西边界，不满足轨迹网保持要求；如果空间环境变坏，周期变率绝对值变大，Pd=-0. 003，轨道衰减加快就会提前到达标称轨道，导致很快飘回轨迹网东边界[10]，轨迹网保持时间不满足要求，造成频繁控制。

图4 轨道半长轴数值变化情况

2. 2 轨道周期变率与空间环境参数关系分析

提取2014年7月25日—8月19日的空间环境参数与轨道周期变率数据进行分析，如图6所示。可以看出，太阳F10. 7的数值不断增大，正好在8月1日达到了一段时间的峰值，对空间环境产生影响，造成卫星轨道衰减较快，轨道周期变率绝对值明显增大；地磁指数Ap变化比较平稳，均值在10左右，没有超过20，对空间环境影响不大。轨道周期变率与太阳F10. 7变化趋势基本一致，空间环境对轨道周期变率的影响有滞后现象[11]。

图6 轨道周期变率与空间环境参数关系

利用轨控后预报的周期变率对轨迹网进行预报，能够更加准确地对控后轨道变化情况进行有效分析，提高轨控的精细化管理程度，问题的关键在于目前的预报水平能否真实反应空间环境变化情况，下面会做进一步分析。

2. 3 空间环境参数实测值与预报值相关性分析

为了真实有效地反应数据的相关性，从2014年—2015年2年的空间参数预报中随机提取了10个时间段的数据进行分析，按照轨道维持1个月以上的要求，对30天预报数据与实测数据的相关系数进行了统计计算。如图7所示，选取2014年8月1日年—8月30日太阳F10. 7值进行相关系数计算，可以看出预报值与实测值有明显的高相关度。

图7 太阳F10. 7预报值与实测值相关性分析

图8 地磁指数Ap预报值与实测值相关性分析

空间环境参数实测值与预报值相关系数如表1所示。根据数据统计，预报30天的太阳F10. 7数据与实测数据的相关系数平均达到0. 8以上，最高0. 984 2，可以认为预报值基本真实反应了空间环境的变化情况，而地磁Ap指数相关性较差，但是由于预报值基本反应了真实值的平均变化及趋势变化情况，这里认为可以忽略相关性的影响。因此，可以采用实测数据推算二元一次线性回归方程形式的经验公式[10]，以描述轨道周期变率与太阳活动和地磁的数值关系[11]，并进一步用实测数据对此结论和预测进行验证。

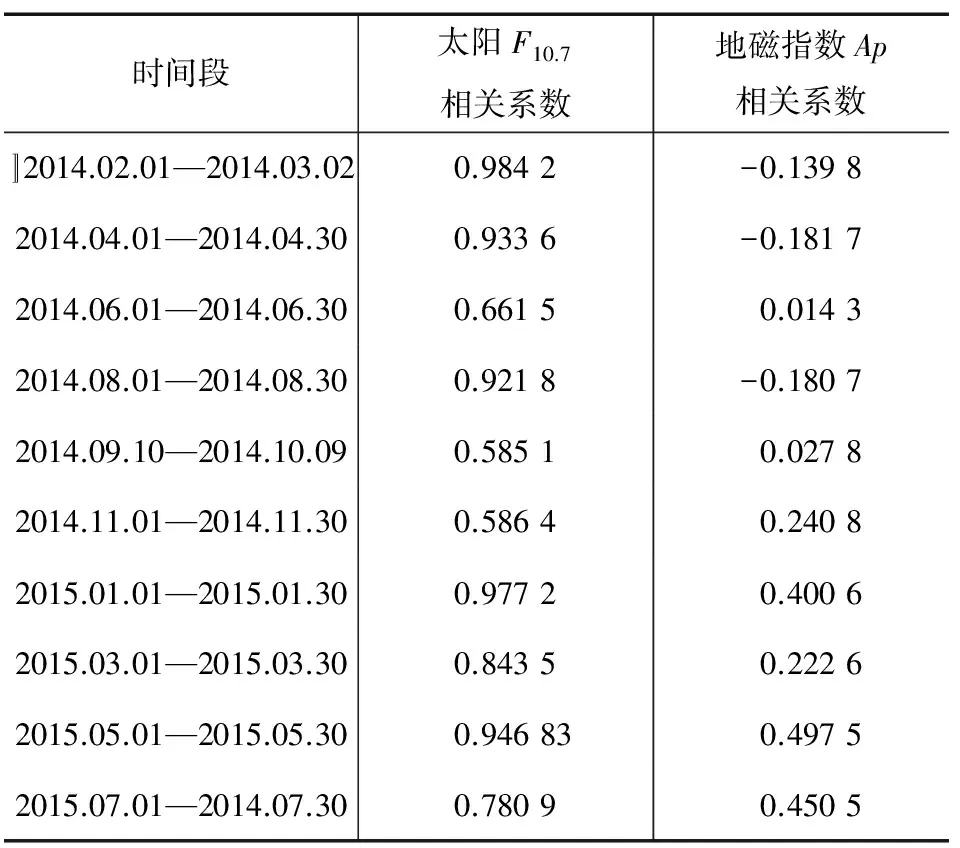
表1 空间环境参数实测值与预报值相关系数

3 空间环境预报数据与周期变率反演公式

某型卫星轨道周期变率与太阳F10. 7和地磁Ap指数的经验公式求解如下：建立1个二元一次回归方程，使用回归精度较高的最小二乘法解算系数[12]。2个自变量为x1和x2，其中x1是太阳F10. 7，x2是地磁Ap指数，轨道周期变率作为因变量y。

一组测量数据(x1i，x2i，yi)在三维图上求出其最小二乘平面，各试验点距离该平面的偏离平方和E为[13]：

(1)

式中，回归参数a0，a1，a2应该是当E最小时的估计量，将E分别对a0，a1，a2求导，并使其倒数为零，以得到下列方程组：

(2)

由于

y=a0+a1x1+a2x2，

(3)

(4)

故

(5)

可以写成

(6)

(7)

(8)

(9)

(10)

(11)

本文以2次轨道维持之间的时间段内的一段数据按照上述方法进行了解算，得到了这个时间段内的经验公式，由于空间环境变化受季节性影响较大，不同阶段经验公式可能有一定区别[15]，在需要时可根据现有公式进行试算，快速得到轨控日期季节时间的经验公式。以下是2014年8月1日—19日期间的经验公式：

y=-456. 418 7+3. 814 3x1+2. 100 9x2。

(12)

另外，在前面的图形分析中，可以看出轨道衰减值的较大变化相对太阳F10. 7和Ap指数峰值出现的时间有一定的延迟，平均延迟4～6天左右，在采用这些公式的时候，也需将相应的日期推后5天左右。

4 公式验证

选取上述经验公式时间段内的空间环境参数预报值，代入公式，并将求得的轨道周期变率结果与实际测定结果进行比较，进而分析经验公式的准确性与可靠性，如图9所示。计算结果反应了实测值的变化规律，并且在有周期变率突然变化的情况下能够反应整体平均值的真实情况，验证了公式的正确性。因此，利用本文得出的经验公式，结合空间环境预报，可以对轨控后的周期变率进行预报，制定轨控策略过程中，按控后周期变率进行轨迹网预报，真实地反应控后轨道变化的实际效果。

图9 周期变率实测值与经验公式计算值对比结果

5 结束语

结合某型卫星轨道控制过程中空间环境突然恶略变化导致的轨迹网维持时间不满足预期的情况，给出了问题的分析方法和过程，以及太阳活动和地磁活动对轨道周期变率的影响分析，通过数据融合分析给出了三者之间的经验公式，并利用实测数据对公式进行了验证。结果证明，利用经验公式可以对轨控后一段时间的轨道周期变率进行预报，在轨道保持周期时间内具有可信性，有效地改进了轨控策略制定的精确度，在一定程度上解决了空间环境对轨控效果的影响，亦可将这种研究方法推广到其他类型的数据分析中。下一步对于经验公式的总结仍需积累大量数据，对不同季节变化规律进行统计分析，分时间段得到不同的经验公式，方便日后应用。