基于Neumann展开随机有限元的混凝土重力坝结构可靠度分析

程 井,韦锦鹏,李宗樾,李培聪

(1.河海大学水利水电学院,江苏 南京 210098; 2.贵州省大坝安全监测中心,贵州 贵阳 550002)

尽可能地模拟真实情况并对结构的各种不确定性进行量化分析,一直是结构仿真分析的核心任务。早期水工结构设计中一般采用安全系数方法来考虑结构的安全性。随着随机力学的发展,视材料参数为随机变量的可靠度理论如一次二阶矩、验算点法、响应面法等方法逐渐应用于水工结构,使得结构安全评价更为准确[1]。然而实际工程结构的材料特性是随时空分布的随机场,传统随机变量模型假定研究尺度内任意两点处的参数之间完全相关,这种假定对于很多情况可能会导致较大的偏差。因此,为了更准确地估计结构的可靠度,须建立参数的随机场并运用随机有限元方法来求解[2-3]。

随机有限元产生于20世纪70年代左右,主要分为蒙特卡洛(Monte-Carlo)随机有限元法、泰勒展开随机有限元法、摄动随机有限元法等[4]。1972年Shinozuka[5]将有限元与Monte-Carlo方法相结合进行分析。随后,Dendrou等[6]在研究岩土工程中的不确定性问题时,将位移响应量在随机变量的均值点处进行泰勒展开并计算位移的一、二阶响应量。1981年,Hisada等[7]提出了摄动随机有限元法,该方法考虑随机变量在均值点的微小摄动,代入有限元方程进而推导出位移的均值与方差。我国杨杰等[8]研究了摄动的变分列式解的存在性和唯一性,并给出了明确的误差界,指出了摄动随机有限元的适用范围。李典庆等[9-10]考虑土的空间变异性,运用随机有限元对土的边坡可靠性进行了分析。单一的Monte-Carlo随机有限元法概念简单,易于实现,且不受随机变量波动范围以及结构的影响,但计算量十分大,不适用于大型工程的计算,为此研究者提出了不同的优化方法[11-12]。

针对混凝土重力坝工程中材料特性空间分布的随机性问题,笔者将Monte-Carlo方法与Neumann级数展开随机有限元法相结合,提出了混凝土重力坝可靠度计算方法,并研究了相关偏度和随机场离散单元尺寸对可靠度的影响。

1 随机场离散的局部平均法

随机场离散的目的是将随机场离散为随机变量。随机场离散方法有很多,主要有中心点法、局部平均法、形函数插值法等。对于均匀随机场,中心点法简单方便,但精度较差、效率低。本文运用局部平均法来离散随机场。对于一维随机场X,单元长度为T的均一化单元离散方案时,有如下方差公式[13]:

(1)

式中:σT为平均随机场XT的方差;σX为原随机场方差;γ(T)为方差折减系数。

对于二维连续均匀随机场α(x,y),其均值和方差分别为m和σ2,往往采用一般形状的四边形单元或三角形单元来离散,并可以采用与有限元等参变换类似的方法。单元e的局部平均随机场αe为

(2)

式中:Ae为单元e的面积;Ωe为单元e所占有的区域。

随机场均值m为

(3)

式中：E(αe)为αe的期望。

单元e和单元e′的局部平均随机场的协方差为

(4)

式中:ρ为相关函数;上标′表示单元e′的变量。

对式(4)作等参变换可得

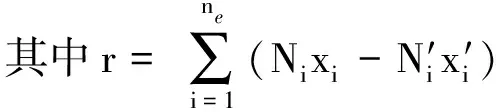
式中:ne为单个单元节点数;xi、yi分别为单元e的第i个节点在x、y方向上的坐标;Ni为形函数;J为雅克比矩阵;ξ、η为x、y作等参变换后的变量。对随机场内所有单元进行上述计算即可获得整体的单元平均随机场协方差矩阵。

为计算方便一般视二维均匀随机场相关结构可分离,即

ρ(r,s)=ρ(r)ρ(s)

(6)

随机场相关结构常采用的相关函数形式有非协调阶跃型、协调阶跃型、三角型、指数型、二阶AR型、高斯型等。本文选取如下指数型进行计算：

(7)

式中:θ为相关偏度;τ为两点间距离。

2 Neumann 级数展开随机有限元

对于静力问题,有限元平衡方程可写为[14]

KU=F

(8)

其中K=K0+ΔK

式中:K为系统整体刚度矩阵;F为确定性外荷载列向量;U为结构位移列向量;I为单位矩阵；K0为均值弹性模量时的系统整体刚度矩阵;ΔK为系统整体刚度矩阵的增量。

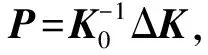
(I+K0-1ΔK)-1=I-P+P2-P3+…

(9)

U0-PU0+P2U0-P3U0+…=

U0-U1+U2-U3+…

(10)

其中K0U0=F

Ui=PiU0=PUi-1(i=1,2,…)

先求出U0,根据递推关系(式(10)),最终求得结构位移列向量U。Neumann展开阶数可依据下式的收敛标准来确定:

(11)

式中:k为级数收敛时展开阶数;ε为误差上限，ε应小于0.05。

3 重力坝结构可靠度计算

重力坝可靠度计算内容主要包括位移、应力及抗滑稳定可靠度。首先依据材料空间分布特性,将坝体材料随机场进行单元离散;对于生成的局部单元平均随机场协方差矩阵,通过Monte-Carlo方法进行随机抽样,形成N组样本;对于每组样本,采用基于Neumann展开的随机有限元方法进行计算求解,获得N组位移、应力等响应量,进而算得各物理量的均值及方差;根据实际工程问题,依据相关准则,建立包含位移或应力的功能函数[1],并代入之前的计算结果,即可得到各种功能条件下的可靠度。

采用Monte-Carlo方法与Neumann级数展开相结合时,由式(10)可知,无论模拟多少次都只需进行一次求逆过程,极大地提升了运算速率。

4 算例分析

基于Matlab开发了相应随机场离散及随机有限元程序;通过典型算例对本文方法进行验证,并运用该方法研究随机场单元尺寸和相关偏度对可靠度的影响以及计算重力坝坝踵抗拉可靠度。

4.1 算例1

长5 m、宽0.5 m、厚0.3 m的悬臂梁结构,右端承受集中荷载15 kN,左端固定,不计自重。其弹性模量是均值为30 GPa的随机场,变异系数为0.1,相关偏度取2 m,泊松比为0.167。随机有限元计算时,随机场单元划分及有限元网格划分分别见图1(a)和图1(b)。

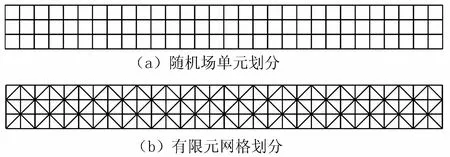
图1 随机场单元划分及有限元网格划分

Neumann级数展开阶数取3,模拟20万次可得悬臂梁右端点挠度的概率密度曲线如图2中带*标记的曲线所示。如设计时规定右端点的允许最大位移为13.2 mm,则其可靠度β=3.05。若使用单一的Monte-Carlo方法,则计算的可靠度为2.96,与本文方法的结果非常接近,表明了本文方法的正确性。

为了分析相关偏度对计算结果的影响,针对同一悬臂梁同一随机场划分(见图1(a)),采用不同相关偏度θ进行敏感性分析,计算得出的悬臂梁右端挠度概率密度如图2所示。经计算,当相关偏度取2 m、5 m、50 m、500 m时,可靠度分别为3.05、2.23、2.02、1.98;当随机场完全相关(将整个随机场视为单个随机变量)和相互独立时,可靠度分别为1.96、5.00。这些结果表明:随着相关偏度的减小,所得的位移响应量更趋于集中,可靠度逐渐增大;完全相关时可靠度最低,但实际坝体情况不可能为单一随机变量,而是随机场变量,因此仅将坝体弹性模量视为单一随机变量时所得可靠度较实际值低。

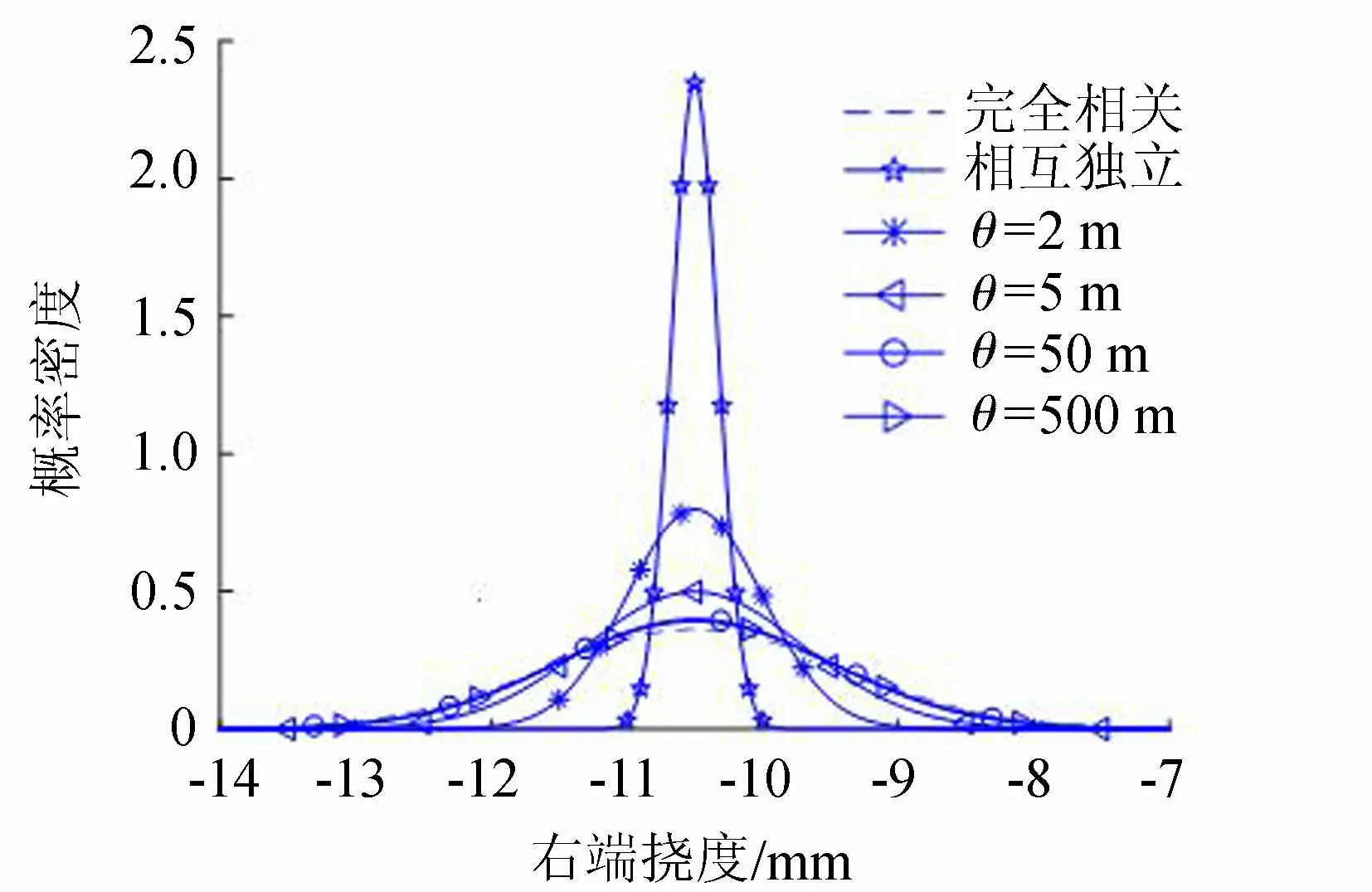
图2 不同相关偏度下悬臂梁右端挠度概率密度曲线

4.2 算例2

采用局部平均法离散随机场时,不同的随机场单元划分会影响方差的折减,进而对可靠度计算产生影响。设计如下算例,探讨随机场单元划分对结构可靠度的影响。

悬臂梁结构长2 m、宽0.1 m、厚0.1 m,右端承受集中荷载3 kN,左端固定,不计自重。随机场材料特性参数同算例1,相关偏度为0.5 m,结构有限元沿长度方向等分为120个单元。采取不同随机场单元长度时的平均随机场方差折减系数结果如图3所示。Monte-Carlo方法模拟5万次,以22 mm为右端点允许最大位移时,计算结果表明可靠度随随机场单元的加密而逐渐增大;当相关偏度与单元尺寸的比值(θ/T)取2、6、8、10、15、30时，可靠度分别为2.52、2.58、2.61、2.62、2.62、2.62，可见当θ/T大于8～10时,计算结果趋于稳定,因此建议随机场单元尺寸取值不大于相关偏度的1/10～1/8。

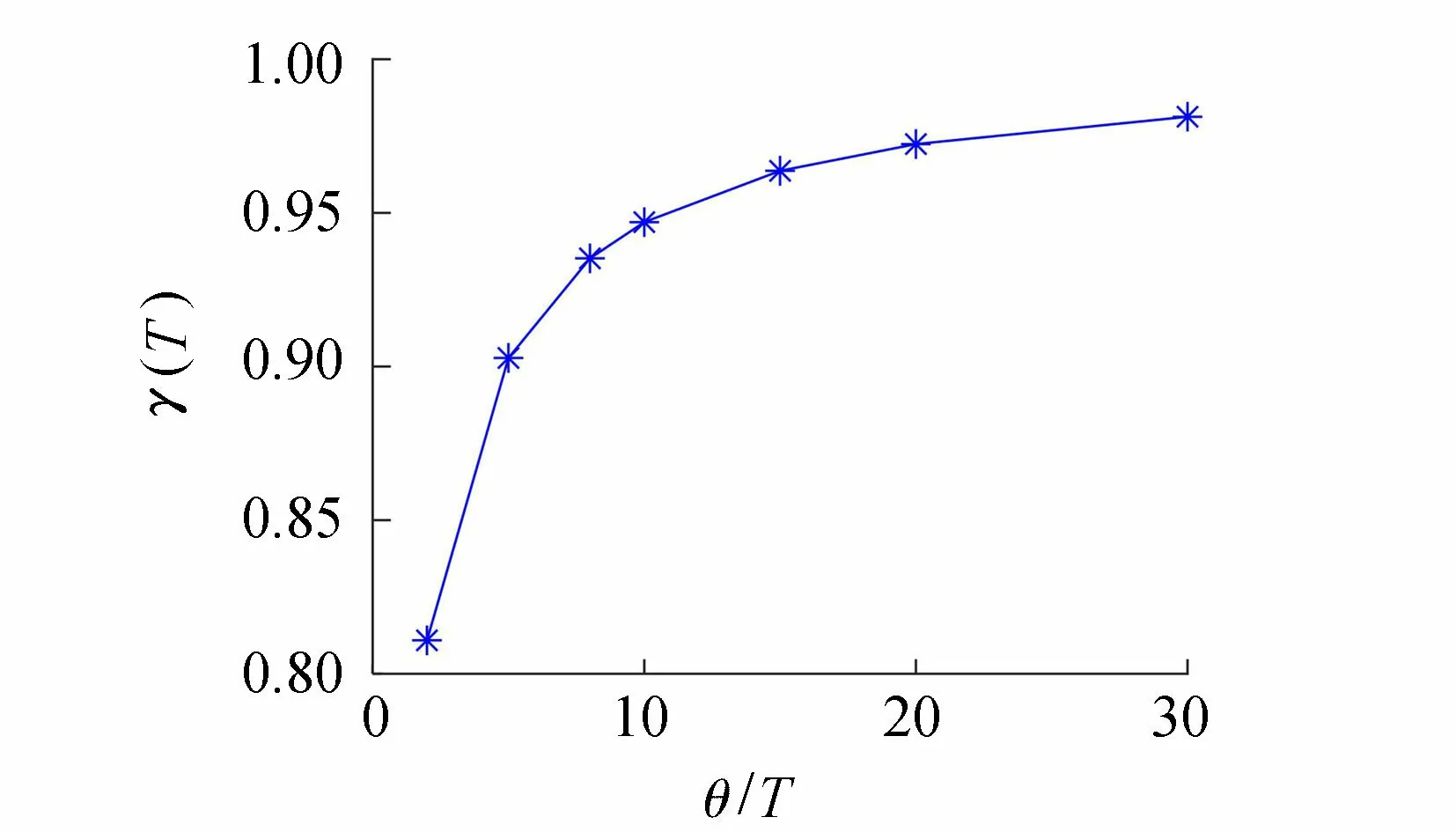
图3 θ/T与γ(T)关系曲线

4.3 算例3

典型重力坝坝顶高程为382 m,最大坝高为166 m,坝基高程为216 m,坝底宽度B为145 m,上游正常蓄水位为377 m。坝体混凝土弹性模量视为随机场,均值取20 GPa,变异系数为0.2,相关偏度取70 m。为计算方便,随机场与有限元共用同一网格,单元480个,节点533个,如图4所示,其中x向为顺河向,以指向下游为正;y向为竖直方向,以向上为正。随机有限元计算时,Monte-Carlo方法的模拟次数取10万次,Neumann级数展开阶数取3阶。

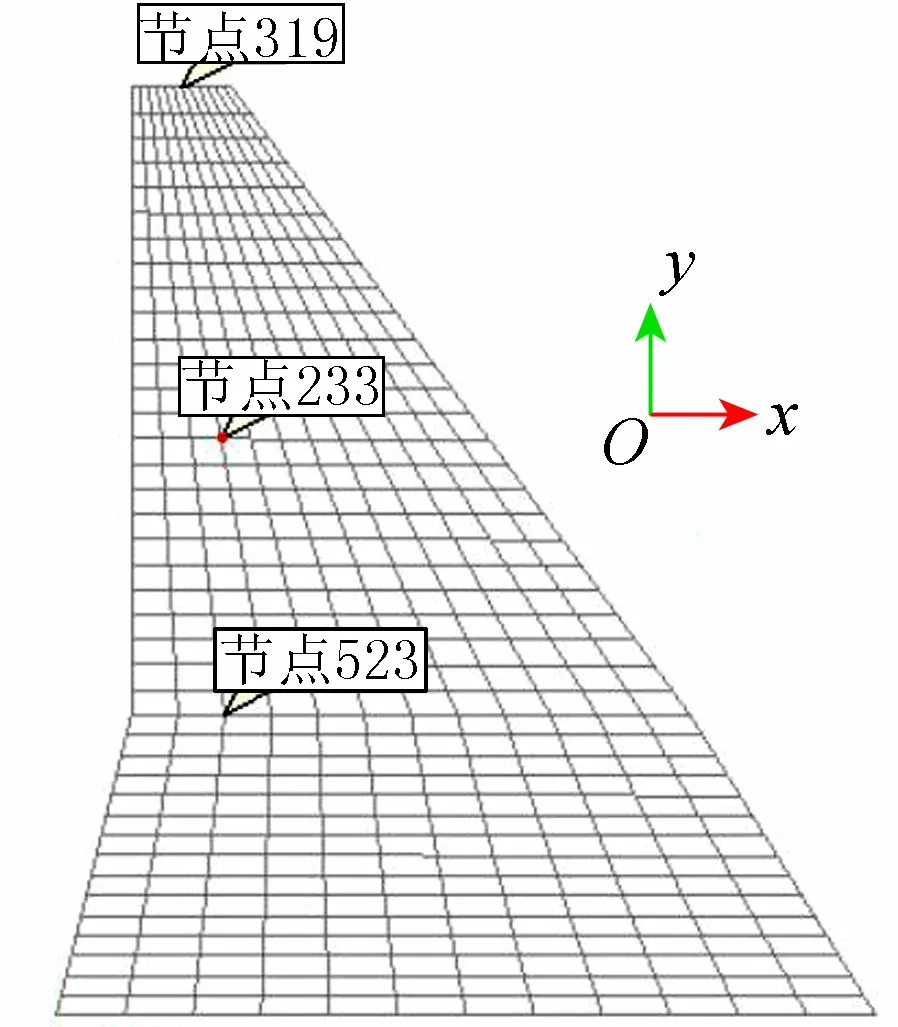
图4 重力坝随机场与有限元划分

正常蓄水位情况下,重力坝水平及竖直向位移均值云图分别见图5(a)和图5(b),竖直向应力云图见图6,图4中3个节点的顺河向位移概率密度曲线见图7。大坝设计时需满足一定的应力要求。根据NB/T 35026—2014《混凝土重力坝设计规范》和GB 50199—2013 《水利水电工程结构可靠性设计统一标准》,采用线弹性有限元法计算坝踵垂直应力且计扬压力时,拉应力区宽度应小于坝底宽度的7%。本算例中统计了坝底距上游面0.07B处节点的竖直向应力,其概率密度曲线见图8,据此可计算出基于规范拉应力范围控制的大坝坝踵抗拉可靠度β=3.7。

图5 重力坝不同方向位移均值云图(单位:mm)

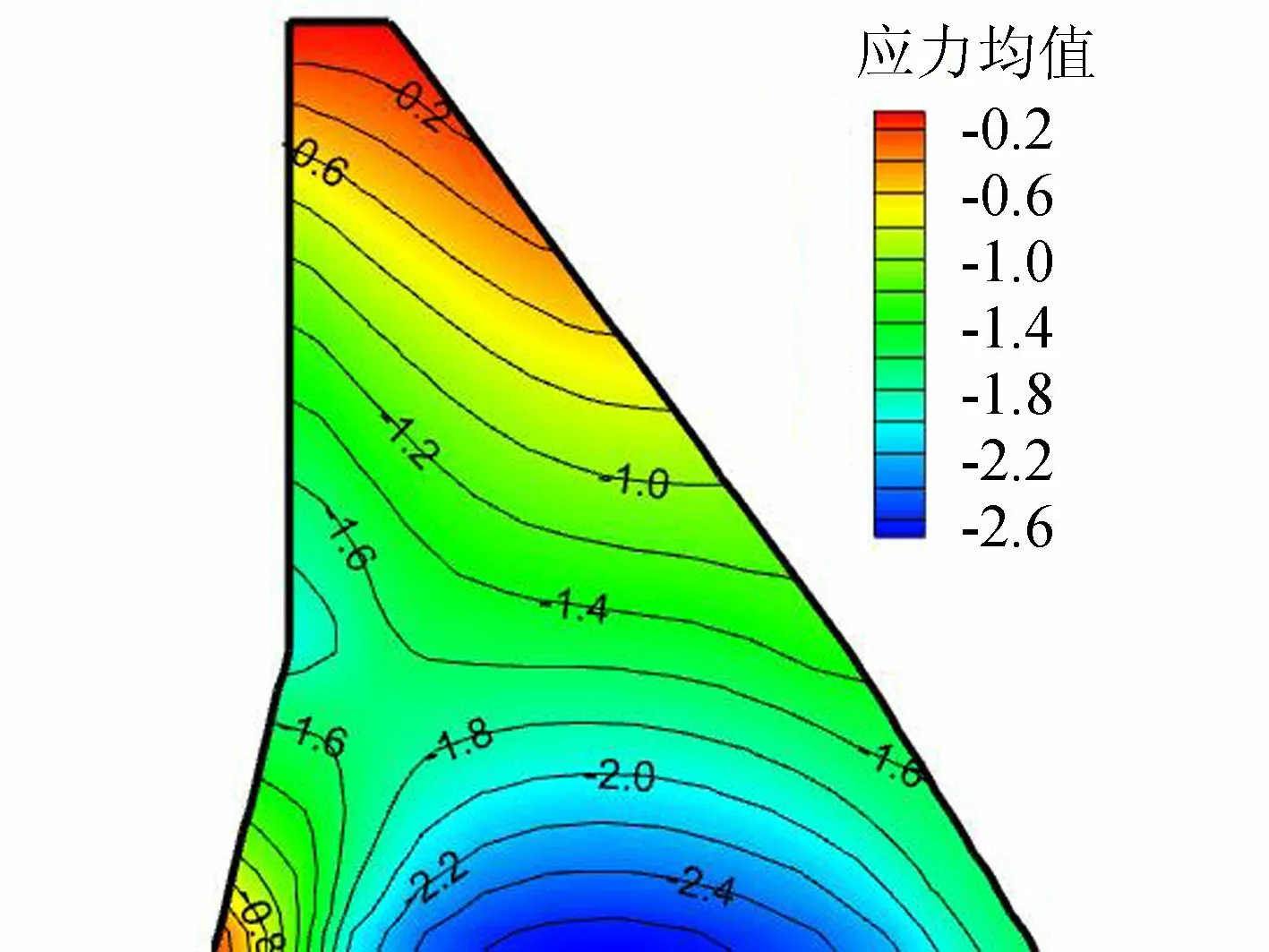
图6 重力坝y向应力均值云图(单位:MPa)

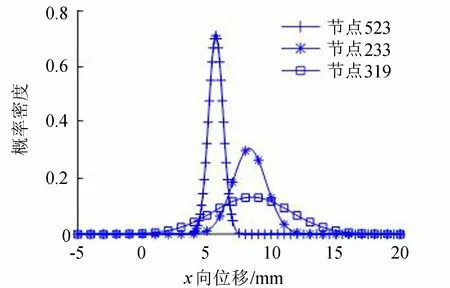
图7 选取节点x向位移概率密度曲线

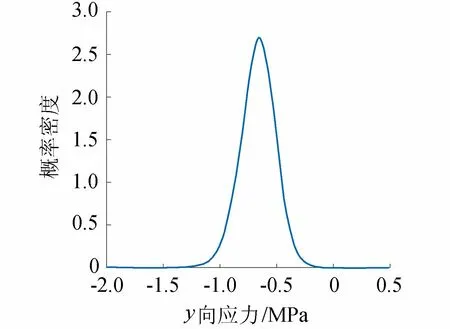
图8 7%坝底宽度处y向应力概率密度曲线

5 结 语

本文提出了基于Neumann展开随机有限元的混凝土重力坝结构可靠度计算方法,采用算例验证了方法的正确性,并分析了相关偏度和随机场单元划分对可靠度的影响。结果表明:①本文方法能较好地模拟材料的空间变异性,所得结果符合实际情况;②随机场相关偏度反映了材料的空间离散程度,其取值对大坝的可靠度结果影响显著,可靠度随相关偏度的减小而增大,如将坝体弹性模量视为单一随机变量,则所得可靠度较实际值低;③随机场单元尺寸不能过大,建议取值不大于相关偏度的1/10～1/8。

为进一步提高该方法在实际工程中的计算精度,还需开展如下工作:①大坝算例中将坝体视作一个均匀随机场,实际工程中存在不同的工程分标及材料分区,且不同分区间又具有一定的相关性,需要建立更加细致的随机场模型;②相关偏度或相关结构对计算结果影响显著,但缺少这方面的工程资料,且如何获得相关偏度值及描述相关结构的相关函数形式也缺乏统一明确的标准。