磁悬浮轴承转子自适应模糊滑模控制研究

李 莹,欧阳名三,徐 冬

( 安徽理工大学电气与信息工程学院, 安徽 淮南 232001)

由于磁悬浮具有无摩擦、无须润滑、低耗能、高精度等优点，被广泛应用于航空、军事、精密加工等领域。然而，磁悬浮轴承转子电磁力与输出电流之间存在严重的非线性，难于建立精确的电流和电磁力精确数学模型，且易受干扰的影响。国内外学者对磁悬浮控制方法进行了大量的研究，传统的控制方法是在磁悬浮系统满足线性化条件下，在平衡点附近对磁悬浮模型进行了线性化，并采用线性控制方法[1-7]，极大地限制了磁悬浮系统的工作空间。

由于滑模控制是一种本质非线性控制，对系统的干扰具有不变性，广泛应用于磁悬浮轴承控制中[8-11]。然而，以上方法都需要建立电磁力与电流的关系模型。本文主要对磁悬浮径向磁轴承某一自由度方向上的磁悬浮转子运动控制进行研究，针对磁悬浮轴承转子所受电磁力与电流之间存在复杂非线性，且整个磁悬浮轴承系统易受干扰影响，提出采用滑模变结构方案设计控制器，将非线性光滑函数引入到趋近律的设计中。本方案不需要建立磁力与电流之间的复杂关系模型，采用模糊自适应控制对系统中不确定的部分进行辨识。

1 磁悬浮轴承转子动力学模型

本文以径向磁力轴承为研究，并以转子竖直方向一个自由度的情况进行研究，平衡位置时的位移为0mm，转子与磁铁之间的间隙C0为0.3mm，即转子振动幅值超过0.3mm转子就已经开始碰撞轴承，这会造成磁悬浮转子系统的破坏。差动磁力轴承结构如图1所示，当转子位于轴承几何中心位置时，为了建立起磁场，在上、下磁极线圈中通有相等的电流I0，I0被称为偏磁电流。

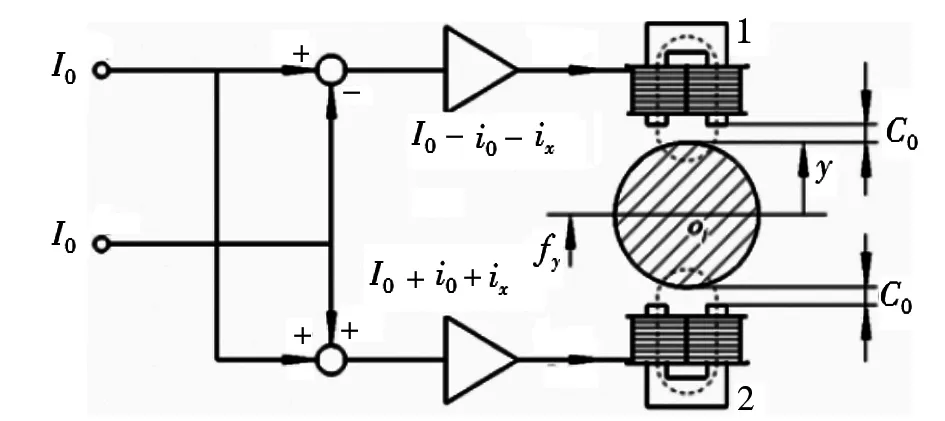
图1 磁力轴承结构简图

在静平衡状态时，fy0和转子自重平衡。此时，期望转子静态悬浮于轴承的几何中心，则应有

(1)

(2)

系统在静平衡时，平衡转子自重的电磁力是依赖静态反馈电流i0维持的。

当转子受到扰动偏离静平衡位置时，如转子向上运动则转子与上磁铁之间的气隙为C0-y；相应地，转子与下磁铁之间的气隙为C0+y。

当电磁铁与转子之间的气隙很小时，假设电磁铁转子、钉子和气隙中的磁场分段均匀分布，铁芯呈现不饱和特性且不考虑漏磁和磁滞等因素的影响，于是一对磁极间所产生的电磁合力为

(3)

式中：C0为转子外表面与径向轴承定子内表面间的气隙，A0为气隙横截面积，μ0为真空磁导率，N为线圈砸数，ix为反馈电流。

以转子的静平衡点为基点，建立竖直方向磁悬浮动力学模型为

(4)

将式(2)及(3)带入(4)，得

(5)

(6)

式中：f(y1，y2，ix)为电磁力模型及系统不确定项，d为有界扰动项。

式(6)的等价模型为

(7)

式中：h(y1，y2，ix)=f(y1，y2，ix)+d-c0ix。

2 滑模控制器的设计

控制器的设计目的是设计控制电流的大小ix，使磁悬浮系统稳定在平衡点(即磁悬浮的几何中心)位置。

设滑模面函数为

s=c1y1+y2

(8)

则

(9)

采用非线性光滑函数设计滑模趋近律为

(10)

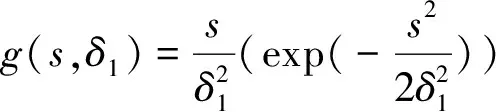
g(s，δ1)，f(s，δ2)均为光滑函数[9]。

可得模糊控制律为

ix=-c2g(s，δ1) /c0-c3f(s，δ2) /c0-

h(y1，y2，ix) /c0-c1y2/c0

(11)

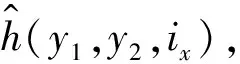
3 自适应模糊辩识器的设计

3.1 模糊系统设计

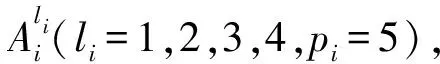
式中，li=1，2，…，5；j=1，…，25。

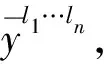
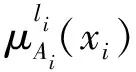
其中

(12)

3.2 自适应模糊变结构控制器设计

(13)

式中：y为模糊向量，θh参数根据自适应律而变化。

自适应模糊滑模变结构控制系统结构如图3所示。

图3 控制系统结构图

3.3 稳定性分析

设最优参数为

(14)

将式(13)带入式(9)得，

(15)

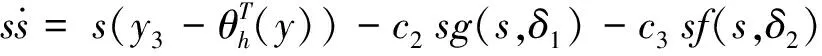
由于模糊系统可以以任意精度逼近未知系统，即

(16)

则式(15)为，

(17)

由式(17)可知，只要满足下列不等式

|s|ε≤c2sg(s，δ1)+c3sf(s，δ2)

(18)

满足Lyapunov稳定性定理，因此，滑模控制系统是大范围渐进稳定的。

4 仿真分析

本文针对磁悬浮轴承转子由静止状态到悬浮平衡位置进行仿真研究。磁悬浮轴承、模型各参数如表1所示。 增益参数初始值c0=2，c1=1，c2=c3=10。假设系统的输出状态在(2.0×10-3，1.0×10-4)位置，仿真时间为1s。 系统状态稳定过程、稳态误差及相轨迹如图6～图9所示， 转子0.5s内即可稳定在平衡点， 稳态误差为0.022mm， 相轨迹曲线体现了本文方法较好地解决了滑模的抖振问题。

表1 模型计算参数

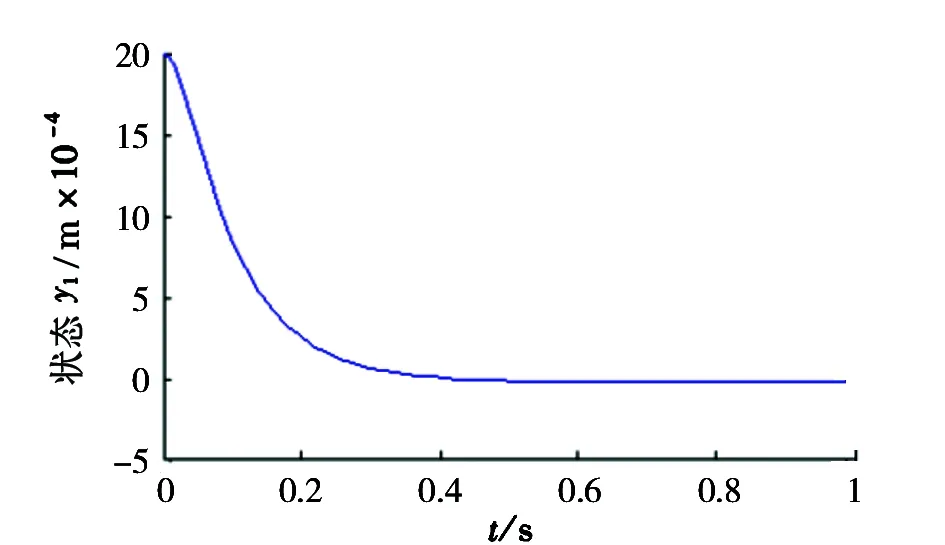
图4磁悬浮状态y1运动过程曲线

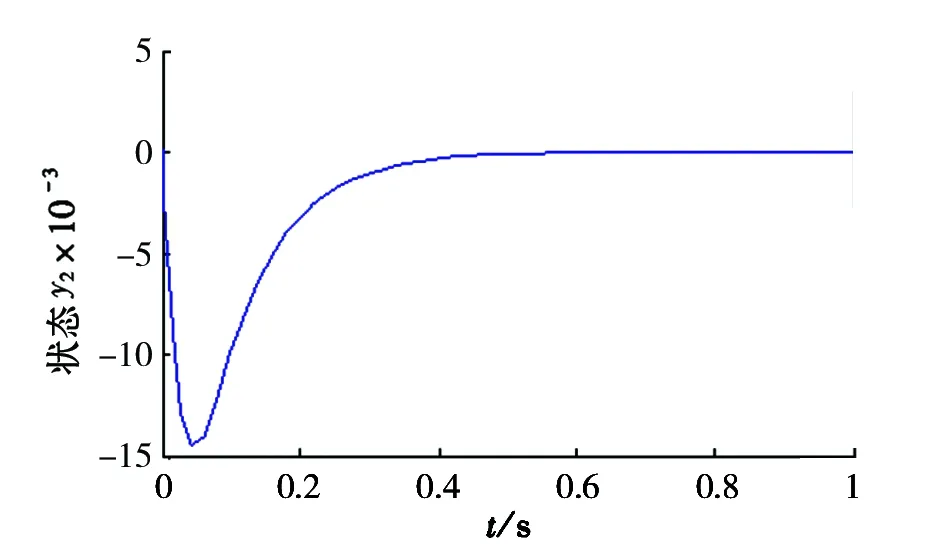
图5磁悬浮状态y2稳定效果图

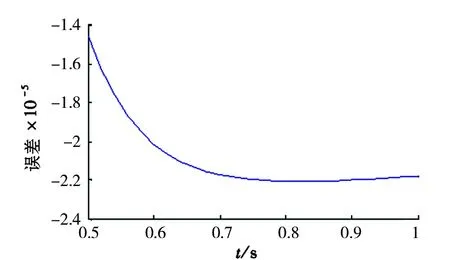
图6 误差曲线

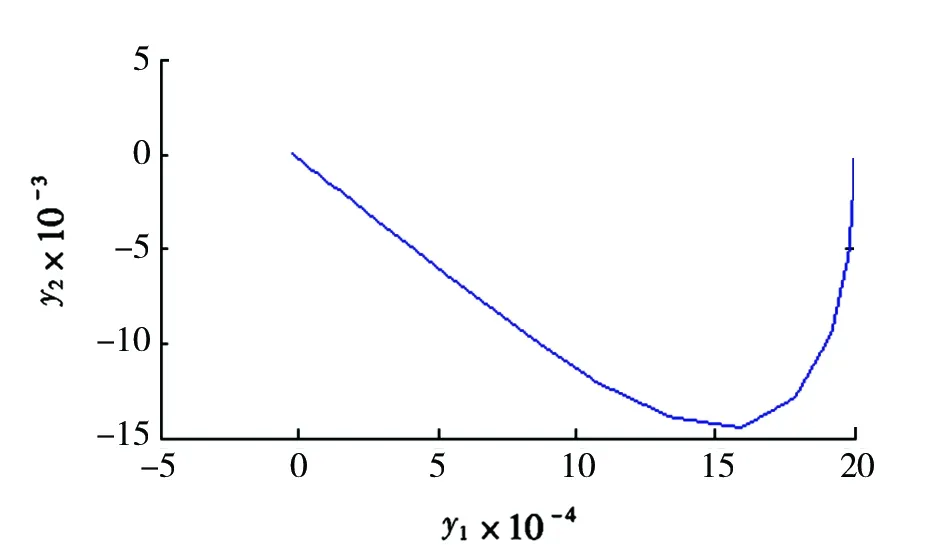
图7 磁悬浮转子运动相轨迹图

图8 模糊辨识电流及力模型

图8为模糊辨识系统电流与力模型，电流与力模型近似为线性化模型，此结果与在小电流变化范围内可将电流与力关系模型进行线性化处理相吻合。

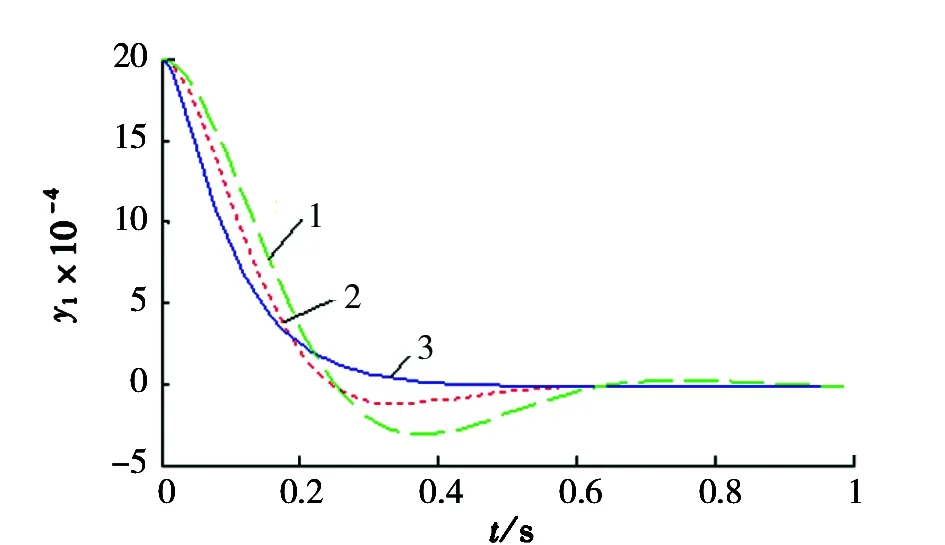
1. 26kg；2. 16kg；3. 6kg图9 不同转子质量系统状态输出曲线

图9为转子质量分别取为6kg、16kg、26kg时，控制参数不变的情况下，转子状态变化曲线图。由图11可知，随着转子的质量不断增加，系统稳定的调节时间越来越长，但最终都能稳定在平衡点附近。

1. 3mm；2. 4mm；3. 4.5mm；4. 5mm图10 不同间隙系统状态输出曲线

图10为转子与定子之间单边间隙分别取为3mm、4mm、5mm时，控制参数不变的情况下，转子状态变化曲线图。由图10可知，随着气隙不断增加，系统稳定的调节时间越来越长，稳定误差逐渐增大，随着气隙的增加，转子出现震荡现象，转子仍在安全范围内运动。

图11为在系统运行0.1s突然加一阶跃干扰项，状态的变化曲线，由图11可知，系统并未受到干扰较大的影响，快速地稳定在未受干扰干扰前状态曲线上，体现了该方法具有较好的鲁棒性。

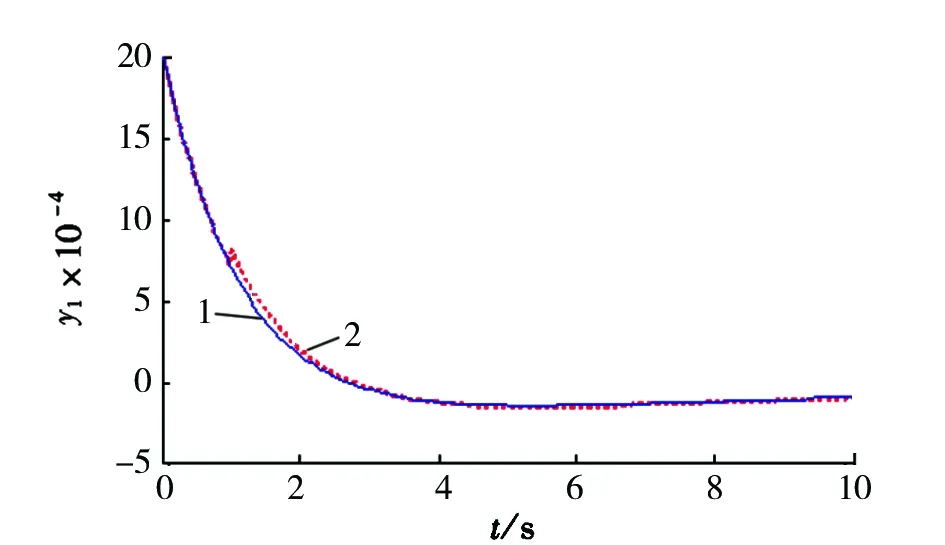
1. 无干扰；2. 干扰图11 有无干扰系统状态y1的变化曲线

5 结论

(1)基于径向磁悬浮轴承转子某一方向的单自由度磁悬浮轴承转子动力学模型进行研究；将滑模变结构控制设计思想应用到了磁悬浮轴承转子控制器的设计中；将磁悬浮轴承转子电磁力与电流之间的关系看为不确定项，基于非线性函数建立滑模系统的趋近律，采用自适应模糊系统在线进行辨识，从而设计控制律，并通过Lyapunov理论论证该设计方案在大范围内是渐进稳定的。

(2)利用Simulink数值仿真工具，对磁悬浮轴承转子的模糊自适应滑模变结构控制系统进行验证与分析。给出了磁悬浮不确定模型的自适应模糊系统的辨识曲线，详细分析了结构参数质量、间隙对磁悬浮轴承转子系统的影响，为磁悬浮转子系统的结构设计提供依据。