基于J-C模型的45钢本构参数识别及验证
魏 刚, 张 伟, 邓云飞
(1. 中国民航大学 航空工程学院, 天津 300300; 2. 哈尔滨工业大学 航天学院高速撞击动力学实验室, 哈尔滨 150001)
随着计算机和数值计算方法的发展,数值模拟成为研究工程中结构的大变形甚至材料和结构破坏问题的重要手段,但是材料的动态本构关系一直是束缚其发展的瓶颈[1]。在进行数值仿真研究中,合适的材料本构模型和准确的模型参数是保证仿真结果准确性的关键。Johnson-Cook(J-C)本构模型[2]由于形式简单,物理意义明确,参数获得相对容易,已经在延性金属材料的动态性能描述方面获得了许多成功的应用。
45钢是一种性价比较高的优质碳素结构钢,使用范围较广泛。除了用来做模具的模板、导柱外,还经常用于制作承受负荷较大的小截面调质件和应力较小的大型正火零件。综合机械性能较好是45钢的特性,但未经热处理的45钢表面硬度低,不耐磨。如果需要较高的表面硬度,可以对45钢进行调质和表面淬火来使工件的表面硬度得到提高,对心部强度要求不高的表面淬火零件常见的有曲轴、传动轴、齿轮、蜗杆、键、销等[3]。通过改善热处理工艺,可以得到性能更优良的45钢材料。也正因为如此,45钢的力学性能和热处理状态密切相关,不同热处理状态下得到的45钢性能差别会非常大。
胡昌明等[4]对45钢在不同温度和不同应变率下的力学性能进行了研究,对J-C模型进行了轻微修改,获得了本构模型参数。同时通过金相观察和透射电镜对高应变率下的材料断裂机理进行了分析。他们使用的45钢在准静态下的拉伸屈服强度仅496 MPa。陈刚等[5]运用静态试验机和SHPB装置对45钢进行了不同温度和不同应变率下的力学行为研究,拟合得到了J-C本构模型参量,并用Taylor圆柱撞击试验进行了模型验证。他们使用的45钢在准静态下的拉伸屈服强度仅为400 MPa左右。李国和等[6]采用电子万能试验机对淬硬45钢(45HRC)分别进行了准静态和动态压缩力学性能试验,采用以高斯函数表示温度效应的改进J-C本构方程拟合得到了模型参数。他们得到的准静态下的压缩屈服强度为630 MPa。汤祁等[7]利用反求方法得到了45钢J-C本构方程系数,获得的45钢准静态下的拉伸屈服强度为507 MPa。另外,金山等[8]的研究表明,当45钢的热处理条件不同时,动态力学性能也会有较大差异,因此进行45钢的动态力学性能研究时,需要明确其热处理条件。
近几年,Deng等[9-12]通过实验室撞击试验对调质处理的45钢抗杆弹侵彻性能进行了一系列研究,同时还研究了45钢杆弹在穿甲侵彻过程中的变形和破坏对穿甲侵彻性能的影响。但在对应的数值仿真研究中,邓云飞等得到的仿真结果并不是太理想,其原因可能是因为采用的材料模型参数和实际使用的材料不太相符。
本文使用的材料为经过调质处理的45钢(首先对45钢材进行高温淬火,然后通过回火处理,使其力学性能稳定),热处理方式与邓云飞等使用的45钢一致。处理完的45钢洛氏硬度大约为29 HRC。开展了常温和高温拉伸以及不同应变率下的拉伸试验,获得了流动应力与等效塑性应变,应变率和温度的关系。基于实验结果,结合Taylor撞击试验,标定了J-C模型相关参数。
断裂准则必须与适当的强度模型配合使用才有实际意义。J-C断裂准则[13]已经被证明适用于大多数延性金属材料的断裂行为预测,然而J-C断裂准则待定参数确定起来比较复杂。Teng等[14-15]的研究证明,Cockroft等[16]提出的C-L断裂准则对铝合金2024-T351的穿甲问题和铝合金7A04-T6杆弹的断裂问题能够实现较好的预测。而C-L断裂准则形式简单,仅有一个待定参数,参数获取方便,因此,本文对45钢的断裂准则也试着使用C-L断裂准则来描述。最终,通过对高速下的Taylor撞击试验中弹体花瓣开裂尺寸与形式的成功预测,证实本文采用的本构模型和断裂准则及相关参数在预测45钢动态断裂破坏方面是合理和有效的。
1 45钢力学性能测试
实验中所用试件均取自经调质处理的同一批45钢板上。常温准静态和动态(万能试验机上)拉伸试验采用名义尺寸40×10×3的板状试样;高温试验由于试验机吨位问题,采用名义尺寸30×6×3的板状试样;SHTB拉伸试验采用名义尺寸6×4×1.2的板状试样;Taylor撞击试验采用名义尺寸Φ12.6×50.2的圆柱形试件。
1.1 万能试验机拉伸试验及结果
常温准静态试验在室温(20 °C)下进行,引伸计标距为25 mm,拉伸速度2 mm/min,即名义应变率8.33×10-4s-1。高温拉伸试验拉伸速度2 mm/min,温度分别为100 °C,200 °C,400 °C,600 °C,800 °C,1 000°C。试验后获得了所有试件的载荷位移曲线,并得到了相应的屈服强度。动态拉伸试验拉伸速度分别为20 mm/min,100 mm/min,200 mm/min,400 mm/min即应变率分别为0.008 33 s-1,0.041 7 s-1,0.083 3 s-1,0.167 s-1。需要说明的是,动态试验中并未使用引伸计。
图1给出了不同温度下单向拉伸试验的工程应力应变曲线,可以看出45钢流动应力随温度明显降低。温度到400 °C时,流动应力下降了约1/4左右;温度600 °C时,流动应力下降了约2/3左右;温度达到800 °C以上时,应力已经低于常温时1/10了。这说明45钢温度软化效应非常明显。
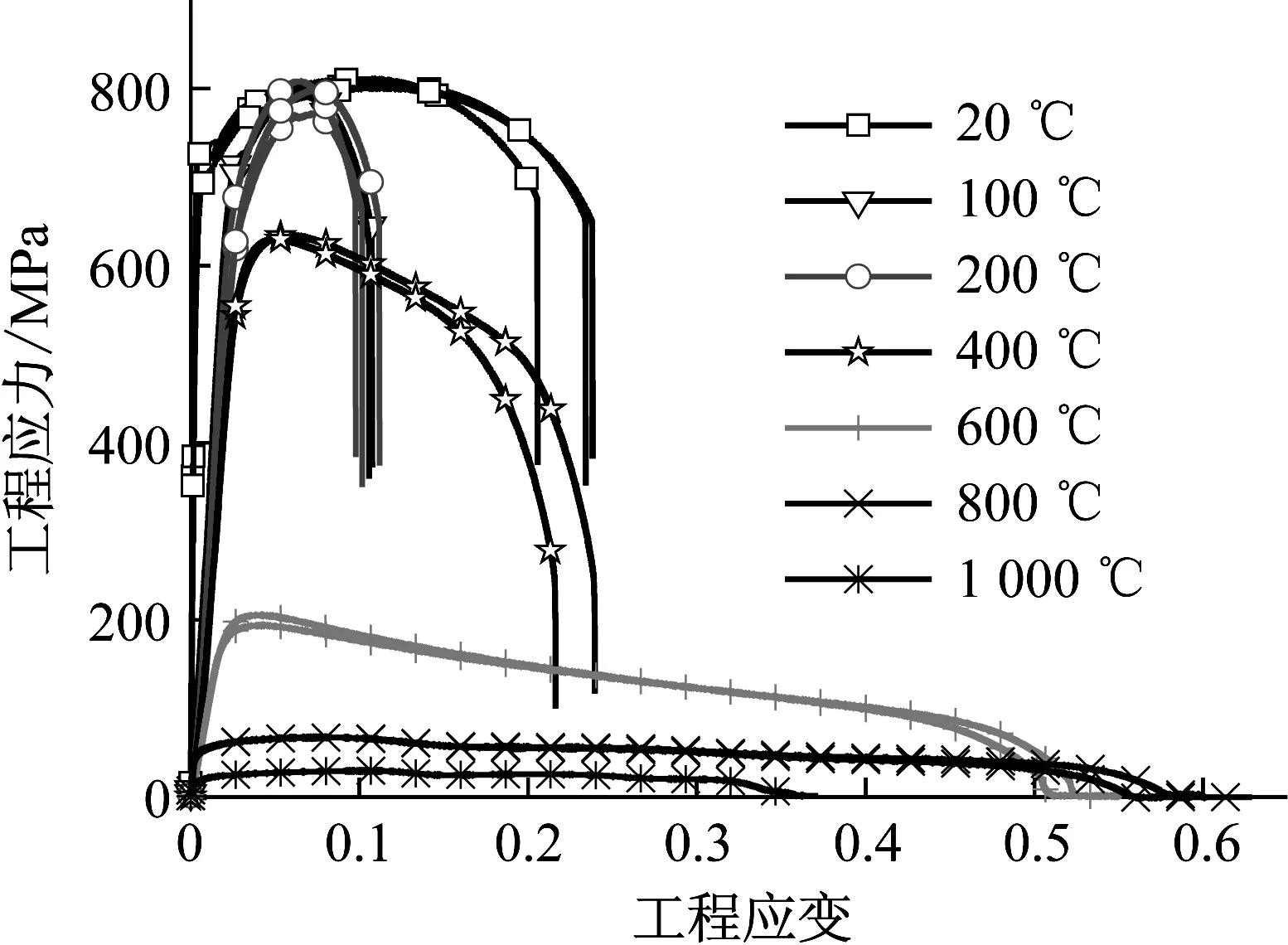
图1 45钢不同温度下单向拉伸试验工程应力应变曲线
图2给出了万能试验机上得到的不同应变率下单向拉伸试验的工程应力应变曲线(仅关注屈服强度,动态试验直线部分斜率并不是弹性模量),可以看出,在试验的应变率范围内,流动应力随应变率的增加略有增长,应变率效应不太明显。

图2 45钢不同应变率下单向拉伸试验工程应力应变曲线
图3给出了几个试验后典型的试件断口图片,可以观察到45钢断口处出现了轻微的颈缩现象,表现出了一定的韧性破坏特征。高温下颈缩现象更为明显,说明45钢随温度的升高,延性逐渐增大。

图3 45钢拉伸试样断口形状
1.2 SHTB试验及结果
为了考察较高应变率时应变率变化对45钢性能的影响,在SHTB设备上开展了动态拉伸试验,应变率从1 100~2 700 s-1。图4给出了SHTB试验得到的典型动态拉伸应力应变曲线与准静态下的单向拉伸应力应变曲线的比较。需要说明的是,在拉伸过程中,试件并未拉断。从图4可以看出,45钢有比较明显的应变率强化效应。值得注意的是,可能由于实验手段或设备的原因,再加上本文45钢强度较大,动态拉伸应力应变曲线抖动较大,不易准确得到动态下屈服强度。
1.3 Taylor撞击试验及结果
Taylor撞击试验经常被用来获取或者校准材料参数[17]。在轻气炮上进行了名义直径12.6 mm,长度50.2 mm的45钢圆柱形弹体正撞击高强装甲钢板的试验,得到了撞击后弹体长度与头部直径数据及变形破坏形式,见表1。试验中,装甲钢板未见明显变形。
表1中,m0为弹体初始质量,L0和D0分别为弹体初始长度和直径,Lexp和Dexp分别为试验后回收到的撞击后弹体的长度和头部直径,Lsimu和Dsimu分别为数值模拟中得到的撞击后弹体长度和头部直径。

图4 45钢SHTB试验与准静态拉伸工程应力应变曲线比较
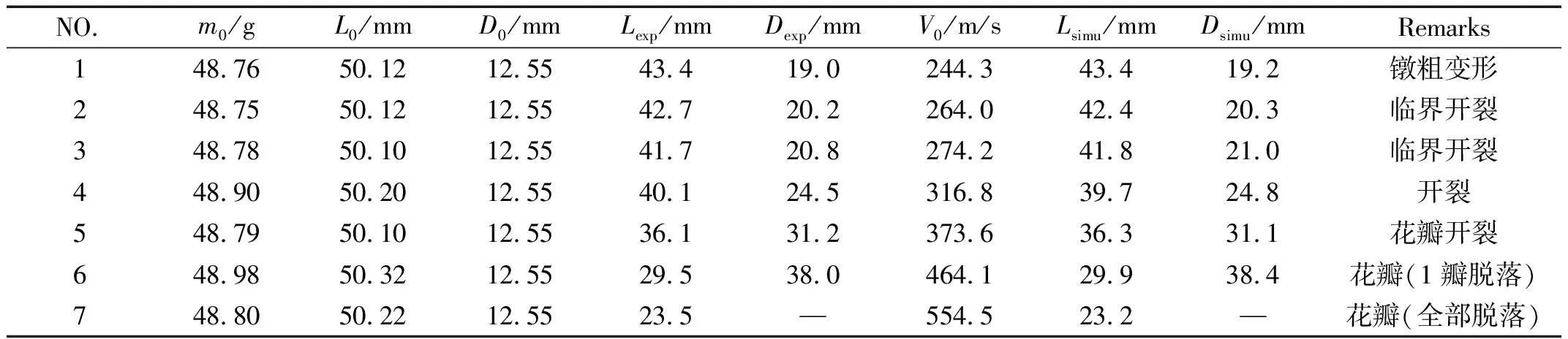
表1 Taylor撞击试验结果
2 45钢本构模型和失效准则
2.1 J-C本构关系参数标定
本文尝试在J-C本构模型的基础上描述45钢材料的力学行为。J-C模型表达式为
(1)

2.1.1 应变强化项参数A,B,n确定

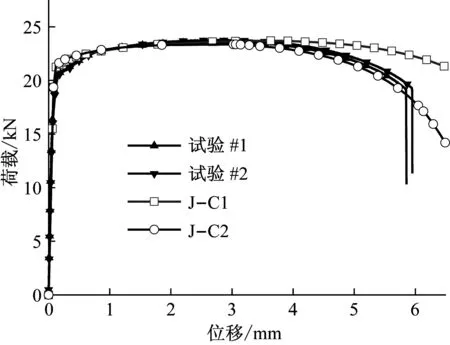
图5 J-C预测到的45钢常温拉伸下载荷位移曲线与试验对比
2.1.2 温度软化项参数m确定
从图2中可以得到不同温度下45钢准静态拉伸时的屈服强度,得到的屈服强度与温度的关系如图6所示。随着温度升高,45钢屈服强度明显减小,到800 °C以上时,屈服强度已经降到了常温时的1/10以下。
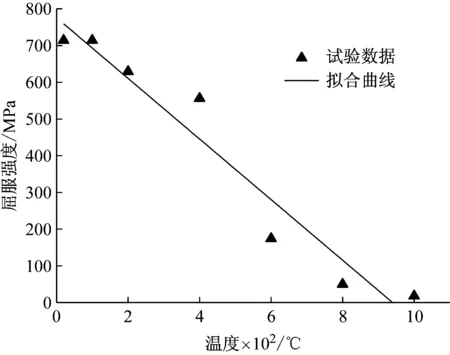
图6 45钢屈服强度与温度的关系
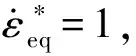
2.1.3 应变率硬化项参数C确定

对低速下动态拉伸试验,屈服强度与应变率的关系如图7所示,可以看出随着拉伸应变率升高,45钢屈服强度也在升高。用J-C本构模型中应变率项拟合可以得到,C=0.008 71。然而利用此参数对45钢Taylor试验镦粗工况进行仿真时发现,仿真得到的弹体尺寸与试验相比有比较大的差距,这可能是由于利用低速动态拉伸试验数据拟合应变率相关参数时,低估了应变率的影响,通过进行SHTB动态拉伸试验也可以证明这一点,但由于SHTB试验获得的信号抖动较大,难以准确给出屈服强度值,因此这里并没有给出SHTB动态拉伸的屈服强度值。考虑到本文要获取的本构模型参数主要用于动态变形和断裂问题的研究中,因此采用文献[1]中对2A12铝合金的处理方法,通过反算Taylor撞击试验中的镦粗工况,可以标定出C=0.037,反算结果列在了表1中。
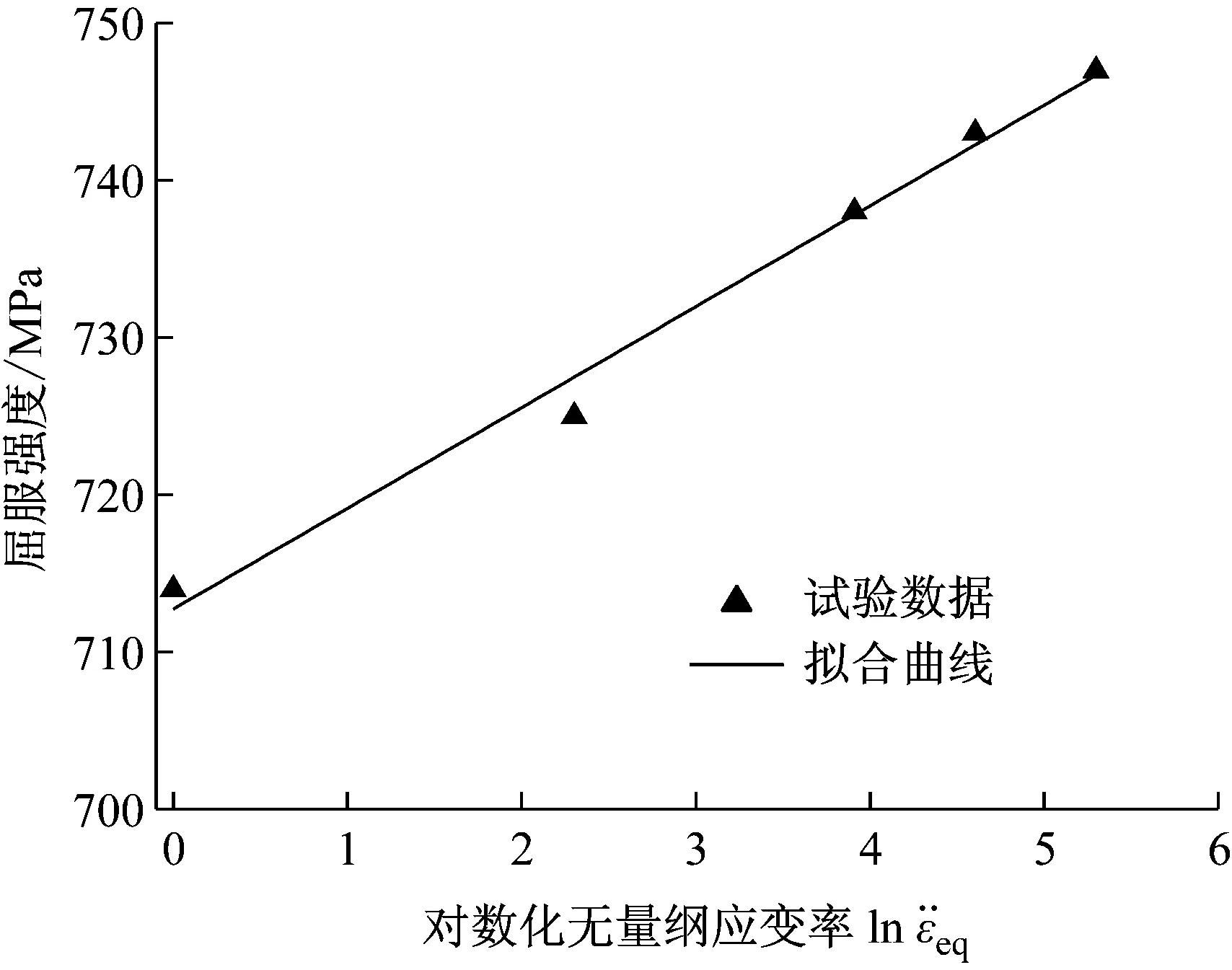
图7 45钢屈服强度与应变率的关系
2.2 C-L断裂准则参数标定
C-L断裂准则,形式如下,

(2)
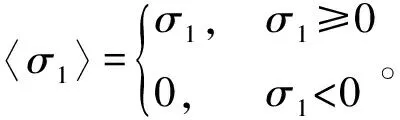
C-L断裂准则由于形式简单,只有一个模型常数Wcr需要标定,通过材料性能试验非常容易获取,且隐含了各种因素对断裂行为的影响,所以目前得到了越来越多的应用。使用C-L断裂准则获得对侵彻穿甲中的弹靶断裂问题成功预测的例子可参见肖新科[18],Børvik等[19-20],Rakvåg等[21]的工作。
本文45钢断裂准则采用仅有一个待定参数的C-L断裂准则来描述。对各条件下45钢单向拉伸试验的应力应变曲线积分,可以得到Wcr值的一个大概的取值范围,然后反算45钢Taylor试验中临界开裂的工况,可以标定出Wcr=547 MPa。反算临界开裂的试验和数值仿真结果对比图如图8所示。
2.3 模型参数的实验验证
综上,45钢本构模型和断裂准则相关参数全部得到,综合如表2所示。
利用得到的参数对较高速度下45钢Taylor撞击试验(表1中试验4~7进行数值模拟,模拟设置与2.1.3相同,弹体半径方向划分30个网格(参考文献[17])。仿真获得的形状尺寸以及断裂破坏形式与试验吻合都很好,如表1和图9所示。由此可见,本文使用的45钢


表2 45钢所有模型参数
J-C本构和C-L失效模型及获取的参数在预测45钢冲击造成的大变形和断裂破坏方面是合理可靠的。

(a) V0=316.8 m/s(b) V0=373.6 m/s

3 结 论
使用万能材料试验机、霍普金森拉杆和Taylor撞击试验,并结合ABAQUS数值仿真,研究了调质处理的45钢板材的准静态、动态及高温下的力学行为。
基于J-C本构模型,拟合试验结果,结合Taylor试验镦粗工况的反算,标定了相关模型参数;使用C-L断裂准则描述45钢的断裂行为,并结合Taylor试验临界开裂的反算,标定了模型参数。
通过对较高速度下Taylor撞击试验的数值模拟,与实验比较撞击后弹体变形尺寸与断裂破坏形式,验证了模型及参数的有效性和可靠性。
本文所得模型参量可用于调质处理的45钢结构在冲击载荷作用下的大变形和断裂破坏分析,所用方法也可用于其他金属材料力学行为的描述。

