惯导最优过程噪声参数确定及其在高铁轨道检测中的应用

周武星，朱锋，张小红

惯导最优过程噪声参数确定及其在高铁轨道检测中的应用

周武星，朱锋，张小红

(武汉大学 测绘学院，湖北 武汉 430079)

针对高精度GNSS/INS组合系统的轨道检测技术需要精确确定过程噪声参数，才能实现数据最优融合的问题，传统Allan方差方法提取的噪声参数较为粗糙。考虑到铁路轨道良好的刚性结构以及轨检小车的特殊设计，以2次独立测量中轨检小车经过同一里程点检测出的轨向偏差的重复性为评价指标，对Allan方法提取的噪声参数进行寻优，从而确定出使得轨道不平顺重复性最高的最优过程噪声参数。研究结果表明：轨道不平顺对IMU器件的角度随机游走的敏感度显著大于速率随机游走，且Allan方法的提取的角度随机游走参数较为准确，与最优配置相比不超过40%。参数调整后轨向偏差的重复性有较大改善，2趟互差标准差减小了89%。本方法对GNSS/INS轨道不平顺检测具有一定指导意义。

轨道不平顺性检测；GNSS/INS组合；Allan方差；偏差重复性；参数调整

轨道的平顺性对列车尤其是高速列车的安全运行极其重要，因而轨道不平顺检测的精度要求很高，一般在毫米级[1−2]。区别于传统的光学全站仪测量手段，基于GNSS/INS组合系统[3]的轨检技术由于能兼顾轨道检测的快速性和精确性，是近年来该领域兴起的一种全新方法，且有望成为未来的发展趋势[4−5]。使用Kalman滤波进行GNSS/INS组合解算时，需要精确确定过程噪声参数，特别是在高精度应用领域。常规做法是采用Allan方差方法[6−8]提取所需的噪声，由于该方法本身含有误差，使用直线拟合获取噪声参数时也存在拟合误差，需将提取到的参数再进行调整。然而，目前调节方案系人为主观调节，缺乏客观的评价指标。本文考虑到高铁轨道具有优良的刚性结构和极其规则的路线，设计实测实验让轨检小车对同一段轨道进行2次独立测量，通过对比轨检小车两次经过同一里程处检测出的偏差，来反映轨道不平顺性检测的重复性，通过该重复性对噪声参数的优劣进行评价。以Allan方差方法所得出的噪声参数为基础，反复调节相应参数，使得轨道检测重复性最高的参数即为惯导最优过程噪声参数。

1 利用Allan方差方法提取惯导过程噪声

1.1 Allan方差方法基本原理

Allan方差分析法是一种基于时域噪声分析法，它不仅能够识别噪声类型，还能确定噪声的特性参数，广泛应用于各种噪声分析。

Allan方差反映了相邻2个采样段内的平均频率差的起伏。若对长度为，采样时间为0的数据按平均因子进行分组，记第组的平均值为Y()，其中=0为相关时间，则Allan方差表示如下：

画出Allan标准差与相关时间的双对数曲线，可依据曲线斜率分辨出各噪声的类型和随机特性，IEEE标准协会给出的典型的陀螺和加速度计原始输出的Allan标准差图像斜率与各随机噪声类型如图1所示。

不同噪声项通常表现在不同的相关时间区间内，且双对数曲线的对应的斜率也各不相同。以陀螺为例，图1中曲线的最低点反映了陀螺零偏不稳定性，斜率为−1/2的直线段对应陀螺偏差白噪声(也称角度随机游走)，斜率为1/2的曲线段可以表征速率随机游走噪声[7]。斜率为正负1/2的两类噪声对过程噪声参数中的陀螺偏差与姿态随机游走的设置极为重要，其Allan方差与相关时间的表达式分别为：

式中：和分别为角度随机游走和速率随机游走的噪声系数；为相关时间。

粗略的Allan方差方法的误差相对百分比和相关时间关系如下：

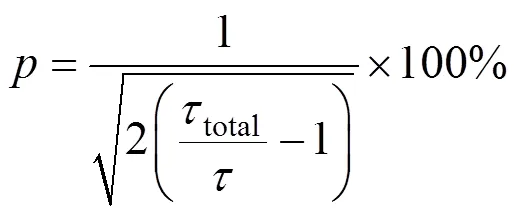
1.2 过程噪声提取

应用于轨道检测领域的惯导具有很高精度，本实验使用的设备为导航级激光惯导，将其静止放置预热2 h后，连续采集约4 h静止数据，对其进行Allan方差分析，得到的结果如图2和图3。从图2可看出，3个轴向的陀螺零偏不稳定性均接近甚至小于10−6deg/s，属于高精度导航级IMU。

对Allan方差结果分别使用斜率为−1/2和1/2的直线进行拟合，根据式(2)和(3)，当τ分别取1 s和3 s时，拟合直线对应的Allan标准差即为角度(速度)随机游走和速率随机游走噪声系数，结果如表1和表2所示。

图2 陀螺Allan方差结果

图3 加速度计Allan方差结果

表1 Allan方法提取出的陀螺过程噪声参数

表2 Allan方法提取出的加计过程噪声参数

2 轨道不平顺检测中最优过程噪声参数确定

搭载有GNSS/INS组合导航设备的T型轨检小车在由人力或动力车在铁轨上推行，采集到的原始观测数据使用松组合滤波进行解算，再通过RTS(Rauch–Tung–Striebel)平滑器[9−11]，解算出所测轨道的空间坐标序列，以此重构出三维铁路轨道。具体实测的铁路轨道和设计路线信息进行对比，便可获得各里程处的轨向偏差信息。需要指出的是，整段实测轨道应进行分割以适应不同实际线型的轨道偏差计算，具体方法可参考文献[12]和[13]。轨道检测对偏差的精度的要求极高，一般在毫米级。Allan方差方法提取噪声的过程中，所提取段的噪声易受相邻段噪声的污染，导致该段的斜率和理论斜率有一定偏移[14]，此外，直线拟合的过程中也会存在误差，因此由该方法确定出的噪声略显粗糙。使用Kalman滤波进行GNSS/INS组合解算时，需要精确确定过程噪声参数，因而需要将Allan方法确定的方差进行调整才能作为最终参数。

在实际轨道检测应用中，铁路轨道尤其是高速铁路轨道具有良好的刚性结构，而轨检小车的特殊设计也使其不易偏离轨道：小车本身具有一定重量，由于重力作用，在限定运行速度下不会发生高程方向上的跳跃；推行过程中T型梁内部弹簧使得车轮紧贴铁轨，从而不发生侧向的偏移。因此，当小车重复经过铁轨同一里程位置时，在算法精度很高的情况下，探测出的轨道不平顺结果应具有很高的一致性，且在其他条件不变的情况下，过程噪声设置越合理，一致性越好。因此，本文设计相应实验并在真实高铁轨道上进行验证，通过让轨检小车2次独立测量同一段轨道，通过重复性分析来评价方差设置的合理性，并以此搜寻出最优过程噪声参数。具体步骤如下：

1) 利用Allan方差方法确定噪声参数，将其作为配置参数输入组合算法中，分别解算出两趟独立测量的轨向偏差；

2) 对2次测量中同一里程处的偏差做差比较，并计算差值序列的STD值；

3) 微调表2和表3某种参数(例如，轴加速度计偏差)的过程噪声谱密度配置，重新进行偏差解算并记录相应差值的STD值；

4) 重复步骤(3)直至找出最小的STD值并记录对应的过程噪声参数，固定该参数；

5) 调整下一个过程参数直至搜寻出使得上述STD值最小的全套惯导过程噪声配置。

按照上述方案对Allan方差方法确定的过程噪声调整如表3，表4和图4所示。

表3 根据重复性准则确定的最优陀螺过程噪声参数

表4 根据重复性准则确定的最优加计过程噪声参数

图4 改变X轴各个过程噪声参数对轨向偏差重复性的影响

获取最优参数配置后，在最优参数附近按比例改变陀螺和加速度计(以轴为例，轴和轴以此类推)各个参数的大小，计算出2趟轨向偏差差值的STD值如图4所示。从图4可以看出，轨道不平顺结果的重复性对IMU器件的角度随机游走的敏感显著大于速率随机游走，实际参数调整过程中应十分注意。此外，对比表1，表2和表3，表4，Allan方差陀螺和加速度计的角度随机游走的与最优配置相差不大(不超过40%)，而速率随机游走相差较远(最大约为400%)，原因：

1) 从图1可以看出，角度随机游走的相关时间小于速率随机误差，根据式(4)，其估计精度较低；

2) 从图2和图3可以看出，静态采样时间有限，表征速率随机游走的数据簇(斜率为1/2曲线段)过少，造成拟合误差过大，特别是陀螺，其1/2斜率段数据更少，因而与加速度计相比，其Allan方差结果与最优配置相差更远，加速度计速率随机游走最大相差约1倍，而陀螺速率随机游走相差约4倍。而幸运的是，轨道不平顺结果对IMU器件的速率随机游走的敏感度相对不大，Allan方差方法结果依旧较为可靠。

3 最优配置与Allan方差方法轨道不平顺性对比

为了检验本文所提出方案的正确性，在真实高铁轨道上设计了相关实验进行验证。实验路段为桂柳线一段长约为3 km的轨道，轨道线型包含直线、缓和曲线和圆曲线。如图5所示，其轨向30 m波长不平顺测量结果均在2 mm以内，未超过规范[1]中规定的限差，说明该轨道目前运营正常。

图5 轨向30 m波长不平顺

为了直观描述最优过程噪声配置方法的改进效果，图6和图7分别给出了由2种配置方法计算出的实测高铁轨向偏差，表5比较了2种方法的偏差重复性，列出了2个测回分别测量出的轨向偏差的差值的统计数据。可以看出，最优配置方法的偏差重复性明显好于Allan方差方法，测量出的2趟偏差在幅值和走势上均符合的很好，而Allan方法的重复性不够稳定，仅在某些路段符合相对较好(例如里程1 000 m附近)，而在其他路段则相对较差。最优配置方法的重复性的均值、STD值和最大值为(0.05，0.39，1.04) mm，相比Allan方法提升了(90%，89%，83%)。

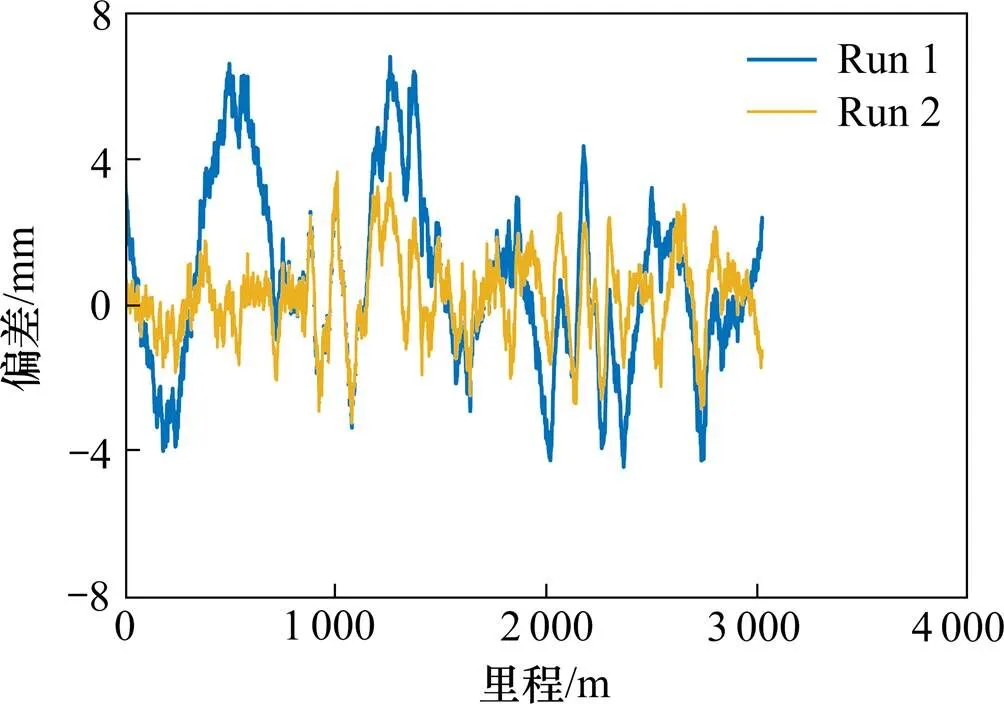
图6 Allan方法配置过程噪声计算的2趟轨向偏差

图7 最优方法配置过程噪声计算出的2趟轨向偏差

表5 Allan方差方法与最优配置的轨向偏差重复性比较

4 结论

1) 轨道不平顺对IMU器件的角度随机游走的敏感度显著大于速率随机游走，实际调参操作中应当注意。

2) Allan方差方法提取过程噪声的较为可靠，尤其是角度随机游走，与最优方差配置不超过40%。

3) 最优配置与Allan方差方法计算的轨向偏差重复性对比表明，调整后的结果有很大改善，其中互差标准差减小了89%。

[1] TB10601——2009, 高速铁路工程测量规范[S]. TB10601——2009, Specifications for survey engineering of high-speed railway[S].

[2] İŞahin. Railway traffic control and train scheduling based on inter-train conflict management[J]. Transportation Research Part B Methodological, 1999, 33(7):511–534.

[3] Groves P D. Principles of GNSS, inertial, and multisensor integrated navigation systems[M]. Boston: Artech House, 2014: 90−92.

[4] Glaus, R. Kinematic track surveying by means of a multi-sensor platform[D]. Switzerland: Swiss Federal Institute of Technology Zurich, 2006.

[5] CHEN Q, NIU X, ZUO L, et al. A railway track geometry measuring trolley system based on aided INS[J]. Sensors, 2018, 18(2): 538.

[6] 高宗余, 方建军, 于丽杰. MEMS传感器随机误差Allan方差分析[J]. 仪器仪表学报, 2011, 32(12): 2863−2868. GAO Zongyu, FANG Jianjun, YU Lijie. Allan variance analysis for the stochastic error of MEMS sensors[J]. Chinese Journal of Scientific Instrument, 2011, 32(12): 2863−2868.

[7] 刘建锋, 丁传红, 王医民. 基于Allan方差的激光陀螺信号分析[J]. 仪器仪表学报, 2007(增1): 113−115, 141. LIU Jianfeng, DING Chuanhong, WANG Yimin. Analysis of laser gyroscope signal based on Allan variance[J]. Chinese Journal of Scientific Instrument, 2007(Suppl 1): 113−115, 141.

[8] El-Sheimy N, HOU H, NIU X. Analysis and modeling of inertial sensors using Allan variance[J]. IEEE Transactions on Instrumentation & Measurement, 2007, 57(1): 140−149.

[9] Gelb A. Applied optimal estimation[M]. Cambridge: The MIT Press, 1974: 157−173.

[10] ZHANG X, ZHU F, TAO X, et al. New optimal smoothing scheme for improving relative and absolute accuracy of tightly coupled GNSS/SINS integration[J]. GPS Solutions, 2017, 21(3): 861−872.

[11] GAO Z, GE M, LI Y, et al. Railway irregularity measuring using Rauch-Tung-Striebel smoothed multi‑sensors fusion system: Quad‑GNSS PPP, IMU, odometer, and track gauge[J]. GPS Solutions, 2018, 22(2): 36.

[12] Gikas V, Stratakos J. A novel geodetic engineering method for accurate and automated road/railway centerline geometry extraction based on the bearing diagram and fractal behavior[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(1): 115−126.

[13] 李姗姗, 陈起金, 旷俭, 等. 铁路轨道线形智能分段[J]. 科学技术与工程, 2016, 16(34): 276−279. LI Shanshan, CHEN Qijin, KUANG Jian, et al. Linear segmentation of railroad track lines[J]. Science Technology and Engineering, 2016, 16(34): 276−279.

[14] NIU X, CHEN Q, ZHANG Q, et al. Using Allan variance to analyze the error characteristics of GNSS positioning [J]. GPS Solutions, 2014, 18(2): 231−242.

Determination of optimal process noise parameters of INS and its application in high-speed railway track irregularity measuring

ZHOU Wuxing, ZHU Feng, ZHANG Xiaohong

(School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China)

Track irregularity measuring technique based on high precision GNSS/INS integration need to determine the process noise parameters precisely, so as to accomplish the optimal data fusion. The noise parameters extracted by using conventional Allan variance method was pretty rough. Considering the rigid structure of steel rails and the special design of the track inspection trolley, the repeatability of track deviation at the same mileage point where the trolley passes twice during two independent surveying missions serves as an evaluation index and the optimal process noise parameters was obtained further based on those from Allan variance method. The field data shows that the track irregularity is much more sensible to IMU angular random walk than rate random walk, and the angular random walk parameters extracted by Allan variance method is quite accurate, with an error less than 40% compared to the optimal configuration. Moreover, the repeatability performance is improved remarkably after the adjustment of the parameters, with the STD value of the mutual difference decreasing by 89%. In conclusion, the approach presented in this paper could benefit GNSS/INS-based track irregularity measuring operation to a great extent.

track irregularity measuring; GNSS/INS integration; Allan variance; deviation repeatability; parameter adjustment

U216.3

A

1672 − 7029(2019)09− 2137 − 06

10.19713/j.cnki.43−1423/u.2019.09.001

2018−11−20

国家杰出青年科学基金资助项目(41825009)；创新研究群体科学基金资助项目(41721003)

朱锋(1989−)，男，浙江绍兴人，博士，从事多源组合导航与精密工程测量研究；E−mail：fzhu@whu.edu.cn

(编辑 蒋学东)