大角度单摆微扰解的分析
洪海莲,马 豪, 颜慧贤,林俊武,王宗篪
(三明学院 机电工程学院,福建 三明 365004)
单摆是一种重要的物理模型,但是在大学物理教学中,只考虑理想的单摆模型,即摆动角,这是因为当单摆做小角度摆动时,存在的近似,此时单摆运动的微分方程可以认为是线性方程,单摆做简谐振动,可求得单摆的精确解。在实际应用中,摆动角在很多情况下,如果仍然套用线性方程的公式进行计算,误差很大,同时也不利于学生对大角度摆角问题的理解。
目前,研究大角度摆角问题的方法主要有相平面法、线性内插法、叠代法等,上述方法基本都是将大角度时的非线性方程转化为易于处理的新变量非线性方程,再用较为复杂的贝塞尔函数或者椭圆函数来构成方程的逼近解,这些方法确定的解析解的逼近精度不高,同时,对这些复杂解的理解仍然存在很大困难。
本文首先应用泰勒级数展开,用微扰法分析非线性方程,求出周期、圆频率和振动的表达式,结果表明大角度摆角的振动为基波与三次谐波的叠加。再用数据可视化极高的Matlab软件,模拟非线性方程的微扰解,同时与理想单摆模型的精确解进行比较,得出误差,从而用更加简化、直观的方式满足学生对大角度单摆理论的理解。
1 大角度单摆微扰解的确定
设摆球的质量为m,摆线的质量忽略,其长度为l,由牛顿第二定律可以计算出单摆的微分方程为:
(1)
一般认为在摆动角很小的情况下,θ≤5°,存在θ≈sinθ,此时公式(1)简化为:
(2)

但是超过这个摆动角的范围,即θ>5,θ≈sinθ近似不成立,两者之间存在较大误差,非线性方程(1)的解很难求出。采用微扰法可以给出该方程的形式解,首先将做级数展开,如下:

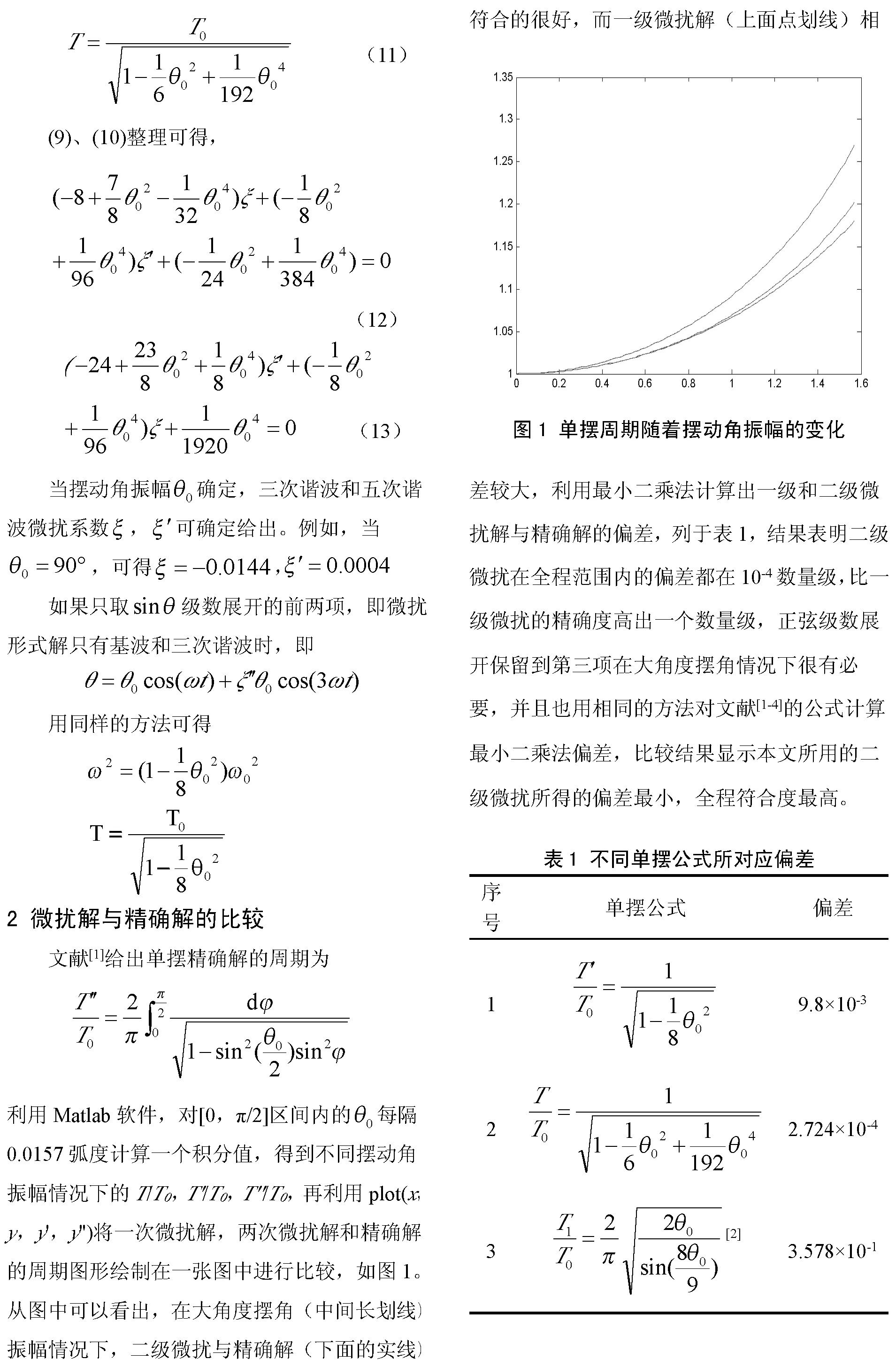

同时,再画出公式(12)、(13)在摆动角振幅不同情况下的三次谐波和五次谐波系数ξ,ξ'如图2
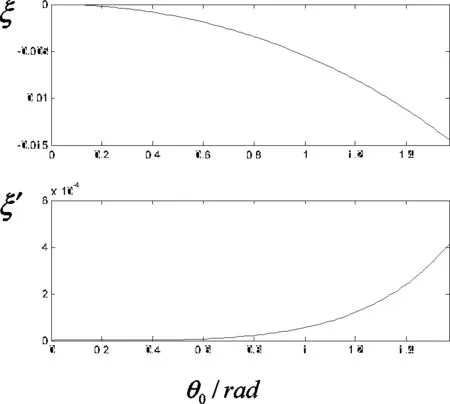
图2 单摆三次谐波和五次谐波微扰
由图可以看出,三次谐波的系数为负值,这与正弦泰勒级数展开项前为负号一致,其取值范围在10-2~10-3之间,而五次谐波的系数为正值,这与正弦泰勒级数展开项前为正号一致,其取值范围在10-4数量级,可见,高次谐波贡献较小,在大角度摆角范围,三次谐波是基波强度的1/100倍,五次谐波是三次谐波的1/100倍,并且在范围内ξ'几乎为零,这意味着摆动角在区间,形式解展开到三次谐波范围精确度已经很高,并且在内,ξ几乎为零,这表明在小角度范围内,,单摆可以看成是简谐振动,单摆运动方程的解只包括基波余弦项,不存在高次谐波项。
3 结论
本文引入微扰方法,推导了单摆的微扰形式解,目的在于将单摆非线性方程简化,得到简单易于理解的结果,避免了对椭圆积分复杂解的解析,利于对单摆问题的理解。本文同时利用计算功能Matlab软件,对单摆振动周期的精确解和各级微扰解用曲线形式进行比较,并用最小二乘法对各级微扰进行误差分析,起到更为直观、简便理解单摆周期变化的效果,同时,也用Matlab软件画出任意摆角情况下的微扰系数曲线,并根据作图结果逐一分析五次谐波、三次谐波基于摆角大小的选取情况,加深对各级微扰系数的理解。本文在精度极高的前提下给出的微扰单摆公式简洁、物理意义明确,进一步充实了对大角度单摆的理解。

