基于OPA-环形腔光力学系统的纠缠特性研究

王 婧

(通化师范学院 物理学院，吉林 通化134000；吉林大学 物理系，长春 130012)

腔光力学系统一般由光学腔或微波腔与可移动镜子组成。当一束泵浦光从部分透射的腔镜入射后驱动腔中光模，并对可移动镜子产生光辐射压力，从而实现腔中光场与可移动镜子之间发生动态的光力相互作用。腔光力学系统在理论和实验上都做了大量的研究工作[1-5]。例如，可移动镜子和固定腔镜之间的纠缠[6-7]、双稳和多稳[8]、光力诱导透明OMIT (Optomechanically Induced Transparency)[9-10]、本征模劈裂[11]等。

本论文以文献[12]中的物理模型为基础，在其中加入光学参量放大器OPA(optical parametric amplifier)，研究OPA-环形腔光力学系统中的纠缠动力学特性。具体的物理模型是一个包含光学参量放大器OPA在内的由两个可移动的全反射镜子和一个固定部分透射的腔镜构成的环形腔光力学系统。

1 理论模型与主要公式

图1 系统原理图

在旋转坐标系下，整个系统的总哈密顿量表示为:

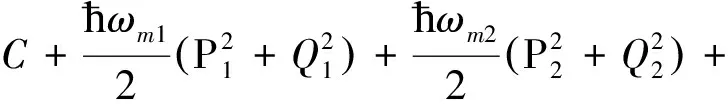
(1)

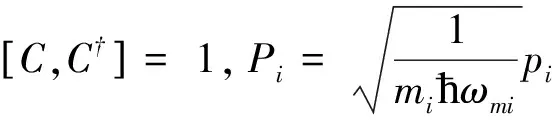
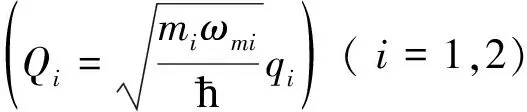
在考虑相关的噪声来源和衰减后，由系统哈密顿量(1)式可以得出算符Pi、Qii=1,2、C的量子郎之万运动方程在海森堡表象下为:

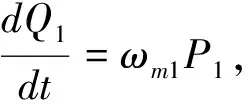
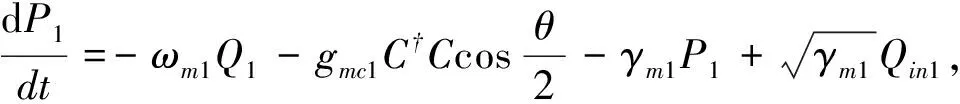
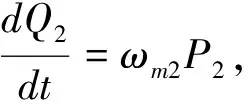
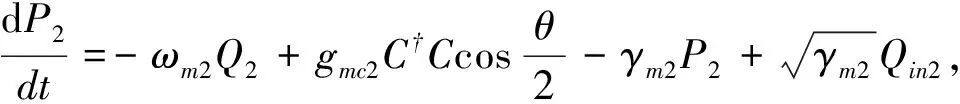
(2)

其中，Qinjj=1,2表示作用在可移动镜子上的热噪声，Cin表示的是腔镜的输入量子真空噪声算符。

当δB≪Bs(B=P1,P2,Q1,Q2,C)时，方程(2)中的每个算符都改写为稳态解加上其涨落算符的形式：B=Bs+δB()。将改写后的算符代入方程(2)，从而分离出两组方程。其中一组为系统的稳态解:

Psi=0,

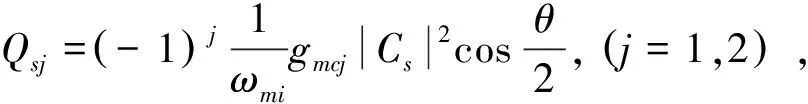
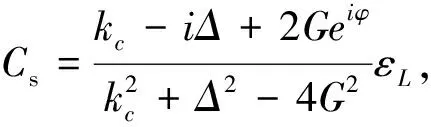
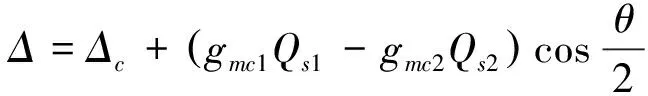
忽略非线性项δC†δC和δCδQii=1,2，得到另一组关于系统的涨落算符的方程:

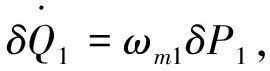
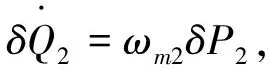
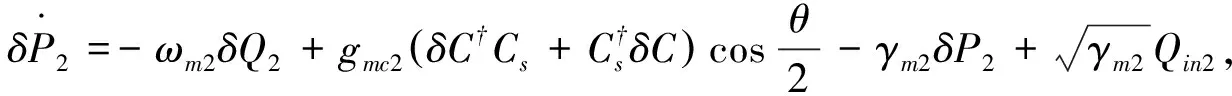
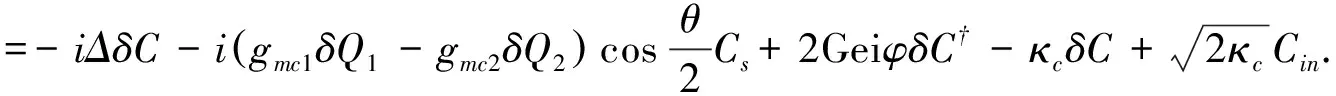
(3)

(4)

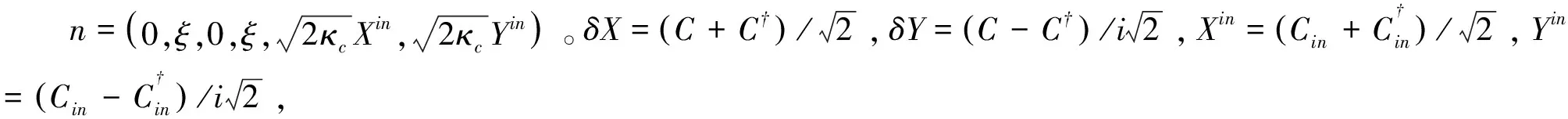
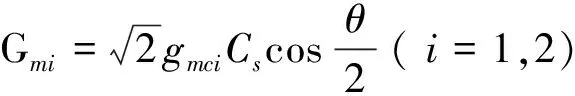
当系统的稳定条件被满足时，关联函数满足李雅普诺夫方程AV+VAT=-D。关联矩阵V可以写成块矩阵的形式。

对数负值定义为:

EN=max[0,ln(2η-)]，

其中，η-=2-1/2σ-σ2-4detVs1/21/2,σ=detVm+detVC-2detVmC。当EN>0时，会发生宏观纠缠。

2 分析与讨论

2.1 非线性增益参量G值对腔场和可移动镜子1纠缠的影响

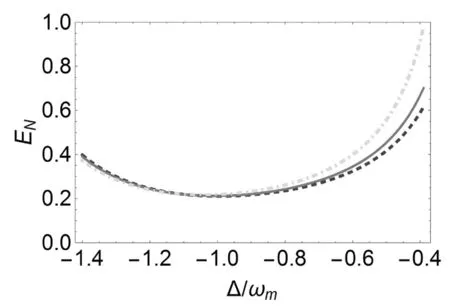
图2 非线性增益参量G值对腔场和可移动镜子1之间纠缠的影响。 G=0，G=1×107Hz，G=3×107Hz。

2.2 驱动光学参数放大器相位对腔场和可移动镜子1之间纠缠的影响

图3是驱动光学参量放大器相位φ对腔场和可移动镜子1之间纠缠对数负值的影响。其中φ=0，φ=π/4，φ=π/2。从图3中可以看出来，当Δ<-ωm时，腔场和可移动镜子1之间纠缠随着驱动光学参数放大器相位φ的增大而减少。当Δ>-ωm时，腔场和可移动镜子纠缠随着驱动相位φ的增大而增大。纠缠对数负值曲线相交于Δ=-ωm点。这使得腔场与可移动镜子1之间的耦合是分束器型的相互作用[14]。

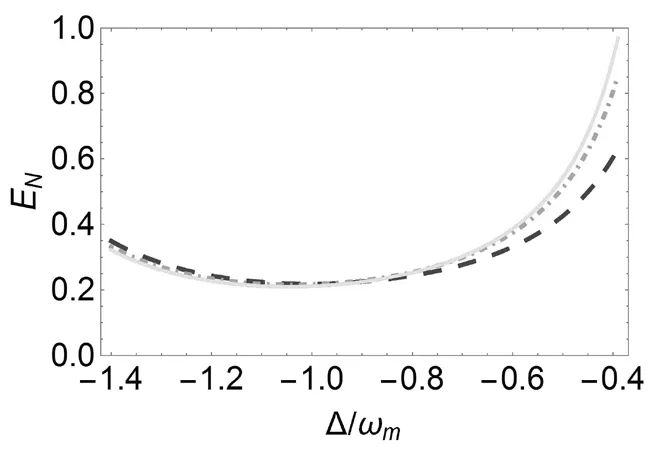
图3 驱动光学参数放大器相位对腔场和可移动镜子1之间纠缠的影响。φ=0，φ=π/4，φ=π/2。

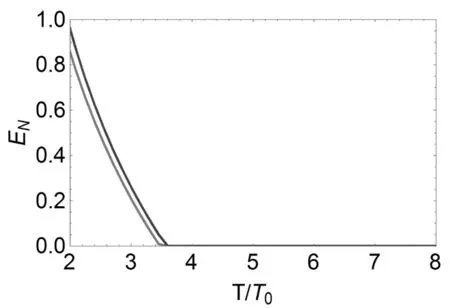
图4 腔场和可移动镜子纠缠随环境温度的变化关系趋势图。G=9×107Hz，G=0×107。

2.3 腔场和可移动镜子纠缠随热库温度的变化

在图4中，我们研究腔场和可移动镜子1之间纠缠随环境温度变化的情况。从图4中可以发现，当G=9×107Hz时，随着环境温度的逐渐升高，腔场和可移动镜子1之间纠缠强度逐步减少。同时，当环境温度高于T>7.2mK时,腔场和可移动镜子1之间的纠缠会消失。这是因为环境温度越高，导致热库噪声越强，破坏了腔场和可移动镜子1之间的纠缠行为越强。对比图中两条线，腔场和可移动镜子1之间纠缠行为随着增益G增加而增强。纠缠最大值从0.84变到0.96，纠缠消失点的温度也有所提高。