低温高应力下水工沥青混凝土粘弹特性实验研究
叶 永 杨佳奇 牟玉池 郑保敬
(三峡大学 水利与环境学院,湖北 宜昌 443002)
水工沥青混凝土是一种复合材料,具有耐久性、不透水性和柔韧性的优点,它广泛应用于水工建筑物的防渗系统中[1-2].目前沥青混凝土的科研成果大部分集中在道路工程中.水工沥青混凝土的研究成果应用相对不足,特别是在低温高应力情况时的力学性能分析更少[3].本文研究了沥青混凝土在低温高应力状态下的蠕变行为,研究了不同加载温度和不同加载应力下水工沥青混凝土的力学性能.利用4种常用的蠕变本构模型展示其粘弹特性,比较分析每种模型的优缺点,得到在低温高应力条件下能反映水工沥青混凝土特性的最优本构模型.通过与实验数据拟合,得到最优模型在不同温度和加载应力条件下的模型参数,并研究不同实验条件下各参数的变化规律.研究结果为水工沥青混凝土的工程应用提供理论依据和计算参数.
1 蠕变实验
1.1 实验材料
1)沥青:AH50沥青主要技术指标:针入度53(0.1 mm)、软化点54.3℃、延展性164cm(15℃).
2)骨料:粗骨料使用玄武岩,主要检测指标有表观密度2722 kg/m3、吸水率0.81%、针片状颗粒含量5.4%、黏附性5.2级;细骨料使用表面洁净、颗粒圆润河沙,其检测指标是吸水率1.7%、水稳定性等级8级.
3)填料:采用粒径小于0.075 mm的碱性矿粉水泥作为填料,主要技术参数指标为表观密度3 223 kg/m3、含水率0.16%、亲水系数0.9%.实验所用级配指数是0.4,其相关配合比见表1.

表1 水工沥青混凝土配合比
1.2 实验设计
根据DL/T 5362-2006《水工沥青混凝土试验规程》,按照最佳沥青含量成型Marshall标准试块,试件尺寸101.6 mm×87 mm(直径×高度),所有实验在万能试验机上进行.万能试验机配有温度箱,箱里温度由液氮加热器来控制和实现.实验开始时,将试件置入环境温度箱里,打开液氮加热器开关,让箱内温度降至设计温度并达到稳定.为保证试件内部温度达到实验设计温度,试件在温度箱里降温时间不能低于2 h.
根据作者前期工作[4-5],确定低温和高应力范围,设计如下方案.方案1:在6 MPa加载应力条件下,改变实验温度,分别为-10℃、-5℃、0℃、5℃、10℃.方案2:在实验温度0℃情况下,改变加载应力,分别为3 MPa、4 MPa、6 MPa、8 MPa.为消除人工误差,在实验前,首先对试件采取预先加载措施,其应力是0.01 MPa,时间是2 min,然后再以20 mm/min速度将应力增长到设计值.每组实验进行3次,平均3次作为该组实验结果.蠕变时间取1 200 s.
1.3 实验结果
图1表示了加载应力是6 MPa,不同温度对应的蠕变曲线.
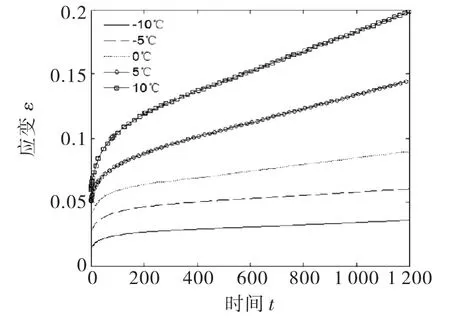
图1 不同温度下蠕变曲线(6 MPa)
由图1可以看出,在同一温度条件下,水工沥青混凝土的应变都随着时间的增加而增大,实验开始时应变增加较快,随后趋向于匀速增加(从曲线斜率得到),曲线也反映了水工沥青混凝土的减速和等速两个蠕变过程,其中,第一过程为瞬时弹性变形,第二过程为粘性流动变形[5].当温度不同时,随温度升高,相同时刻应变值会变大,应变速率也变大,实验曲线反映了材料的温度效应.
图2表示同一温度(0℃)但应力不同情况时的实验曲线.由图2可以看出,低温情况时,同一应力作用下,水工沥青混凝土应变均随着时间增加而增大,实验曲线也清楚地反映了水工沥青混凝土减速和等速蠕变2个不同过程.在不同应力作用下,随加载应力增大,同一时刻应变值越大,应变速率也越大,实验曲线反映了材料明显的应力变形特点.图1和图2结合时间效应来看,水工沥青混凝土材料表现了很好的粘弹特性[6].

图2 不同加载应力下蠕变曲线(0℃)
2 常用粘弹性本构模型
对材料粘弹特性本构关系的描述可采用弹性和粘性的物理模型进行,通过相应元件采取串并联组合的方式来构造粘弹性模型[4].
1)Zener模型:由单个Kelvin模型加上单个弹性构件组合,也称三参数固体模型,具有瞬时弹性及稳态渐进性,能够显示出固体材料特征.其蠕变方程为:
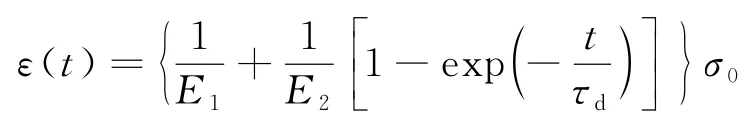
2)三参数流体模型:由单个Kelvin模型加上单个粘性元素组合.其蠕变方程为:

3)Burgers模型:又称为四参数流体模型,由单个Maxwell模型和单个Kelvin模型串联组合,其应变随时间延长近似线性增大,该模型也表现出流体的特征.其蠕变方程为:
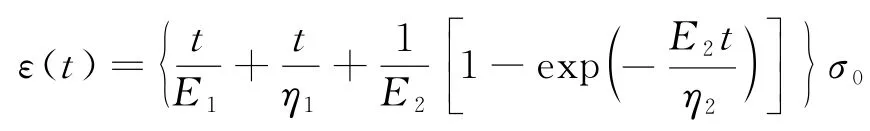
4)四参数固体模型:与以上3种不同,通过2个相同的Kelvin模型串联在一起构成.其蠕变方程为:

3 模型对比分析
利用最小二乘法原理编写了非线性拟合程序,将以上4种蠕变本构模型和试验数据进行拟合,得到各模型在同一温度不同加载应力和同一加载应力不同温度条件下的模型参数及相关系数,通过对比分析,找出最适合和最能够反映水工沥青混凝土处于低温高应力情况时蠕变过程的本构模型.
图3是加载温度-10℃、加载应力8 MPa时,4种本构模型与实验结果的拟合曲线.在起始点,Zener以及Burgers模型均能较好拟合.三参数流体模型以及四参数固体模型的蠕变起始点应变值相同,均是0,可见这两种都不能够拟合实验的起始蠕变应变.在等速蠕变阶段,Zener模型拟合曲线应变值在900 s前要大于实验值,900 s后小于实验值,而Burgers模型拟合曲线在等速变阶段和实验曲线较为接近,虽然加载时间在800 s前拟合曲线应变值比实验曲线略小一些,800 s后略大于实验曲线应变值,但总体偏差较小.由此可见,Burgers模型更能够反映水工沥青混凝土在-10℃和8 MPa应力条件下的蠕变特性.
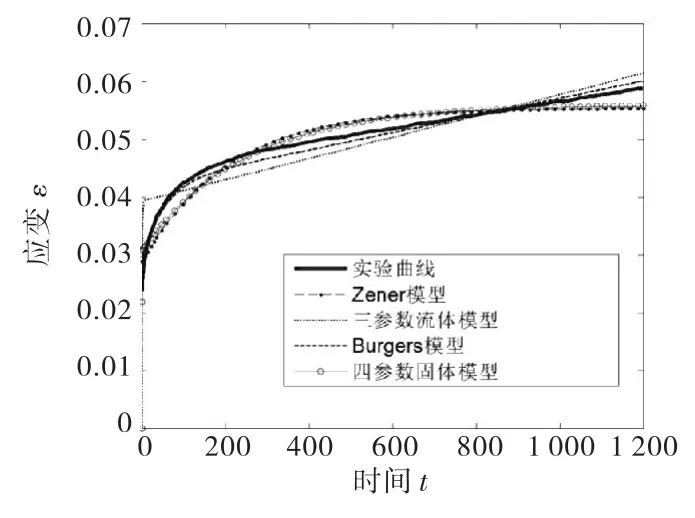
图3 温度为-10℃、应力为8 MPa时的模型对比
表2为水工沥青混凝土在-10℃时,加载应力为4 MPa、6 MPa、8 MPa的相关参数;表3为水工沥青混凝土在加载应力为4 MPa,加载温度为-10℃、-5℃、0℃、5℃、10℃时的相关参数.可以发现,Burgers模型总体上相关系数最高,且模型起始蠕变更接近实验曲线,减速及等速蠕变的两个过程延续时间更接近实验曲线.
综上所述,Burgers模型和其他常用粘弹性模型相比,更能体现水工沥青混凝土在低温高应力情况时的蠕变特性.
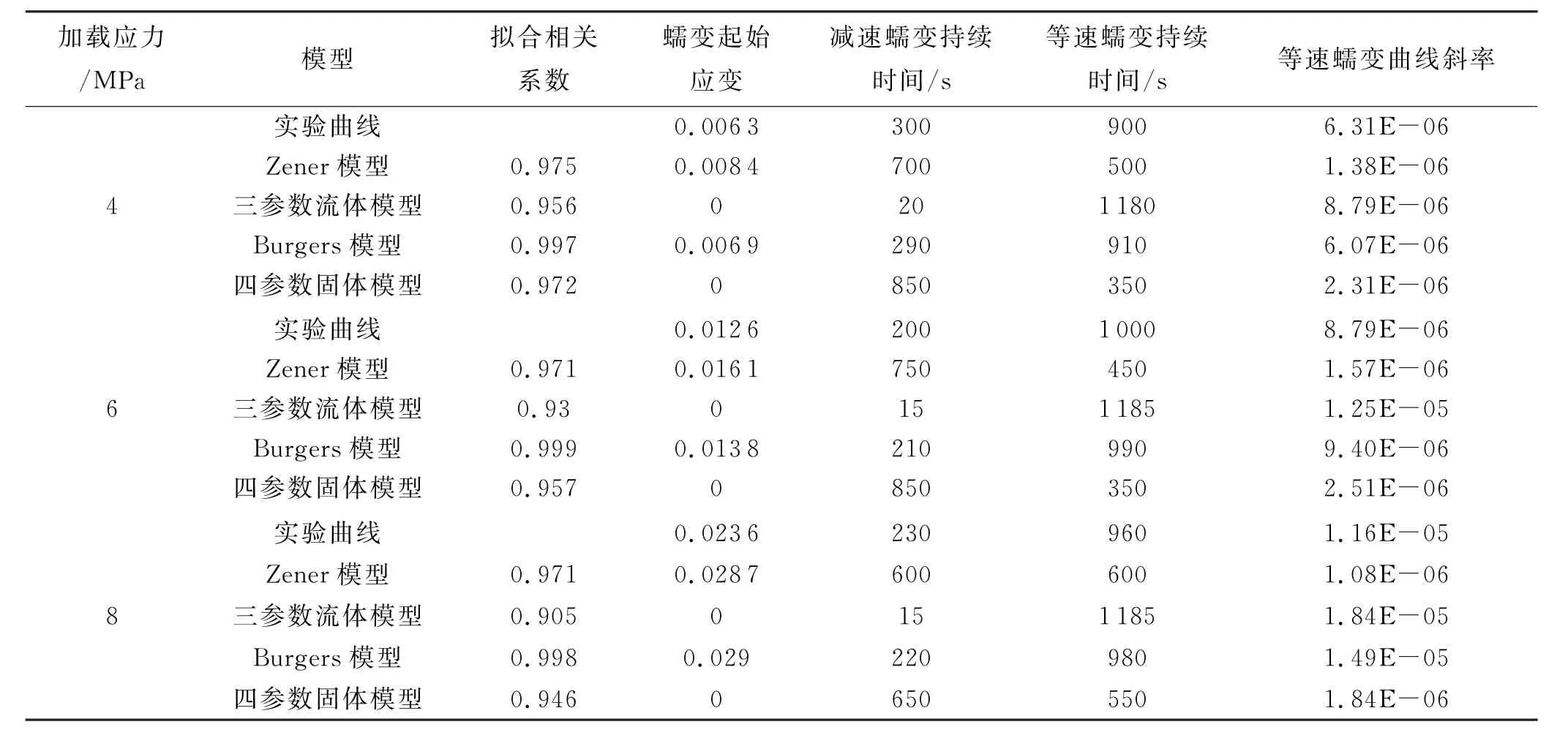
表2 -10℃拟合相关参数
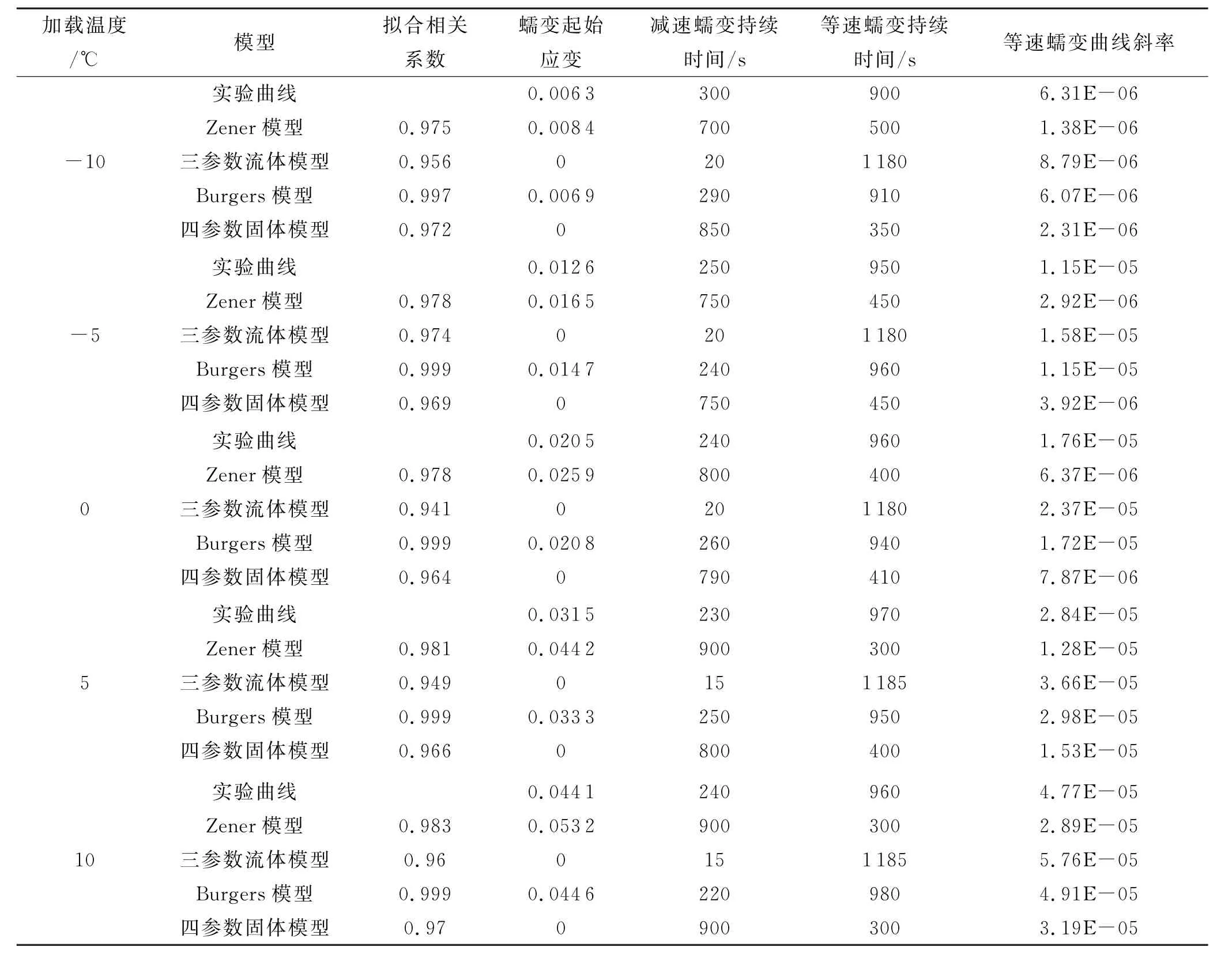
表3 4 MPa拟合相关参数
4 最优模型参数研究
研究Burgers模型参数随不同加载应力和实验温度的变化规律.图4、图5是模型参数E1、E2、η1、η2在相同温度(0℃)下,与加载应力3 MPa、4 MPa、6 MPa和8 MPa的关系.可知,在实验温度相同时,Burgers模型参数E1、η1随加载应力增大而减小,呈曲线分布,分布规律不明显,而模型参数E2、η2随着加载应力增大而增大,几乎呈线性分布,具有一定的规律性.
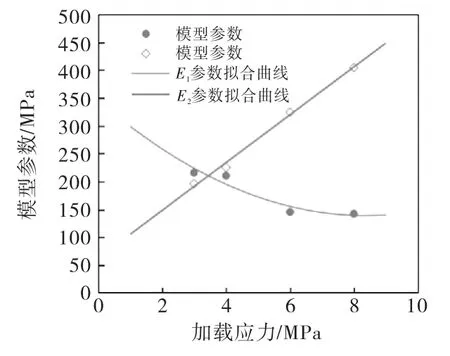
图4 模型参数E 1、E 2与应力关系

图5 模型参数η1、η2与应力关系
图6和图7是模型参数E1、E2、η1、η2在相同加载应力(4 MPa)下,与实验温度-10℃、-5℃、0℃、5℃、10℃的关系.可知,在同一加载应力条件下,Burgers模型参数E1、η1、E2、η2均随着温度升高而减小.当温度变化时,参数E2、η2同样具有更好的规律性.
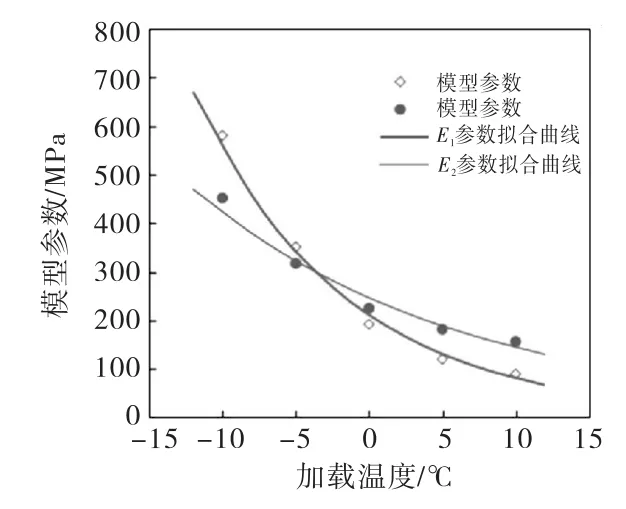
图6 模型参数E 1、E 2与温度关系
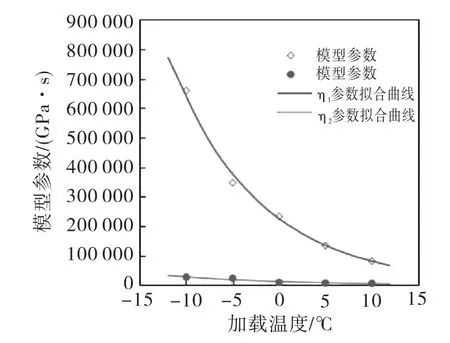
图7 模型参数η1、η2与温度关系
从模型参数与拟合曲线的离散程度来看,模型参数对不同温度条件的拟合相关性要优于不同应力条件,离散程度要低,这说明Burgers模型参数随温度变化具有更好的规律性以及对温度具有更大的依赖性和敏感性,这一点正是粘弹性材料具有更明显的温度效应特征的反应,而Burgers模型正好反映了这一特征.这一结果为Burgers模型在水工沥青混凝土低温高应力条件下的工程应用提供了模型选择依据.
5 结 论
进行了沥青混凝土在温度-10℃、-5℃、0℃、5℃、10℃,加载应力3 MPa、4 MPa、6 MPa、8 MPa条件下的蠕变实验,并利用4种常用本构模型进行材料粘弹性分析,得到以下结论:
1)水工沥青混凝土在低温、高应力作用时的蠕变可分为两个过程,也就是减速蠕变过程以及等速蠕变过程.在温度固定时,加载应力越大,起始蠕变点应变随之变大,同一时刻对应应变也就越大;在加载应力固定时,温度增高,起始点应变增大,同一时刻对应应变增大.材料变形随应力和温度的变化,以及时间效应正是粘弹性材料的固有特征.
2)4种常用模型比较,Burgers模型起始应变更接近实验曲线,也能够反映水工沥青混凝土减速及等速蠕变两个阶段的特点.结合相关系数大小,Burgers模型能够更好反映水工沥青混凝土在低温高应力时的蠕变特征,是最优的粘弹性模型.
3)在不同实验温度下,Burgers模型弹性系数E1,E2和粘度系数η1,η2随着温度的升高而降低.在不同应力条件下,弹性系数E1和粘度系数η1随应力的增加而减小,弹性模量E2和粘度系数η2都随应力的增加而增加.应力和温度相比而言,模型参数对温度变化表现更好的相关性,反映了材料对温度变化有更强的敏感性和依赖性特征.

