鹤壁市城镇体系空间结构优化
李铭辉,窦富国,于 壮,张合兵,邵河顺
(1.河南理工大学测绘与国土信息工程学院,河南焦作 454000;2.河南省鹤壁市国土资源监察支队,河南鹤壁 458000)
城镇体系是指在一定地域范围内,以中心城市为核心,由一系列不同等级规模、不同职能分工、相互紧密联系的城镇组成的复合有机整体[1]。城镇体系在推进区域城镇化,促进资源合理利用、产业结构优化调整和社会经济快速协调可持续发展方面起着重要作用。城镇体系空间结构是区域发展的骨架,其特征是区域政治、经济、文化等因素长期发展演变,在地域空间上的综合表现,从理论上来讲,城镇体系空间结构不可能达到完全合理的状态,因此研究区域城镇体系空间结构特征,对于了解区域城镇体系经济发展特征,促进区域城镇体系功能和结构的优化,实现区域经济的可持续发展具有重大意义。目前,国内学者对于城镇体系的研究多集中在规模等级研究[2-4]、空间结构特征及其演变规律研究[5-8]、影响因素研究[9-11]、城镇体系系统同其他系统的耦合机制研究[12-14]等方面。在研究方法上,多基于分形理论构建研究模型,这是因为城镇体系是一种复杂的非线性系统,具有无标度性,不能用确切的单位去计量描述,其空间分布具有自相似性,无规律可循。而分形理论可以很好地揭示城镇体系的无标度性和自相似性,对于描述城镇体系空间结构的几何分布特征具有良好的效果。目前,基于分形理论的城镇体系空间结构研究多采用行政区几何中心进行测算[15-16],或者通过遥感技术(remote sensing,简称RS)获取研究区城镇边界几何中心进行测算[17-18],均存在对城镇分形中心把握不够准确的问题。本研究将基于年度土地利用变更调查数据,精准提取乡镇建设用地边界,确定其分形几何中心,并测算鹤壁市县(区)城镇聚集维数和鹤壁市关联维数,在此基础上通过场强模型识别县(区)中心城镇辐射影响范围,定量描述鹤壁市城镇体系空间结构分布特征,对优化鹤壁市城镇体系空间结构,促进鹤壁市经济协调可持续发展具有重大意义。
1 研究区概况与数据来源
1.1 研究区概况
鹤壁市位于河南省北部,太行山东麓与华北平原交界处(113°59′~114°46′E、35°26′~36°53′N),东西北与安阳市接壤,南与新乡市相邻,南北宽约67 km,东西长约69 km,总面积2 140.43 km2。全市辖3区(鹤山区、山城区、淇滨区)2县(浚县、淇县)。鹤壁市境内自然资源丰富,已探明30多种矿藏,属国家能源重化工基地和黄淮海平原农业综合开发区。自1957年建市以来,城市发展“缘矿而建”,随着煤炭资源的不断开采及消耗,鹤壁市主城区先后经历了3次历史变迁,形成了现在典型的资源型城市城镇体系空间结构,但也遗留下许多历史发展问题,如城区不聚集、土地利用集约化程度低、环境污染情况严重等,严重制约了鹤壁市社会经济的发展。
1.2 数据来源
本研究所采用的数据来源于鹤壁市国土资源局提供的2014年度土地利用变更调查数据库、鹤壁市土地利用总体规划数据库(2009—2020)和统计局提供的2015年鹤壁市统计年鉴。首先提取鹤壁市各个乡镇建设用地边界,并对1 hm2以下碎小图斑进行剔除,县(区)城镇边界采用鹤壁市土地利用总体规划(2009—2020)确定的县(区)中心城区;然后利用ArcGIS空间分析工具确定各个城镇建设用地几何中心,并计算得到各个城镇点之间的欧式距离。
2 城镇体系空间结构分形研究方法
2.1 空间聚集分析
假定城镇体系内各结构按照某种自相似规则围绕中心城镇呈凝聚态分布,且分形体在各个方向是均匀变化的,则可以通过几何测度关系确定以r为半径的圆形区域内的城镇数目N(r)[19],其与对应的半径存在一定的关系:

式中:D为空间聚集分维数;r为回旋半径;N(r)是以中心城市为圆心、r为半径的圆形区域内的城镇个数。目前上式经过证明成立[20]。为了消除半径r的单位不同带来的误差,定义平均半径R来代替r:

式中:Rs为平均半径;S为区域内城镇点数量;ri是从中心点到第i个点之间的距离。上述公式的值代表由S个城镇点组成聚集区域的平均半径。平均半径与城镇数量的分维关系有:

通过线性回归即可计算分形维数D,D的含义可以解释为城镇体系分布从中心城镇向四周的聚集衰减程度,通常计算得到D值应该在0~2之间。当D>2时,城镇体系内城镇的分布密度沿着中心城镇向四周的方向递增,城镇沿着半径方向均匀散开呈离散状态分布;当D=2时,各个城镇围绕着中心城镇呈均匀态分布,没有聚集特征;当D<2时,各个城镇的分布在空间上围绕着中心城镇表现出聚集态,城镇的分布密度沿着中心城镇向周边方向逐渐减少,且D越小,周围城镇聚集程度越高。
基于以上模型,本研究分别以鹤壁市县(区)中心城区为中心城镇,计算鹤壁市城镇体系聚集维数。分别提取县(区)中心城镇几何中心,通过ArcGIS分析工具计算其到其他28个城镇的欧式距离,然后通过公式(2)计算得到平均半径(表1),再对点(Rs,S)取双对数,用(ln-ln)图表示(图1),对其进行回归分析。
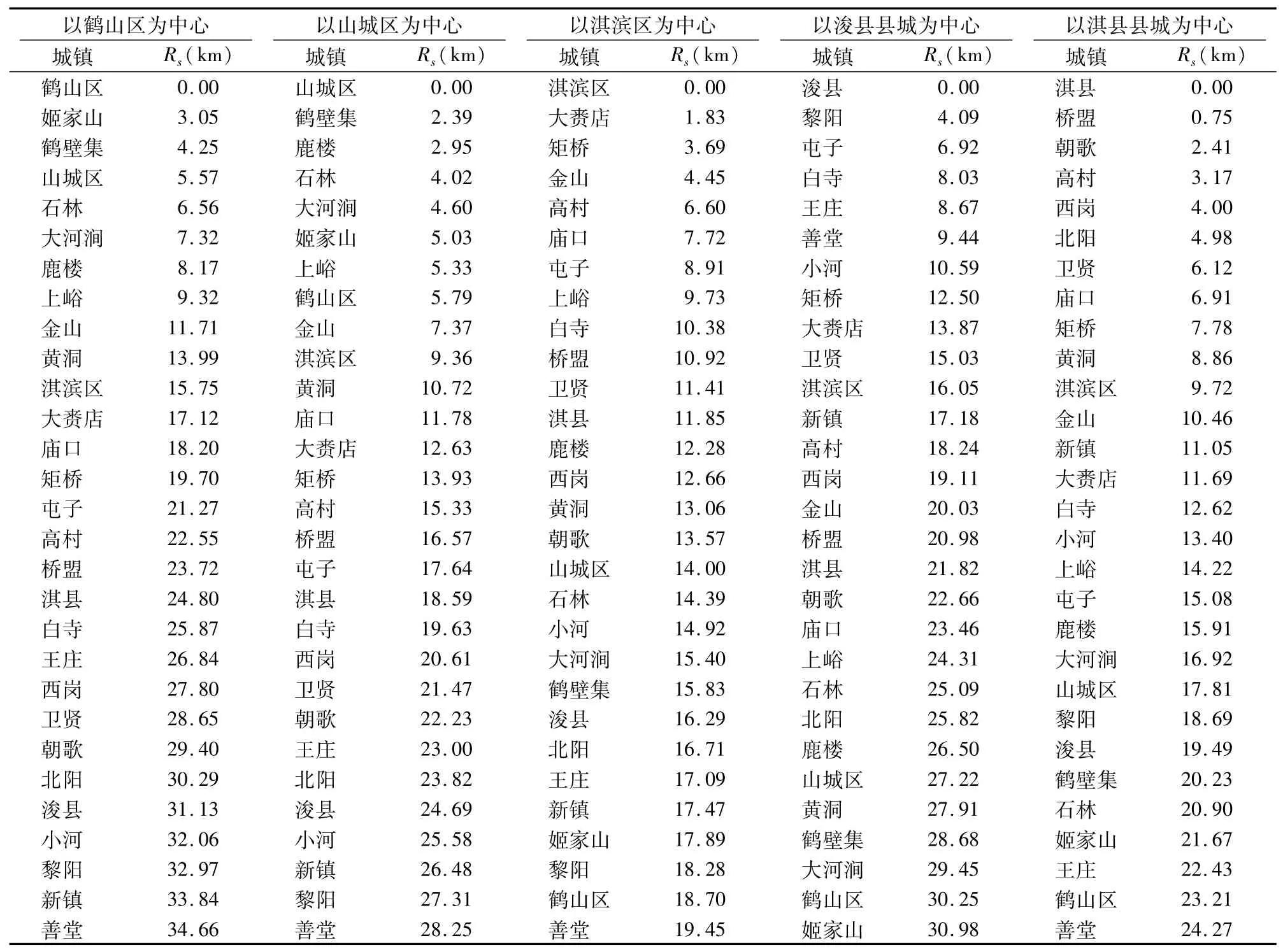
表1 鹤壁市城镇体系平均半径
2.2 空间关联分析
城镇体系空间结构的关联性分形通常采用空间关联维数进行研究。其模型为

式中:r为距离标度;C(r)为根据给定距离r所选取的城镇的数目;dij为城镇体系内第i个城镇与第j个城镇间的直线距离;H(r)为Heaviside阶跃函数。根据城镇体系空间分布的分形特征,有

式中:D为关联维数,其地理意义反映了城镇之间相互影响的规律性,为使计算方便,可令N(r)=C(r)N2,N(r)为dij≤r的城镇数目[17],那么式(6)可改写为:


通过线性回归可计算关联维数D,D值一般在0~2之间。当D取值趋近0,表明该地区内各个城镇之间关联紧密,空间相互作用强,各个城镇分布高度集中于某地;当取值D趋近1,表明各个城镇沿地理线集中分布,如河流、铁路、海岸等;当取值D趋近2,各个城镇之间关联不紧密,空间相互作用弱,城镇空间布局均匀且分散。
基于以上模型,以鹤壁市29个城镇为对象,计算整体关联维数。将29个城镇间两两欧式距离dij列成表格(表2),这实际上是一个对称矩阵,这里只列出半角,但计算城镇总点数时,必须考虑满阵的数据(即N2=29×29)。取标度r=55、50、45、40、35、…、5(步长Δr=5 km),对应的N(r)=841、821、…、51,于是得到点列[r,N(r)](表3),再对点列[r,N(r)]取对数,在坐标图中绘制,可以看出,点列呈线性分布(图2),并对其进行回归分析。
3 城镇体系中心城镇辐射范围识别研究方法
中心城镇作为区域城镇空间结构的核心,对周围城镇的发展具有不可替代的影响作用,其影响力与自身城镇规模成正比,与周围城镇距离成反比,并呈现距离衰减规律,最终与其他中心城镇之间的影响力达到平衡,在平衡处即为断裂点,断裂点处2个城镇之间的相互作用强度即为场强。
3.1 断裂点模型

式中:Di为城市i到断裂点的距离;Dij为i、j2个城市间距离;Mi、Mj为2个城市的综合规模指数,i代表起点城市,j代表终点城市。
3.2 场强模型

式中:Fik为城市i在断裂点k的场强大小;Dik为城市i到断裂点k的距离;Mi同上。
3.3 辐射半径模型

式中:Dr为城市i的辐射范围;F为所选择确定的边界场强;Mi同上。
3.4 中心城镇辐射范围识别
根据既有研究成果,选择中心城镇非农人口数、城乡建设用地面积和地区生产总值的几何平均数作为城市综合规模指数[21],具体计算公式为

由于淇滨区发展时间尚短,根据2014年地区生产总值,淇滨区地区生产总值仅排名第3位,但与2013年相比淇滨区增速排名第1,并且淇滨区作为鹤壁市政治经济文化中心,具有巨大的发展潜力,故选取淇滨区作为鹤壁市经济中心,考虑到市域尺度内,交通距离影响较小,故将Dij设定为城镇之间的直线距离,计算结果如表4所示。
选择淇滨区与淇县之间的断裂点处场强为边界场强计算辐射范围,主要原因:淇滨区与淇县城市综合规模指数均较大,并且相距较近,具有很大的辐射能量,从表4中也可以看出,2个城镇断裂点处场强明显强于其他断裂点处场强;淇滨区与淇县位鹤壁市中部地带,毗邻多条交通干线,与周围联系密切,有利于对周围城镇产生带动辐射作用。选择各个断裂点处场强平均值作为边界场强计算弱辐射范围,可以从整体上反映各个县(区)中心城镇对周围小城镇的影响范围。辐射范围计算见表5,依据辐射半径绘制辐射范围(图3)。
4 结果与分析
由空间聚集计算结果可以看出,鹤山区、淇滨区、山城区、浚县县城、淇县县城的聚集维数D分别为0.992 1、1.238 7、0.989 4、1.180 2、0.948 2,相关系数r2分别为0.989 6、0.952 2、0.986 9、0.951 1、0.972 8。根据D的地理意义可得,鹤壁市县(区)城镇均具有优化的空间结构,表现出明显的分形特征,城镇体系的空间要素分布从中心城镇向四周呈现密度递减趋势,其中以鹤山区、山城区、淇县县城为中心城镇时,城市分布集中程度较高且聚集程度没有显著差异,当以淇滨区、浚县为中心城镇时,城市分布集中程度较低,且聚集程度明显低于其他3个城镇。从总体上看,鹤壁市城镇体系空间结构仍处于不平衡发展的阶段,笔者认为,一方面是由于地形地貌因素,鹤壁市地形西高东低呈现阶梯式分布,鹤山区、山城区、淇县均位于太行山东麓与华北平原接壤地带,地势相对不平坦,西部多山地制约着城镇的发展,东部为广袤的平原地带,为城镇建设提供了良好的地理条件,周围小城镇围绕中心城镇快速发展,呈现聚集态分布;另一方面是由于历史发展原因,1957年鹤壁市市区建设选址在西北部鹤壁集镇,即现在的鹤山区,1959年鹤壁市市区向南搬迁至山城区,由于鹤壁市前2次缘矿而建的城市发展理念,市区周围基本都是煤炭开采造成的塌陷区,鹤壁市城市扩展受到严重制约。1999年鹤壁市城区迁到中部平原地带,即现在的淇滨区,到现在仅经历十几年的发展,发展时间尚短,且淇滨区和浚县位于中部和东部广袤的华北平原地带,周围小城镇大多以农业为主,城镇之间相距较远,分布较为分散,交通联系还不够密切,对周围城镇吸引能力还有待提升。

表2 鹤壁市两两城镇间欧氏距离矩阵

表3 标度r及其对应的关联函数N(r)


表4 淇滨区与各县区城镇之间的断裂点及断裂点处场强

表5 各县区城镇强、弱辐射范围
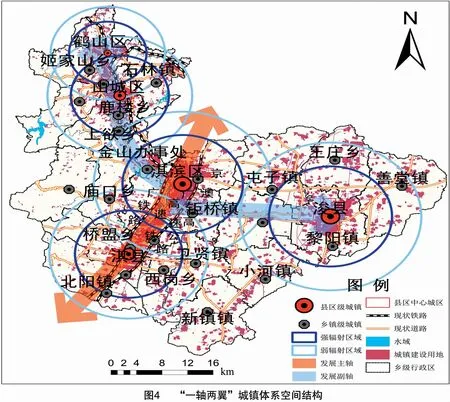
由关联分析可以看出,鹤壁市城镇体系空间结构的关联维数D=1.194 3。根据关联维数的地理意义可知,鹤壁市城镇体系空间相互作用还比较弱,城镇之间相互联系不紧密。从表2中可以得出,鹤壁市城镇体系最近距离(每个城镇与其最近城镇的距离)的均值为5.34 km,其中西北部(鹤山区、山城区)最近距离均值为3.96 km,中南部(淇滨区、淇县)最近距离均值为4.18 km,东部(浚县)最近距离为8.07 km,中西部最近距离均值均小于整体均值,东部最近距离明显大于整体均值,进一步说明地形地貌对鹤壁市城镇体系空间分布的影响。D值接近于1,表明鹤壁市城镇体系分布近似围绕某条地理线集中分布,并呈现“一轴两翼”的特征(图4)。“一轴”即城市发展主轴沿重要交通干线分布,如淇滨区、淇县均沿国道G107、京广澳高速公路、京广高速铁路沿线分布,并逐渐呈现相互接壤融合趋势。“两翼”即老城区城镇组团和浚县城镇组团,通过城市发展副轴实现主城区与“两翼”的互通连接,带动鹤壁市西北部和东部经济的发展。
由图3可以看出,在鹤山区、山城区、淇滨区、浚县和淇县辐射范围内小城镇数量分别为2、6、3、1、5个,虽然山城区辐射范围比浚县小,但由于地形地貌原因以及山城区作为历史上鹤壁市中心城区,经历了长时间的社会经济发展,其影响辐射到的小城镇数量要明显比浚县多,进一步说明地形地貌和历史发展因素对城镇体系空间分布的影响。鹤山区和山城区、淇滨区和淇县辐射范围均存在交汇处并逐渐交融,随着城镇边界的扩展,最终将实现城镇融合,“一轴两翼”的城镇体系空间格局将更加凸显。
基于城镇体系空间分形分析和中心城镇辐射范围识别,对鹤壁市城镇体系空间结构优化提出以下建议:(1)增强城市发展主轴周围城镇集聚功能。依据点轴理论,应立足于淇滨区和淇县地理位置优势,加快推进2个中心城镇接壤,壮大主城区城镇规模,形成鹤淇核心经济轴带。并通过核心经济轴带的辐射,由线到面扩展其影响范围,从而带动周围城镇体系向核心经济轴带聚集,准确定位鹤淇核心经济轴带沿线城镇产业结构,实现区域城镇产业互补,避免城镇间产业同构造成的竞争。(2)准确定位断裂点处和辐射交汇处城镇职能。立足于“一轴两翼”的城镇体系空间结构,在积极发展城市主轴,培育“两翼”组团城镇综合经济实力的同时,构建鹤壁市“多轴带网络型”城镇体系空间结构(图5),增强轴带节点处重点城镇的经济实力,形成鹤壁市经济增长极网络式分布,逐步实现鹤壁市城镇体系向高级稳定状态过度,从而提升鹤壁市城镇体系综合实力。(3)加快鹤壁市内综合交通网络建设。沿城市发展轴线完善交通基础设施,发挥城镇体系沿交通干线集中分布的地理区位优势,提升城市发展主轴同周边各个小城镇的联系密切程度,引导资源在核心城镇间合理配置。
5 结论与讨论

本研究基于分形理论和场强模型,运用ArcGIS空间分析方法,测算了鹤壁市县(区)中心城镇聚集维数和鹤壁市城镇体系的关联维数,识别了县(区)中心城镇强、弱辐射范围,结果表明:(1)县区中心城镇城镇体系空间结构均具有明显的分形特征,鹤山区、山城区、淇县城镇体系空间结构聚集程度相差不显著,但均高于淇滨区和浚县城镇体系空间结构聚集程度,其原因可能是由于鹤壁市地形地貌因素和历史发展原因共同导致。(2)鹤壁市城镇体系整体关联维数D =1.194 3,说明鹤壁市城镇体系空间相互作用还比较弱,城镇之间相互联系不紧密,由于地形地貌原因,西部与中部城镇间联系相对紧密,东部地处广袤平原地带,城镇间联系相对不紧密;城镇体系近似沿国道G107、京广澳高速公路、京广高速铁路分布,其空间结构呈现“一轴两翼”的分布特征。(3)在县(区)中心城镇辐射影响力方面,淇滨区和浚县辐射范围相差不明显,但均明显大于鹤山区、山城区和淇县,由于地形地貌原因,其城市综合规模还需提升,对周围小城镇的辐射影响力还需进一步增强。
城镇体系是一个复杂开放的系统,其空间结构是动态演化的结果,是由其内部各个结构和外界其他系统共同作用形成的,本研究仅揭示了其城镇体系空间结构的分布特征、联系紧密程度及县(区)中心城镇辐射范围,并对5个县(区)进行了横向对比分析。在方法上采用鹤壁市城镇建设用边界几何中心,相比传统以行政区为几何中心进行测度,结果更符合实际情况,但在城镇体系空间结构纵向历史演变趋势方面分析较少,对城镇体系系统内部结构相互作用机理分析还不够明确。

