一个新型四维混沌系统的构造与应用
卢辉斌,薛 瑶,赵 玲,孙海艳
(1.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2.燕山大学 河北省信息传输与信号处理重点实验室,河北 秦皇岛 066004;3.河北建材职业技术学院 机电工程系,河北 秦皇岛 066004)
0 引言
混沌具有的混合特性与密码学中的扩散和混乱存在一定的对应关系[1]。并且,混沌系统所具有的特殊特性,如对初始值的敏感性、较强的伪随机特性、长期不可预测性等[2],使混沌在密码学中广泛应用,保证了加密信息的安全。一个有效的加密算法要想抵御穷举攻击[3],必须对密钥有极端的敏感性,并且有足够大的密钥空间。低维混沌映射具有数学模型简单、产生混沌序列效率高等优点[4],但存在安全性低、随机性较差、密钥空间小等缺点。与之相比,高维超混沌具有良好的序列随机特性,密钥空间足够大,动力学行为更不可预测,安全性高[5],所以对基于超混沌系统的信息加密来说,一般的破译方法很难破译。
本文利用新四维超混沌系统产生的混沌序列,结合神经网络具有记忆反馈的特点[6-7],将其应用到图像的像素值置乱中,使加密算法得到优化。文献[8]采用自治三维混沌系统对彩色图像单像素比特位进行加密操作,可有效抵抗差分攻击,克服了对图像整体像素置乱的缺点。但是该算法采用三维混沌系统,密钥空间小,安全性不高。文献[9]设计了一种具有动态可变的基于超混沌系统的加密算法,若明文与混沌序列发生微小的变化,都会带来完全不同的密钥流,具有较好的安全性。但是该算法采用超混沌Chen系统,其产生的混沌信号随机特性不强,初值敏感性不高。
针对上述问题,本文在三维混沌系统的基础上,引入第四维系统变量w,构建了一个新型的四维超混沌系统,并分析了其非线性动力学特征。结果表明,其具有良好的混沌特性并且在混沌程度、初值敏感性以及混沌信号的随机性方面均优于超混沌Chen系统。然后将新系统应用到图像加密算法中,该算法基于Hopfield神经网络,对图像各分量的单像素比特位进行加密操作。最后利用MATLAB对研究成果进行仿真,分析加密效果。
1 新四维超混沌系统
1.1 数学模型
新四维超混沌系统的数学模型可用下式表示:
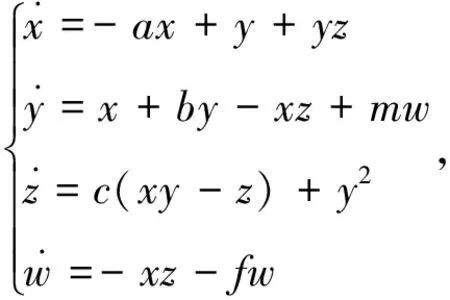
(1)
式中,w为新引入的系统变量,m和f为新引入的系统参数,取m=2,f=0.01,当a=30,b=6,c=15时,系统存在一个典型的混沌吸引子。下面验证混沌吸引子运动轨迹的遍历性特征,利用MATLAB仿真各平面的吸引子相图,如图1所示。
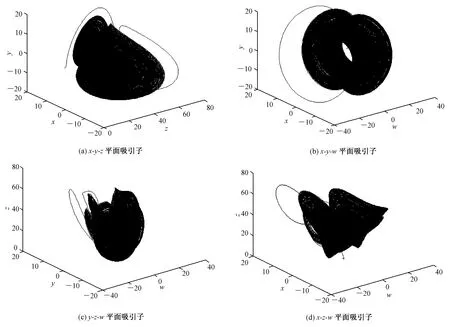
图1 新四维超混沌系统的吸引子相图
Fig.1 Attractor phase diagram of the new four-dimensional hyperchaotic system
1.2 耗散性和吸引子存在性
通过计算
(2)
的值来判断新系统的耗散性。将系统参数a、b、m、c、f的值代入可得ΔV=-a-b+c-f=-30+15-6-0.01=-21.01<0,可知新系统是耗散的,并且会以
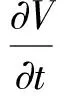
(3)
形式收敛,即体积元V0在t时刻收敛为V0e-a-b+c-f,当t→∞时,所有体积元以指数率e-a-b+c-f收敛到0,所以轨迹线被限定在一个体积为0的集合上,且它渐进地固定在一个吸引子上。
1.3 平衡点及其稳定性
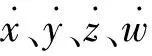
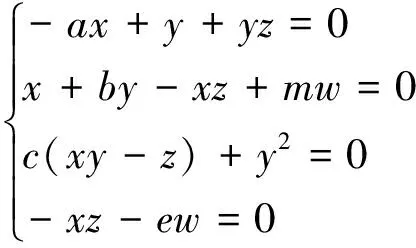
(4)
求解上式方程组,可得该系统有5个平衡点S1、S2、S3、S4、S5,它们的值分别为
S1=(0,0,0,0),
S2=(-16.043 7,0.148 4,2.140 0,1.080 9),
S3=(16.043 7,-0.148 4,-2.140 0,1.080 9),
S4=(-29.658 5,-0.142 9,3.983 8,-2.075 9),
S5=(29.658 5,0.142 9,-3.983 8,-2.075 9)。
接下来验证5个平衡点的稳定性,先将系统平衡点线性化,然后根据Jacobian矩阵求解特征根,根据特征根的分布分析平衡点的稳定性。以S1为例,在平衡点S1(0,0,0,0)处进行线性化,得到Jacobian矩阵J1:
其特征方程为
|λI-J1|=0,
(5)
得到S1的特征根分别为:λ1=-30.022 2,λ2=15.022 2,λ3=-6.000 0,λ4=-0.010 0。四个特征根中,λ1、λ3、λ4为负实根,λ2为正实根,不全为负实根,则S1为不稳点鞍点[11]。对于平衡点S2和S3,S4和S5,它们是两两关于w轴对称存在的,只分析其中的一个即可,计算方法和S1相同,S2的特征根为λ1=-29.950 2,λ2=5.520 3+37.997 0j,λ3=5.520 3-37.997 0j,λ4=-2.100 4,其中j2=-1。λ1、λ4为负实根,λ2、λ3是一对实部为正的共轭复根,所以平衡点S2和S3为不稳定的鞍点,同理可得S4和S5也为不稳定的鞍点。
上述计算结果表明不稳定的鞍焦点分布满足Shilnikov定理[12],从而证明了该系统在一定条件下会产生混沌。
1.4 Lyapunov指数
新系统的两个正的Lyapunov指数分别为1.379 4和0.609 5,可以看出,该系统符合超混沌系统具有两个正的Lyapunov指数的条件。
超混沌Chen系统的数学模型为
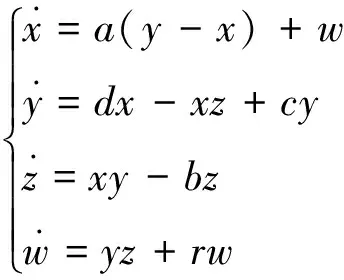
(6)
当系统参数a=35,b=3,c=12,d=7,0.085≤r≤0.798时,系统变现为超混沌态,本文中取r=0.6,此时,超混沌Chen系统的最大Lyapunov指数为0.567,显然,新系统的最大Lyapunov指数比较大,指数越大,说明混沌特性越明显,混沌程度越高,整个吸引子域被轨道覆盖的速度越快。
下面验证新系统的Lyapunov维数是否为分数维,若是,则其为混沌系统,验证公式为
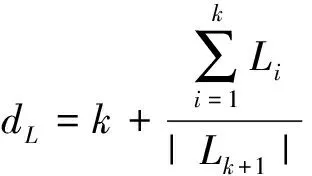
(7)
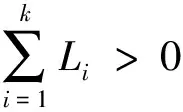
1.5 系统对初值的敏感性
对于初始值的微小改变,混沌系统会表现的十分敏感,这个性质对图像加密十分有利。对四个系统变量的初值作微小改变,即x,y,z,w均加上0.000 000 000 1,经过系统的数次迭代后,观察新系统的变量波形变化图,如图2(a)所示。在相同条件下,观察超混沌Chen系统的变量波形图,如图2(b)所示。
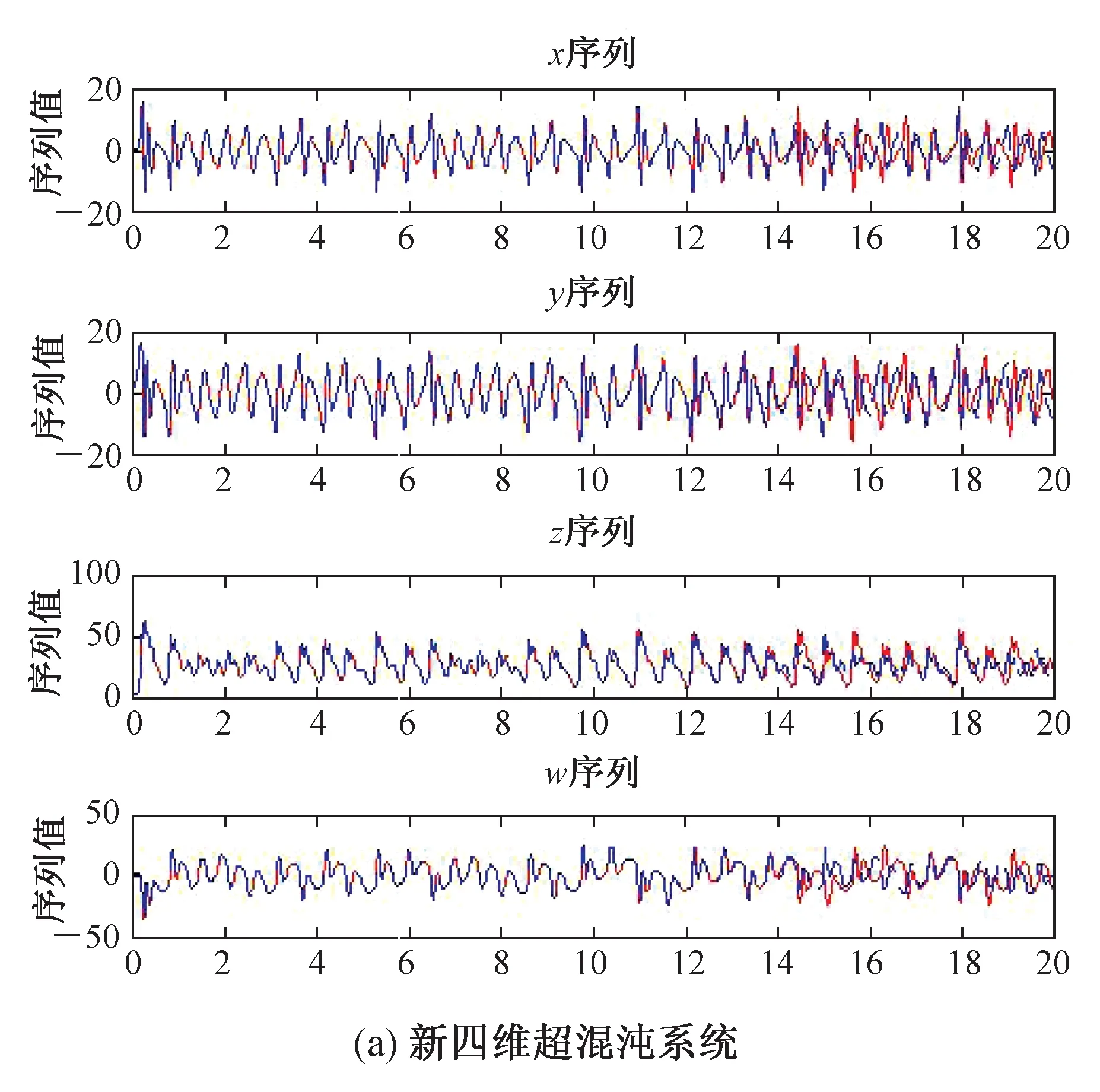
图2 新系统和超混沌Chen系统的敏感性比较
Fig.2 Comparison of sensitivity between new system and hyperchaotic Chen system
如图2所示,两个系统在使初始值发生微小改变的同等情况下,超混沌Chen系统的波形变化不明显,而新系统的波形变化则十分明显。通过比较图2(a)和图2(b)可知,新系统对初始值的敏感性更好,更适合应用到图像加密领域。
1.6 混沌信号
如果混沌信号的随机性不强[13],容易受AR模型预测和相空间重构法的攻击。所以参考文献[14]对系统所产生的混沌信号进行处理,使其分布均匀,处理方法为
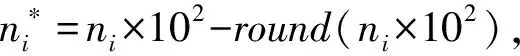
(8)

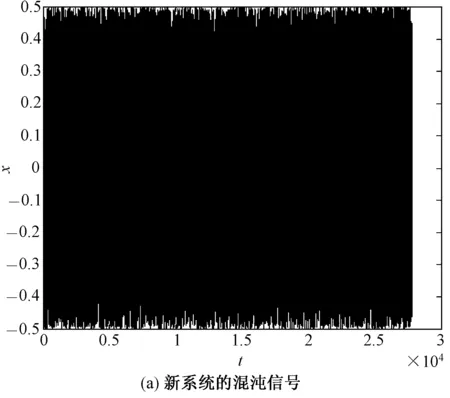

图3 新系统和超混沌Chen系统混沌信号的随机性比较
Fig.3 Comparison of randomness of chaotic signal between new system and hyperchaotic Chen system
由图3可以看出,经式(8)处理后,新系统与超混沌Chen系统产生的混沌信号均呈现出均匀分布的态势,但仔细观察会发现,新系统的混沌信号分布更加均匀,即随机特性更优,具有更强的抵御相空间重构法攻击和AR模型预测攻击的能力。
2 新四维超混沌系统的应用
将新四维超混沌系统应用于彩色图像加密算法中,参考文献[15],将基于Hopfield网络的彩色图像加密算法,与四维超混沌系统相结合,通过实验仿真观察加密效果与算法性能。
2.1 图像像素位置的置乱算法
利用数学模型(1)通过系统迭代产生混沌序列,提取大小为M×N×3的彩色图像的R、G、B三分量,分别选择混沌序列的三个序列置乱彩色图像的三分量。下面以X、Z和W序列对R分量进行置乱为例,来说明此算法的像素位置置乱思路,步骤如下:
步骤1:选取Z序列中M项,W序列中M项,相加构成{z1m,m∈[1,M]}{z1m,m∈[1,M]},选取X序列中N项构成{x1n,n∈[1,N]}{x1n,n∈[1,N]}。
步骤2:根据式(9)得到置乱序列{hrm,m∈[1,M]},其中hrm∈[0,N-1]。将分量R从第1行到第M行,根据其与序列hrm相对应的值进行循环右移,然后转置,得到大小为N×M的矩阵
hrm=⎣|zlm×1014|」%N。
(9)
步骤3:根据式(10)得到置乱序列vrn,vrn∈[0,M-1],对经过第一次置乱得到的分量R再次置乱。根据其与序列vrn相对应的值,从第1行到第N行进行循环右移,然后再次转置,得到置乱后大小为M×N的R分量
vrn=⎣|xln×1014|」%M。
(10)
G分量和B分量的置乱方法和R分量的类似。可从Y序列和W序列中各选取M项相加,从Z序列中选取N项对G分量进行置乱;从X序列和W序列中各选取M项相加,从Y序列中选取N项对B分量进行置乱。若想取得更好的加密效果,可重复进行上述步骤。
2.2 图像像素值的置乱算法
利用离散型Hopfield网络具有反馈这一特点,将其应用于图像像素值的置乱算法中。具体操作步骤如下:
步骤1:提取大小为M×N×3的彩色图像的R,G,B三基色分量,按列将三分量的像素值展成向量{Irk},{Igk},{Ibk},然后将这三个向量转换成二进制序列,用{prk,i},{pgk,j},{pbk,i}表示,其中k∈[1,M×N],i∈[0,7]。Irk,Igk,Ibk与prk,j,pgk,i,pbk,i之间满足
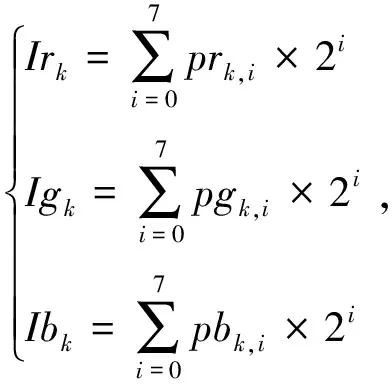
(11)
式中,k表示第k个像素值,i表示第i比特位。
步骤2:利用数学模型(1)产生四维混沌序列,选取X序列、Y序列和Z序列,将它们的长度截取为M×N,以便进行图像像素值置乱。对截取后的序列进行处理映射,得到序列{xk},{yk},{zk},计算方法为
(12)
步骤3:将{xk},{yk},{zk}转换为用{w1k,i},{w2k,i},{w3k,i}表示的二值序列,如式(13)所示:
(13)
步骤4:根据二值序列{w1k,i},{w2k,i},{w3k,i}的取值,得到置乱的权值序列{ww1k,i},{ww2k,i},{ww3k,i},当二值序列值取1时,权值为1,当二值序列取0时,权值为-1。然后利用混沌序列的二值序列{w1k,i},{w2k,i},{w3k,i}图像三基色分量的二进制序列{prk,i},{pgk,i},{pbk,i}和置乱的权值{ww1k,i},{ww2k,i},{ww3k,i}产生阈值序列{yu1k,i},{yu2k,i},{yu3k,i},它们之间的变换关系为
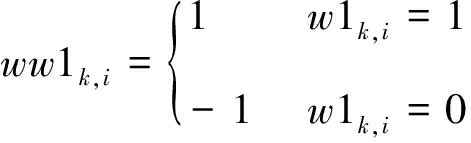
(14)
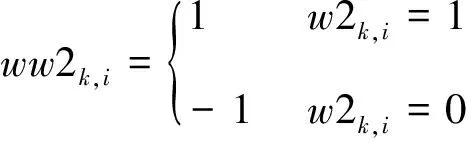
(15)
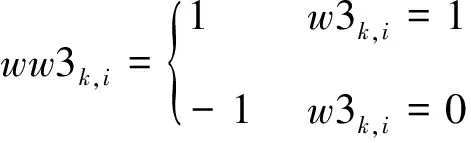
(16)
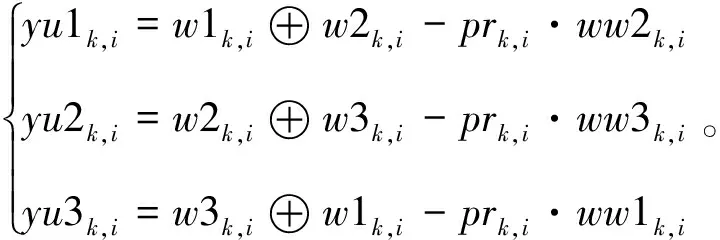
(17)
步骤5:对像素值进行置乱,得到序列{Crk,i},{Cgk,i},{Cbk,i},计算方法为
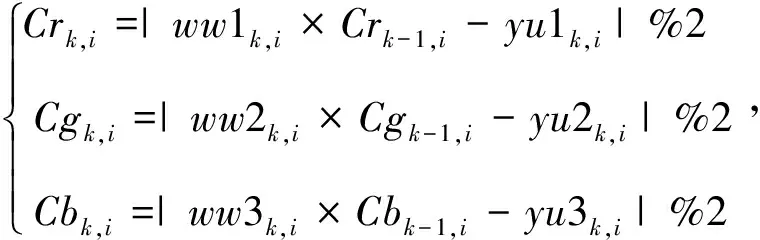
(18)
式中,Crk,i,Cgk,i,Cbk,i分别表示Crk-1,i,Cgk-1,i,Cbk-1,i后一个像素值的密文。在求解Cr1,i,Cg1,i,Cb1,i的过程中,需要知道Cr0,i,Cg0,i,Cb0,i将三分量最后一个像素值的二进制序列{prM×N,i},{pgM×N,i},{pbM×N,i}代入公式进行计算,即可得到Cr0,i,Cg0,i,Cb0,i。
步骤6:将经过置乱后的二进制像素值转换成十进制,对R、G、B分量的十进制信息进行重新组合,形成置乱图像,图像的加密过程至此结束。
在解密求解原像素值pr0,i,pg0,i,pb0,i时,可用prM×N,ipgM×N,i,pbM×N,i代替Cr0,i,Cg0,i,Cb0,i,即为加密的逆过程,计算方法为
(19)
3 实验仿真及加密效果分析
3.1 图像加密效果分析
在MATLAB R2013a环境下,对此算法进行实验仿真,分析图像加密效果图。设置新四维超混沌系统的参数、初始值以及积分步长,其中a=30,b=15,c=6,m=2,f=0.01;x0=2,y0=1,z0=3,w0=1;h=0.01。系统迭代M×N+5 000次,并舍弃前5 000次。选择大小为256×256×3的彩色图像,并按照上述的加密算法进行操作,得到的仿真结果如图4所示。
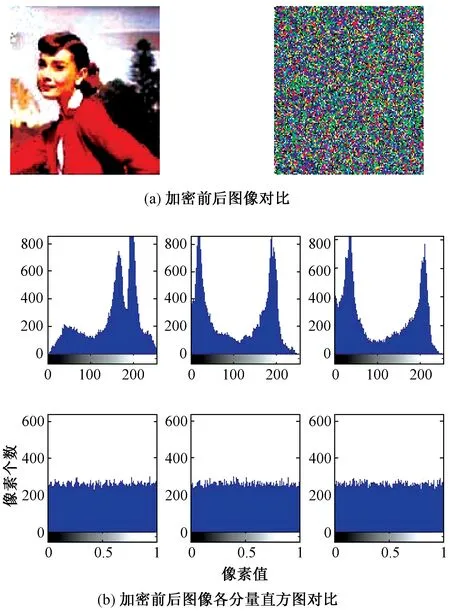
图4 图像加密效果图
Fig.4 The result figures of image encryption
从图4(a)中可以看出,该算法成功地对图像进行了加密,效果明显,原图像的像素点和像素值被彻底地置乱,密图和原图相差巨大,说明单像素混沌加密算法能够有效的加密图像。从图4(b)中可以看出,加密前后,图像R、G、B分量的像素直方图完全不一致,加密图像的直方图分布更加均匀,这说明置乱操作已扩散到每一个像素点,加密效果良好。
3.2 密钥敏感性测试
下面实验仿真正确解密和错误解密的效果图。以x0为例,对加密密钥的敏感性进行测试,将初始值x0加上10-10,即x0存在10-10的误差时,得到错误解密图像,如图5所示。
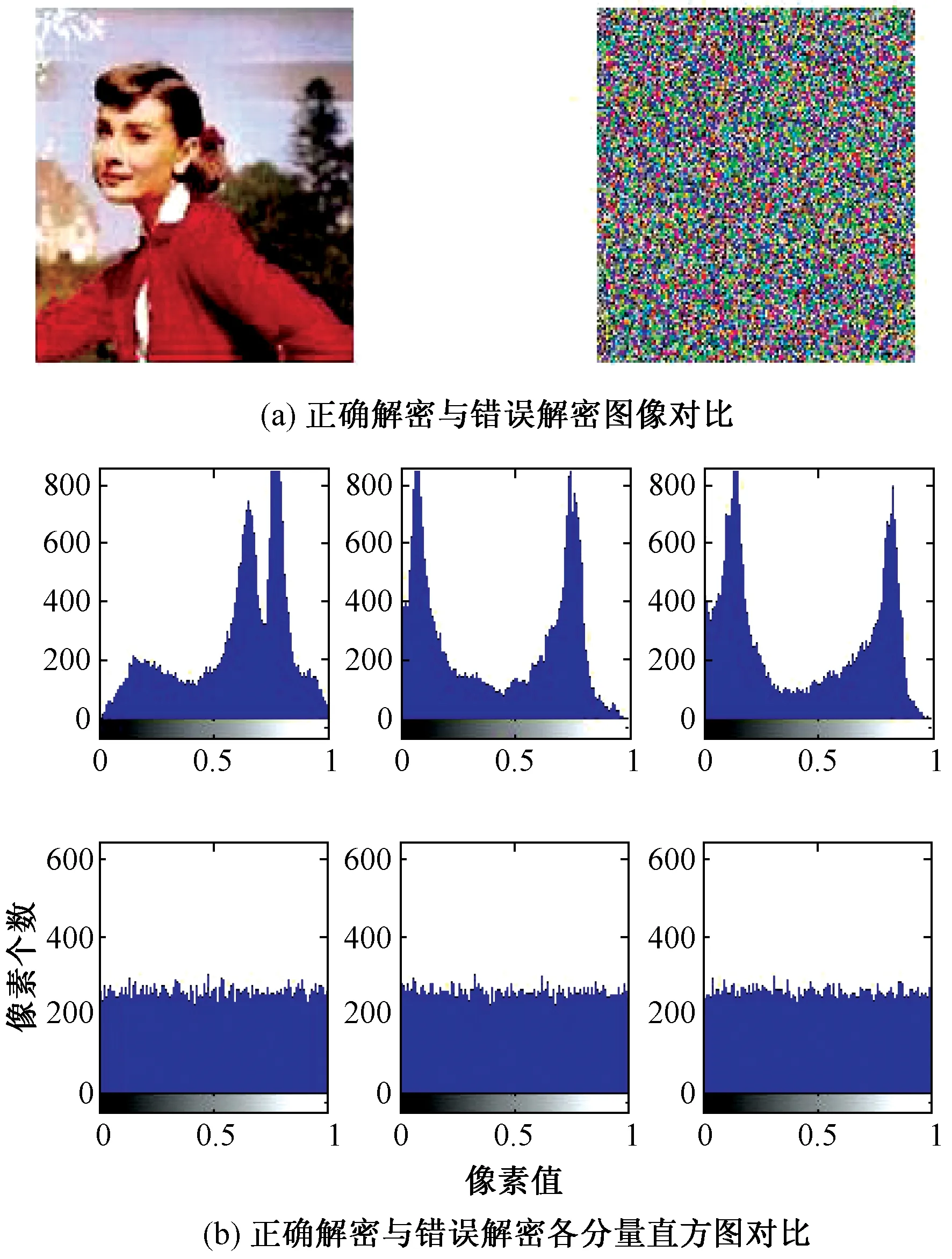
图5 图像正确解密与错误解密效果图
Fig.5 The result figures of image correct decryption and error decryption
图5(a)对比了正确解密与错误解密的图像变化,可见该算法的正确解密操作可以恢复出原图,然而当有微小误差的时候,则无法进行正确解密,说明该算法对密钥极端敏感。图5(b)对比了正确解密与错误解密时,R、G、B分量的像素直方图分布情况,可见正确解密可以得到原直方图,错误解密则不能恢复原直方图,并且直方图分布仍然十分均匀,说明该算法抗攻击性能良好,错误解密操作不会泄露原图像的信息。
3.3 统计特性分析
从像素相关性和抗差分性能两个方面对加密后的图像进行统计特性分析。
3.3.1 像素相关性
一般通过分析像素的相关性来进一步分辨算法的优劣。原图像的像素相关性比较强,经过一系列的加密操作,得到加密图像,加密图像相邻像素的相关性越弱,说明加密算法越优良。根据式(20)~(22)计算相邻像素的相关系数:
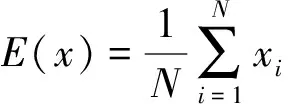
(20)
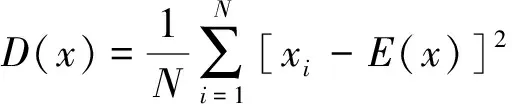
(21)
(22)
(23)
式中,rxy越接近于1,表示像素相关性越强,rxy越接近于0,表示像素相关性越弱。
随机取原图和密图三分量在横向、纵向、对角方向的1 000对像素值,计算相邻像素相关性,结果以绝对值的形式表示,如表1所示。
表1 原图与密图相邻像素的相关系数对比
Tab.1 Comparison of the correlation coefficient of adjacent pixels of an original image and an encrypted image
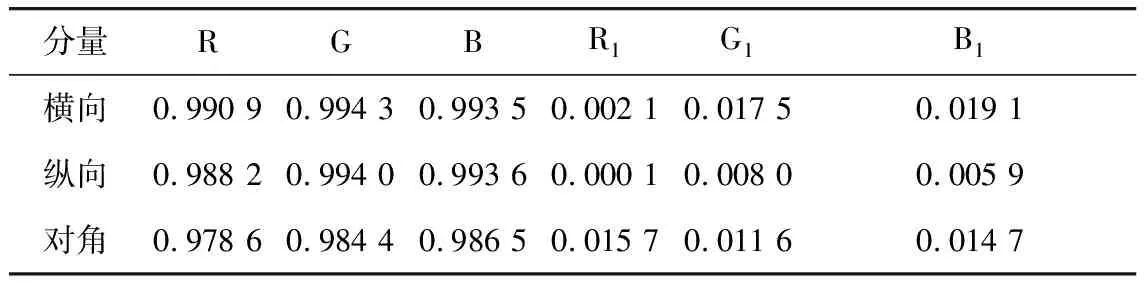
分量RGBR1G1B1横向0.990 90.994 30.993 50.002 10.017 50.019 1纵向0.988 20.994 00.993 60.000 10.008 00.005 9对角0.978 60.984 40.986 50.015 70.011 60.014 7
由表1可看出,原图R、G、B分量在3个方向上的像素相关系数的绝对值都十分接近于1,相关性很强,而密图相关系数的绝对值都十分接近于0,相关性很弱,说明该算法通过一系列操作,降低了像素的相关性,达到了加密的目的,加密效果良好。
3.3.2 抗差分性能
我们常用两个变化率的值来定量说明加密算法的抗差分攻击性能:像素变化率和像素平均强度变化率。在MATLAB R2013a环境下,设加密后原图像和改变一个像素值后的图像的矩阵形式为HD、HD1,比较像素值,若有HD(i,j)≠HD1(i,j),则D(i,j)=1,反之D(i,j)=0,计算公式为
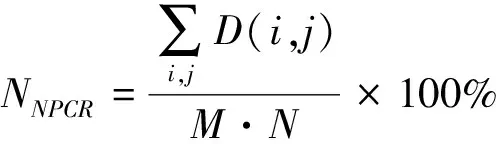
(24)
(25)
分别改变原图像三分量的一个像素点,得到对应的像素变化率和像素平均强度变化率值,见表2。
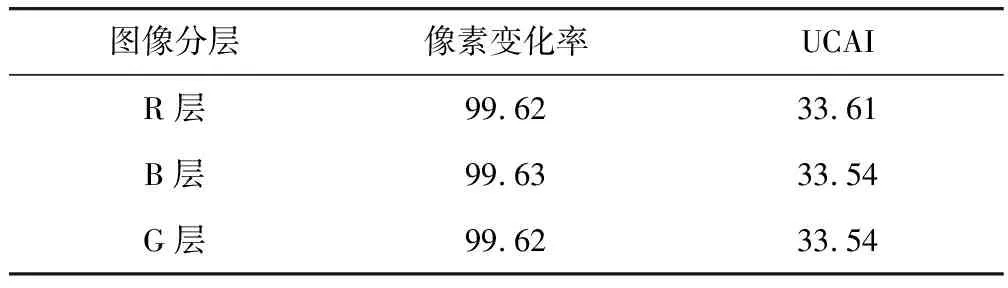
表2 R、G、B分量的像素变化率值和像素平均强度变化率值Tab.2 Values of NRCP and UCAI of the R,G,and B components %
像素变化率和像素平均强度变化率的理想值为99.609%和33.464%[16],由表2可以看出,图像R层、G层和B层的像素变化率值和像素平均强度变化率值都十分接近理想值,也就是说该算法对作用于原图的微小变化会表现的非常敏感,从而说明了其可以有效地抵御差分攻击。
3.4 抗干扰性分析
本文通过对加密图像进行剪切,加入不同强度不同种类的噪声干扰,来验证该加密算法的抗干扰能力,在MATLAB R2013a环境下进行实验仿真,测试结果如图6所示。



图6 抗干扰攻击仿真图
Fig.6 Simulation images of resisting jamming attack
在现实情况中,信息的传输容易受到各种干扰与攻击,所以要求图像加密算法具有较强的鲁棒性。由图6可以看出,对于剪切与噪声攻击,该算法可以正确地解密恢复出原始图像,说明其安全有效,具有良好的抗干扰能力。
4 结论
本文阐述了一个新型四维超混沌系统的构造与应用。实验结果表明,新构造的四维系统符合混沌系统的各个指标,具有良好的混沌动力学特征,并且在敏感性、混沌信号的随机性等方面均优于超混沌Chen系统。将新系统应用于基于Hopfield网络的单像素加密算法中,结果显示,加密效果良好,并且该算法可有效抵抗差分攻击、剪切攻击和噪声攻击,安全有效。本系统的4个初始值和参数m、f可作为密钥,再加上初始迭代次数,说明有足够大的密钥空间,可以抵御穷举攻击。新引入的第四维方程为非线性方程,其复杂度更高,混沌特性更优良,将其应用到加密算法中安全性更高,但是对系统进行迭代产生混沌序列时,计算量大且计算过程复杂,致使算法的时间复杂度相比较三维混沌系统和第四维为线性方程的超混沌系统有稍许差距。在今后的工作中,考虑尽量均衡混沌特性与算法复杂度的关系,做到最优。

