高阶振型振动实验装置研制与教学应用

庞新宇, 江旺旺, 任智军

(1. 太原理工大学 机械工程学院, 山西 太原 030024； 2. 煤矿综采装备山西省重点实验室,山西 太原 030024； 3. 西安交通大学 机械工程学院, 陕西 西安 710049)

振动学涉及机械类的多门专业课程,高阶振动系统又是振动学中的一类研究对象。为了使学生对振动现象有更深刻的认识,加深对理论知识的理解,各种振动实验装置及教学系统相继开发。江苏大学的李建康等[1]建立了多自由度系统模态振型实验台,用于研究在频率可变的水平激励下各个质量块的振型状态；中国矿业大学的张晓光等[2]搭建了含有故障的齿轮减速器振动实验装置；华中科技大学的何岭松[3]设计了用于描述多自由度振动模型的仿真系统；蒋志峰[4]等、张予等[5]利用Matlab对单自由度系统受不同激振频率的受迫振动响应进行了仿真分析；付志一等[6]设计了三自由度扭振实验装置,研究系统本身的振型及附加质量和刚度对于系统振型的影响；梁庆等[7]基于LabVIEW开发了多自由度悬臂梁振动实验教学系统,可实现单自由度、两自由度和三自由度等多种实验方案,并利用有限元软件对模型进行模态分析与比较；张蔚波等[8]研制了简支梁形式的振动实验教学装置,分析了不同性质激励下的响应；李兆军等[9]研制了包含离散质量、连续梁、轴和组合结构的综合振动实验装置。上述的振动实验装置及教学系统,有的局限于单自由度的振动研究,有的则专门针对某一实体部件而进行研究,有关高阶振动的振型可视化及固有频率的计算则涉及非常少,能够在理论和实验两方面都能激发学生的学习兴趣、增强学生的理解能力的装置更少。

为此本文研制了一套适用于高阶振型振动系统教学的实验装置。该装置可实现对固有频率的理论计算和实验测试,可直接观察不同阶次的振型。该实验装置可根据需要设计为不同的阶数,本文以三阶系统为例进行介绍。

1 实验装置结构设计

本实验装置主要由主体框架、振动传感器、千分表、磁性表座、立柱、定滑轮、激振器、信号发生器、数据采集仪和频闪仪等组成,如图1所示。主体框架为3层钢架结构,由空心钢管和侧板固接；振动传感器为加速度传感器,固定在主体框架的顶层侧板上；千分表主要用来测量框架受到静力作用时各层的位移变化量；立柱用于固定测算振动体柔度矩阵的定滑轮；激振器为主体框架提供受迫振动的激励,通过信号发生器改变其振动频率,经实验验证,激振器与主体框架的连接位置对系统的固有频率没有影响,为了方便安装,本文将激振器与底层侧板相连；数据采集仪主要将测得的振动信号传递给安装有动态分析软件的上位机,以此来实时显示振动信号的时域及频域波形图,便于学生更为直观地了解振动信号的固有频率及振幅。

图1 实验装置结构图

2 实验方案

该装置的实验方案如图2所示,主要包括理论计算、自由振动实验、受迫振动实验3部分。理论计算通过重物在主体框架的某个节点上作用一定的载荷,使得各层钢管产生一定的变形,由千分表测得位移变化量并输入基于柔度法编写的Matlab程序中,从而在理论上计算出各阶振动的固有频率及振型。实验方法分别通过锤击法模拟自由振动，和由激振器模拟的强迫振动,使得主体框架产生振动,由加速度传感器将振动信号传递给数据采集仪和安装有DHDAS动态信号采集分析软件的上位机,以此来直观地观察高阶振动的各阶固有频率及振幅变化。利用频闪仪可观察到受迫振动时各阶频率的振型,并与理论计算结果进行比较,检验模型和算法的准确性。

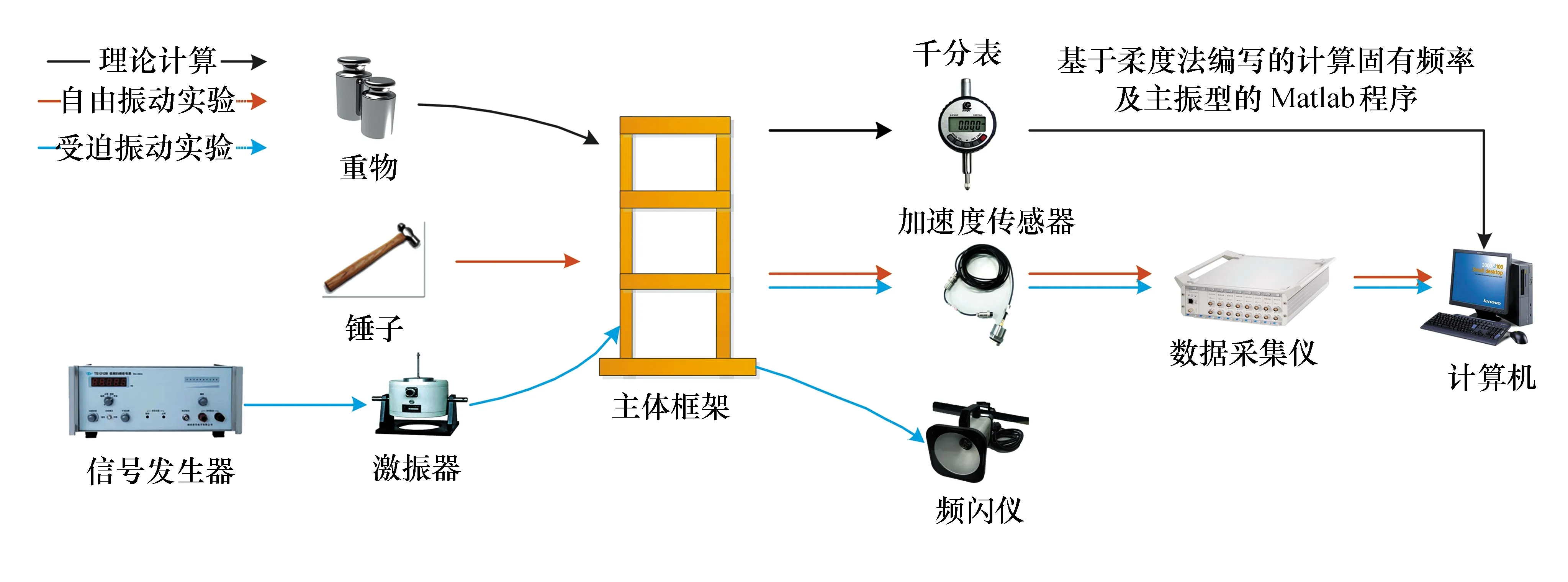
图2 实验方案

该实验装置的主要目的在于给学生提供一个能够对高阶振动的振型及固有频率产生一种直观印象的实验平台。通过理论计算方法和实验方法,学生不仅可以从理论上掌握求解相关高阶振动的固有频率及其振型的方法,而且还可以运用所学的理论知识,通过实验测得和观察高阶振动的固有频率及振型,加深对高阶振动的理解。

3 理论计算方法

本文基于柔度法计算固有频率及振型。根据柔度影响系数aij的定义,在j点上作用的单位载荷所引起的i点的位移,可以通过施加在主体框架上力的大小以及各层框架的位移变化量来计算出该系统的柔度矩阵,进而求出固有频率及振型。

3.1 柔度法

由动力学理论[10-11]可知,多自由度系统的无阻尼自由振动的微分方程为

K-ω2MX=0

(1)

式中，K为系统刚度矩阵,M为系统质量矩阵,ω为系统固有角频率，X为位移列矩阵。

(λ2I-D)X=0

(2)

式中I为单位矩阵。

方程(2)有非零解的充分、必要条件是其系数行列式为零,即：

|λ2I-D|=0

(3)

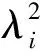
由于柔度矩阵H与刚度矩阵K之间的关系为H=K-1,所以可通过对系统的柔度矩阵进行测算来计算固有频率。

3.2 编程思路

基于上述的柔度法编写Matlab程序,实现软件计算固有频率和振型。

测量原理如图3所示,在实验装置的节点1处施加15 N的载荷F,由千分表测量各层的位移变化量,得到x11、x21、x31,同理分别在节点2、3处作用相同的载荷,可以测得各层相应的变化量。根据柔度影响系数的定义,并结合载荷大小,即可求出柔度矩阵。

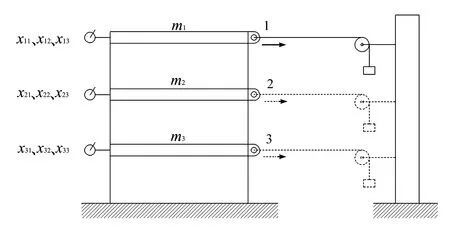
图3 柔度矩阵测量原理图

程序编制步骤如下：

(1) 综合考虑各层空心钢管、侧板以及振动传感器的质量,并输入各层框架的质量：m1、m2、m3,单位为g；

(2) 输入各层的位移量：x11、x12、x13、x21、x22、x23、x31、x32、x33,单位为mm；

(3) 构造质量矩阵M和柔度矩阵H如下：(其中F=15 N)

(6) 输出f1、f2、f3(由小到大排列),Y(1)、Y(2)、Y(3)(与fi顺序对应)。

4 实验方法

4.1 自由振动实验

自由振动实验：即在实验开始时使主体框架受到某一冲击载荷,在振动的过程中不再承受其他外部激励,通过对采集到的振动信号进行频谱分析[12],找到对应于各个峰值的频率即为各阶振动的固有频率。

本文的自由振动实验基于锤击法,振动传感器将采集到的振动信号传递给数据采集仪和上位机,经频谱分析得到振动信号的幅频特性曲线,幅频特性曲线图中的峰值所对应的频率表示振动体的固有频率,峰值的个数则代表高阶振动体固有频率的阶数。图4为3层框架自由振动实验的幅频特性曲线。

图4 自由振动实验幅频特性曲线

由图4可知，自由振动的幅频特性曲线图共有3个峰值,即三层框架结构振动体的固有频率为3阶,且第一阶、第二阶第三阶固有频率分别为22.21、61.11、95.11 Hz。

4.2 受迫振动实验

受迫振动实验：通过某一频率可变的外部激励持续作用在主体框架上,使得框架结构作受迫振动,对采集到的振动信号进行频谱分析,找出幅值峰值处(即发生共振时)所对应的频率,即为该振动体的固有频率。

本文的外部激励由框架底部的激振器提供,调节与激振器相连的信号发生器的频率,使其由小到大逐渐变化,上位机实时分析振动信号,通过观察幅频曲线,找到发生共振时频谱图的峰值所对应的频率,即为3层框架结构的固有频率。图5为受迫振动实验下3层框架结构的幅频特性曲线,由图5可知受迫振动下3层框架结构的一阶、二阶和三阶固有频率分别为：22.22、61.11、95.11 Hz。

4.3 振型法

振动体共振时其振型可通过频闪仪进行观察。当3层框架结构发生共振时,调节频闪仪的频率,使其与结构体共振频率接近或相等,即可清楚地观察到框架结构的振型状态。图6为3层框架结构共振时各阶固有频率所对应的振型。

图5 受迫振动实验幅频特性曲线

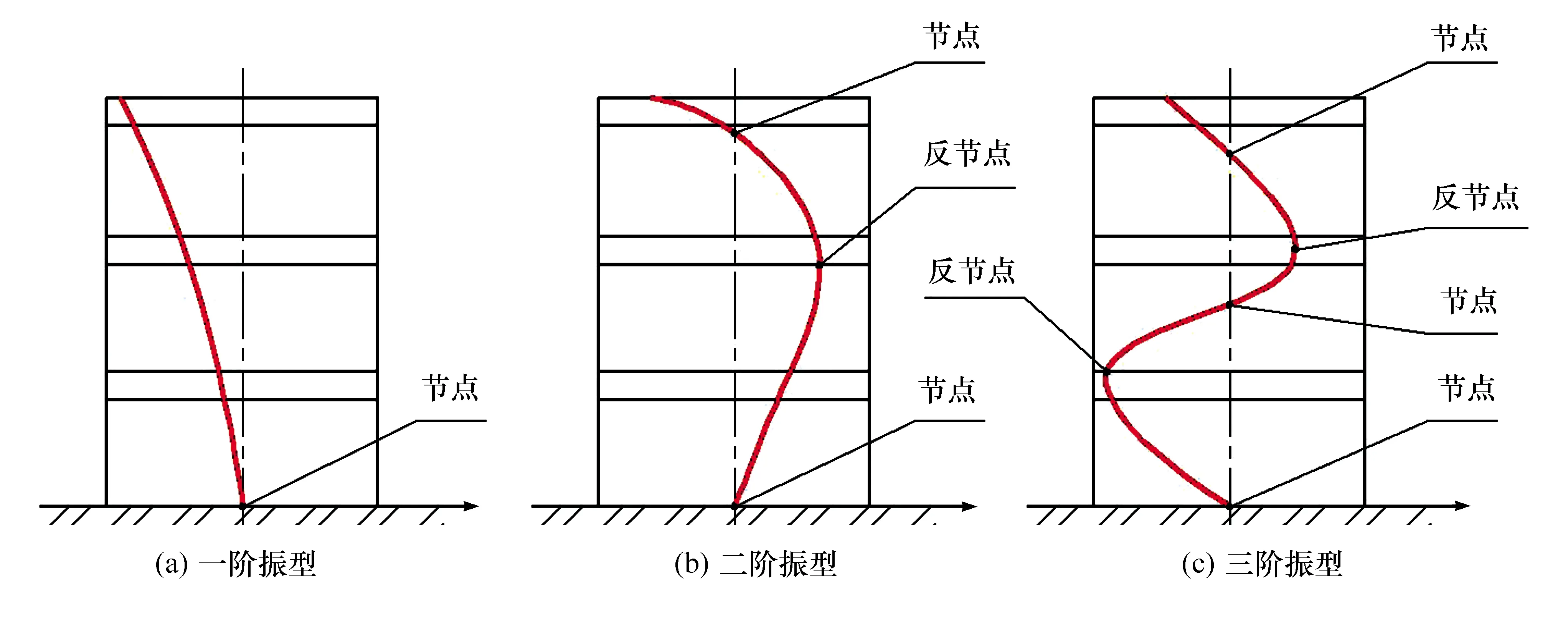
图6 各阶固有频率对应的振型图

在高阶振动振型中,振幅为零的点即为振型节点,振幅最大处即为反节点。由图6可以看出,3层框架结构一阶振型只有底座1个节点,二阶振型和三阶振型分别有2个、3个节点,且节点的位置在振动的过程中始终保持不变。

5 实验结果分析

按照理论计算方法的步骤,将各层质量及位移变化量输入到程序中,计算结果如图7所示。

图7 理论计算运行结果图

由图7可以看出,一阶振型均为正值,表明各层之间没有从负向正的节点变化；二阶振型底层和中层为负值,顶层为正值,表明中层与顶层之间存在节点；三阶振型的中间层为负值,其余两层为正值,表明底层与中层、中层与顶层之间分别存在一个节点。各层节点的图形化与图6完全相符。

理论计算、自由振动实验和受迫振动实验得到的3层框架结构振动体的固有频率见表1。

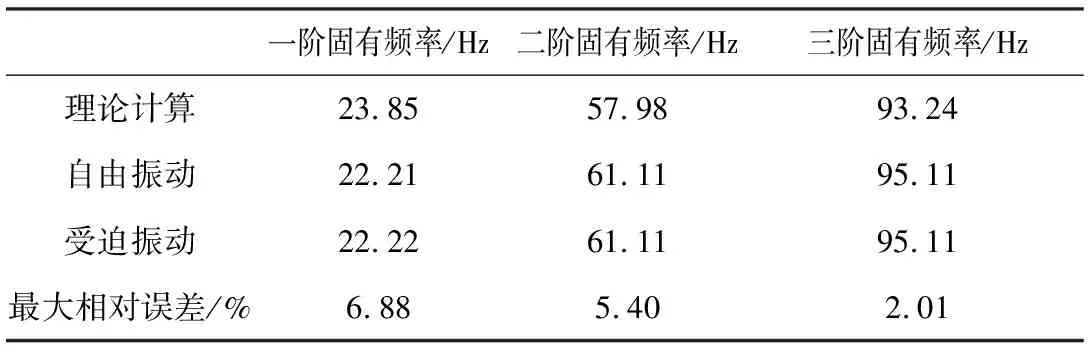
表1 理论计算、自由振动、受迫振动固有频率

由表1可知,实验与理论计算之间存在误差,其中一阶固有频率的相对误差最大,三阶固有频率的相对误差最小。产生误差的原因主要是由于千分表的测量误差、主体框架材料的刚度较大以及加速度传感器质量的影响。

6 结语

机械类专业课程都会涉及到振动学,高阶振型振动实验装置可用于机械振动学、机械故障诊断、理论力学、机械动力学以及机械工程控制基础等课程的实验教学。利用高阶振型振动实验装置,学生从理论和实验两个方面获取高阶振动体的固有频率,并观测其振型的变化,从而加深了对高阶振动系统的认识。该实验装置完善了振动学的教学实验内容,在教学应用中收到了良好的教学效果,提高了学科教学质量。