基于非线性MPC方法的车辆稳定性控制

郝西祥，陈亚伟，邵毅明

(重庆交通大学 a.交通运输学院; b.机电与车辆工程学院, 重庆 400074)

车辆的极限性能很大程度上是由轮胎的非线性力学特征决定的，因此基于模型预测控制(MPC)的车辆稳定性控制的实现取决于预测模型中的非线性系统动力学分析结果。同时由此产生的非线性优化问题给控制器的实时运行带来了很大的挑战。

针对上述问题，许多文献中提出了各种替代NMPC的方法，如线性时变MPC、混合和切换MPC或近似NMPC[1-3]。本文采用显式NMPC方法离线解决优化问题，获得的显式解是一个次优的多变量反馈定律，可以方便地进行实时评估。

本文在设计控制系统的非线性车辆模型时，考虑了纵向和横向轮胎力的相互作用以及车辆转弯时轴荷转移的影响，这对车辆的稳定性控制具有极为重要的作用。此外，本文提出的NMPC代价函数公式具有一定的灵活性，可以较为便捷地在实际车辆上应用。

1 车辆预测模型

1.1 车辆动力学建模

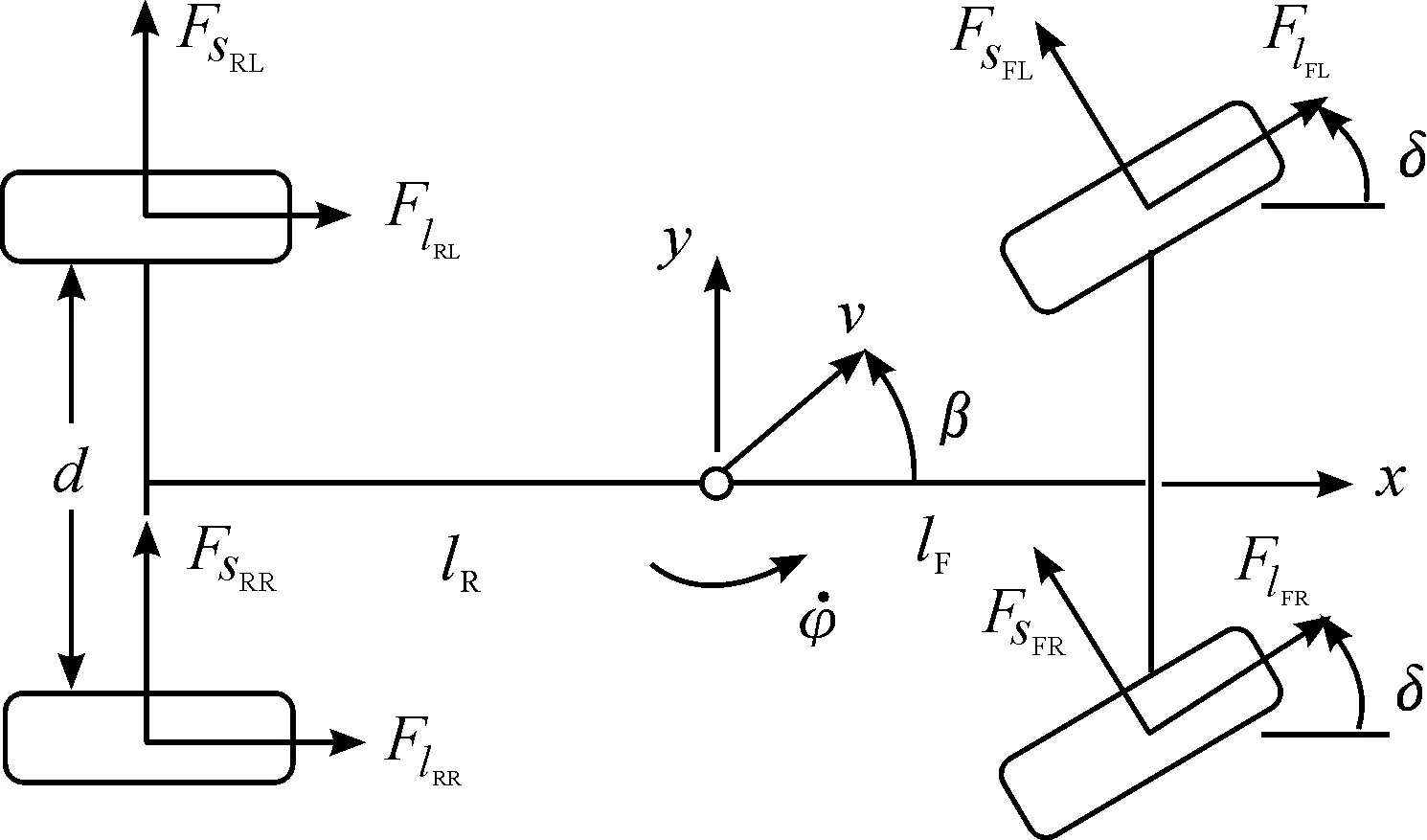
图1 车辆动力学模型

根据牛顿第二定律及力矩平衡公式，得到如下的方程：

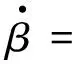
(FsFL+FsFR)cos(δ-β)-

(FlRL+FlRR)sinβ+

(1)

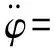
(2)

其中：m为车辆质量；Iz为车辆绕z轴的转动惯量；lF和lR分别是车辆的前后轴距；d为车辆轮距；δ为前轮转角；Flij和Fsij分别是轮胎的纵向力和横向力；下标i=F,R，表示前后轴；j=L,R，表示左右轮。

1.2 轮胎垂直力

垂直轮胎力Fzij的估计考虑了与侧向加速度相关的载荷传递，计算基于式(3)和 (4)中定义的常数。

(3)

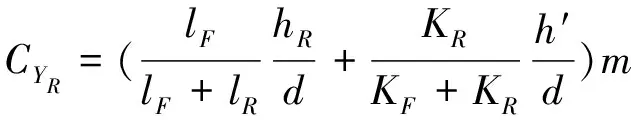
(4)

其中：hF和hR分别是前后悬架的侧倾中心高度，h′是滚动轴与车辆重心之间的距离；KF和KR是前后悬架的侧倾刚度值。由式(3)和(4)可得，垂直载荷估计如下：

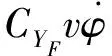
(5)

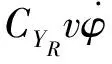
(6)

其中FzRj,stat是单个轮胎的静态垂直载荷。式(5)和(6)中忽略了质心侧偏角速度的影响。

1.3 轮胎受力模型

采用简化的魔术轮胎公式对轮胎侧向力的非线性动力学进行建模，纯侧移工况下的侧向力Fs0ij定义为轮胎侧偏角αij的非线性函数[4]。

Fs0ij=Dsijsin(Csijtan-1(Bsijαij))

(7)

其中：Dsij为峰值因子；Csij是侧向形状因子；Bsij是刚度因子。当Csij和Bsij为常数时，Dsij取决于Fs0ij。根据滑移工况下轮胎横向力和纵向力之间的相互作用，得到轮胎力的线性近似为

(8)

由式(8)可知，组合滑移中的每个横向轮胎力Fsij会减小一个系数，该系数取决于当前估计的纵向轮胎力Flij(制动时Flij≤0)除以其在纯纵向滑动条件下的最大值Dlij。Dlij的值可由纵向轮胎-路面摩擦系数μlpij和垂直轮胎负荷计算得到：

Dlij=μlpijFzij

(9)

假设轮胎侧偏角较小，忽略车辆的轮距，得到如下的侧偏角计算式：

(10)

(11)

1.4 模型参数

表1是根据某一辆运动型多功能车(SUV)选择的预测模型参数。

表1 预测模型主要参数

符号含义数值m车辆质量/kg1 962IZ横摆转动惯量/(kg·m2)3 382lF质心到前轴的距离/m1.10lR质心到后轴的距离/m1.57d轮距/ m1.62KF前悬架侧倾刚度/(kN·m·rad-1)60KR后悬架侧倾刚度/(kN·m·rad-1)50

2 车辆稳定性控制器

NMPC车辆稳定性控制器的设计是根据第2节中的车辆动力学模型，由代价函数和约束条件构成的最优控制问题。

2.1 代价函数

代价函数V被定义为预测范围内的最优性标准的积分。具体来说，由稳定性控制器施加的纵向轮胎力分布应使得与以下参考目标的加权偏差最小：

1) 车辆的牵引力或者制动力Fx,ref；

2) 车辆的直接横摆力矩Mz,ref，即车辆左侧和右侧之间的纵向轮胎力差产生的参考横摆力矩；

3) 制动比bref，即车辆的前纵向轮胎力和总纵向轮胎力之间的比值；

预测范围是当前时间tk和末端时间tf=tk+tsNp之间的间隔，由预测步长Np和离散采样时间ts定义。纵向轮胎力是预测模型的控制输入，可以在预测范围内变化Nc次，其中Nc是控制步长，上述变量从tk+ts(Nc-1)保持不变直到tf，有如下公式：

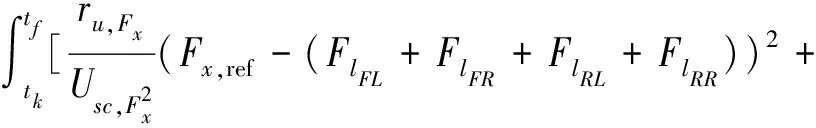
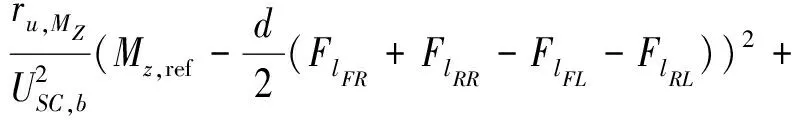
(12)

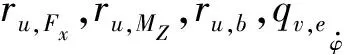
2.2 参考目标生成

Fx,ref可由车辆的期望减速度αx,ref获得，αx,ref根据油门和制动踏板上的驾驶员输入以及车辆的运动状况计算得到，则有如下公式：

Fx,ref=mαx,ref

(13)

参考横摆力矩的计算式如下：

(14)

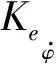
对于受控车辆的期望操纵，假设车辆速度和转向角在预测范围内是恒定的，考虑具有与重力相关梯度Kus的线性不足转向特性，可得式(15)。

(15)

(16)

为了在线性和最大横摆角速度之间实现平滑过渡，使用具有调节参数Cm和Ck的S形函数来产生参考横摆角速度，如式(17)所示。

(17)

2.3 约束条件

(18)

-αR,max-NαR(t)≤αR≤αR,max+NαR(t)

(19)

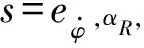
(20)

NαR(t)≥0

(21)

2.4 最优控制设置

表2为本文最优控制问题的参数设置。

表2 最优控制的参数设置

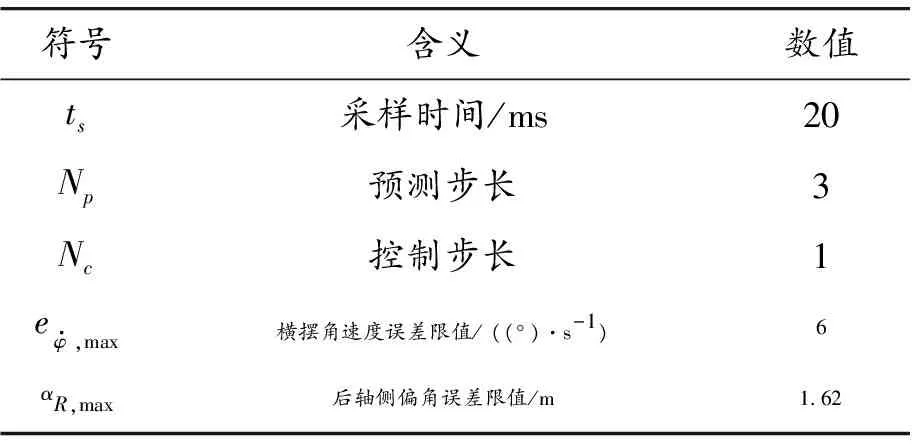
符号含义数值ts采样时间/ms20Np预测步长 3Nc控制步长 1eφ·,max横摆角速度误差限值/ ((°)·s-1)6αR,max后轴侧偏角误差限值/m1.62

2.5 多参数非线性问题

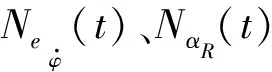
通过对连续代价函数和约束条件进行有限参数化和离散化，得到如下的优化问题：

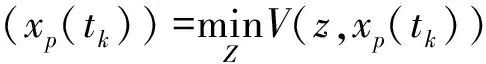
(22)

约束条件为

G(z,xp(tk))≤0

(23)

其中:参数矢量xp(tk)包含预测模型的初始状态x(tk)和缓慢变化的参数p(tk)，即xp(tk)=[β(tk),φ(tk),v(tk),δ(tk)]；优化变量Z包括输入轨迹参数U、松弛变量N和状态参数X,即有Z=[U,N,X]。

假设在tk时刻，MPC控制策略的最优解存在，记为Z*，表示预测范围内的最优开环轨迹。在电液制动系统中，纵向轮胎力Flij(tk)转化为参考液压压力。在下一时刻，利用更新后的参数向量解决优化问题，使MPC策略成为一种闭环方法。

3 显式NMPC

由于式(22)～(23)的在线解具有非线性特征，计算负载较大，很难保证实时性，因此本文提出了多参数问题的显式解。对于多参数非线性规划(mp-NLP)问题，通常不可能得到精确形式的显式解。因此，采用多参数二次规划(mp-QP)逼近mp-NLP的显式NMPC算法，得到保证次最优水平的次最优解。

3.1 MP-QP算法逼近求解

本文提出的算法是将近似mp-NLP算法与全局优化工具以及多参数二次逼近(mp-QA)算法相结合来进行求解[5-7]。

将多参数非线性规划与多参数二次规划局部逼近，得到了基于正交分区的局部mp-QP子问题的近似解。通过参数空间的迭代递归划分来控制近似精度。为了提高局部mp-QP近似的精度，并在代价、解决方法和超过最大约束的次优界方面满足误差和精度要求，采用基于参数空间部分的启发式分割规则对分区进行了细化。

对于具有mp-QP问题的mp-NLP的局部逼近是由式(22)中的代价函数V的2阶泰勒级数展开和式(23)中约束函数G的1阶泰勒级数展开得到的。

由此可以得到mp-NLP(22)-(23)的显式近似解，包括每个正交分区上mp-QP子问题的解。mp-QP子问题的解由分段仿射函数和相应的多面体临界区域组成。因此，主要的计算工作是离线进行的。在线计算简化了对给定参数向量xp的多面体区域的识别和相关的多变量仿射反馈律的计算[8]。

3.2 在线评估

实际评估过程主要分为3个阶段：

1) 对于给定的参数xp(tk)，第1层通过遍历内存优化的二叉搜索树来标识相应的正交分区和相关的局部mp-QP子问题。

2) 在确定正交分区后，第2层通过遍历二叉搜索树或顺序搜索数据结构，确定仿射状态反馈律的相应多面体临界区域。该层评估反馈律，并返回值。

3) 在最后一层中，进行可行性检查，在不可行的情况下，提供前一个时间步骤中的控制措施。

4 仿真结果

4.1 受控和非受控车辆比较

采用显式的基于NMPC的稳定性控制器，对车辆的性能进行了仿真，测试运行根据UN/ECE-R13H规则完成[9]。通过对某款运动型多功能车的仿真试验来验证控制器的有效性。

图2显示了基于NMPC的显式稳定性控制器(用实线表示)与被动车辆的响应，即无稳定控制器的车辆(用虚线表示)。被动车辆后轴侧偏角在仿真结束时增长到大约30°(在图的标尺之外)，表明被动车辆可控性受到损害。

与被动车辆相比，受控车辆的后轴侧偏角和横摆角速度具有合适的数值，后轴侧偏角处于约束范围内，避免了车辆因后轴侧滑而发生甩尾，并且车速的最终值高于被动车辆，表明所提出的控制器可以改善车辆稳定性。

4.2 代价函数中权重的影响

代价函数中权重的选择会对横摆角速度误差和后轴侧偏角误差产生较大的影响，为了进行深入分析，本文设定了3种不同的权重方案。

方案1 优先考虑后轴侧偏角的影响，对横摆角速度权值选取一定的数值。

方案2 将后轴侧偏角设为0，横摆角速度的数值与方案1保持一致。

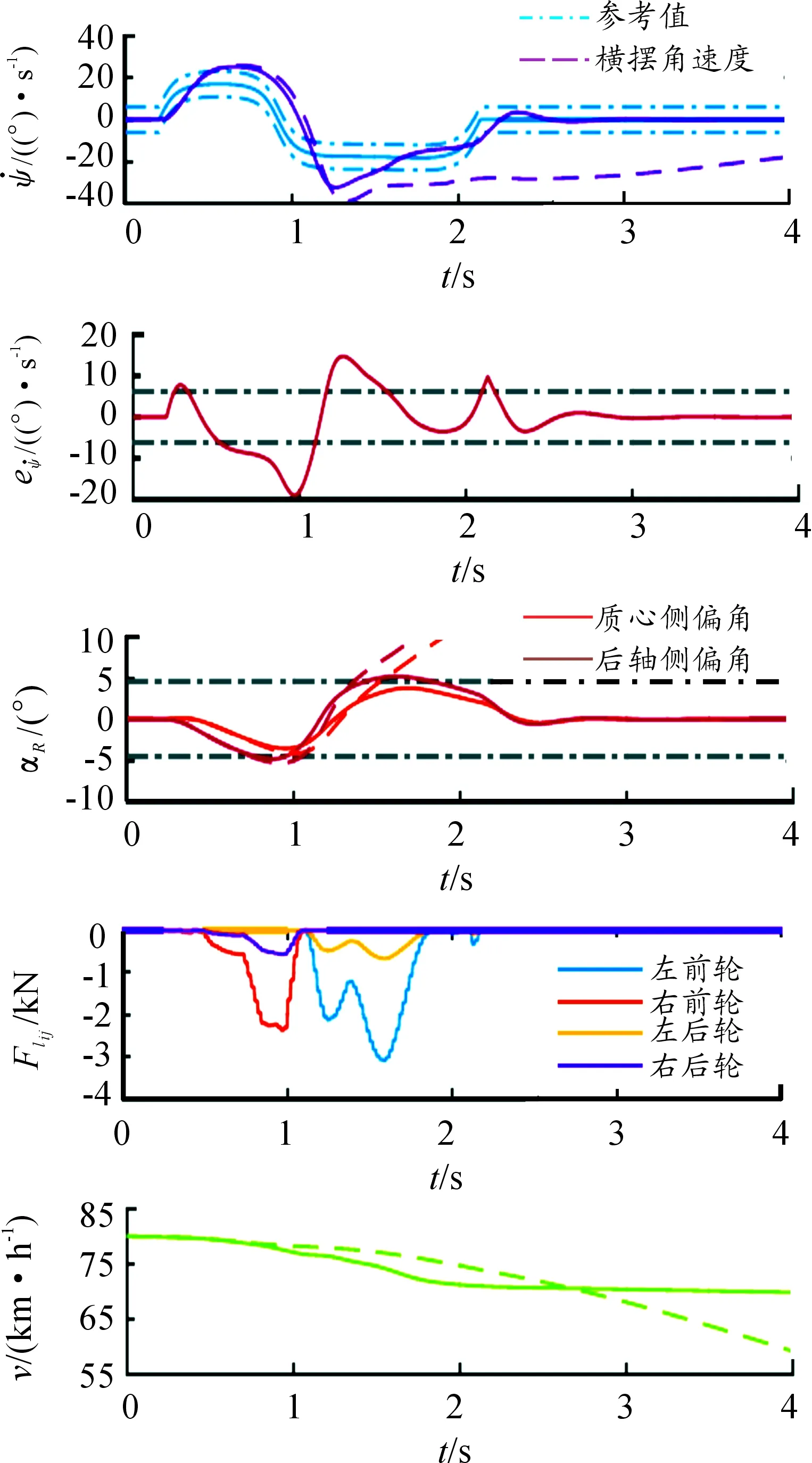
图2 显式NMPC和被动车辆的响应

方案3 后轴滑移率设为0，横摆角速度的权值相对于 1)增加3倍。

引入性能指标式(24)～(27)，通过控制器来量化权值对车辆稳定性的影响。

(24)

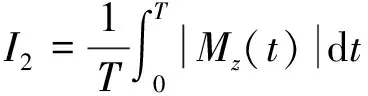
(25)

(26)

(27)

指标I1和I2分别为在仿真区间[0,T]上的直接横摆力矩MZ绝对值的最大值和平均值。指标I3和I4是由各自的松弛变量所描述的后轴侧偏角和横摆角速度误差的绝对值的平均值。

图3表示的是根据文献[11]定义的19次试运行的性能指标结果，以最大方向盘角度δsw,max=38.7°开始，增加到最终测试运行的δsw,max=270.9°。

尽管具有相同的横摆角速度误差，但是与方案1相比，方案2产生的横摆角速度误差的平均值更大，并且由于后轴侧偏角权值为零，I3的数值也变得更高。

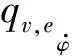
由此可以看出，在最优控制问题公式中加入相对较大权值的后轴侧偏角约束，会导致直接横摆力矩的最大值较小，同时，横摆角速度跟踪性能不受影响。

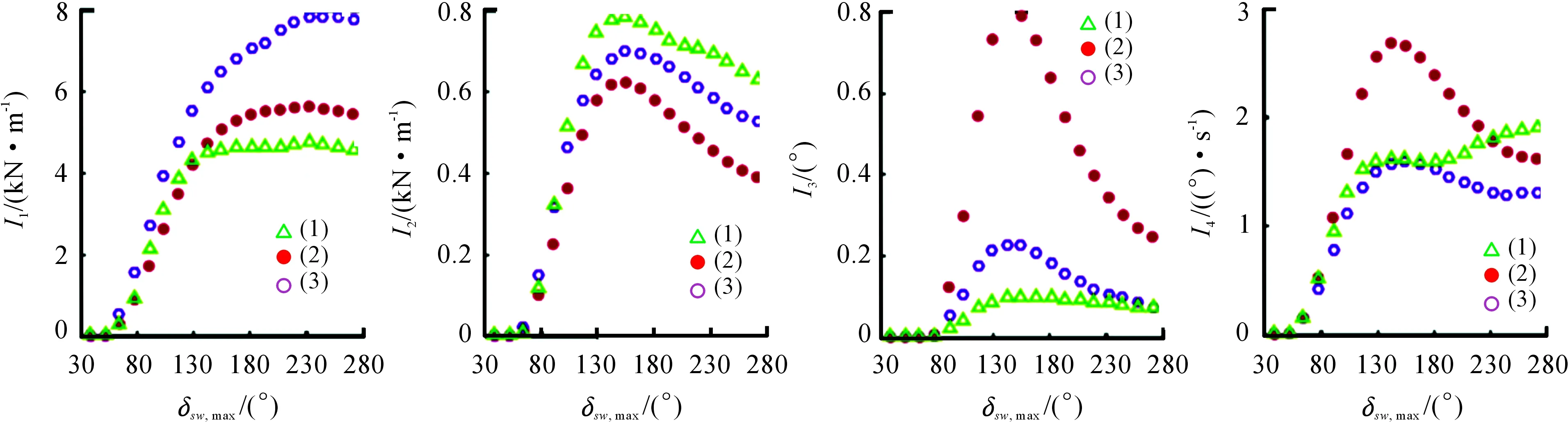
图3 不同权重对性能指标的影响

5 结束语

本文针对车辆的稳定性控制问题，提出了一种用于电动液压制动系统车辆横摆和横向稳定控制的显式NMPC算法，并进行了仿真试验和权重影响分析。仿真结果表明，显式NMPC方法可以显著改善车辆的稳定性。通过对不同权重设置的分析，说明了后轴侧偏角约束的引入对控制器性能的影响及重要性。