基于特征提取与LM-BP神经网络协同作用的异常条形码辨识方法
王永超,段志尚,王 璐,王 健,邢玉东,刘洪亮,黄大荣
(1.国网新疆电力有限公司 电力科学研究院, 乌鲁木齐 830011;2.北京南瑞捷鸿科技有限公司, 北京 100093;3.重庆交通大学 信息科学与工程学院, 重庆 400074)
近年来,随着计量生产自动化系统在电能计量器具检定和仓储作业中的广泛应用,从根本上改变了传统的人工作业方式,大幅降低了人工成本,提升了工作效率。其中,条形码作为生产自动化系统的组成部分,在电能表生产线的中转、出入库操作中起着基础、关键的作用。然而,随着周转箱在生产流水线和中转流水线中的长期使用,造成箱体条形码逐渐出现褪色、破损、浸渍等现象,使得激光扫描设备无法有效地对条形码进行识别,进而影响到生产流水线的正常运转。因此,如何对异常条形码实现准确的辨识,快速替换异常条形码,成为解决实际生产需求的重要基础性问题。
针对图像的辨识问题,国内外学者分别从特征提取、数理统计、神经网络等角度开展了相关研究,取得了一系列研究成果。图像纹理作为图像的重要特征,在计算机视觉、图像处理、图像分析等领域具有广泛的研究和应用[1-3]。因此,已有研究者从图像纹理入手开展研究。例如,陈强等[4]为解决合成孔径声呐图像的分类问题,针对图像具有不同的统计和纹理特征,以灰度直方图的标准差、峰值、灰度共生矩阵能量、熵值等作为SVM的训练特征,构造分类器,实验结果表明,该方法可有效对图像进行区域分割。赵泉华等[5]为解决传统单一特征无法实现文理图像分割精度的要求,基于像素灰度的空间相关性和不同的子区域划分,通过分别定义多个特征图像的同质区域之间的异质性势能函数和刻画各子区域领域关系势能函数定义全局势能函数,从而建立纹理分割模型,取得了较单一特征更好的分割结果。
近年来,随着神经网络技术的进一步发展,神经网络以其优异的特征学习能力,在信号处理、计算机视觉、自然语言处理等领域取得了广泛的应用[6-7]。陈燕芹等[8]基于灰度共生矩阵对图像纹理的参数进行了分析,提出了基于BP神经网络的图像复杂度评价方法,为图像的复杂度研究提供了新的研究思路。田秋红等[9]为解决一维条形码和二维条形码在识别过程中存在图像失真的问题,基于图像的不变矩特征向量建立BP神经网络的输入参数,实现了存在旋转、平移和缩放等几何失真条件下条形码的正确识别,实验结果表明:该方法具有良好的训练速度和分类能力。Singh等[10]基于随机森林分类器和决策树,构建了一个新的图像分类和检索模型。实验结果表明,该模型具有更好的搜索能力。李军锋等[11]针对图像的分类问题,提出了一种基于卷积神经网络和随机森林的识别算法,取得了较单一算法更好的识别精度。遗憾的是,该方法在训练样本量不足时识别性能不佳。黄旭等[12]为解决传统卷积神经网络特征缺少而导致图像识别过程中性能不佳的问题,采用融合线性判别损失函数的思想,对图像中的深度特征进行提取,以提高图像的识别性能。
随着电能设备生产流水线的更快速、高效的发展要求,生产流水线中的异常条形码给计量生产自动化系统带来了严峻挑战。上述研究成果,虽然从不同的图像处理角度对图像进行了分类、筛选,但仍存在模型复杂、样本要求高、单次辨识时间长等不同程度的问题,难以满足生产现场实时响应的需求。因此,以生产需求为导向,构建新的辨识模型及算法变得尤为迫切。
鉴于此,为有效解决复杂工业环境下电力设备生产流水线条异常状态的辨识问题,提出了基于多特征提取与LM-BP神经网络协同作用的辨识方法。根据生产现场异常(褪色、破损、浸渍等)和正常条形码建立特征训练库,基于LM-BP神经网络构建训练辨识模型,以实现异常条形码的智能、快速辨识。
1 条形码图像特征表征方法
1.1 自相关纹理粗糙度特征
条形码在长期周转使用的过程中,因摩擦、浸渍等造成表面粗糙度改变。已有文献表明,纹理粗糙度的大小与局部结构的空间重复周期有关,周期大的纹理粗,周期小的纹理细[13-14]。对于含有重复纹理模式的图像,当纹理粗糙时,自相关函数缓慢下降,而细纹理下降迅速。因此,自相关函数被用来测量纹理的周期性以及纹理基元的大小。设图像为f(i,j),则自相关函数定义如下:
(1)
1.2 纹理不变矩特征
图像的大小、形心等关键特征与图像的矩有关。中心矩、原点矩能较好地表征图像纹理特征,但缺乏不变性。文献[15]利用中心矩、原点矩构造出的不变矩针对旋转和缩放变化具有良好的不变性和抗干扰性,并能有效反映图像的本质特性[16]。因此,不变矩作为图像的一种重要特征,在图像处理中具有广泛的应用,本文通过对图像的7个不变矩特征进行提取来表征图像纹理。
以灰度函数f(x,y)表示m×n二维离散图像,则图像的p+q阶区域的中心矩定义如式(2)所示。
(2)
对中心距进行归一化后得到式(3)。
(3)
则7个不变矩公式为:
φ1=η20+η02
(4)
(5)
φ3=(η30-3η12)2+(η03+3η21)2
(6)
φ4=(η30+η12)2+(η03+η21)2
(7)
φ5=(η30-3η12)(η03+η21)·
[(η30+η12)2-3(η03+η21)2]+
(3η21-η03)(η03+η21)·
[3(η30+η12)2-(η03+η21)2]
(8)
φ6=(η20-η02)[(η30+η12)2-
(η03+η21)2]+4η11(η30+η12)·
(η03+η21)
(9)
φ7=(3η21-η03)(η30+η12)·
[(η30+η12)2-3(η03+η21)2]+
(3η12-η30)(η03+η21)·
[3(η30+η12)2-(η03+η21)2]
(10)
1.3 曲线特征
正常条形码在对图像进行边缘检测后二值化图像中边缘规则、光滑、连续,数量容易辨识;异常条形码边缘相对散乱,存在不同程度的断开、混乱现象,如图1 所示。因此,可用图像中边缘直线数对图像磨损进行表征。

图1 正常和异常条形码曲线特征对比
1.4 HOG方向梯度直方图
HOG(histogram of oriented gradient,梯度直方图特征)[17-18]作为一种对图像局部重叠区域密度进行表征的方法,广泛应用于图像的识别。HOG特征提取的步骤如下:
步骤1 对图像进行灰度化处理。
步骤2 采用Gamma校正法对输入图像进行颜色空间的标准化,用于调节图像的对比度,降低图像局部的阴影和光照变化所造成的影响。
步骤3 计算图像每个像素的梯度用于获取轮廓信息,并进一步弱化光照的干扰。
步骤4 将图像划分成若干cells,统计每个cell的梯度直方图,即可形成每个cell的descriptor;
步骤5 将若干cell组成一个block,将一个block内所有cell的特征串联起来便得到该block的HOG特征。
步骤6 将图像内的所有block的HOG特征串联起来就可以得到该图像的HOG特征。
由于正常条形码黑白区域间隔分明,纹理清晰,从竖直方向上看,每个block的HOG特征应与同一列的其他block相似,从水平方向上看,在不同block中,具有重叠cell区域的HOG特征也理应相似,如图2(a)所示,污损条形码的HOG特征则比较散乱,如图2(b)所示,所以提取水平方向上的HOG特征方差与竖直方向上重叠区域的HOG特征方差作为正常条码与污损条码的辨识依据。

图2 正常和异常条形码曲线HOG特征对比
2 基于特征提取的LM-BP神经网络条形码辨识模型
2.1 BP网络学习算法
BP神经网络作为一种经典的多层前馈神经网络模型,因其较好的泛化能力、容错能力以及算法实时性,在图像识别、故障诊断等领域取得了广泛的应用[19-23]。BP算法的基本思想是根据训练样本,利用梯度下降算法对网络模型中的结点权重进行自适应的动态调整,使得期望输出尽可能接近实际输出。传统BP神经网络结构模型如图3所示。
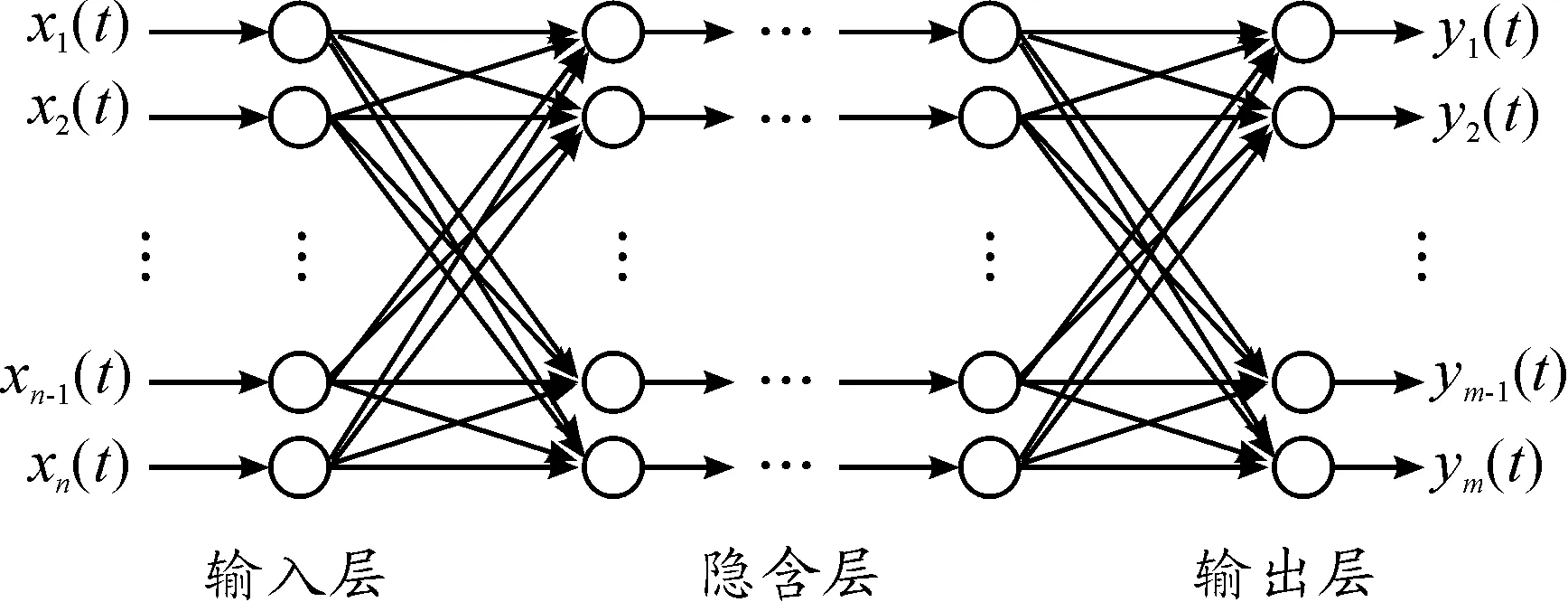
图3 多隐层BP神经网络结构模型
图3中,BP神经网络的输入为x1,x2,…,xn,BP神经网络的输出为y1,y2,…,ym,网络节点相应的权值分别为wij和wjk。从图中可以看出:BP神经网络相当于一个非线性函数,通过对样本的训练,可以反映输入到输出的映射关系。因此,BP神经网络对异常条形码进行分类预测,就是逐步迭代寻找一个非线性函数。BP神经网络训练过程如下:
步骤1 初始化神经网络参数。根据输入输出序列(x,y)确定网络输入层节点数n、隐含层l,输出层节点m,初始化输入层、隐含层和输出层神经元之间的连接权值wij、wjk,初始化隐含层阈值a,输出层阈值b,给定学习速率和神经元激励函数。
步骤2 计算隐含层输出。网络输入向量x,通过输入层和隐含层间连接权值wij以及隐含层阈值a,得到隐含层输出H。
(11)
式中:l为隐含层节点数;f为隐含层激励函数。该函数有多种表达形式,根据实际数据情况可进行选择。
步骤3 计算神经网络输出值。根据隐含层输出H,连接权值wjk和阈值b,得到神经网络预测输出O。
(12)
步骤4 计算输出值与期望值之间的误差。根据网络预测输出O和期望输出Y,得到网络预测误差e。
ek=Yk-Ok,k=1,2,…,m
(13)
步骤5 进行权值更新。根据网络预测误差e对网络中的连接权值wij和wjk进行更新。
i=1,2,…,n;j=1,2,…,l
(14)
wjk=wjk+ηHjek
j=1,2,…,l;k=1,2,…,m
(15)
式中η为学习效率。
步骤6 进行阈值更新。根据网络预测误差e对网络节点阈值a和b进行更新。
j=1,2,…,l
(16)
bk=bk+ek,k=1,2,…,m
(17)
步骤7 判断迭代误差是否小于阈值,若小于,则迭代结束;若不小于,则返回步骤2。
2.2 LM网络学习算法
BP神经网络算法作为一种广泛使用的网络模型,虽然在图像处理、故障诊断等领域取得了广泛的应用,但在实际的应用中,由于其基于梯度下降法在学习效率和稳定性上存在缺陷。因此,为改进传统BP训练算法存在的不足,研究者将LM算法引入到BP中,以提高学习的性能和稳定性[23-26]。
在LM算法中,设误差指标函数为
(18)
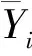
若在第k次迭代中取值和阈值构成的向量为wk,则满足:
wk+1=wk+Δw
(19)
Δw=[JT(w)J(w)+μI]-1JT(w)e(w)
(20)
式中:J(w)为Jacobian矩阵;I为单位矩阵;μ为学习率。LM训练过程主要如下:
步骤1 初始化网络参数:设定网络训练误差ε;常数μ0,β(0<β<1);初始化权重和阈值向量,令k=0,μ=μ0。
步骤2 计算网络输出和误差相应的E(wk)。
步骤3 计算Jacobian矩阵J(w)。
步骤4 计算Δw。
步骤5 若E(wk)<ε,算法结束。
步骤6 根据wk+1=wk+Δw,计算E(wk+1)。
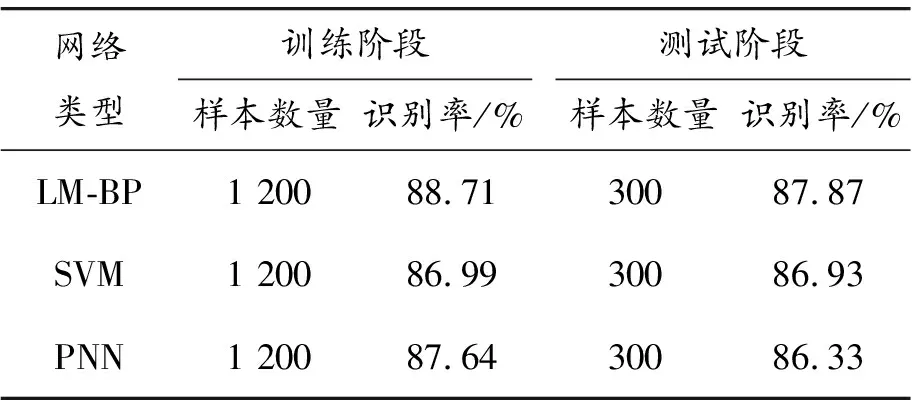
若E(wk+1) 利用LM-BP神经网络对异常条形码进行辨识时,将现场采集的图像分为2组,一组作为训练图像,一组作为测试图像。将提取后的图像HOG、曲线特性、纹理粗糙度、纹理灰度构成特征矩阵,输入BP神经网络进行训练,得到训练模型,然后利用测试特征进行测试。条形码辨识系统框图如图4所示。 图4 条形码辨识系统框图 实际生产过程中,直接的物理接触可能会导致条形码残缺、不平整、损污,影响条形码的识别进而降低生产过程中的运行效率,所以对于生产过程中由于残缺、不平整、损污等导致的无法识别的条形码进行甄别并排除显得尤为重要。以国网新疆电力有限公司电力科学研究院计量生产自动化系统现场为例。现场生产环境如图5、6所示。 图5 智能电表检定流水线 随着周转箱在生产流水线和中转流水线中的长期使用,造成箱体条形码逐渐出现条码褪色、破损、浸渍等现象,使得激光扫描设备无法有效对条形码进行识别,进而影响到生产流水线的正常运转。因此,如何对异常条形码实现准确的辨识,快速替换异常条形码,成为解决实际生产需求的重要基础性问题。 根据现场实际情况条形码在长期使用过程中存在磨损、缺失、浸渍等显现,为验证基于特征提取和LM-BP神经网络的辨识效果,模拟条形码的磨损等情况,建立特征库,典型图片如图7~10所示。 图6 智能电表中转流水线 图7 正常条形码 图8 异常条形码(磨损) 图9 异常条形码(缺失) 为验证上述方法的合理性和有效性,将条形码图像分为训练和测试的图像集,通过特征提取方法,对训练和测试图像提取主要的特征,分别构成训练特征数据集合测试特征数据集。在利用LM-BP神经网络对训练特征集进行学习时,神经网络参数如表1所示。 表1 LM-BP神经网络参数设置 根据上述基于特征提取与LM-BP网络辨识的算法模型,利用图像特征提取后的数据集进行验证。同时,为进一步反映辨识效果,采用十折交叉验证的方式,将LM-BP的辨识结果与支持向量机(support vector machine,SVM)、概率神经网络(probabilistic neural network,PNN)辨识结果进行比较,结果如表2所示。 表2 训练/测试样本集数量 根据表2,基于特征提取与LM-BP神经网络的辨识准确率均比SVM和PNN高。因此,该方法可用于异常条形码的辨识中。 本文针对工业生产环境中条形码的异常识别问题,以图像的HOG特性、曲线特征、纹理粗糙度、纹理灰度特征建立特征库。在此基础上,建立以BP神经网络为核心的训练-辨识框架。实验结果表明:本文提出的算法能有效实现对异常条形码的辨识,在训练阶段和辨识阶段平均识别率保持在88.29%左右,具有实际的应用价值。但考虑到实际工程应用的复杂性,生产流水线上的异常条形码需要更快速、高效的辨识。因此,在后续的研究中,将结合工程需求,致力于提高网络的识别速度并进一步提高准确率。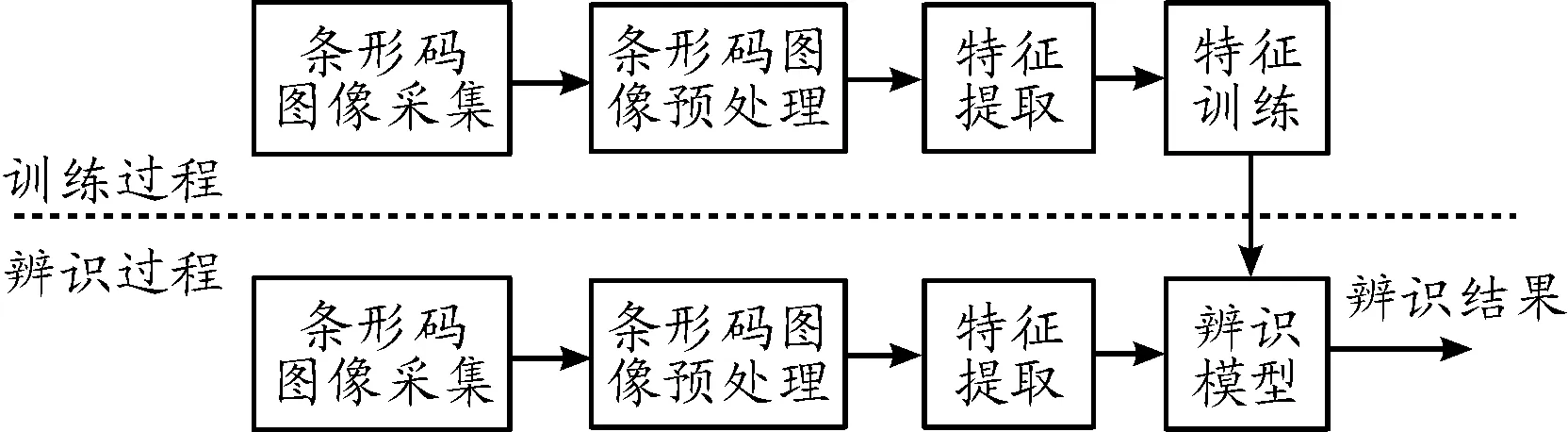
3 算例与分析






4 结束语

