Delta并联3D打印机运动学分析

杨秀芳，孙有朝，赵大旭，杨自栋，姚立健，张培培

(1.南京航空航天大学， 南京 211106； 2.浙江省竹资源与高效利用协同创新中心， 杭州 311300；3.浙江农林大学， 杭州 311300)

“3D打印(3D printing )”形象地描述了增材制造(additive manufacturing，AM)的工艺特点，这种“自下而上”的制造方法已经伴随着材料领域的发展从工业领域扩展到了家用领域。熔融沉积造型(FDM-fused deposition modeling)是一种挤压成型的3D打印技术，适合打印低熔点材料，尤其是无毒环保、可降解的材料，目前应用最广泛。针对FDM工艺的特点，目前研究主要集中于开发新材料和提高打印精度和质量[1]。其中，机械结构本体，即打印机构问题是提高打印精度和质量的关键。

串联构型的3D打印机发展比较成熟，若要继续提高潜力，需要从机构学角度研究更加适合FDM工艺的打印执行机构。基于上述思路，并联机构在3D打印中的应用逐渐引起重视。李江滨[2]以3D打印机机械本体—3-P[2-SS]并联机构为研究对象，对该机构进行了运动学分析、运动学标定、误差建模，并设计制作样机进行了实验研究。曲兴田等[3]设计出一种工作平台可翻转的3D打印机，完成无支撑结构的曲面结构打印。周辉等[4]提出一种完全解耦五自由度混联机构作为3D打印的执行机构。薛国芳[5]提出了一种基于 3-PUU 型三自由度 3D 打印并联机器人，该并联机构具有较好的运动学和动力学性能。

本文基于Delta机构设计了一种3-PUU构型并联3D打印机,在RecurDyn环境下进行了轨迹优化和仿真试验，验证了设计的合理性。

1 打印机构构型方案

1.1 适用构型

并联机构结构紧凑、刚度大、承载能力强，而且运动惯性小、驱动误差小、位置精度高和各向同性好[2]。随着相关理论研究的不断深入以及工程应用实践探索，并联机构先后被成功应用于诸多领域，如并联运动学机床、并联机器人、定位装置、测量装置、飞行模拟器、医疗、娱乐等。虽然并联机构存在其特有的缺点，比如工作空间小、存在奇异问题等，但是其能更好地满足微细加工工艺对精度的需求，与打印机构功能需求吻合[6-7]。

由于FDM工艺中，喷头喷出后冷却的固化层面与喷嘴垂直，当完成一层的喷涂时打印头继续按设定的零件截面轮廓和填充轨迹运动，同时将熔融状态下的材料挤出，前一层的材料粘结并固化。因此，喷头的主运动是三维空间中的平动，如图1所示。

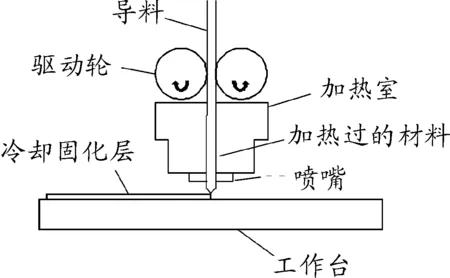
图1 喷头工作原理图

典型并联机构，如Stewart平台及其变型，大都具有6个自由度，运动控制复杂度较高，而对于多数3D打印机，少自由度并联机构则更适合。相比而言，少自由度并联机构有下列优点：① 驱动件减少，构件少；② 工作空间大；③ 运动耦合较弱，容易解耦；④ 控制简单方便；⑤ 制造容易，价格低廉；⑥ 正向求解简单[8-9]。

1.2 构型选择

目前，大多数并联打印机构都选择了较为成熟的Delta并联机构及其演化机构。Delta机构刚度大、响应灵敏，具有优异的综合性能，并且无误差积累，适合用于打印机构，国内外研究相对丰富。国内一些高校在并联机构应用于3D打印机的研究中取得了若干成果，燕山大学则研究了用于3D打印的3-CUR 解耦并联机构[10]，北京交通大学潘英基于3T1R和3T2R构型设计了打印机，并分析了其运动学性能[11]。本文在前期用于3D打印的竹塑复合材料研究基础上[12]，基于Delta构型设计了打印机构，分析了机构运动学性能，对典型打印过程进行了运动学分析。

2 运动学分析

2.1 构型描述与自由度

提取旋转关节的中心点，将Delta并联机构简化为静平台、动平台以及连接它们的3条对称分布的运动支链。

假设静平台和动平台铰接点的外接圆半径分别为RS和RT，在静平台中心点O建立全局坐标系O-x、y、z，静平台3个铰接点Am0(m=1,2,3)向中心点O平移1个动平台外接圆半径，将动平台简化为一点P，建立工具坐标系P-xp、yp、zp，如图2所示。用Am(m=1,2,3)标记静平台顶点，OAm=l1=RS-RT，与OX的夹角为αm，主动臂与静平台的夹角为βm，连杆相对主动臂的夹角为γm，AmBm=l2，PBm=l3分别为主动臂和连杆的长度。

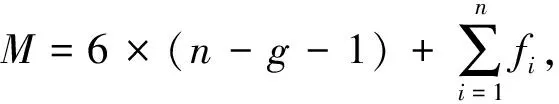
2.2 位置逆解

运动学逆解是根据已知的末端执行器P的位置矢量r，求解节变量β=[β1,β2,β3]T及其对时间的1阶和2阶导数。由图2中位置关系可知：

r=[x,y,z]T=l1im+l2jm+l3km

(1)

式中im,，jm，km分别表示OAm、AmBm与PBm的单位矢量，其中im=[cosαm, sinαm,0]T，jm=[cosαmcosβm, sinαmcosβm,-sinβm]T，km待定。由式(1)得：

l3km=r-l1im-l2jm→(l3km)(l3km)T=

(r-l1im-l2jm)(r-l1im-l2jm)T→

(2)

从而消去km，式(2)展开并整理，可得位置反解βm：

(3)

系数Mm、Nm与Qm分别为：

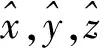
(4)

2.3 速度与加速度逆解

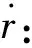
(5)

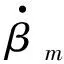
(6)

式(6)描述了主动臂关节速度与动平台速度之间的映射关系，定义间接Jacobi矩阵JI与直接Jacobi矩阵JD[14]：

(7)

则可将式(6)表示为矩阵形式：

(8)

显然，Jacobi矩阵J反映了末端执行器的速度与主动关节速度之间的映射关系。加速度推导过程和速度逆解类似，式(8)对时间求导可得加速度逆解：

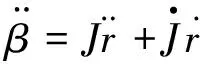
(9)

2.4 运动学正解

运动学正解是给定主动臂关节变量β，求解末端执行器P的位置矢量r，根据构型可知，Bm点在以P为圆心、l3为半径的球面上。式(2)在消去km时给出了各运动支链对应的球面方程：

(10)

上述3个方程求解可得到2个位置正解，舍去存在机构干涉的解，得到P点位置矢量r。

(11)

3 工作空间与尺度综合

3.1 基于几何法的工作空间分析

Delta机构的工作空间，是该机构动平台能伸展的最大空间，即动平台的轨迹能达到的最大范围。工作空间的大小某种程度上决定了机构的性能，从而决定该3D打印机的性能。另外，工作空间也对机构的尺寸具有一定的约束，在尺寸的优化上起到关键性的作用。

工作空间可采用Monte Carlo数值积分法和几何法求得。本文选用几何分析法，通过两两圆弧相交可以获得具体的几何形状，再通过求解几何算式来求得工作空间[15]。

主动臂处于极限位置(βm=βmin和βm=βmax)时，连杆l3摆动至极限位置，生成可达空间的边界，如图3所示，而工作空间(灵活空间)是一个包含在边界内的半径R、高H的圆柱体，该圆柱体上端面距离驱动臂βm=0时高度为h，长度为2R。通过几何分析[16]，获得以下方程：

(12)

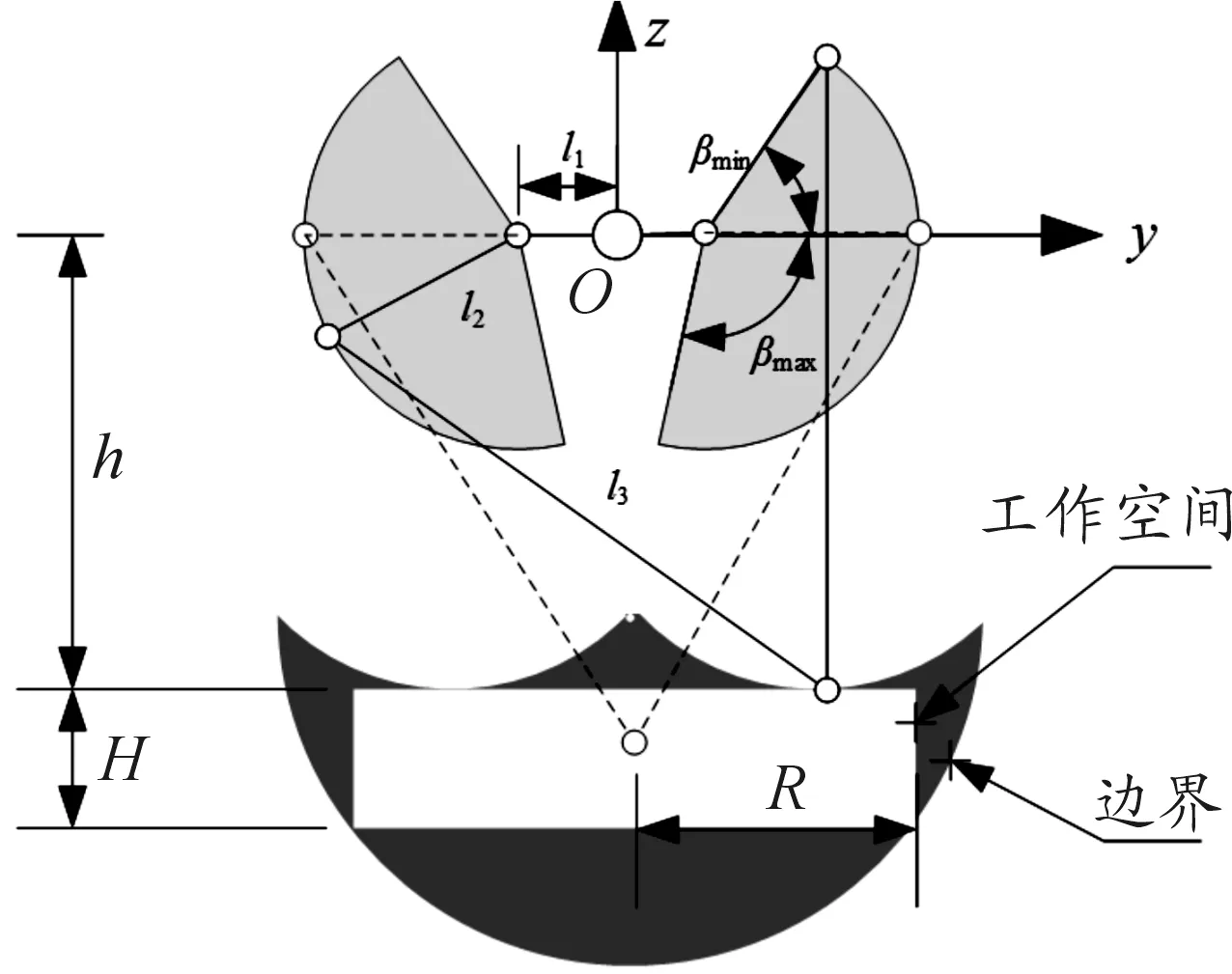
图3 Delta机构工作空间平面简图

末端执行器的位置坐标约束在圆柱体内的工作空间中，z轴上的高度满足条件h≤z≤h+H。为了使打印机在作业时能够充分获取工作空间的每一点并利用，可以使半径R的实际值Rn在一定范围内浮动，即R≤Rn≤1.1R，最后要求解出半径R与机构的几何尺寸的关系。根据并联机构与作业工作空间的几何关系得：

(l2cosβmax+l2)

(13)

3.2 构型尺寸综合

本设计思路是在给出该并联机构工作空间的这些参数即高度H、距离h、半径R的情况下，进行机构本体几何尺寸参数l1(RS-RT)，l2，l3，αm以及主动臂摆角βmin和βmax的确定。

1) 直接Jacobi矩阵JD中任意2个及以上分量km(m=1,2,3)线性相关，即2个及以上连杆平行或共面；

2) 间接Jacobi矩阵JI中出现jm×km=0(m=1,2,3)时，即同一个运动支链中，主动臂与连杆平行。

为了让机构极大程度地避免出现奇异位形的情况，主动臂摆角βmin和βmax需要限定范围，βmax根据几何尺寸确定，而βmin≥arcsin(l2-h/l1)。初步确定尺寸参数如表1所示。

表2 尺寸参数

3.3 正反解验证

已知RS=120 mm，RT=60 mm，l2=200 mm，l3=550 mm， 给定动平台P的3组坐标，用Matlab程序求机构运动学反解的解。给出的3组坐标分别为(-300,300,500) (300,-300,500) (0,300,500)。

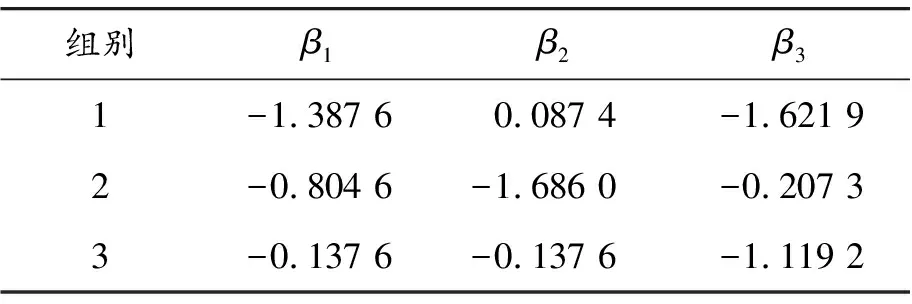
表3 运动学反解结果

将上述3组解代入Matlab的运动学正解计算公式中，可以求得P的3组坐标(300.010 7, 299.968 9, -500.016 5)(299.992 7, -299.992 1, -500.014 6)(-0,300.019 8, -499.985 4)。将z坐标的数正数化，圆整3组坐标后可以发现与给定的坐标是相符合的。

综上可知，该机构的运动学正反解分析验证成功。

3.4 打印精度分析

影响3D打印精度的因素主要是机械本体结构与打印工艺的误差，其中前者尤为关键。Delta并联机构只有3个平移自由度，因此只有位置误差是可以通过控制策略进行补偿的，而姿态误差只能通过提高制造和装配的精度来减小。

忽略各驱动臂和各连杆的尺寸差异，将动平台参考点P的位置(x,y,z)定义为3个主动臂关节变量β=[β1,β2,β3]T和l1、l2、l3的函数[8]：

(14)

将式(14)的全微分分解为控制参数与结构参数误差两部分，得到正解误差模型：

(15)

将式(15)简写为：

dr=TAdβ+TCdL

(16)

其中：dr为动平台输出误差；TA与TC分别为驱动参数误差与构件制造误差的传递矩阵； dβ与dL分别为驱动参数误差与机构参数误差。位置的逆解误差模型可由式(16)变形得到：

(17)

4 基于RecurDyn的仿真

4.1 打印轨迹设定

在RecurDyn中导入各构件的X_T模型，通过约束“装配”运动模型，利用Cmotion(G)定义打印机喷头运动，由于打印机构只存在3个平动自由度，所以忽略关于姿态的定义RX、RY、RZ，只需设置X、Y、Z轴方向运动。课题组根据前期材料性能试验，做了各种轨迹和参数的仿真，为直观描述打印机构运动学性能，定义螺旋运动：

(18)

即：喷头在初始位置(0, 0,z0)首先沿X轴方向以速度vx移动t0，然后以vxt0为半径做空间螺旋运动，λ为螺旋运动的导程，轨迹如图4所示。

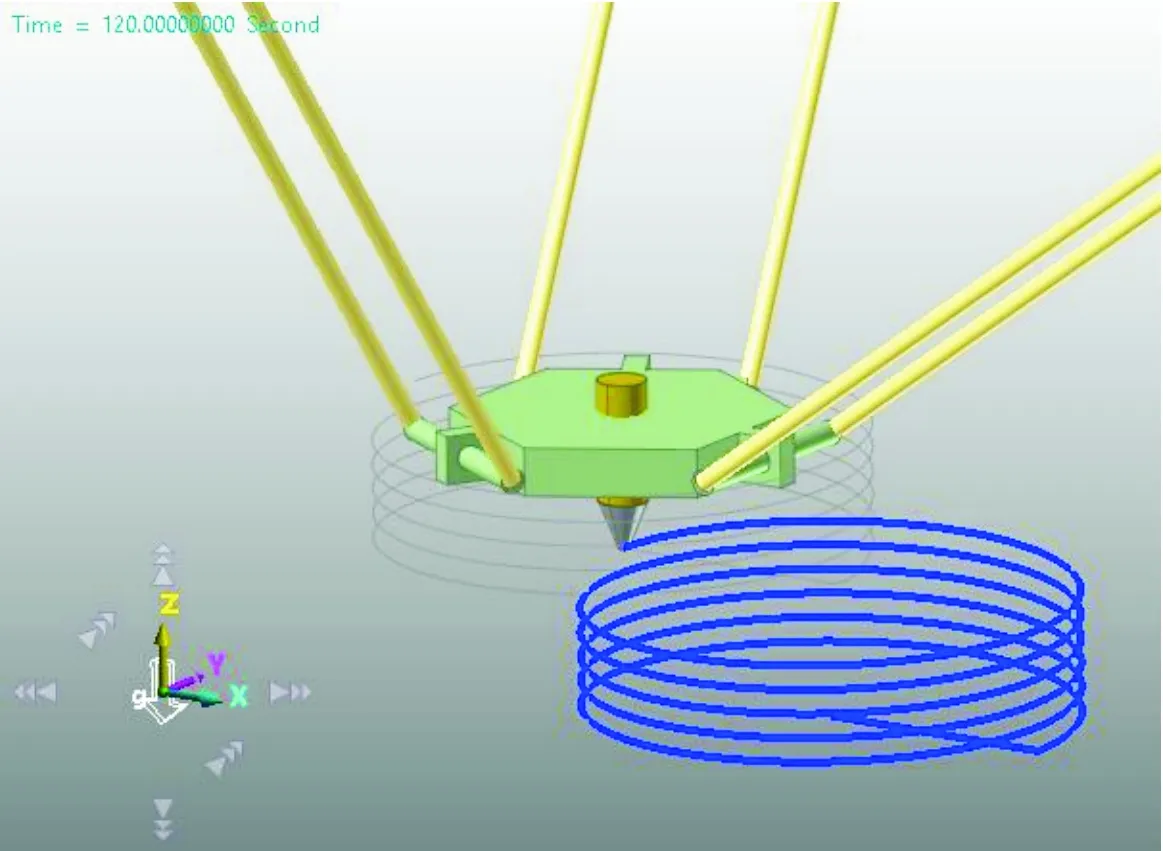
图4 打印轨迹

式(18)各参数可根据实际工艺过程定义。仿真时长和步数确定后，运行仿真就可以输出相应结果。

4.2 运动学仿真分析

选择初始参数如表4所示。

表4 初始参数

利用RecurDyn中的IF函数描述式(18)，在直线运动与螺旋运动转换时，出现加速度突变，为避免出现刚性冲击，改用STEP5函数描述式(18)，仿真120 s，1 200步。图5～7分别是动平台的位移、速度、加速度曲线，可见无刚性冲击出现。

由动平台运动参数可以解算出驱动副，即3个主动臂的主动关节运动参数，这些参数作为实现期望打印轨迹的控制变量。图8所示为主动臂关节角变化曲线。

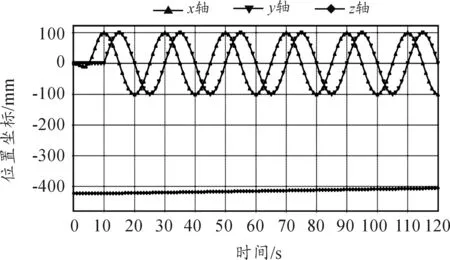
图5 动平台位置

图6 动平台速度

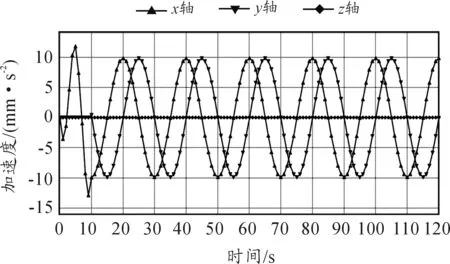
图7 动平台加速度

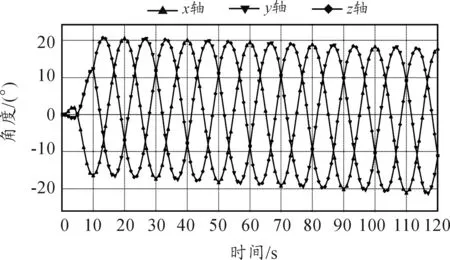
图8 主动臂关节角

图9则是主动臂关节角速度变化曲线，同样是光滑无刚性冲击，反映了与动平台之间的映射关系。

图9 主动臂关节角速度

图10为主动臂关节角加速度变化曲线，在整个打印过程中，可以平滑无突变地过渡，与期望的基本一致。

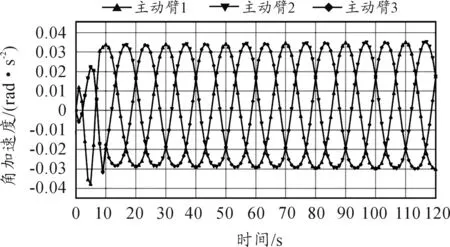
图10 主动臂关节角加速度

由仿真情况可知，在打印过程中喷头的运动能够无突变地过渡，在合理范围内。

5 结束语

1) 针对基于Delta并联机构的3D打印机，构建了基于向量运算的具有简洁直观形式的运动学模型，分析了动平台与主动臂之间的位置、速度和加速度映射关系，并进行了正反运动学的验证。

2) 利用虚拟样机技术，对所设计3-PUU构型并联3D打印机进行了规划路径运动学分析，直接得到分析结果，与繁琐的符号运算实现了互补，为样机开发提供了一种有效方便的分析方法。

3) 优化了构型尺寸参数，利用5次多项式插值方法优化了打印轨迹，避免了出现刚性冲击。