基于MEA-BP神经网络的压气机特性曲线预测

黄 伟,常 俊,孙智滨

(上海电力学院 自动化工程学院， 上海 200090)

燃气轮机是一种重要的动力机械，被广泛应用于航空航天、轮船舰艇和火力发电等多个领域。针对燃气轮机核心技术需要长期从国外进口的情况，燃机技术国产化势在必行。采用模块化建模的方式对燃气轮机建立整体模型，可以得到相关的建模数据，进而可以进行故障诊断、健康管理和状态监控等研究。可见，对燃气轮机进行建模仿真并研究其性能特点具有很高的实用价值[1-2]。

在燃气轮机的整体建模仿真中，压气机作为一个重要的组成部分，其流量和效率特性曲线的准确性直接关系到发电机稳态、瞬态过程模拟以及发电机与增压器匹配计算的精度。但是，由于压气机特性曲线的可变性和离散不连续的特点，对该曲线的预测成为建模的重点和难点。因此，要根据有限的样本数据，借助合适的建模方法对压气机特性曲线进行预测，得出变工况条件下不同转速所对应的流量和效率，进而为后期燃气轮机的整体建模打下基础。

压气机的特性曲线基本都是在额定工况下通过试验的方法得到的，变工况的情况下，试验测得的数据更加离散化，不利于后期的统计与分析。崔茂佩[3]通过人为划分依据线，确定等转速线的拟合区域，利用二步一元方法分别拟合；张东阳[4]利用插值函数法和最小二乘法对压气机特性曲线做第一步和第二步拟合，并对不同拟合幂次所得结果进行比较。目前大多方法都存在泛化能力不足的特点。

思维进化算法(mind evolutionary algorithm，MEA)作为一种改进的种群优化算法，具有全局寻优的能力，可以改善神经网络的收敛速度和精度，已被使用于疾病研究、发电机故障分析、变压器故障诊断和电厂主气温控制等多个领域[5-7]。在神经网络的权值和阈值范围内，通过MEA的多次“趋同”与“异化”操作进行全局寻优，将得到的全局最优解应用于BP神经网络的初始值中。实践证明，使用MEA优化的BP神经网络方法能够提高拟合和预测的准确性，并且具有很强的记忆功能，提升了模型的泛化能力，适合于预测不同转速下的压气机特性曲线[8]。

为了弥补BP神经网络的不足，笔者拟将MEA引入压气机特性曲线预测，采用MEA优化BP神经网络的权值和阈值，探讨MEA优化后的BP神经网络在压气机特性曲线预测模型中的精度和泛化能力，为后期燃气轮机整体模型的建立和仿真做好准备。

1 燃气轮机模型

利用Matlab/Simulink建立某重型燃气轮机整体模型，作为稳、动态仿真的框架基础。模型如图1所示。

图1所示模型为采用模块化建模搭建的燃气轮机整体模型，分为压气机模块、燃烧室模块和透平模块。压气机模块的输入参数有温度、压力、转速和压比。输出参数主要为空气流量，该输出参数在燃气轮机整体模型的分析中至关重要。通过对压气机特性曲线的处理和预测，得到非设计工况、任意转速条件下的空气流量，进而得出燃烧室的进气量，为后续燃烧室和透平的建模研究打下基础[9-11]。

为了得到满足该整体模型的压气机特性曲线预测结果，本文分别采用BP神经网络和MEA-BP神经网络进行优化，并对结果进行对比分析。

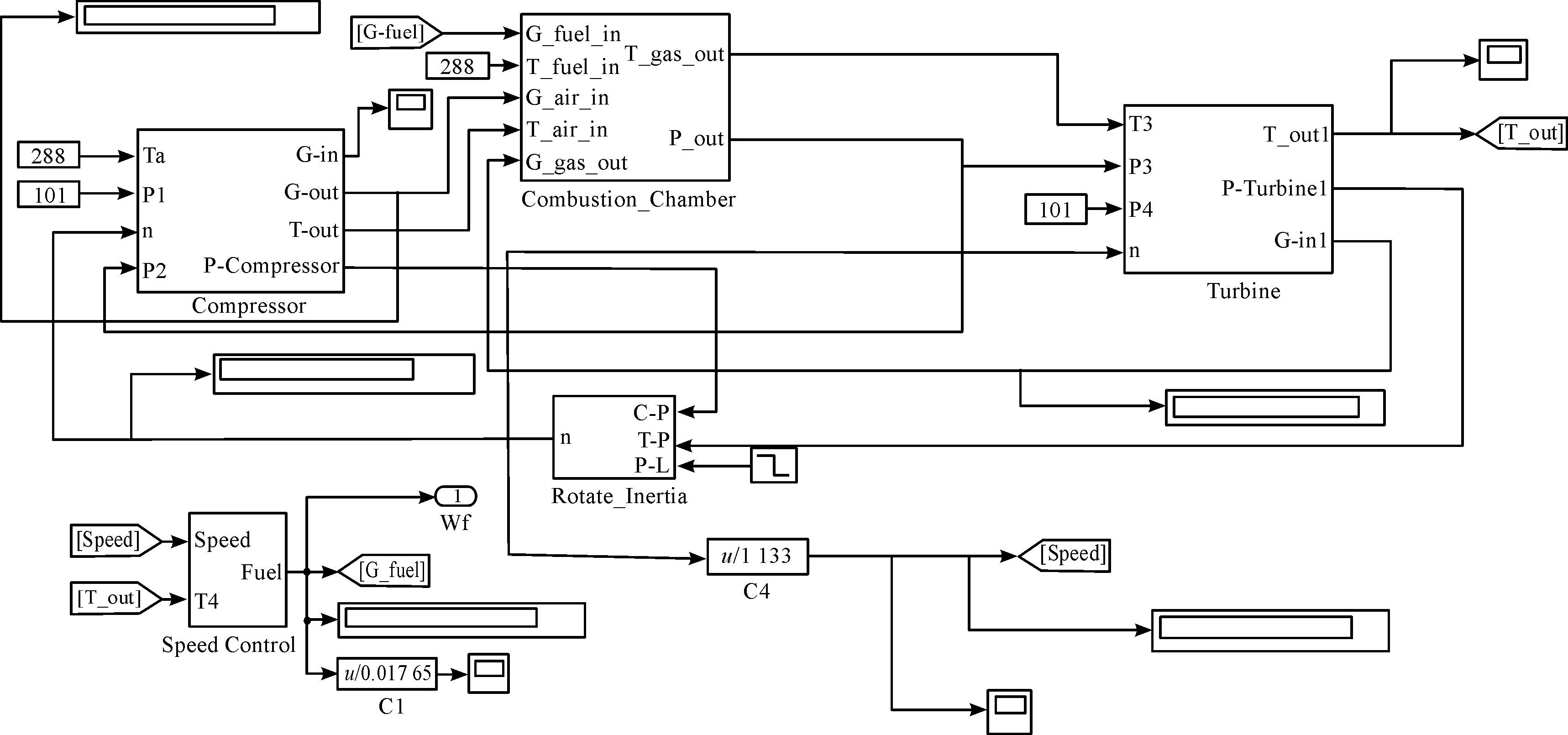
图1 某重型燃气轮机整体模型

2 MEA-BP神经网络

2.1 BP神经网络

BP神经网络是一种多层前馈神经网络模型，该网络的主要特点是信号前向传递，误差反向传播。BP神经网络采用反向传播算法作为学习算法，激活函数通常采用连续可导的S型函数，随着激活函数的不同会推算出不同的权值调整公式。如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使 BP 神经网络预测输出不断逼近期望输出。BP神经网络的网络拓扑结构如图2所示。

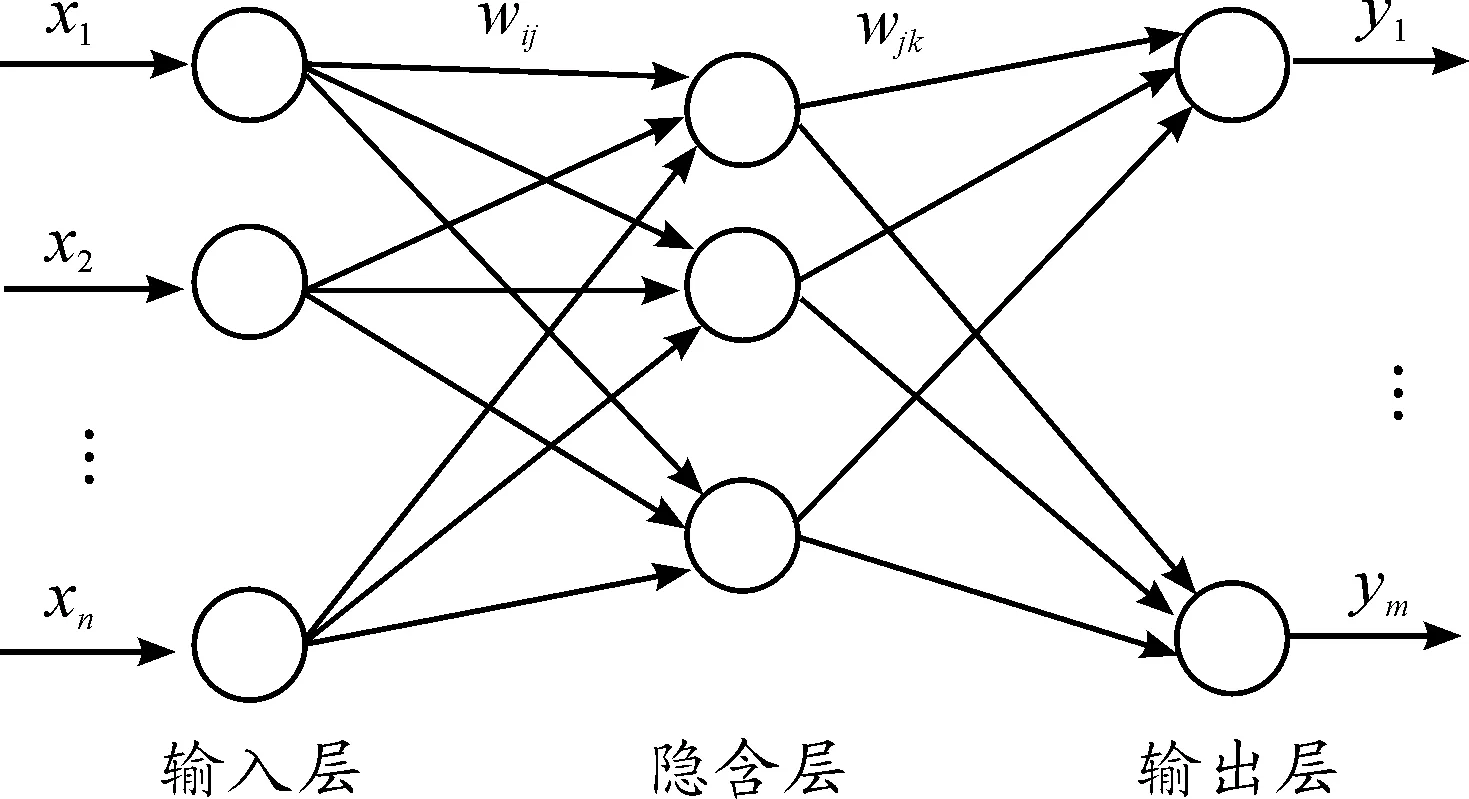
图2 BP神经网络的网络拓扑结构

由图2可知，BP神经网络可以看成是一个非线性函数，网络输入值和预测值分别为该函数的自变量和因变量[12-13]。对于3层神经网络，具体的训练过程如下：

1) 初始化网络

确定输入维数n、输出维数m和隐含层节点数l，初始化权值和阈值。

2) 计算隐含层输出

(1)

式中：f为神经元激励函数；wij为隐含层神经元间的连接权值；a为隐含层阈值。

3) 计算输出层

(2)

式中：wjk为隐含层与输出层神经元之间的连接权值；b为输出层阈值。

4) 误差计算

ek=Ok-Yk

(3)

5) 权值更新

(4)

wjk=wjk+ηHjek

(5)

6) 阈值更新

(6)

bk=bk+ek

(7)

7) 判断算法迭代是否结束；若未结束，则返回步骤2)。

2.2 MEA-BP神经网络

2.2.1 思维进化算法

思维进化算法(MEA)沿袭了遗传算法的一些基本概念，其基本框架如图3所示。

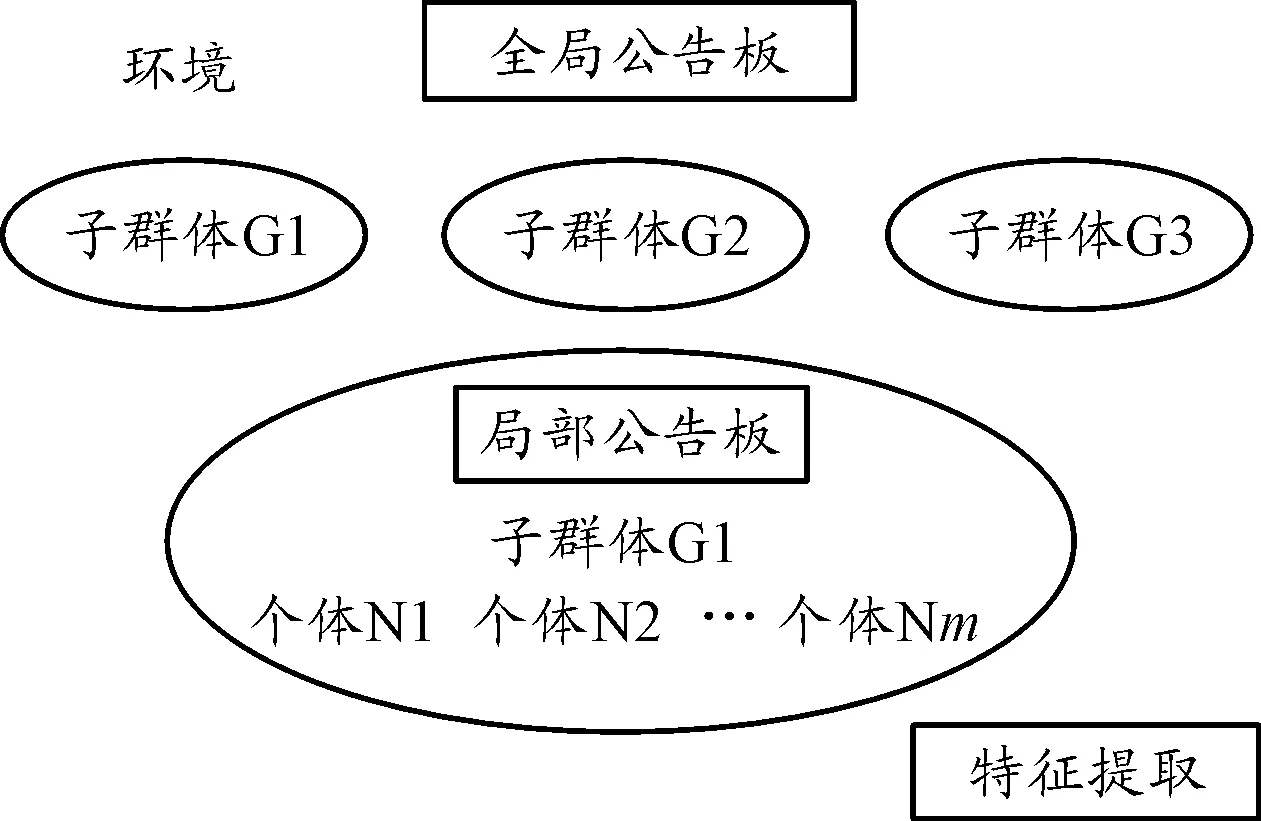
图3 思维进化算法系统结构

由图3可知，思维进化算法主要由以下4个环节组成：群体和子群体、公告板、趋同和异化。其中，趋同和异化过程是思维进化算法的核心部分，代替了遗传算法中交叉和变异这2种遗传算子，决定着该算法的精度和记忆能力。

2.2.2 MEA优化过程

思维进化算法的设计思路就是对BP神经网络的初始权值和阈值进行优化。首先，根据 BP 神经网络的拓扑结构，将解空间映射到编码空间，每个编码对应问题的一个解。然后，选取训练集的均方误差的倒数作为各个个体与种群的得分函数。利用思维进化算法，通过不断迭代，输出最优个体，并以此作为初始权值和阈值，训练BP神经网络[7-8]。其优化过程如下：

1) 根据BP神经网络拓扑结构，将解空间映射到编码空间。编码长度为

s=nl+ml+l+m

(8)

2) 定义迭代次数iter、种群大小popsize、预分配优胜子群体bestsize和临时子群体tempsize大小。子群体SG大小为：

(9)

3) 选取各个个体和种群的得分函数val。

(10)

SE=mse(T-A2)

(11)

式中：A2为每次迭代后输出层的输出值；T为期望输出；SE为均方差。

4) 不断进行迭代，输出最优个体，并以此作为BP神经网络的权值和阈值，训练网络。

该算法的具体流程如图4所示。

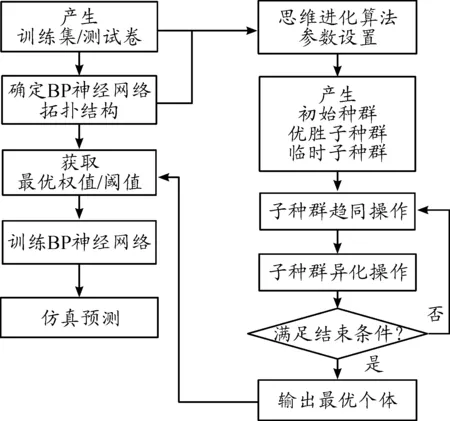
图4 算法流程

当满足迭代停止条件时，思维进化算法结束优化过程。此时，根据编码规则，对寻找到的最优个体进行解析，从而得到对应的BP神经网络的权值和阈值。将优化得到的权值和阈值作为BP神经网络的初始权值和阈值，并利用训练集样本对BP神经网络进行训练、学习。与传统BP神经网络相同，训练完成后，可输入测试集样本进行仿真预测，并可进行结果分析和讨论。

3 非线性函数

为了验证采用BP神经网络和MEA-BP神经网络进行预测时的随机性，采用式(12)所示的非线性函数进行拟合[14]。该函数的图形如图5所示。

(12)

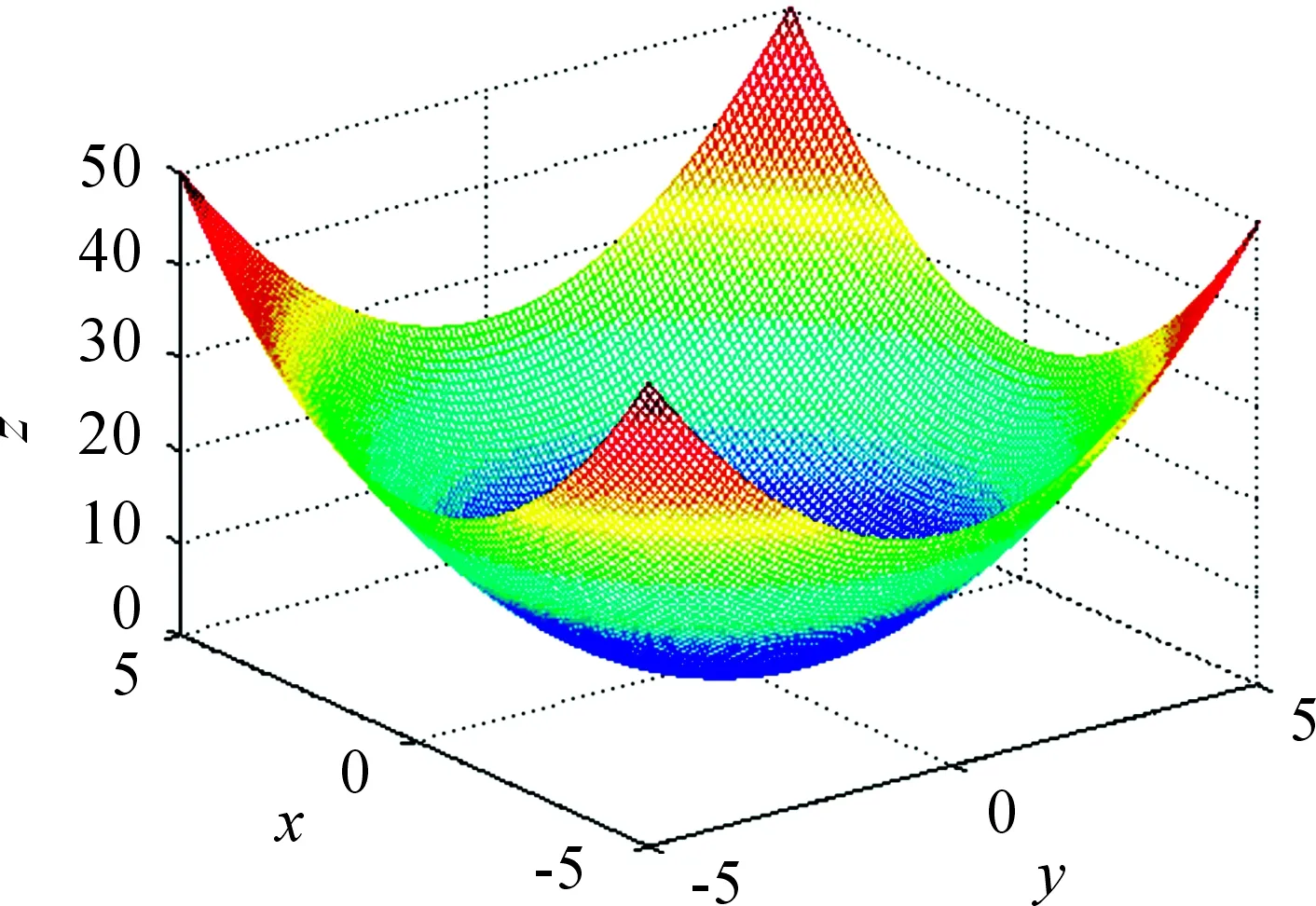
图5 非线性函数图形

此处的BP神经网络训练用非线性函数的输入和输出数据训练神经网络，使训练后的网络能预测非线性函数输出。从式(12)得到2 000组输入输出数据，由中挑选1 900组作为训练集，剩下的100组数据作为测试集。BP神经网络算法流程如图6所示。

图6 BP神经网络算法流程

分别用训练好的BP神经网络和MEA-BP神经网络预测函数输出，预测误差百分比如图7所示。

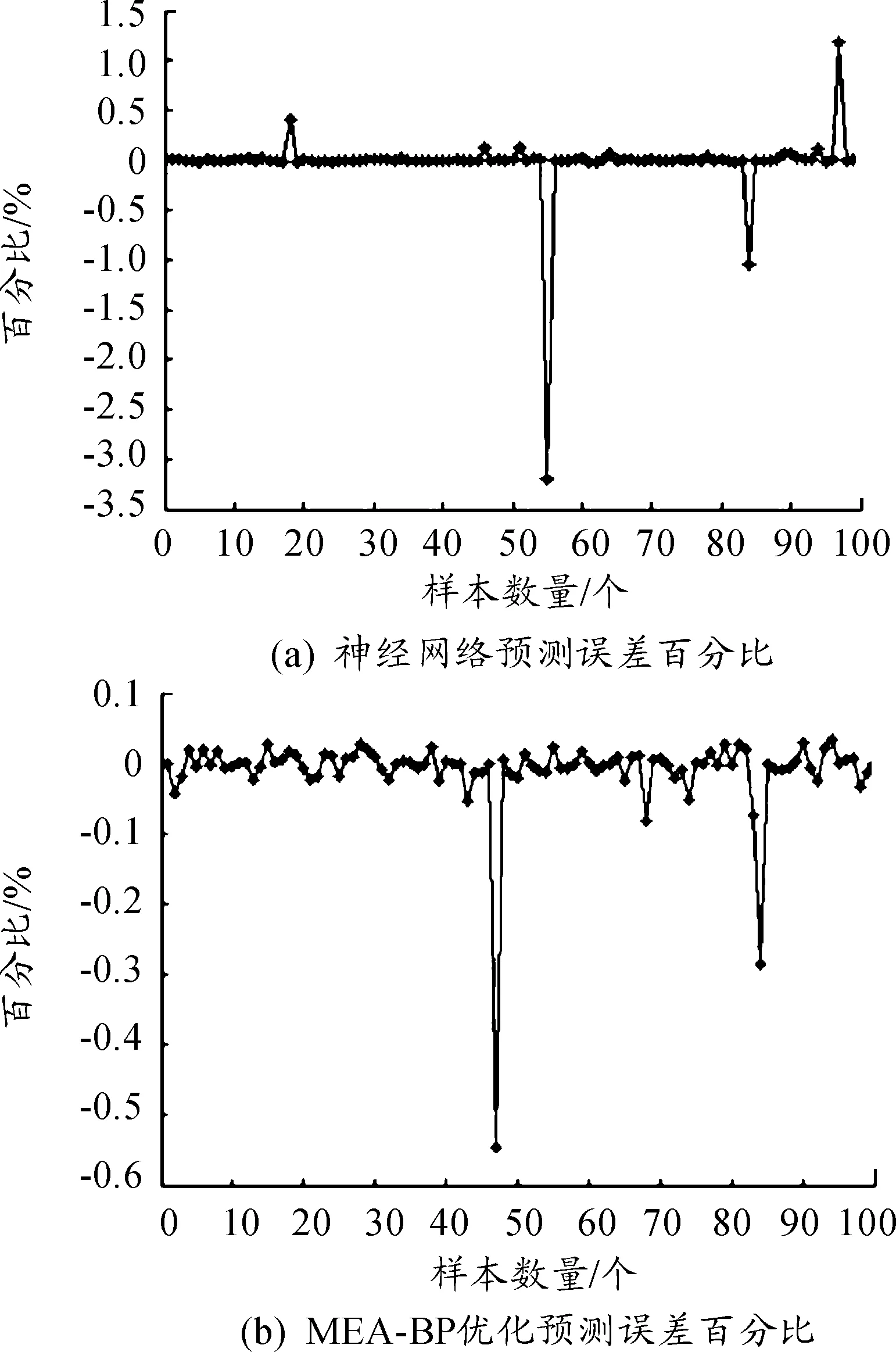
图7 BP神经网络和MEA-BP神经网络预测误差百分比

由图7可知，对于式(12)给出的非线性函数，BP神经网络和MEA-BP神经网络预测结果的误差百分比都维持在0%上下，精度均较高，符合压气机特性曲线预测的使用要求。但是，二者相比而言，采用BP神经网络的预测误差百分比最大能够达到-3%附近，而采用MEA-BP神经网络的预测误差百分比最大只在-0.5%附近，可见采用MEA优化后的BP神经网络具有更好的精度，更加适合实际应用。下文将分别利用这2种方法对压气机特性曲线进行预测和分析。

4 实例分析

本文利用Matlab中的神经网络工具箱建立BP神经网络，采用MEA对BP神经网络进行优化，对压气机特性曲线进行拟合和预测。图8是某型轴流式压气机特性曲线，其中横坐标表示折合流量，纵坐标表示压比。

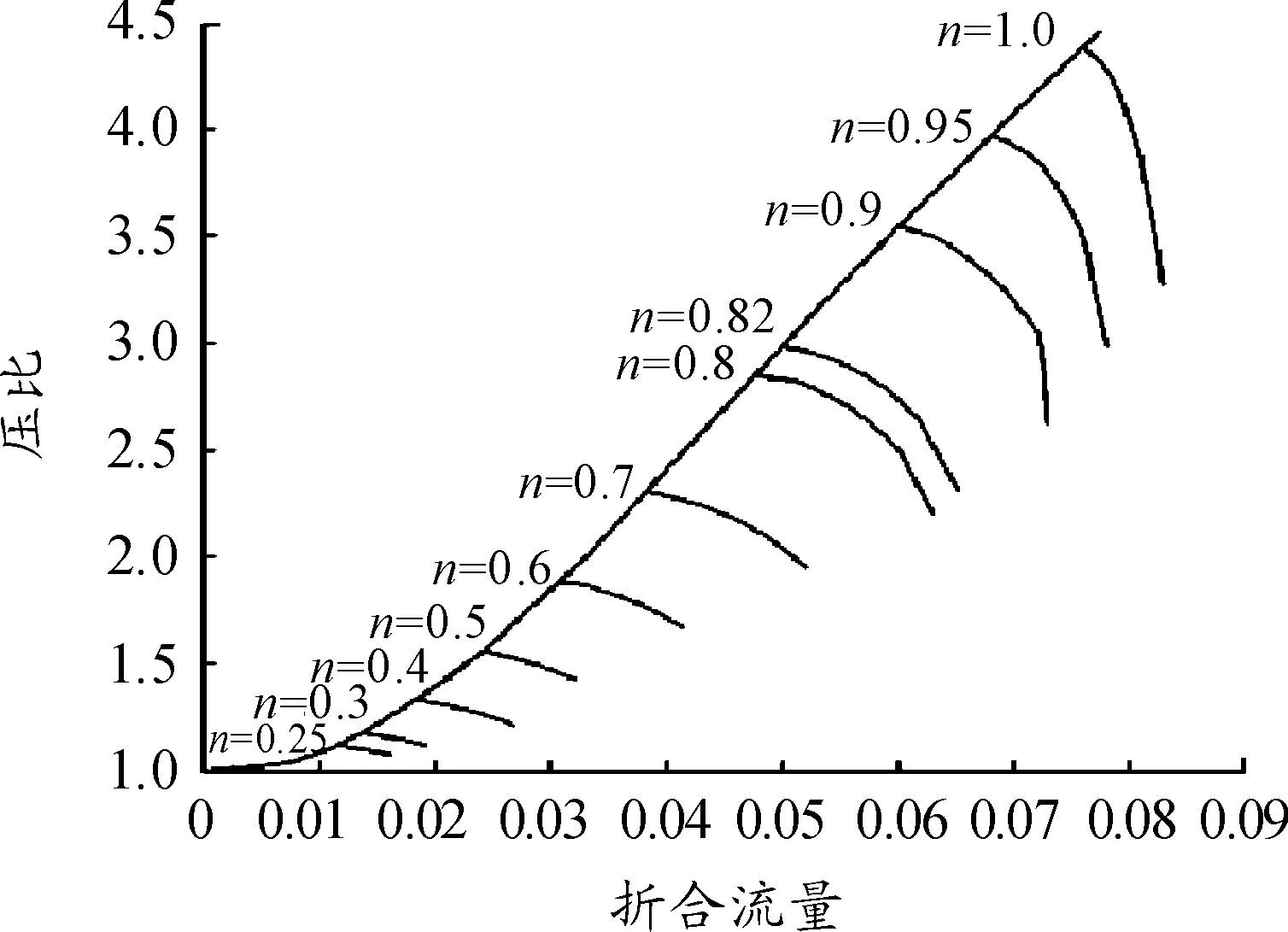
图8 某型轴流式压气机特性曲线

由图8可知，图中共有11条等转速线，分别取转速n=0.9、0.8、0.7、0.6、0.5、0.4、0.3上的样本数据作为神经网络的训练集，每条等转速线上取6个点，而将转速n=0.95、0.82、0.25上的样本数据作为检验数据。其中，n=0.95作为高转速样本外插值，n=0.82为样本内插值，n=0.25作为低转速样本外插值。

经过数据归一化处理，分别进行BP神经网络和MEA-BP神经网络的预测。

4.1 BP神经网络

在没有先进算法优化的情况下，运行独立的BP神经网络进行计算，BP神经网络预测结果如图9所示。

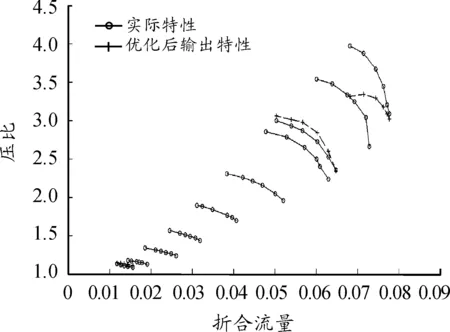
图9 BP神经网络预测结果

图9中，“○”线为训练样本数据的拟合结果，“+”线分别为转速n=0.95、0.82、0.25时BP神经网络的预测结果。

由图9分析可知，对于低转速样本外插值n=0.25和样本内插值n=0.82，独立的BP神经网络预测结果具有较低的相对误差，但是对于高转速样本外插值n=0.95时的误差较大。由此可知，BP神经网络的泛化能力主要针对输入和输出数据都在最大值范围内，即低转速样本外插值和样本内插值，如果是高转速样本外插值，则会有比较高的输出误差。

4.2 MEA-BP神经网络

为了获得更高的预测精度和更好的泛化能力，采用MEA优化算法对BP神经网络的权值和阈值进行优化。相比其他种群类优化算法，MEA具有特有的趋同过程，使优化结果更加准确。针对本案例，MEA优化的BP神经网络初始优胜子种群和临时子种群的趋同过程如图10所示。

由图10可知，经过若干次趋同操作，各子种群均已成熟，即得分不再增加。同时，优胜子种群和临时子种群成熟后，临时子种群中的子种群5的得分比优胜子种群中的一部分子种群得分高，而优胜子种群中的子种群5的得分比临时子种群中的一部分子种群得分低。对于这种情况需要执行一次“异化”操作，同时要补充一个新的子种群到临时子种群中。经过“趋同”和“异化”过程，完成MEA对权值和阈值的优化。

MEA优化的BP神经网络经过训练后，预测结果如图11所示。

图10 MEA-BP趋同过程

图11 MEA-BP神经网络预测结果

图11中，“○”线为训练样本数据的拟合结果，“+”线分别为转速n=0.95、0.82、0.25时BP神经网络的预测结果。

通过对图11分析可知，采用MEA优化后的BP神经网络预测结果误差大多维持在1%以下，具有较好的精度；同时，针对不同的样本外插值和样本内插值都有比较不错的结果，具有较好的泛化能力。

4.3 误差分析

为了分析BP神经网络和MEA-BP神经网络预测结果的准确性和泛化能力，将具体的实际特性图数据和2种方法的预测数据结果统计如表1所示，并将BP神经网络和MEA-BP神经网络预测结果的相对误差百分比进行对比分析。

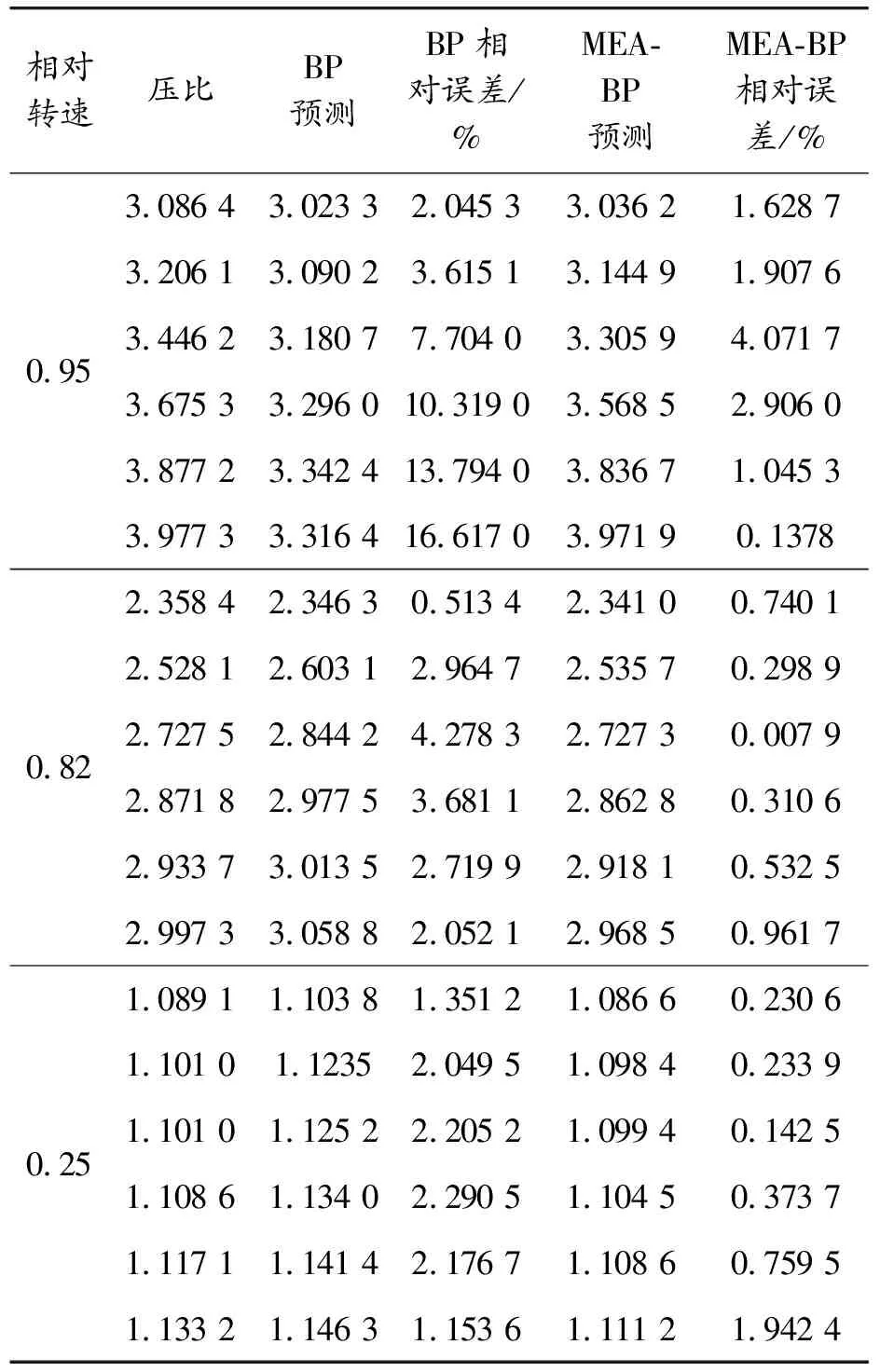
表1 BP神经网络和MEA-BP神经网络预测与实际数据对比

由表1分析可知，采用BP神经网络进行预测时，所得相对误差大多大于2%，其中对于样本内插值和低转速样本外插值的相对误差在2%左右，对于高转速样本外插值的相对误差均大于2%，甚至达到了16%。可见，BP神经网络的泛化能力主要针对输入和输出数据都在最大值范围内，即低转速样本外插值和样本内插值。如果是高转速样本外插值，则会有比较高的输出误差，不适用于燃气轮机的实际工况。

采用MEA-BP神经网络进行预测时，所得相对误差小于1%。对于高转速样本外插值，虽然其误差在1.5%上下，略高于样本内插值和低转速样本外插值的结果，但是相比BP神经网络而言，采用MEA优化过的BP神经网络的相对误差降低了很多。可见，相比BP神经网络，采用MEA-BP神经网络得出的压气机特性曲线预测具有更好的精度和泛化能力，更适用于燃气轮机建模。

5 结论

1) 首次将思维进化算法(MEA)引入压气机特性曲线预测中，分别通过BP神经网络和MEA-BP神经网络进行压气机特性曲线计算，得到了相应的预测结果。

BP神经网络的泛化能力主要针对输入和输出数据都在最大值范围内，即低转速样本外插值和样本内插值。如果是高转速样本外插值，则会有比较高的输出误差。MEA-BP神经网络相比以上2种方法具有明显的优势。采用MEA优化过的神经网络，预测结果误差大多维持在1%以下，具有很好的精度；并且针对不同的样本外插值和样本内插值，都有比较不错的结果。

经过对预测结果的对比分析，发现利用MEA算法优化过的BP神经网络预测效果较好，并且具有很强的泛化能力。

2) 非设计工况下的压气机特性曲线可以通过神经网络计算获得，并且思维进化算法(MEA)能适用于燃气轮机压气机特性曲线的预测。在其优化的情况下，BP神经网络也具有更高的实用价值，适合于压气机的实际运行分析，有利于燃气轮机整体模型的建立与仿真，有助于燃气轮机机组的运行优化。