基于CFD的罗茨真空泵的瞬态流场计算与性能预测

黄 思，康文明，陈首挺，莫宇石

(1.华南理工大学 机械与汽车工程学院, 广州 510640；2.广东省肯富来泵业股份有限公司, 广东 佛山 528000)

罗茨真空泵是一种旋转容积式真空泵，能在较宽的压力范围内工作，且泵腔内无油，目前已广泛应用于半导体、电子、石油、化工等行业的真空系统[1-2]。

罗茨真空泵运行过程中涉及热变形、流量脉动和排气口回流等复杂过程，难以通过理论分析进行研究。随着CFD技术的广泛应用，采用数值计算方法对罗茨泵内部实际流动进行模拟并分析其流动状况成为一种有效手段。国内外学者针对罗茨泵型线、泄漏、内部流场以及进排气流量脉动展开了深入的研究[3-17]。Hsieh等[3]利用实验结合数值分析的方法研究了采用直齿和斜齿转子的罗茨泵的内部流动情况，揭示了两者的内部流动规律。Burmistrov 等[4]建立了分子流态下罗茨泵的泄漏通道流导系数的模型，充分考虑了转子的返流对泄漏的影响。戴映红等[13]从啮合理论出发，研究了各种型线转子的容积利用系数，并对罗茨真空泵内部流动情况进行了瞬态模拟。魏列江等[14]通过对罗茨泵进行数值计算，发现径向间隙是导致泄漏的重要因素。刘正先等[15]运用动网格对罗茨泵内部排气脉动、涡流等进行了相关研究，并修正了泄漏经验公式。目前，关于罗茨泵的研究主要还是基于特定工况展开的，而对于不同工况下罗茨泵性能的系统全面的研究则尚不多见。本文以ZJQ-600型罗茨真空泵为研究对象，对不同压差、转速、转子间隙、有无逆流冷却、进气温度等条件下罗茨泵进行全面系统的研究，探究各参数对罗茨泵性能的影响，并将数值计算结果和抽速实测结果进行对比，以验证计算模型的有效性。

1 气体流动的控制方程

罗茨真空泵内气体视为可压缩理想气体，其工作过程属于流动与传热的耦合问题，满足下列的连续性方程、动量方程、能量方程及气体状态方程：

(1)

(2)

(3)

(4)

其中：ui是速度矢量在i方向的分量；ρ为气体密度；μ为动力黏度；cp为气体比热；λ为气体分子导热系数；R为气体常数；Si为动量守恒方程的广义源项；ST为黏性耗散相。

2 罗茨真空泵流场的计算

2.1 流体域建模与网格划分

所研究的ZJQ-600型罗茨真空泵示意图如图1所示，包括吸气腔、携带腔、逆流冷却段和排气腔，其中入口直径D1=200 mm，出口直径D2=150 mm，逆流冷却口直径D3=75 mm，中心距L=208.2 mm，转子厚度B=420 mm，设计转速n=1 460 r/min。逆流冷却就是在罗茨真空泵基元容积与排气口连通之前，从排气口引回一部分高温高压气体，经冷却后进入图1所示的逆流冷却口，使基元容积内部压力预先接近排气压力。

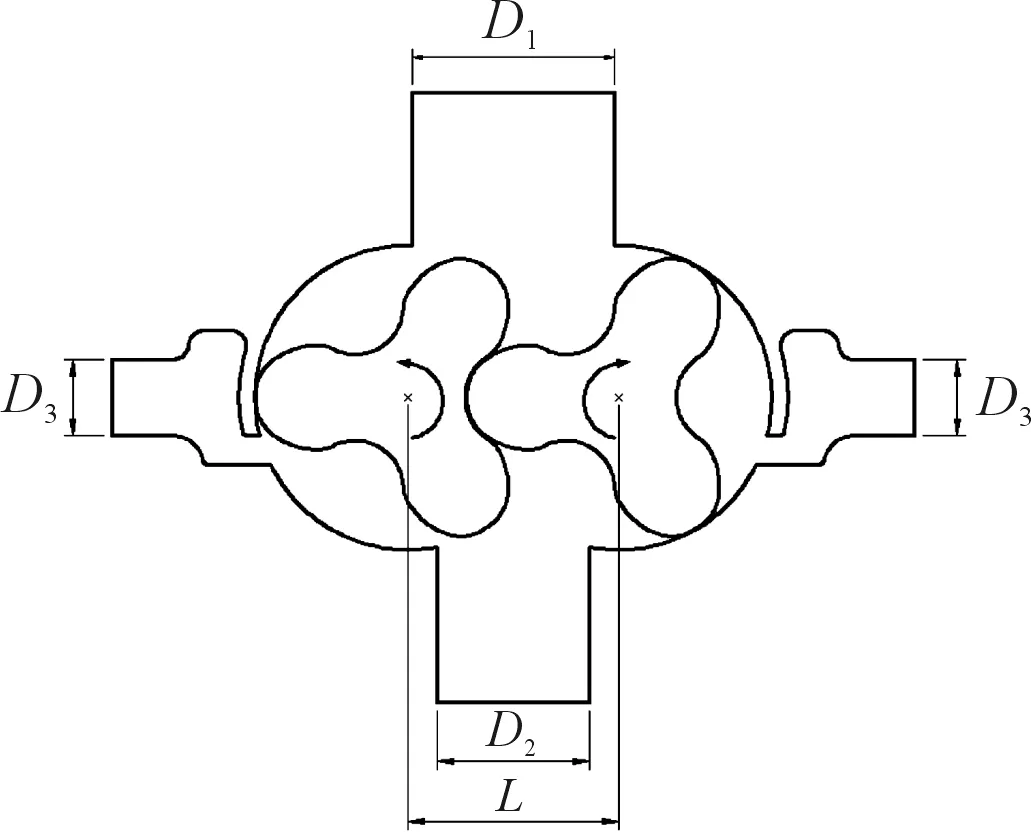
图1 罗茨泵示意图

由于罗茨真空泵进排气容积呈周期性变化，计算域与网格随时间的变形和位移十分显著，因此在现有的CFD技术中只有动网格才能实现这种状况下的瞬态模拟。本文采用局部网格再生成和弹性光滑模型来实现动网格以适应实际流场的需要。对建立好的流体域模型进行网格划分，结果如图2所示，网格总数为 473 725。

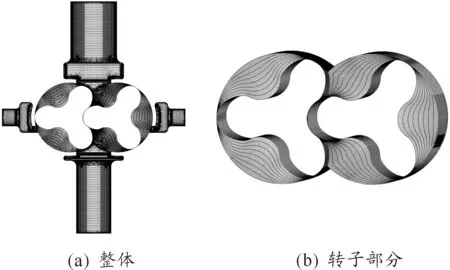
图2 罗茨泵计算域网格划分

2.2 操作条件设置

运用CFD动网格技术进行罗茨泵的瞬态流场计算。选择RNGk-ε模型，该模型能够更好地处理高应变率及流线弯曲程度较大的流动。压力项用PRESTO格式离散。其余项用二阶迎风格式离散。压力速度耦合方程采用PISO算法求解。设置材料为理想空气，边界条件设置为压力入口和压力出口。根据罗茨泵的最大转速，计算设置时间步长为10-5s。

2.3 计算结果验证

设置出口压力pd为大气压，分别计算入口压力ps=101 325、60 000、45 000、30 000、25 000和20 000 Pa(绝对压力，下同)时罗茨泵的抽速qs。图3是不同ps下计算抽速qs在一个周期内的平均值与实测抽速的对比。由图3可以看出：在ps比较大(大于30 000 Pa)时，计算结果与实际抽速比较接近；ps较低时(25 000 Pa)，计算结果与实际抽速偏差较大，偏差较大的原因是当进出口压比pd/ps较大时，泵内温度较高造成了转子和泵壳等热膨胀变形而产生了较多的泄漏。

2.4 内部流场分析

图4和图5分别是基元容积未与排气口连通时，有、无逆流冷却装置罗茨泵的流速矢量和压力分布。结合图4、图5可以看出：高压冷气持续流入逆流冷却罗茨泵基元容积内，形成较大的旋涡，致使基元容积内压力不断增大，接近甚至超过排气口压力。图5(b)基元容积内的2个低压区对应于图4(b)中的旋涡中心。无冷却罗茨泵流动过程则相对较平稳，图5(a)基元容积内压力接近吸气腔，但由于存在泄漏，基元容积内压力在转动过程中略有增大。

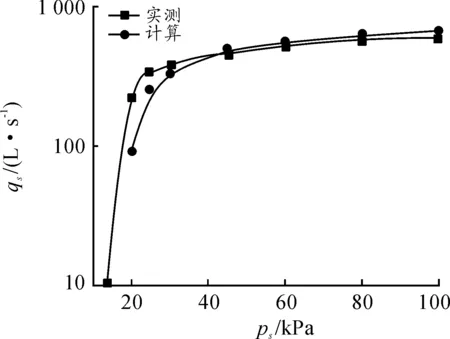
图3 抽气速率的实测值和模拟计算值的对比

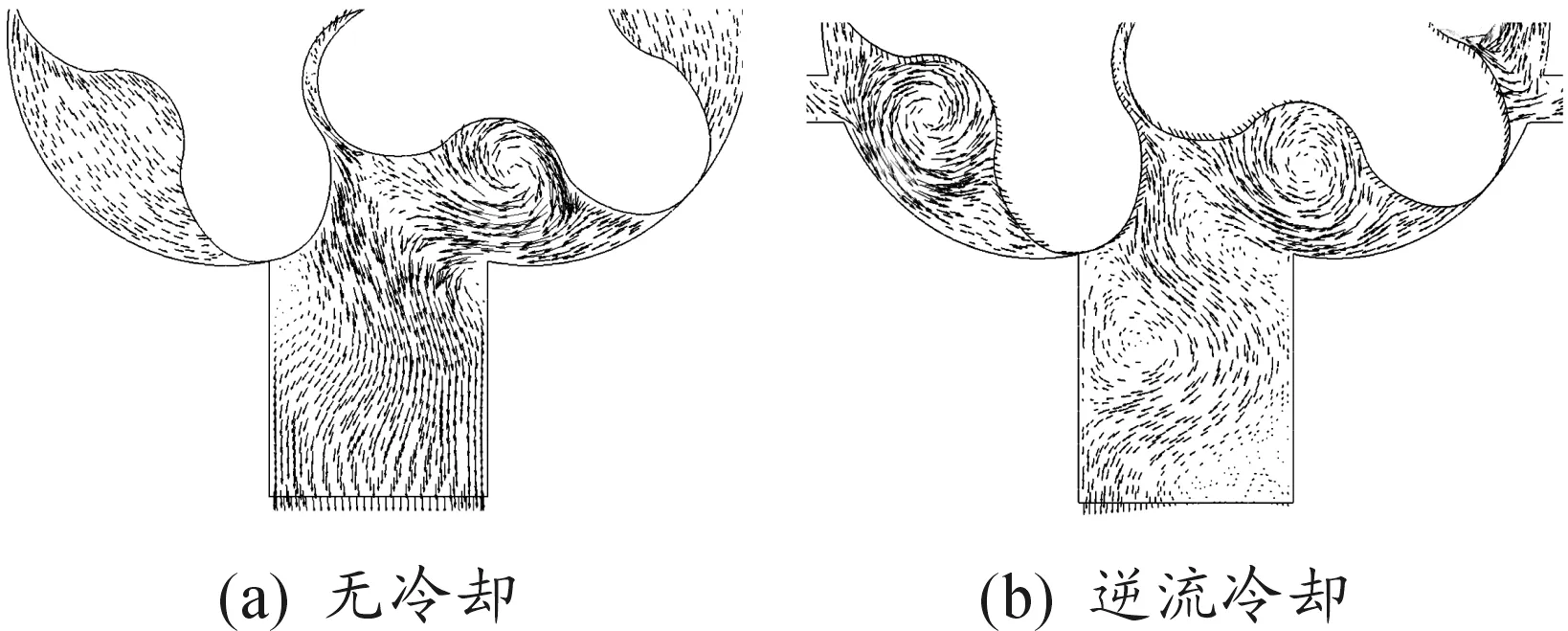
图4 基元容积未与排气口连通时流速矢量

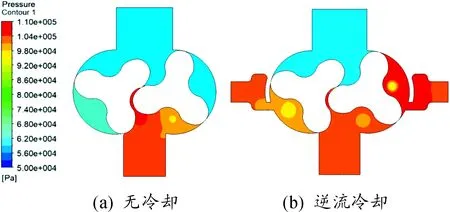
图5 基元容积未与排气口连通时压力分布

图6和图7分别是基元容积与排气口充分连通后有、无逆流冷却装置罗茨泵的流速矢量和压力分布。结合图6和图7可以看出：由于逆流冷却的预进气使封闭的基元容积在与排气口连通之前，内部压力已达到或接近排气压力，所以此时并无明显的回流现象，大幅度降低了排气时的气体回流及其带来的气流噪声；无逆流冷却罗茨泵在排气初始时排气腔与基元容积间存在极大的压差，当基元容积与排气腔连通后，排气侧的高压气体迅速均压回流，图6(a)中回流气体与基元容积中的排出气体相遇，在连通处形成旋涡。

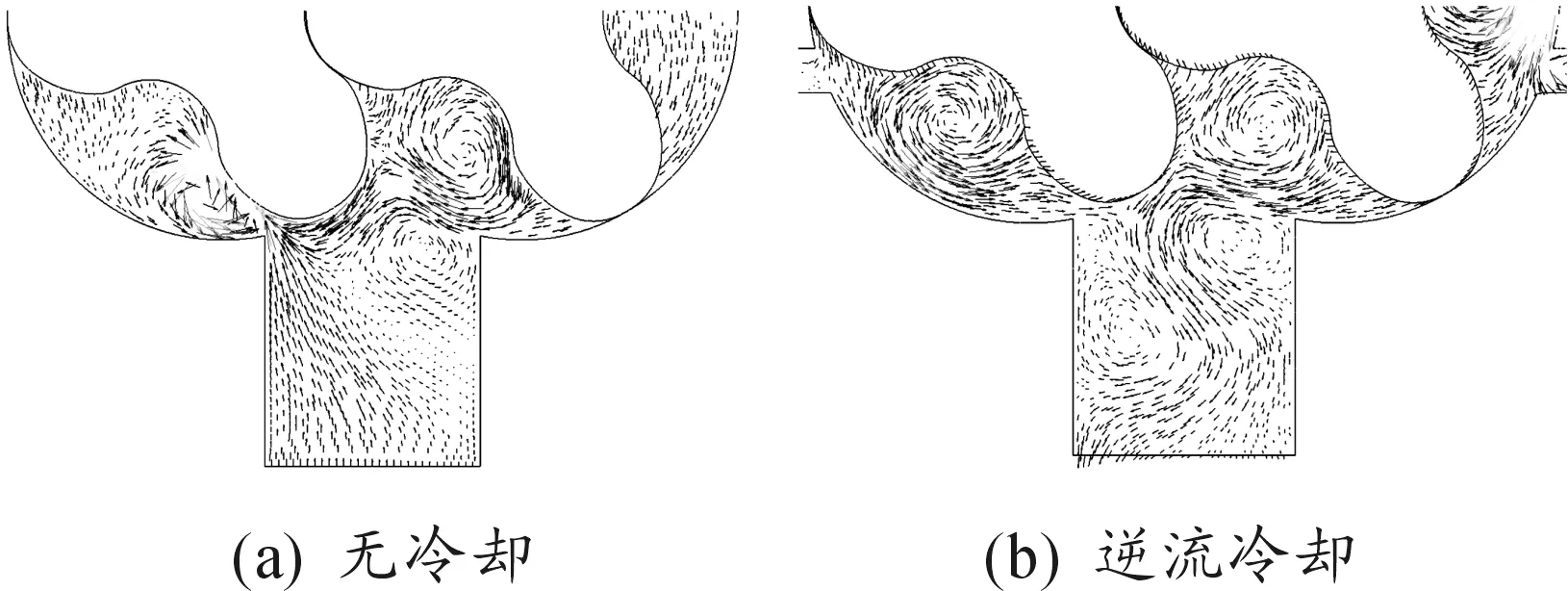
图6 基元容积与排气口连通后流速矢量

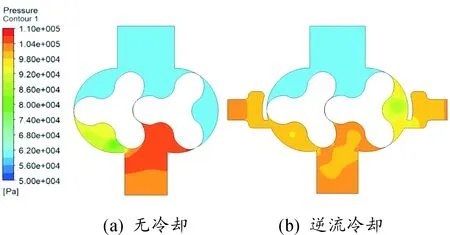
图7 基元容积与排气口连通后压力分布

3 各种参数对抽速的影响

3.1 入口压力

图8是出口压力为101 325 Pa时分别计算ps=101 325、60 000和45 000 Pa得到的罗茨泵稳定运行后qs随转动角度θ的变化，qs的平均值分别为675、550.7和496 L/s。由图8可知：在一个转子旋转周期内，qs随时间出现6次谐波变化，频率正好是罗茨泵转子叶片数的2倍，这是2个转子交互作用所产生的结果。在入口压力较高时，抽速平稳，脉动幅度小，随着入口压力的降低，气体脉动强度增大。不同入口压力下波峰的位置不同，即抽速达到最大值的转子角度并不一致。

3.2 转速

图9是入口压力6 000 Pa、出口压力14 100 Pa和入口压力60 000 Pa、出口压力101 325 Pa两种工况下的qs随转子转速n(980、1 460、1 750 r/min)的变化曲线。由图9可知：抽速和转速大致呈线性关系，满足流量相似定律，即几何相似的泵在相似工况下运行时，其流量比与转速比的一次方成正比。

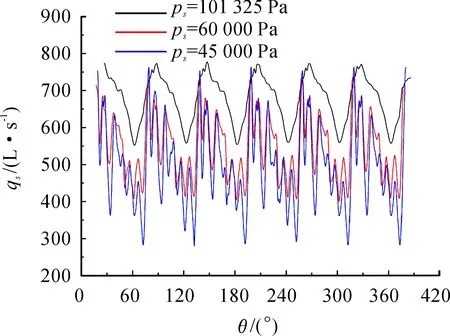
图8 不同入口压力下抽速随转子转角的变化

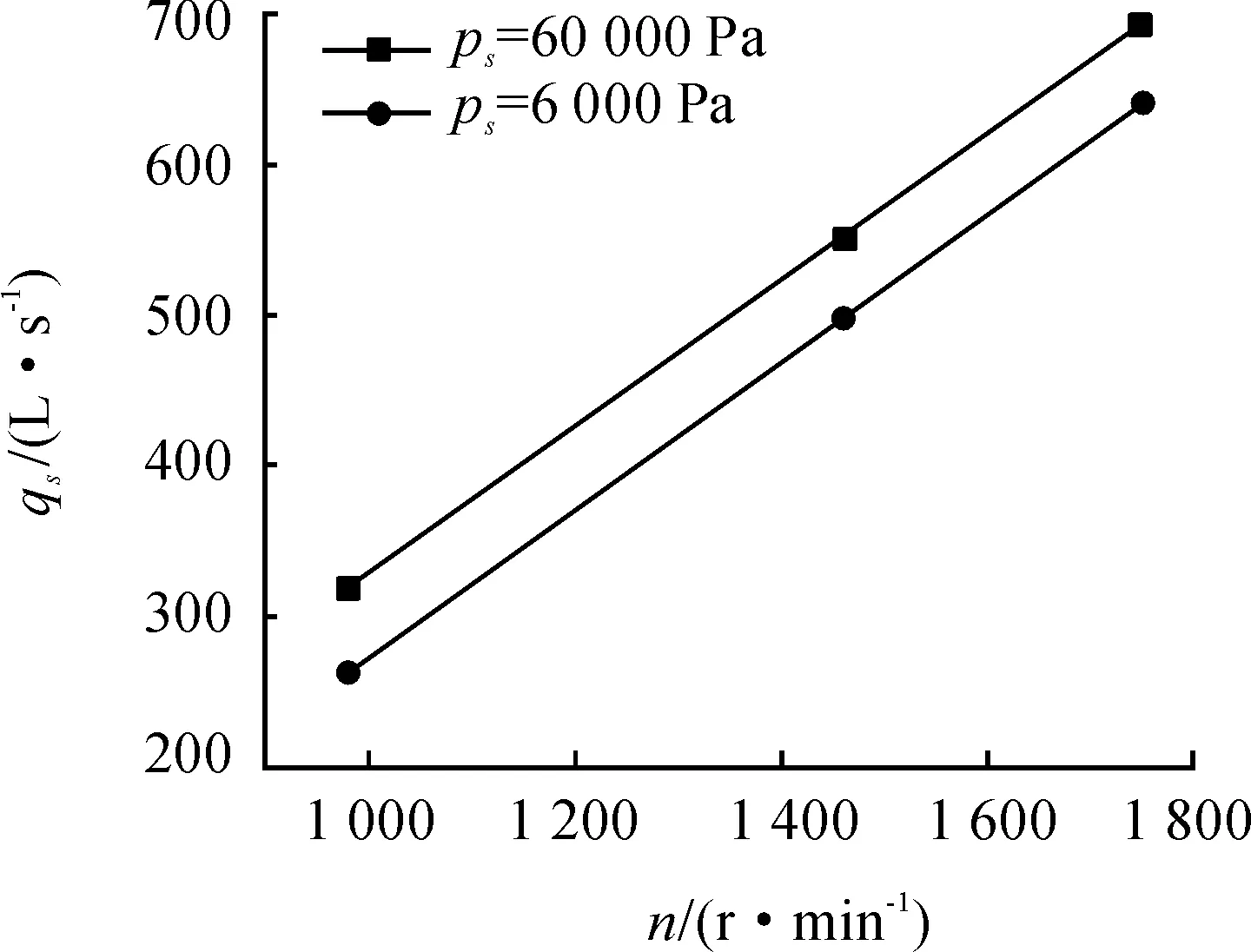
图9 转子转速对抽速的影响

3.3 转子间隙

图10是入口压力为 60 000 Pa，出口压力101 325 Pa时qs随转子间隙δ(0.15、0.2、0.6、0.8 mm)的变化曲线。由图10可知：抽速随着转子间隙的增大而逐渐减小，但减小的趋势不断变缓。在间隙较小时，泄漏速度较大，抽速对转子间隙变化比较敏感。

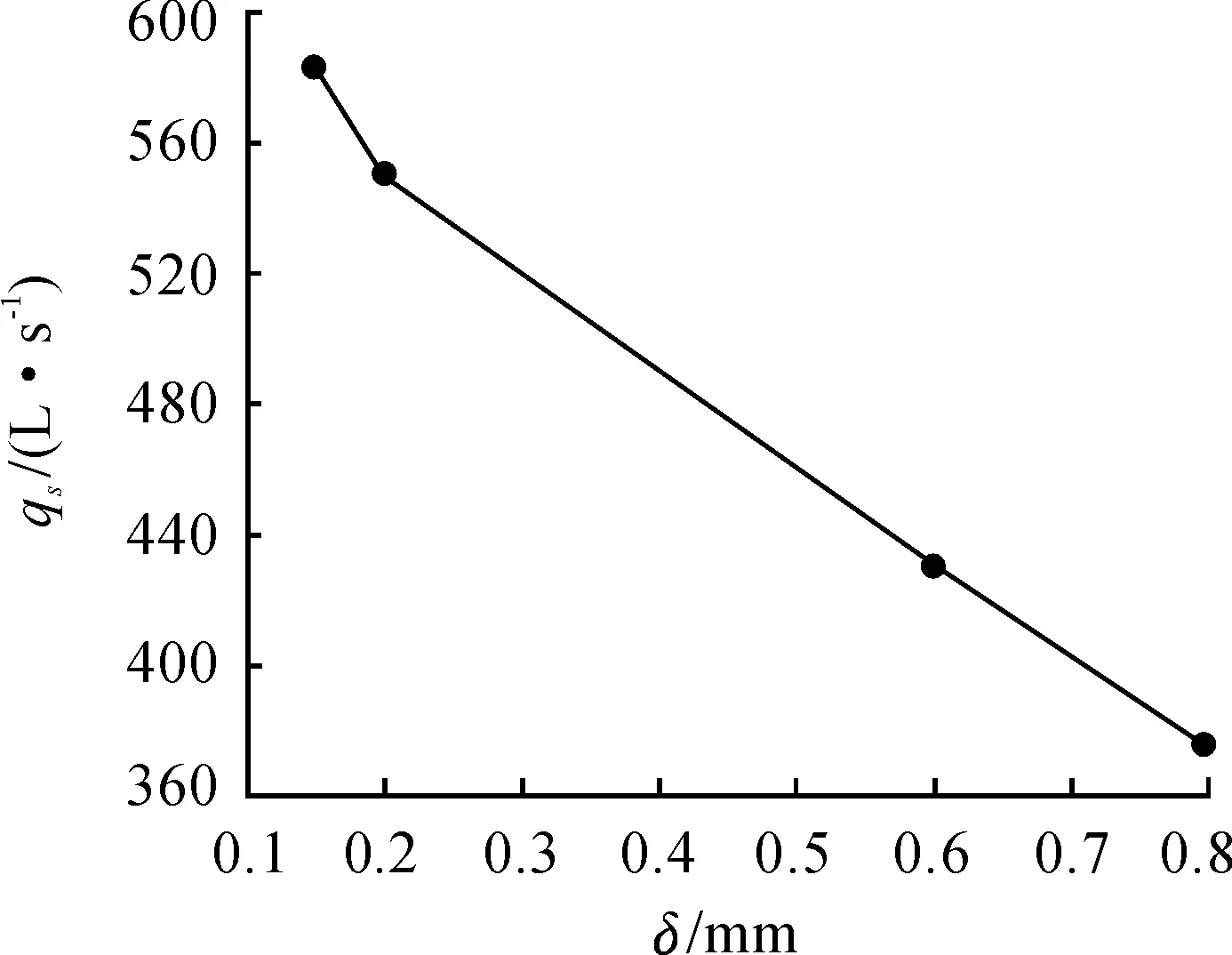
图10 转子间隙对抽速的影响

3.4 逆流冷却

图11是入口压力为60 000 Pa时，有无逆流冷却2种工况下罗茨泵稳定运行后qs随转子转角θ的变化曲线。

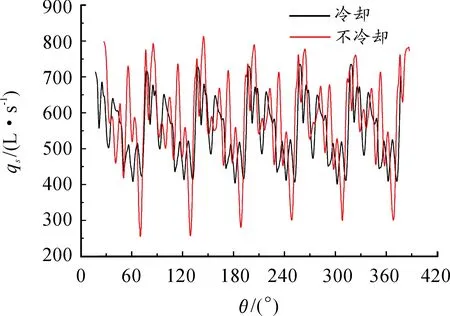
图11 逆流冷却对抽速的影响

由图11可知：无逆流冷却的抽速脉动幅度大于有逆流冷却的罗茨真空泵，且平均抽速577.4 L/s，略大于有逆流的550.7 L/s。这是因为此时压比不大，排气温度较低，当不考虑转子及泵壳的热膨胀变形给流体域带来的影响时，增加逆流冷却装置将会使压缩过程提前，压缩周期延长，基元容积中气体压力大致接近排气压力，会有更多的气体向进气腔泄漏；同时增加逆流冷却装置会使基元容积以及预冷进气通道中产生较大的旋涡，严重阻碍了气体向排气侧流动。

3.5 进气温度

图12是入口压力为60 000 Pa时，进气温度ts分别为20 ℃和60 ℃两种工况下罗茨泵稳定运行后qs随转子转角θ的变化曲线。计算得到20 ℃和60 ℃时的平均抽速分别为550.7 L/s和547 L/s，出口排气温度分别为50 ℃和53 ℃。从图12可以看出：两者的脉动幅度和脉动频率大致是一样的，在同一转子转角时有最大抽速。在压比较低时，进气温度对抽速的影响较小，抽速随进气温度升高略有下降。

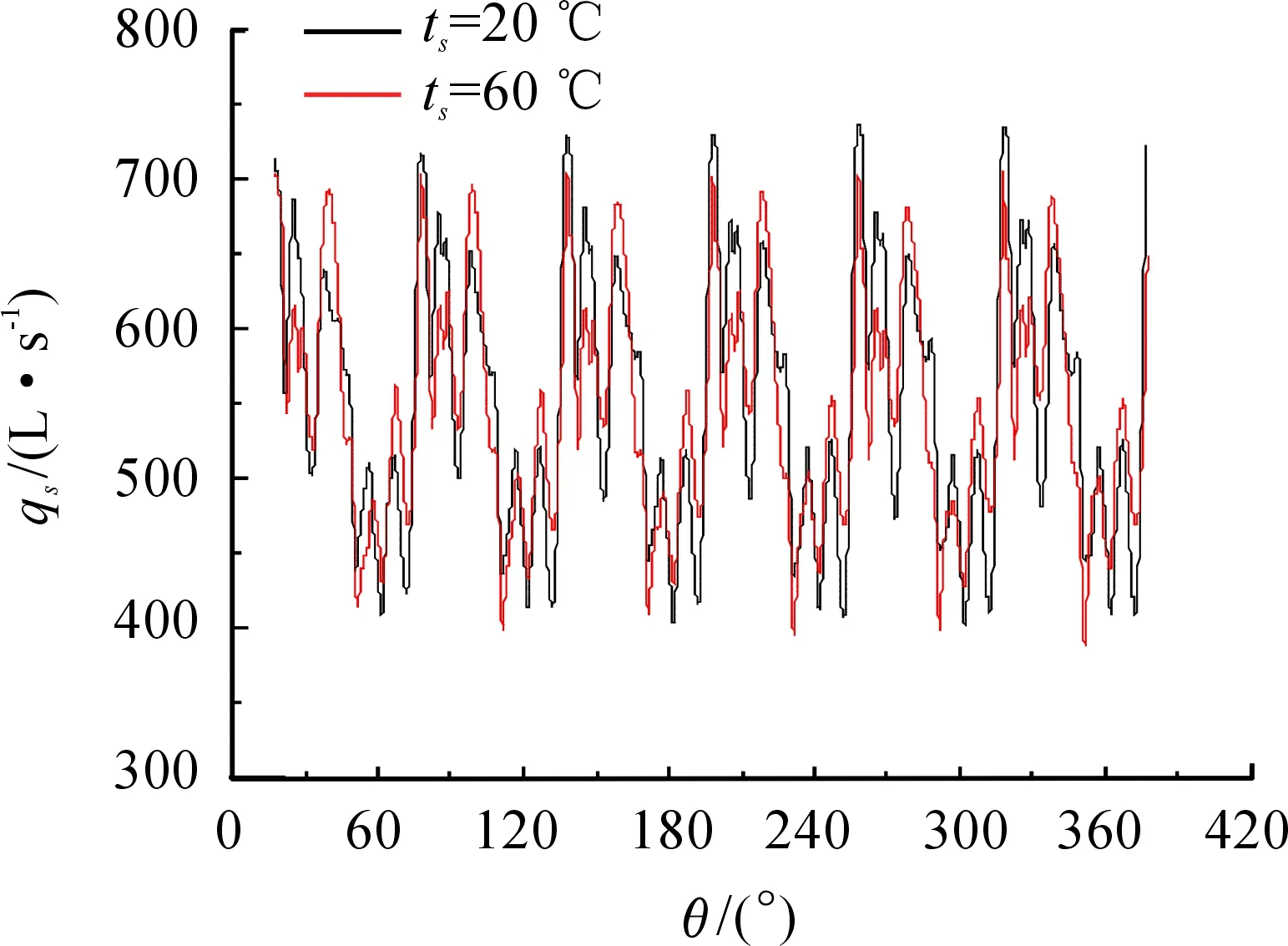
图12 进气温度对抽速的影响

4 结论

本文通过对罗茨真空泵流场数值计算并与实测抽速进行了对比，得到以下结论：

1) 逆流冷却排气口连通之前基元容积内部压力已达到排气压力，所以排气口并无明显的回流现象；无逆流冷却罗茨泵在排气初始时排气腔与基元容积间存在极大的压差，当基元容积与排气腔连通后，排气侧的高压气体迅速均压回流，在连通处形成旋涡。

2) 系统研究了各参数对罗茨泵性能的影响，得到罗茨真空泵的性能变化规律。出口压力一定时，随着入口压力降低，抽速减小，流量脉动剧烈。抽速和转速线性相关，近似满足流量相似定律，抽速比与转速比的一次方成正比。抽速随着转子间隙的增大而逐渐减小，但减小的趋势不断变缓。

3) 当压比较小时，增加逆流冷却会使基元容积以及预冷进气通道中产生较大的旋涡，阻碍气体向排气侧流动。因此，增加逆流冷却并不能增大抽速，抽速随进气温度升高略有下降。