等离子体控制下后台阶流动的数值模拟

王靖宇，周申申，胡兴军

(吉林大学 a.汽车仿真与控制国家重点实验室; b.汽车工程学院, 长春 130022)

在过去的几年中，主动流动控制概念已经成为流体力学中一个越来越吸引人的话题。等离子体流动控制作为主动流动控制的一种，具有结构简单、能耗低、动态响应快等优点，近些年来广受国内外学者的关注。等离子体是区别于固体、液体、气体的物质存在的第4种状态，包含大量离子和与之成对出现的电子，广泛存在于大气层外的真空中[1]。生活中，高温、高压以及闪电等条件下，也可产生一定量的不稳定等离子体。采用在两高压电极板间添加绝缘介质的方式(dielectric barrier discharge，DBD,介质阻挡放电)，可产生稳定的等离子体[2]，其结构如图1所示。其中，上电极接电源的正极，下电极接电源的负极，中间为绝缘介质层，当电压达到某一确定值，在上电极右侧产生稳定的淡紫色气体，即为等离子体。其流动控制原理为：一方面，上电极极板附近产生辉光放电，将部分空气电离，电离产生的电子和离子在电磁场的驱动下，与空气分子发生碰撞，进行能量与动量的交换，从而带动周围空气产生集体性定向运动；另一方面，在空气电离过程中，产生一定的温度升和压力升，以脉冲的形式对外做功；二者共同作用使上极板附近空气定向运动获得一定的速度。

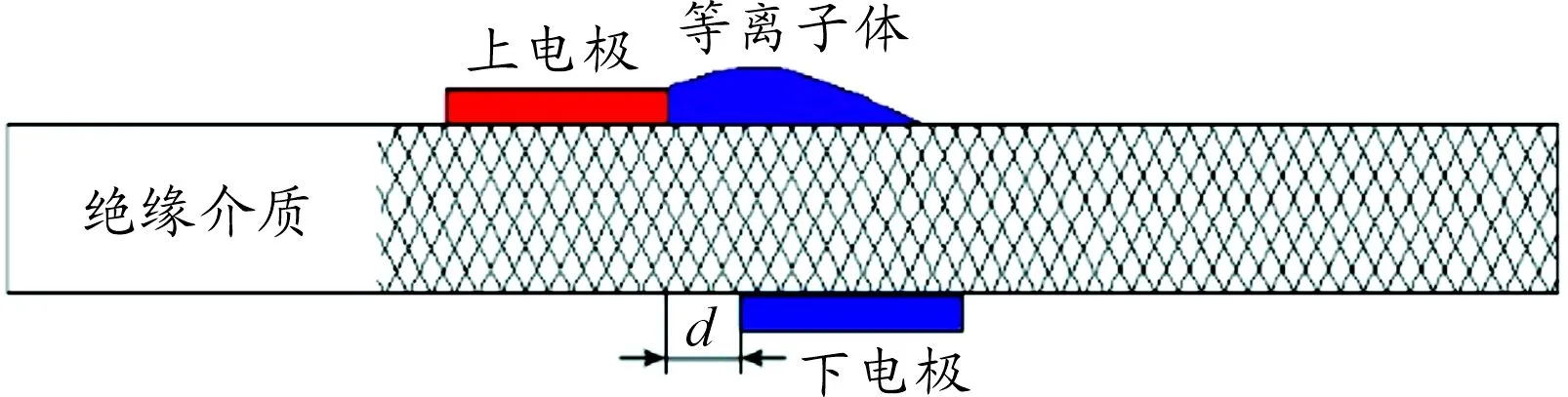
图1 DBD基本结构示意图

后台阶流动(backward-facing step,BFS)是流体力学中的一个典型的流动分离、再附着模型，其几何模型如图2所示，它代表着一类横截面突增的钝状体绕流问题[3]，在其台阶后部会出现流动的分离和再附着现象。流动的分离会产生许多负效应，如阻力增加和噪声产生等，因此控制分离区的大小、减小再附着长度是研究的重点。

郑朝荣等[3]运用后台阶流动模型，在台阶下部进行向台阶方向的抽气，以减小再附着长度，得到抽吸强度越大，对再附着位置前移控制效果越明显的结论。王斌等[4]使用等离子体对后台阶流动进行45°方向射流控制，通过PIV试验观察再附着位置的前移。Boom Y J等[5]运用后台阶流动模型，在台阶上部施加等离子体流动控制，降低分离区的湍动能、减小再附着长度。

图2 后台阶流动模型

本文使用CFD仿真软件Fluent，采用k-ω湍流模型[6]，在台阶后部施加等离子体流动控制来降低湍流区的大小、减小后台阶流动的再附着长度。探究在不同来流风速、不同激励电压强度下对后台阶流动的控制效果和等离子体的最佳控制位置。本文的研究结果对应用等离子体对流场进行主动流动控制，从而实现减阻降噪具有一定的指导意义。

1 等离子体模型的仿真与验证

运用Fluent软件进行相关仿真计算，其原理基于N-S方程，表达形式为：

(1)

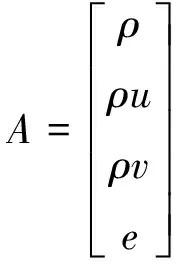
(2)

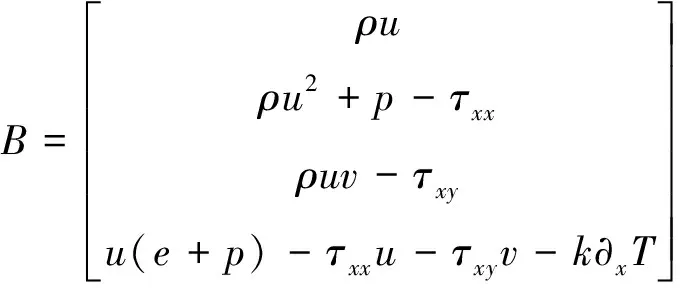
(3)

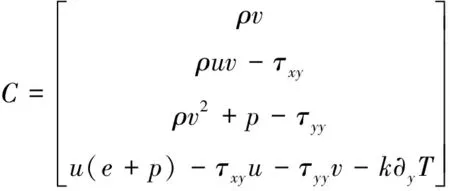
(4)

(5)

式中：ρ为空气密度；e为内能；u、v分别为x、y方向的速度；p为压强，T为温度；τ为剪切力。2002年，W.Shyy等[6]参照Croke和Roth等[7]的试验将介质阻挡放电(DBD)等离子体的流动控制效果进行数值模拟仿真。W.Shyy等综合考虑等离子体激励电压、频率、极板几何形状等因素，将试验工况时等离子体的流动控制效果用如下方程表示：

Ftave=ϑαρeΔtEδ

E=U/D

(6)

式中： ϑ为交流电频率，取3 kHz；α为与粒子间弹性碰撞有效系数，取为1；ρ为电离出的离子密度;e为电子电荷量；Δt为单位周期内有效击穿空气时间，也即瞬时电压大于空气击穿电压时间，取67 μs；E为电场强度；δ为表达等离子体控制区域的常数，取0或1，具体取值取决于当地电压与空气击穿电压的大小，如在三角区范围内δ为1；激励电压U为2.262 7 kV。将式(6)以体积力的形式添加到N-S方程中作为源项，通过编写UDF加载到Fluent软件中。经验证，满足试验精度，随后便广泛被相关学者引用、验证。

本文运用三维长方体空腔进行等离子体的数值模拟仿真，将地面作为等离子体施加位置。由于等离子体的产生及在电磁场作用下的运动核心区大小为3 mm×1.5 mm，因此在产生等离子体处需对网格进行加密，本文在该处最小尺寸取0.1 mm，使该区域内有足够的网格数，以呈现离子与空气分子作用的体积力随远离电极板而衰减的趋势。其几何模型纵向中截面如图3所示。

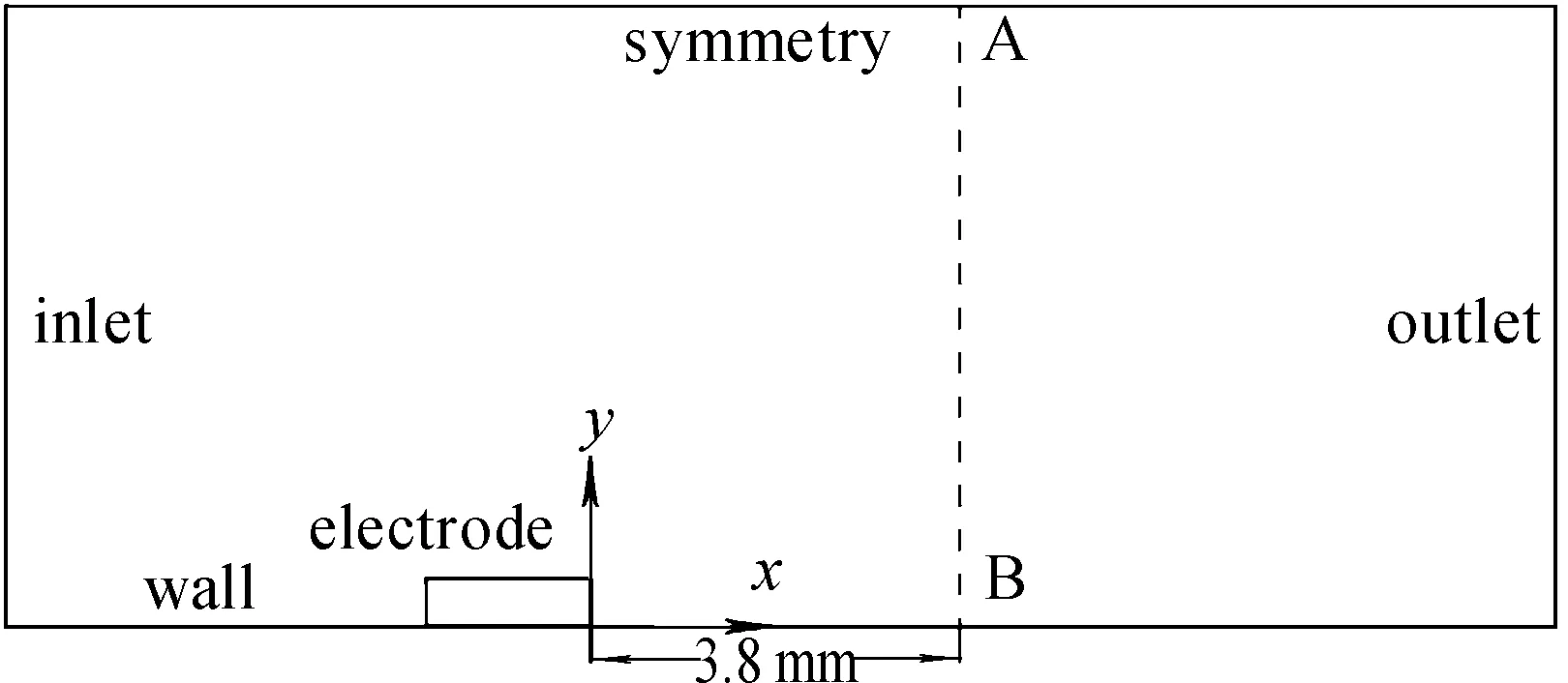
图3 几何模型纵向中截面示意图

边界条件的设置为：入口为速度入口，速度值为0 ；出口为压力出口，压力值为0 ；上壁面为对称壁面；底面为固定壁面。将上述方程编写的UDF以体积力的形式加载到Fluent中，由于等离子体核心作用区域大部分处于边界层内部，故为准确描述等离子体对近壁面流动的控制效果，选取湍流模型为SSTk-ω。经迭代后仿真得到的速度云图如图4所示。

图4 仿真得到的速度云图

由仿真结果可以看出：施加等离子体的流动控制效果为对近壁面附近空气诱导出向右的速度，该诱导气流在后续的发展过程中形成斜向上的逆时针涡流。为检验仿真结果的准确性，在正极板右侧3.8 mm处，作垂直于地面纵向中线的一条线,如图3右侧虚线AB。考察此虚线上沿y轴的速度分布，并将本文仿真结果与W.Shyy仿真结果进行对比，如图5所示。

图5 与W.Shyy仿真结果对比

不同来流风速下最大诱导速度如表1所示。

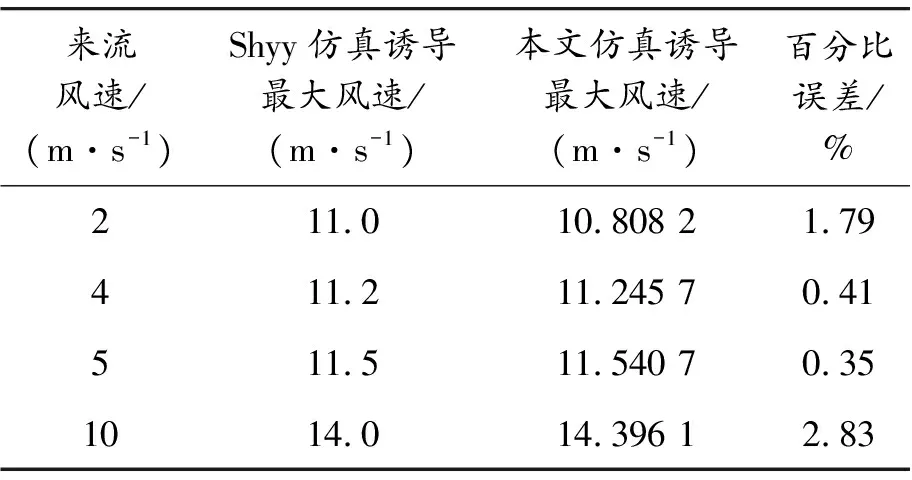
表1 仿真数据对比

由图5和表1可以看出，各种来流风速下诱导最大风速的误差小于3%，由此验证本文对等离子体仿真的准确性。

2 后台阶流动的数值模拟

2.1 几何模型与计算域

本文采用的三维后台阶流动几何模型如图2所示。其中h为台阶高度，取h=25 mm。为使流动充分发展、对分离点和漩涡结构影响尽量小，模型台阶前发展区域为6h，台阶后区域取20h，宽度取4h。

2.2 网格方案

在ICEM-CFD软件中进行相应网格的划分，整体采用非结构网格，进行网格无关性验证后发现，整体最大网格取5 mm即可达到仿真精度要求。之后对产生等离子体的局部区域进行网格加密，加密处网格尺寸取0.1 mm。为探究等离子体最佳控制位置和控制效果，等离子体可能施加的位置处于3h～5h之间，对该区域也进行相同的加密。为准确仿真流动分离点即台阶顶点处的流动状况，对台阶顶点处进行加密，最终网格方案如图6所示。这样生成体网格总数为1 100万。

图6 网格方案

3 计算及结果分析

3.1 来流风速对等离子体控制的影响

边界条件的设置如表2所示。

表2 后台阶流动所选边界条件

在本文所述网格方案的基础上，采用双精度的计算方法在Fluent软件中迭代计算。湍流模型为SSTk-ω，入口为速度入口，速度值为5～20 m/s；出口为压力出口，压力值为0；上壁面为对称壁面；底面为固定壁面。本文采用5 m/s自由来流风速为基准工况，迭代计算得其速度矢量图，如图7所示。

绘制底面中线上的剪切力图，如图8所示。

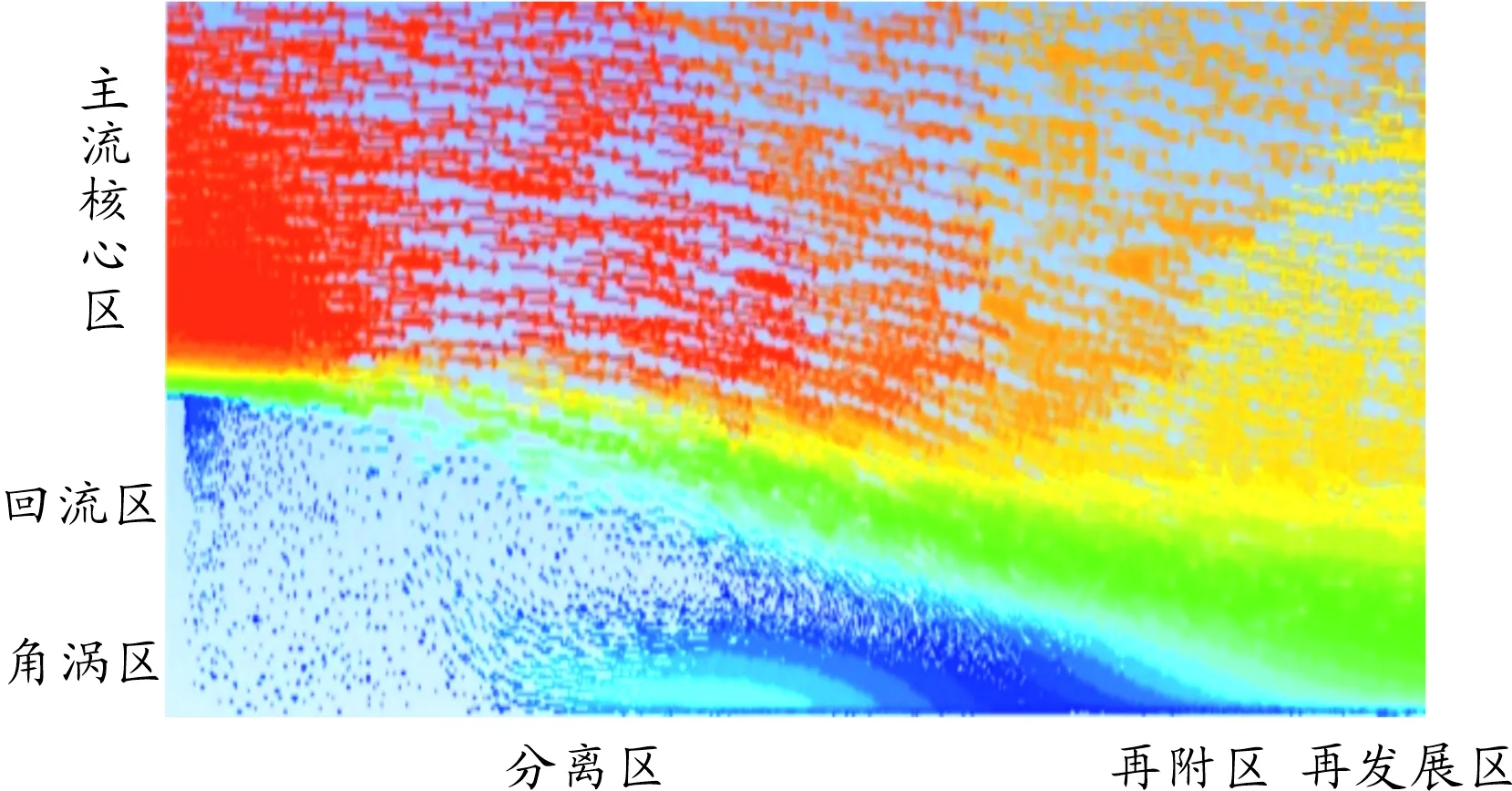
图7 风速5 m/s时后台阶流动速度矢量图

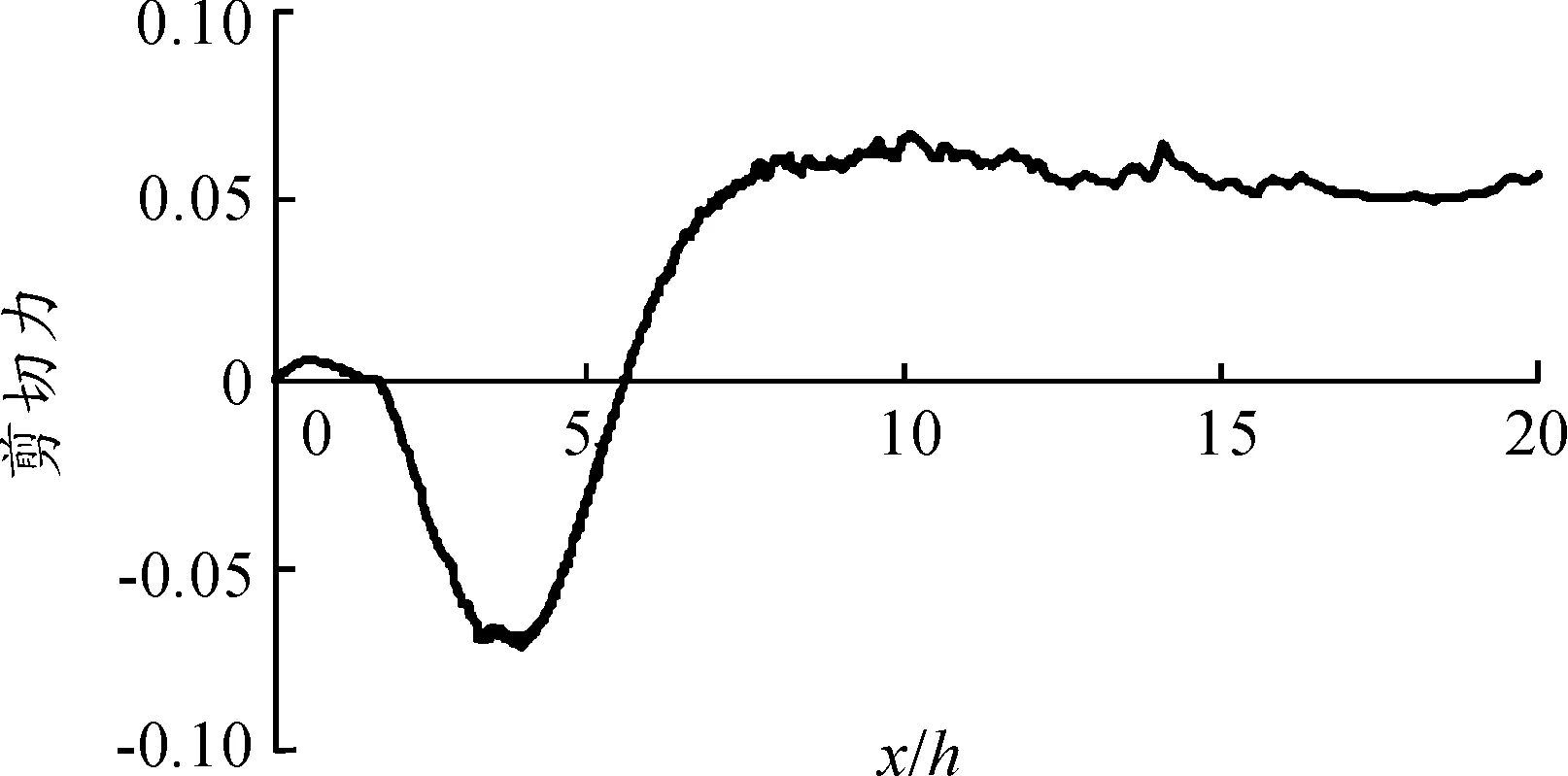
图8 来流风速5 m/s时底面中线的剪切力

由后台阶流动(BFS)的速度矢量图(图7)可以看出，BFS的流场沿竖向分为：角涡区、回流区和主流核心区；沿横向分为：分离区、再附区和再发展区[4]，如图中标示区域。整个后台阶流动分离区主要由一个大的顺时针涡和左下角的逆时针的小涡组成：在图8中剪切力均为负值的区域，对应速度矢量图为顺时针旋涡；在靠近原点时，出现一部分正值，对应速度矢量图中逆时针的小涡，这两部分即对应回流区和角涡区。这说明了BFS的漩涡区由主涡系和一个反向小涡共同组成，这些流场也被Saric等[8]的试验所证明。

由底面壁面剪切力图可以得到后台阶流动的再附着点为x/h=5.547 3，该数值与Uruba等[9]的裂膜探针测量结果x/h=5.625接近，误差较小，为1.837%，验证了本文仿真方法的准确性，为后续施加等离子体的相关仿真奠定了基础。

在此基础上，保证5 m/s的风速恒定，将介质阻挡放电等离子体(DBD)模型施加到台阶后部、再附着点之前，以0.1h为单位，左右调节等离子体施加的位置，观察速度矢量图及剪切力图以找到最佳控制位置。这里以来流风速为5 m/s时，等离子体作用在x=3h、3.1h为例说明等离子体最佳作用位置的确定，如图9所示。

图9 等离子体不同施加位置与基础工况剪应力对比

在3h施加等离子体时，剪切力变为正值出现在2.9h附近，但在4.25h附近处，剪切力又变为负值，说明2.9h处并非再附着位置，而4.25h处才对应该工况下的再附着位置，此时等离子体的作用区域整体处于分离区，故3h并非最佳控制位置。而在3.1h施加等离子体时，其右侧剪切力均为正值，说明分离区完全在等离子体流动控制区域的左侧，故3.1h即为5 m/s来流风速对应的最佳控制位置。图10给出了来流风速为5 m/s时等离子体处于最佳控制位置的速度矢量图。

图10 来流风速为5 m/s时、在3.1h处施加等离子体的速度矢量图

通过图10和图7的对比可以看出，施加等离子体流动控制时，可以使台阶后部流动分离(分离区)区域减小，再附着点前移。为精确描述再附着点的前移量，做出底面中线的壁面剪切力图，如图11所示。

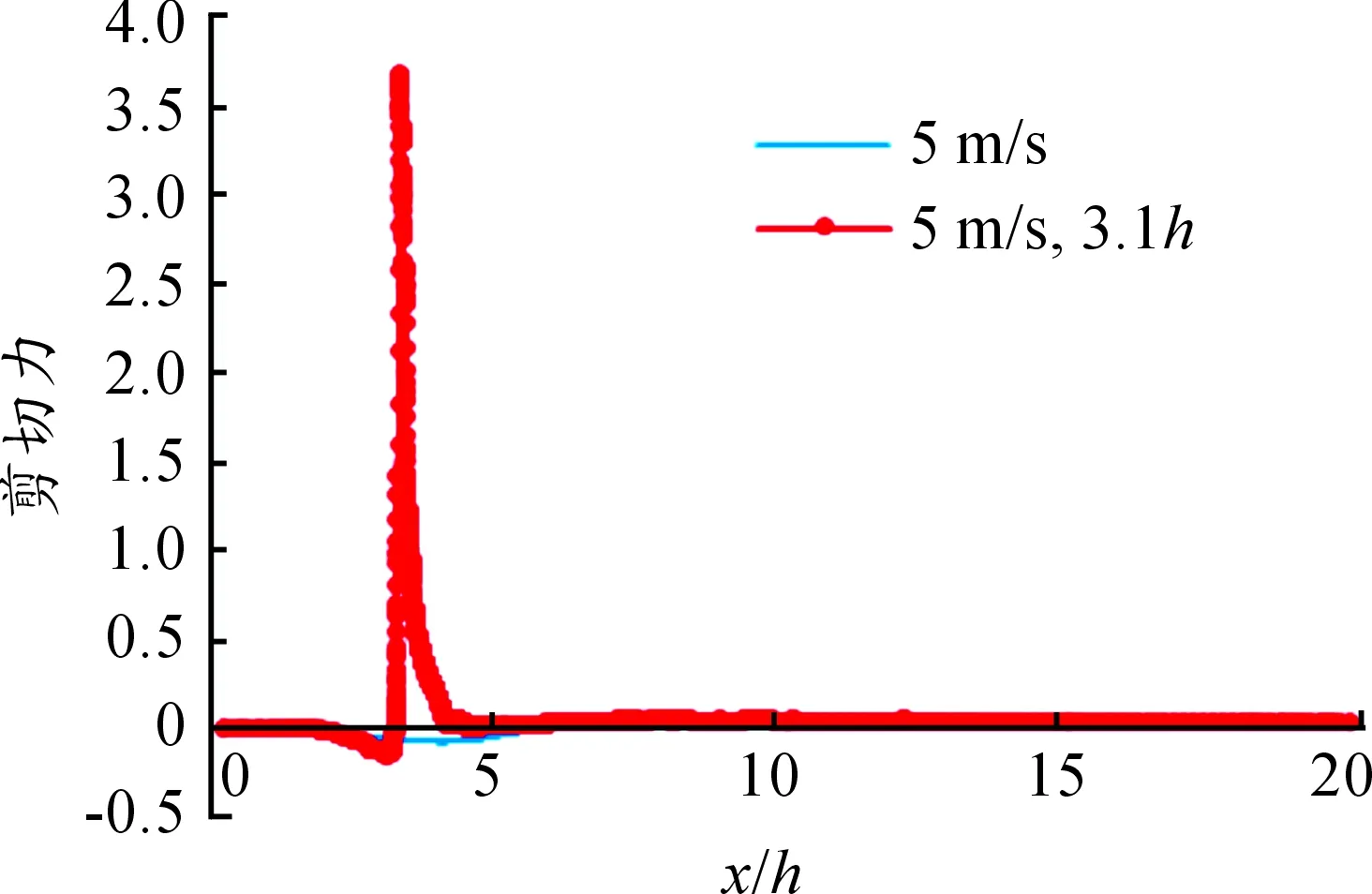
图11 风速5 m/s、3.1h处施加等离子体剪切力

图中蓝线代表不施加等离子体流动控制时底面中线剪切力，红线代表在最佳位置施加等离子体时底面中线剪切力。由剪切力图可以发现，只有在加载等离子体附近，数据点出现波动，其余数据点几乎重合，说明仿真重复性良好；由剪应力图得到此时再附着点为x/h=3.306，与基础工况x/h=5.547 3相比，将再附着位置提前45.27%。

接着进行风速为10、15、20 m/s时等离子体的控制效果和最佳控制位置的研究。采用本文所述方法，并将各风速下最佳控制位置和再附着点位置进行整理，结果如表3所示。

可以看出，不同来流风速时，等离子体对流动的控制都有不错的效果；在等离子体电压等参数不变的情况下，控制效果随风速增加而变弱。

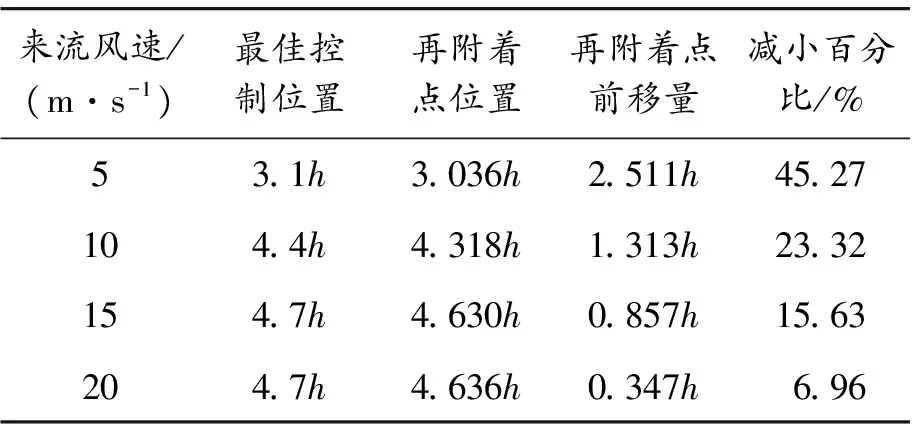
表3 不同来流风速下等离子体最佳控制效果

3.2 激励电压对等离子体控制的影响

保持风速为20 m/s不变，电压由2.262 7 kV增加为3、4、5 kV，采用本文所述方式探究等离子体控制效果和最佳控制位置。将结果进行整理，如表4所示。

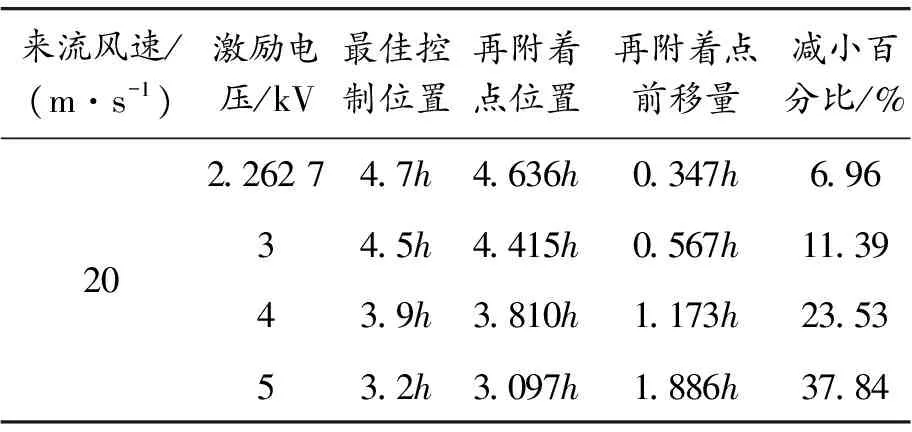
表4 不同激励电压时等离子体最佳控制效果

可以看出，增加等离子体激励电压，再附着点位置明显提前；当激励电压增加到5 kV时，最佳控制位置为x/h=3.2，此时再附着点位置为3.097h，与20 m/s工况的4.983h相比提前了1.886h，将分离区长度减小37.84%。

4 结论

运用Fluent软件和SSTk-ω模型对等离子体控制下后台阶流动进行了数值模拟仿真分析，得到如下结论：

1) 来流风速一定时，等离子体流动控制可明显减小后台阶流动的再附着长度；来流风速不同时，存在最佳控制位置；当来流风速为5 m/s时，等离子体对后台阶流动控制效果最好，可将再附着点位置提前45.27%。

2) 当增加激励电压时，可进一步减小后台阶流动的再附着点位置，其中当来流风速为20 m/s、激励电压增加至5 kV时，可将再附着点位置提前37.84%。