基于CoDeSys的全向移动机器人控制系统设计

，，，

(浙江工业大学 信息工程学院，浙江 杭州 310023)

移动机器人以其具有灵活性、提高生产效率和改善劳动条件等优点而得到广泛应用[1]。随着社会的不断发展，人们对移动机器人的灵活性及智能提出了更高的要求，要求移动机器人能在一定的范围内安全运动，完成特定的任务，增强移动机器人对环境的适应能力[2]。

因此，近年来移动机器人成为机器人研究领域的中心之一[3]。移动机器人的移动机构有多种形式，常见的有轮式、腿式和复合式等，这些移动机器人之中，轮式移动机器人由于设计与控制简单，被广泛采用[4]。当移动机器人需要在狭窄、拥挤或需要避障的环境中运行时，机器人的全向移动能力就变得至关重要[5]。全向移动机器人是一类典型的移动机器人系统，可以在不改变车体的情况下，实现从当前位置向任意方向的运动，而且可以零半径转向，且有平面上沿X，Y轴平动和绕Z轴转动的3个自由度[6]。目前，许多学者都对全向移动机器人做了大量的研究工作，Jamali等[7]以Mecanum轮式的全向移动机器人为对象，研究它的建模与仿真，并设计了三个独立的模糊控制器来完成机器人的位置和角度跟踪。Oftadeh等[8-11]采用四轮全向移动平台，针对移动机器人在奇异点附近存在无界的转向速度问题，设计了一种新的路径跟踪控制器，将机器人的车体线速度描述为车轮驱动和转向速度的函数，然后利用这些函数求出最大瞬时速度，使车轮速度保持在预定的界限之下。

当移动机器人进入奇异点及附近区域，车轮出现较大的转向速度，导致系统不稳定。一些方法是使机器人远离这些区域，但是这样会限制机器人的灵活性。笔者基于传统的路径跟踪控制器，设计了一种全局稳定的路径跟踪控制器。首先搭建一台对角驱动的四轮全向移动机器人。其次，根据车体期望位置-航向和实际位置-航向偏差信号，构建正定的Lyapunov函数，设计适应车体线速度的反馈控制律，使闭环控制系统下的Lyapunov函数导数为负定，车体位置-航向在该控制律作用下跟踪上期望位置-航向。依据逆运动学约束，建立了车体最大速度与车轮牵引速度、转向速度之间的车体运动约束关系；在此基础上，选取车体最大线速度，规划车体线速度，使得车体以时间最优跟踪期望轨迹。最后，基于CoDeSys上位机进行实验，验证了算法的有效性和稳定性。

1 全向移动机器人结构设计

对于移动机器人的车轮布局，一般常用的布局主要分为三轮配置和四轮配置。四轮布局相对于三轮布局稳定性更好[12]。四轮布局如图1所示，一般可分为前轮驱动(图1a)、后轮驱动(图1b)和左右轮对角驱动(图1c)三种。对角驱动方式可使车辆具有横向移动的能力，提高车辆的灵活性[13]。所以笔者采用左右轮对角驱动(图1c)方式设计车辆底盘。

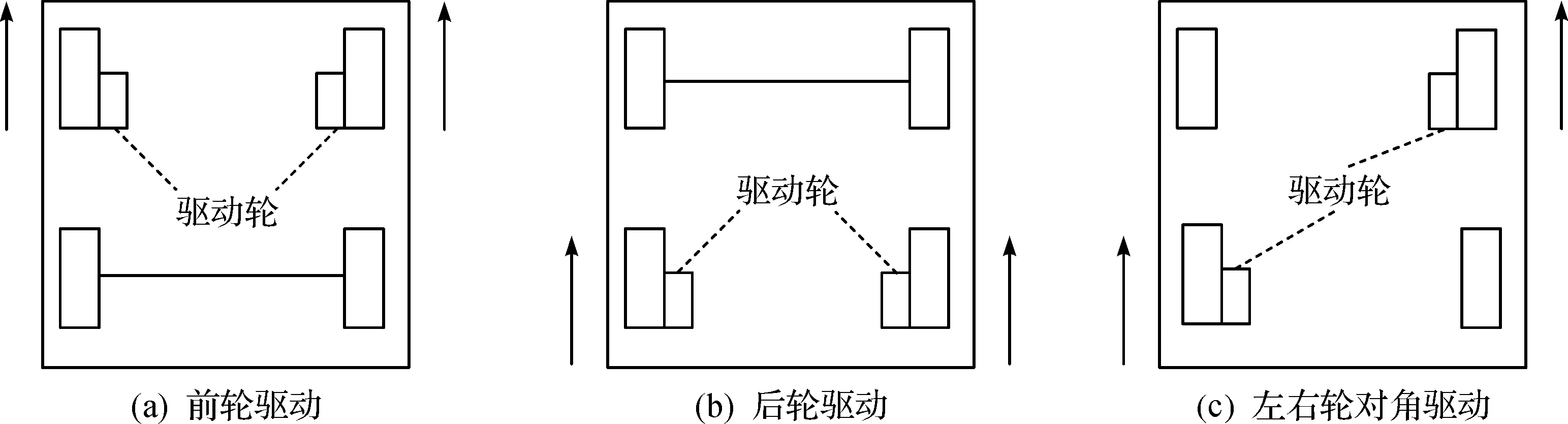
图1 四轮构型Fig.1 Four-wheel configuration

车轮选择意大利CFR舵轮。CFR舵轮具有体积小巧、操作简单和适应性强等优点。舵轮主要由一个牵引电机和一个转向电机组成，并配有两个增量式编码器。

小车电源选择磷酸铁锂电池。磷酸铁锂电池具有寿命长、使用安全、充电快速、耐高温和容量大等优点。驱动器选用RoboteQ双通道驱动器，该驱动器具有平稳、高精度的低速控制特性和良好的高速性能。控制器采用基于CoDeSys的运动控制器，并通过一个EtherCAT转CAN的数据网关转换器连接驱动器，实现对舵轮的控制。控制系统结构如图2所示。

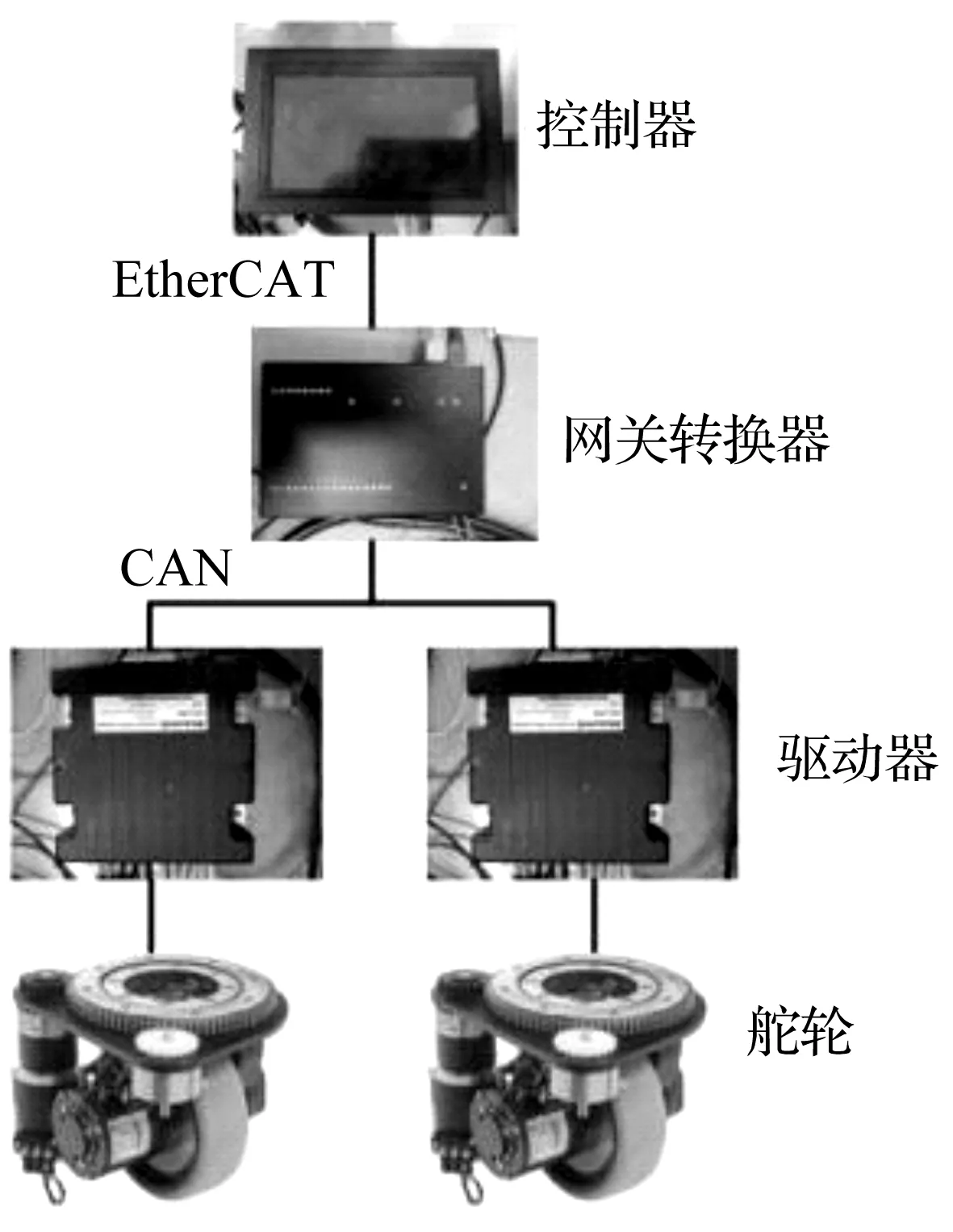
图2 控制系统结构图Fig.2 Control system structure diagram

在上位机CoDeSys软件上，使用结构化文本(ST)和连续功能图(CFC)编程语言，开发小车控制程序，然后下载到控制器。控制器运行程序，通过EtherCAT总线以线性拓扑结构的方式[14]，把数据传给从站网关转换器，网关转换器再把数据转化成CAN数据发给驱动器，然后驱动器分别给牵引电机和转向电机下发指令，控制电机的运转，从而控制车体的运动。控制流程图如图3所示。

图3 控制流程图Fig.3 Control flow chart

2 速度受限的移动机器人控制算法设计

如图4所示，坐标系{U}为世界坐标系，坐标系{Bd}和{T}分别为期望运动轨迹Pd(s)(s为自变量，表示轨迹弧长)上的移动车体坐标系和速度坐标系。{B}为移动车体坐标系，{Bv}移动车体速度坐标系，{B1}车轮1坐标系。p为车体期望位置，θd为期望航向角，θd(s)为航向轮廓，vt，ψt分别为期望线速度大小和方向。q为移动车体实际位置，θb为实际航向角，v，ψv分别为线速度大小和方向，ωb为车体角速度。l1，l2为车体中心点到驱动轮的距离，φi，vi分别为车轮的角度和速度。

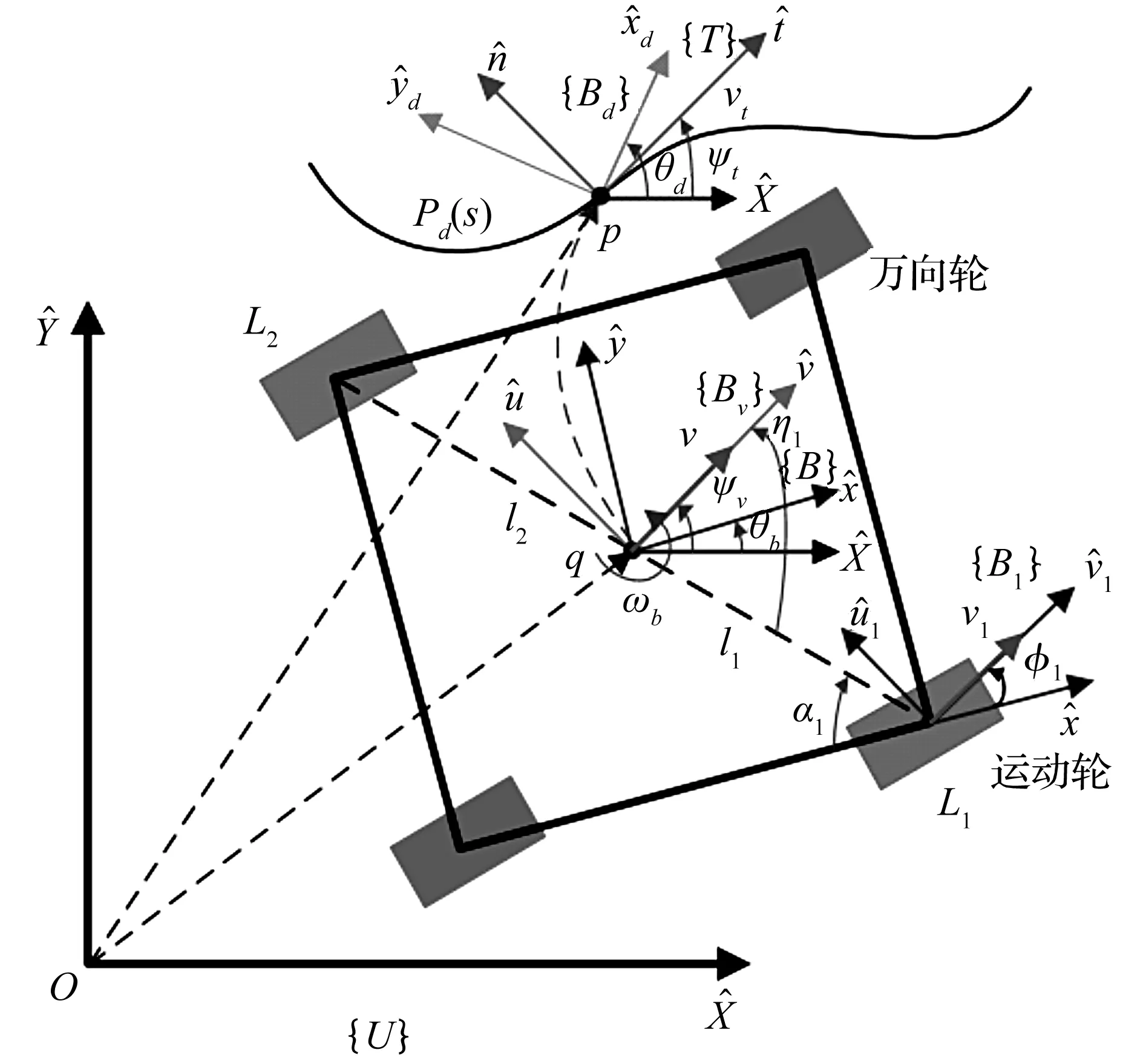
图4 路径跟踪示意图及参数Fig.4 Trajectory tracking schematics and parameters

2.1 运动学模型

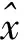
(1)

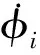
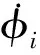
2.2 控制律设计

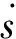
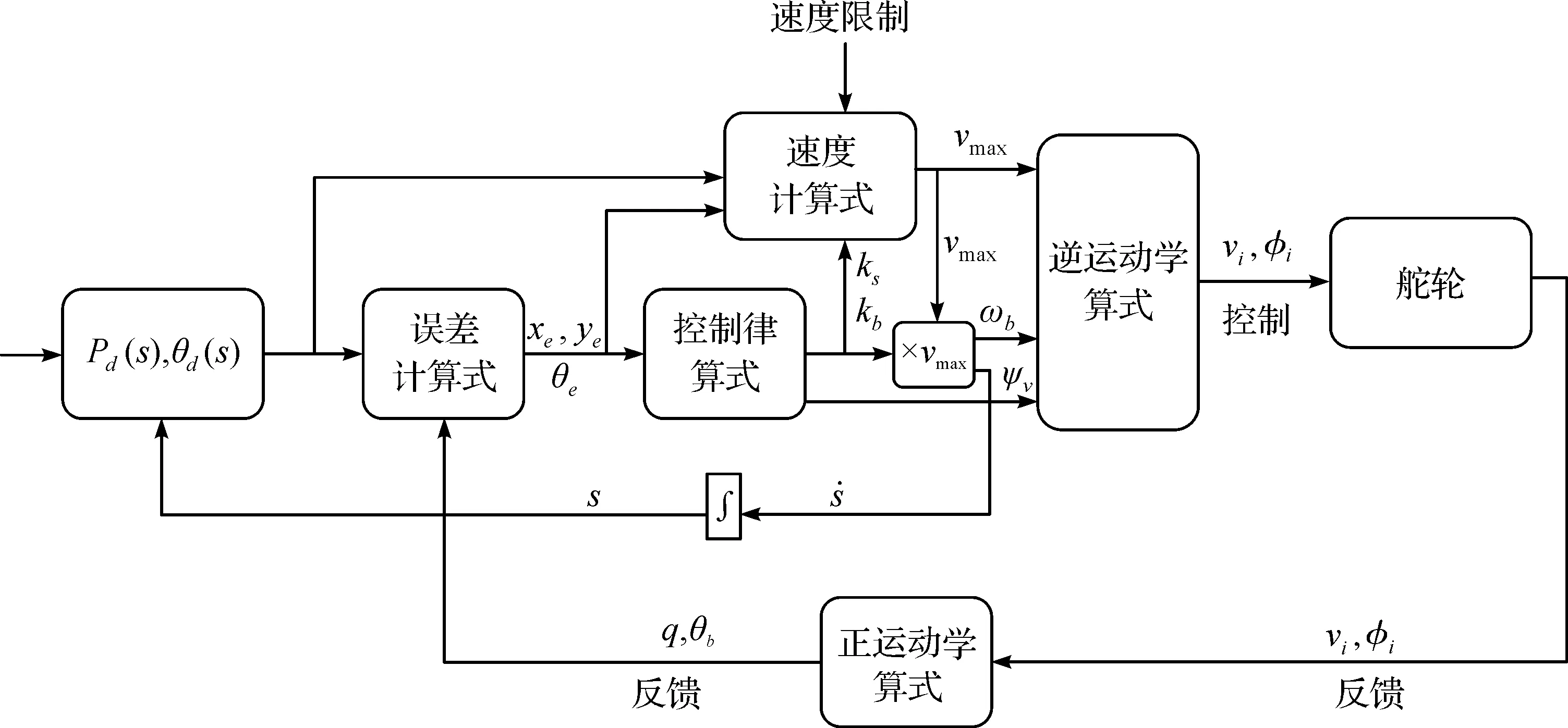
图5 系统示意框图Fig.5 System schematic block diagram

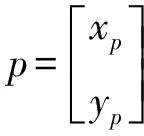
移动车运动偏差方程为

(2)

θe=θd-θb

(3)

对式(2，3)求导可得

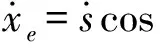
(4)

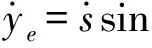
(5)

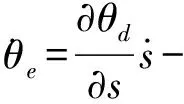
(6)

为系统设计相应的Lyapunov函数，然后利用Lyapunov函数的稳定性判定条件，得出移动机器人轨迹跟踪的控制律[15]。设运动学控制律的Lyapunov函数为

(7)

对式(7)求导并将式(4～6)代入得

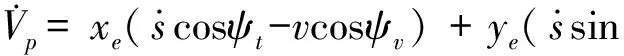
(8)

假设

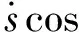
(9)

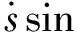
(10)

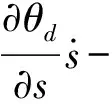
(11)

可得反馈控制律为

ψv=ψt+arcsin(k2yecosψt-
k1xesinψt)=ψt+arcsinρ

(12)

(13)

(14)

将反馈控制律式(12～14)代入式(8)，可得

(15)

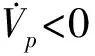
将式(12～14)代入式(4～6)得

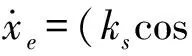
(16)

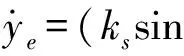
(17)

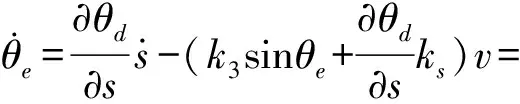
(18)

根据运动学约束方程式(1)，并对其两边求导可得

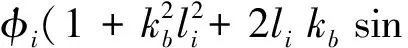
(19)

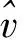
(20)

(21)

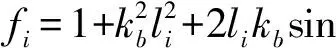
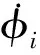
(22)

当v取vmax时，小车以可行的最大速度运动，所用时间最短，实现时间最优控制。

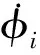
2.3 仿真实验

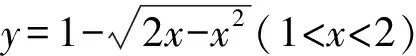
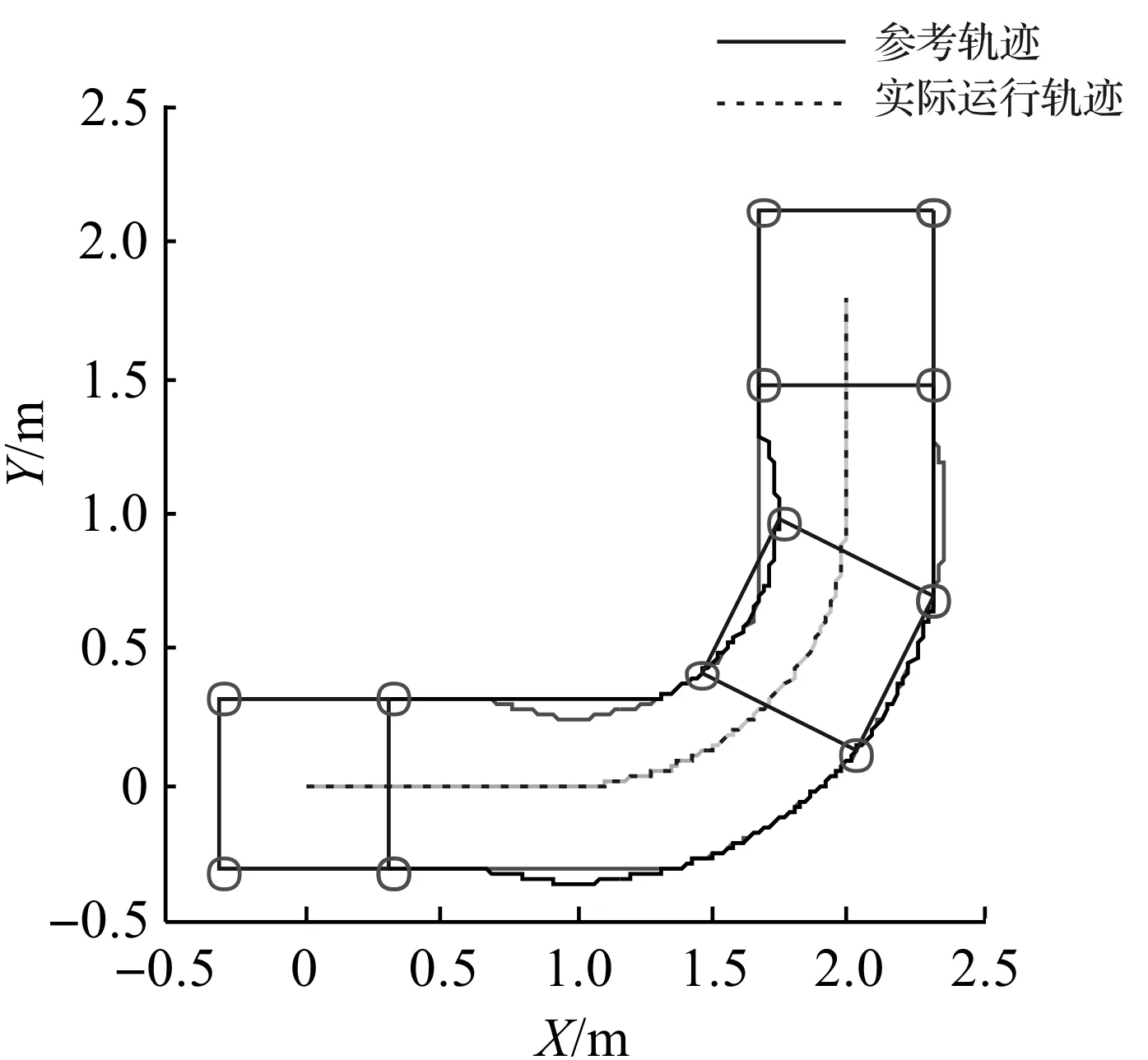
图6 轨迹跟踪示意图Fig.6 Trajectory tracking schematic.

根据仿真结果可知：基于Lyapunov稳定性原理设计的一种适应车体线速度的反馈控制律，可使移动机器人跟踪上期望轨迹，验证了算法的有效性。

3 算法实现与实验分析

3.1 算法实现

在CoDeSys上位机上使用结构化文本(ST)和连续功能图(CFC)编程语言开发程序。主程序主要由四部分组成。由算法中误差计算模块、速度计算模块及控制律模块组构成控制器功能块(Controller)，用于参考轨迹的规划及机器人运行轨迹控制；由逆运动学模块构成逆运动学功能块(InverseKinematic)，用于运动的分解；驱动功能块(Driver)用于数据的下发及采集，驱动机器人运动；由正运动学模块构成正运动学功能块(ForwardKinematic)，根据反馈的数据计算出车体的实际位姿。如图7所示，由4 个功能块构成运动控制系统，实现对机器人的控制。

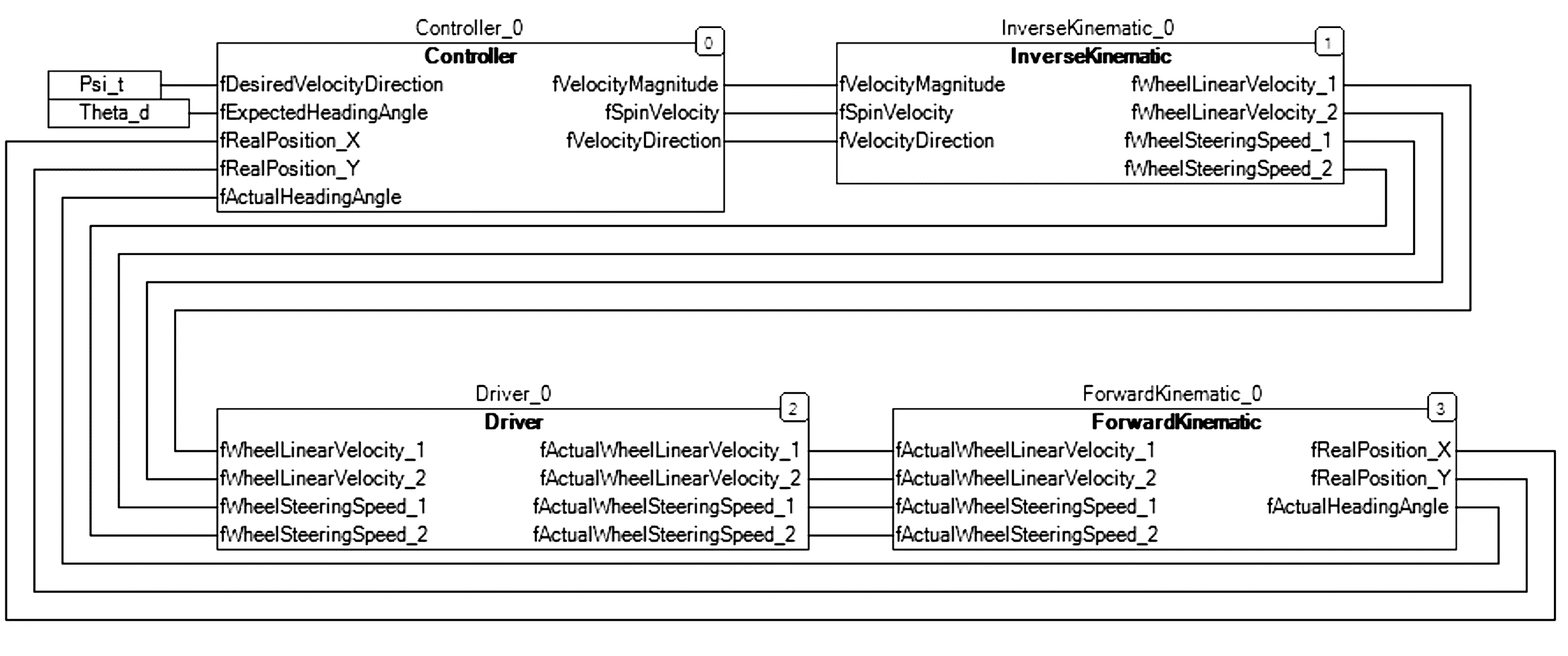
图7 主程序框图Fig.7 Frame of main program

3.2 实验分析

为验证控制算法的正确性，对系统进行实验验证。四轮全向移动机器人的参数如表1所示。

基于CoDeSys上位机进行实验，实验参考轨迹和仿真参考轨迹相同，实验结果如图8～10所示。

表1 机器人参数Table 1 Robot parameters

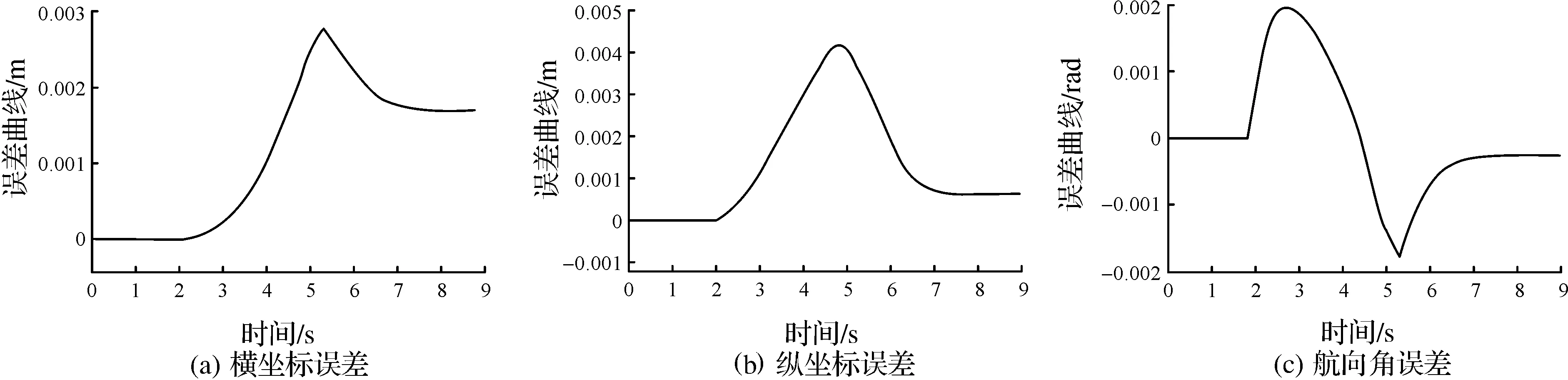
图8 车体位姿误差Fig.8 Body position and posture error

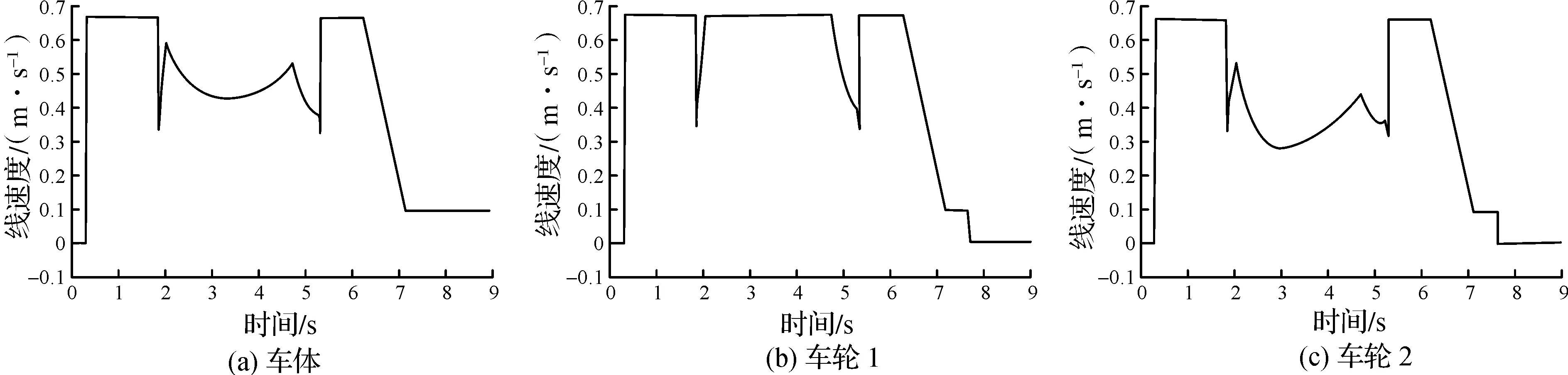
图9 车体和车轮线速度Fig.9 Car body and wheel linear velocity

图8显示了在进行轨迹跟踪时车体的位姿误差，可知车体基本跟踪上参考轨迹；图9显示了车体和车轮的线速度；图10显示了车轮的旋转速度。从图10中可以看出：在时间为1.8 s和4.6 s左右时，根据车轮最大转向速度，降低车体速度，从而使车轮转向速度保持在预定的极限以下。

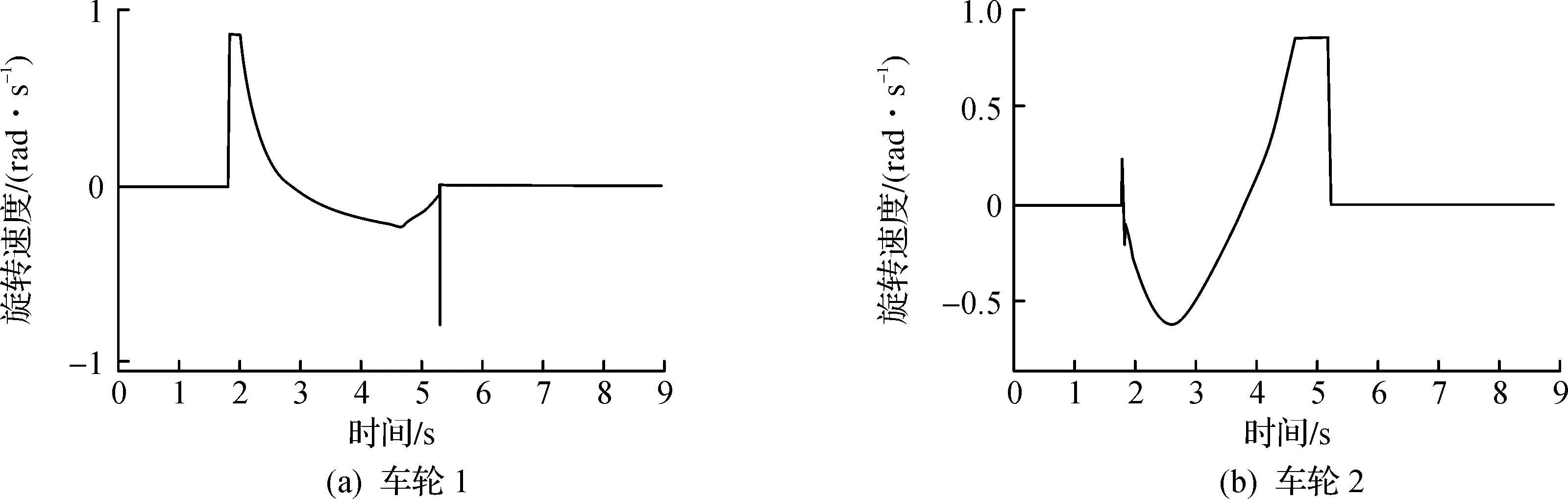
图10 车轮旋转速度Fig.10 Wheel steering speed

综合上述的实验结果可以得出：在该控制律的作用下，轮式移动机器人能够跟踪上设定的参考轨迹，并且在复杂运动过程中，车轮的驱动和转向速度均保持在预定值之下，证明了所设计的速度受限控制律的有效性和稳定性。

4 结 论

设计并搭建一台全向轮式移动机器人作为实验平台。根据Lyapunov函数稳定判据，设计了适应车体线速度的反馈控制律。基于运动学约束，对车体线速度进行规划，求出车体最大瞬时速度，使得无论机器人距离它的奇异点区域有多近或者多远，车轮的速度都保持在预定极限之下，解决因为奇异点状况造成的系统不稳定问题，并实现跟踪期望轨迹时间最优。在CoDeSys上位机上编写运动控制程序，实现了移动机器人对轨迹的跟踪，验证了控制律的有效性和稳定性。