多个连续性共同终点非劣效临床试验的样本量估计*

周憧憧 陆梦洁 刘玉秀,△ 陈 羽 刘甜甜 刘雅琦1, 占文强 赵施施

在许多临床试验中，由于病人对治疗的反应可能是多方面的，因此其疗效常常不能由单一的指标完全反映，而需要由一系列可能相关的指标才能综合反映出来，这就是所谓的共同终点(co-primary endpoints)。从统计推断意义上看，共同终点是指多个终点同时具有统计学意义，方可声称药物或者器械的有效性，此时采用的是联合检验，不需调整I类错误，但II类错误会随着终点个数的增加而膨胀[1-2]。近年来，随着多终点临床试验的开展日益增多，有关多个共同终点临床试验的样本量估计问题引起人们关注[3-6]。既往常按单个终点分别估计并选择最大值的方法，但该方法既没有考虑多终点间的相关性，也很难通过控制II类错误率发生达到预定的全局把握度[7]。2011年Suzu[8]等阐明了优效性临床试验多个相关终点作为共同终点的样本量估计方法，解决了多终点间非独立以及保护全局把握度的问题。本文将在优效性临床试验样本量估计方法的基础上，扩展提出非劣效临床试验多个连续性共同终点的样本量估计方法，并结合临床麻醉学中一个重复测量终点非劣效临床试验的实际案例，在不同的参数设置下，进行样本量估计和Monte-Carlo模拟验证。

多个连续性共同终点优效性临床试验样本量估计方法

在随机对照临床试验中，假定试验组有n1例，对照组有n2例。假定有K个共同终点且服从K元正态分布(K≥2)。试验组n1例受试者的响应值记为Y1jk，j=1,…,n1，对照组n2例受试者的响应值记为Y2jk，j=1,…,n2，k=1,…,K。将其写成向量形式即为：

Y1j=(Y1j1,…,Y1jK)T，Y2j=(Y2j1,…,Y2jK)T

两者均服从K元正态分布，其均向量分别为：

E[Y1j]=μ1=(μ11,…,μ1K)T，E[Y2j]=μ2=(μ21,…,μ2K)T，

协方差阵为∑：

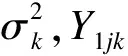
在优效性临床试验中，关注的是两组均数的差值，假设各终点指标均为高优指标。

δk=μ1k-μ2k,δk>0 代表诊疗有益

进行优效性假设：

H0:δk≤0 ，只要有一个k满足

H1:δk>0 ，所有k均需要满足

基于上述的假设，当且仅当所有单个终点均在检验水准α下被拒绝时其原假设H0才能被拒绝，其拒绝域是K个终点拒绝域的交集，故多个共同终点的检验属于交并检验(intersection-union test, IUT)。

1.方差已知的样本量估计方法

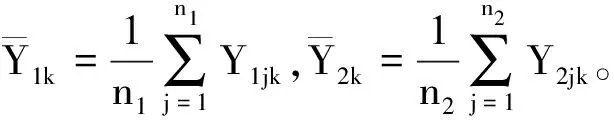
zα为标准正态分布下上100α%分位数，该式可以进一步转换为：

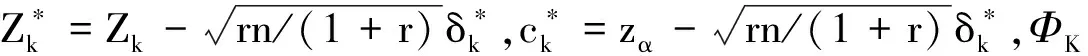
2.方差未知的样本量估计方法

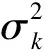
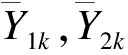
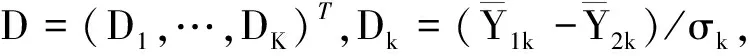
tα,n(r+1)-2为自由度为n(r+1)-2的t分布上100α%分位数，如果K=1，那么全局把握度1-β的计算将基于非中心t分布。当K≥2时，Tk并不是一个多元非中心t分布，因为wkk′是Wishart分布，而Wishart分布不属于多元gamma分布。因此重新定义的全局把握度1-β如下：

1-β=

ΦK是多元正态分布的累积函数，它的均向量为零向量，协方差阵为ρ。上式需要通过Monte-Carlo模拟计算，按照给定的自由度和协方差矩阵，随机产生Wishart分布，进而获得ΦK的期望作为全局把握度[3]。

多个共同终点非劣效临床试验样本量估计方法

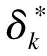
μ1k表示试验组第k个终点的总体均数，μ2k表示对照组第k个终点的总体均数。Δk(Δk>0)表示第k个终点的非劣效界值，σk表示第k个终点试验组或者对照组的标准差(这里设定试验组和对照组标准差相同，如果不同则为两组的合并标准差)。

根据非劣效试验样本量估计的公式对单个终点分别计算样本量，其中试验组样本量计算公式为：

则对照组的样本量为rn1，总样本量为(1+r)n1[9-10]。选取K个样本量中的最大值作为初值，套用优效性试验样本量估计的迭代算法，即可获得非劣效试验的样本量估计结果。

案例分析

儿童腹股沟斜疝高位结扎术时间短，临床上通常采用插喉罩(laryngeal mask airway，LMA)静吸复合全麻，但是喉罩操作对新手存在难度，拔管时可能出现咬管、喉痉挛等不良事件，易发生插管部位疼痛、出血等并发症。某医院自主设计了新型通气设备(new mask airway,NMA)，希望该设备应用于此类儿童手术在效果上非劣于LMA麻醉方法。该非劣效临床试验主要考察的是通气数据潮气量(tidal volume，VT)，需要在多个时间点上均呈现出非劣效才可认定新型设备的非劣效性。根据预实验结果，假定在3个时间点上两组的VT相同，其均数±标准差分别为11.0±3.2，9.5±2.4，8.6±2.1，非劣效界值取对照组均数的15%，分别为1.65、1.425和1.29，若按照各时间点VT之间相关系数均为0.6(可允许不同)，则根据前面介绍的方法，在I类错误水平取0.025的条件下，每组用136例可达到80%的全局把握度。本文样本量计算基于R软件编程实现，部分程序代码见附录。

为了验证方法的正确性，我们基于本例非劣效临床试验基本框架进行了Monte-Carlo模拟验证。假定两组的总体均数相同，按照不同的非劣效界值(分别取对照组均数的10%、15%和20%，见表1)、终点间不同的相关系数(0、0.2、0.4、0.6、0.8、1.0)、不同的I类错误水平(0.025、0.05)下的不同参数设定，按照本文介绍的方法进行了全局把握度为80%的样本量估计，并在相应样本量之下，按照不同的参数设定随机产生多元正态分布，模拟10000次，进行交并检验，进而求算出全局把握度(结果见表2)，通过该模拟把握度与预设把握度的比较验证方法的正确性。

表1 某新型通气设备非劣效界值Δ设置情况

由表2可见，多个共同终点考虑下的样本量估计结果，在不同的参数设定下所模拟获得的全局把握度与预设把握度极为接近，在80%的预设把握度下最多不超过1.5%，较好地验证了本文方法的正确性。从具体的样本量行为还可看到，多个共同终点的样本量与相关系数、I错误水平和非劣效界值均直接有关，随着终点间相关系数的增大而减小，随着非劣效界值减小而增大，I类错误水平越小，样本量越大。此外，在各终点完全相关(相关系数为1)时，多个共同终点考虑下的样本量与按单个终点计算的最大样本量相当，其他情况下均为前者大于后者。这意味着，在各个终点完全相关时，取单个终点的最大样本量可以达到预设的全局把握度，而在其他情况下，即使取最大样本量也不能达到预设的全局把握度。

讨 论

本文利用Suzu等提出的多个连续性共同终点优效性临床试验样本量估计的方法，在阐明其样本量估计的理论基础上，扩展提出关于多个连续分布共同终点非劣效临床试验的样本量估计方法。结合临床麻醉学中一个重复测量终点非劣效临床试验的实际案例，基于其预试验的相关结果，在不同的Ⅰ类错误率水平、各重复测量间不同的相关系数、不同的非劣效界值设定下，估计了满足一定的全局把握度(例如80%)的样本量，并借助Monte-Carlo模拟方法验证了方法的正确性。此外，我们还对试验组与对照组均数差值不全为0的情况(均大于0、均小于0、不全为0)估计的样本量进行了不同参数设定下的模拟验证，其全局把握度均能与预设把握度高度吻合，验证了本文方法的普适性。实例及模拟验证中采用的样本量估计方法为按照方差已知的情形而进行的，我们同时也按照方差未知的情行进行了计算和模拟，其结果与方差已知情形相差甚微，在本实例的参数设定框架下仅相差1例。相关的验证结果因篇幅所限未列出。本文介绍的样本量估计方法具有严密的统计理论基础，能较好地保护全局把握度，具有较强的实用价值，可望为多个连续分布共同终点非劣效临床试验的样本量估计提供有力的方法学支持。

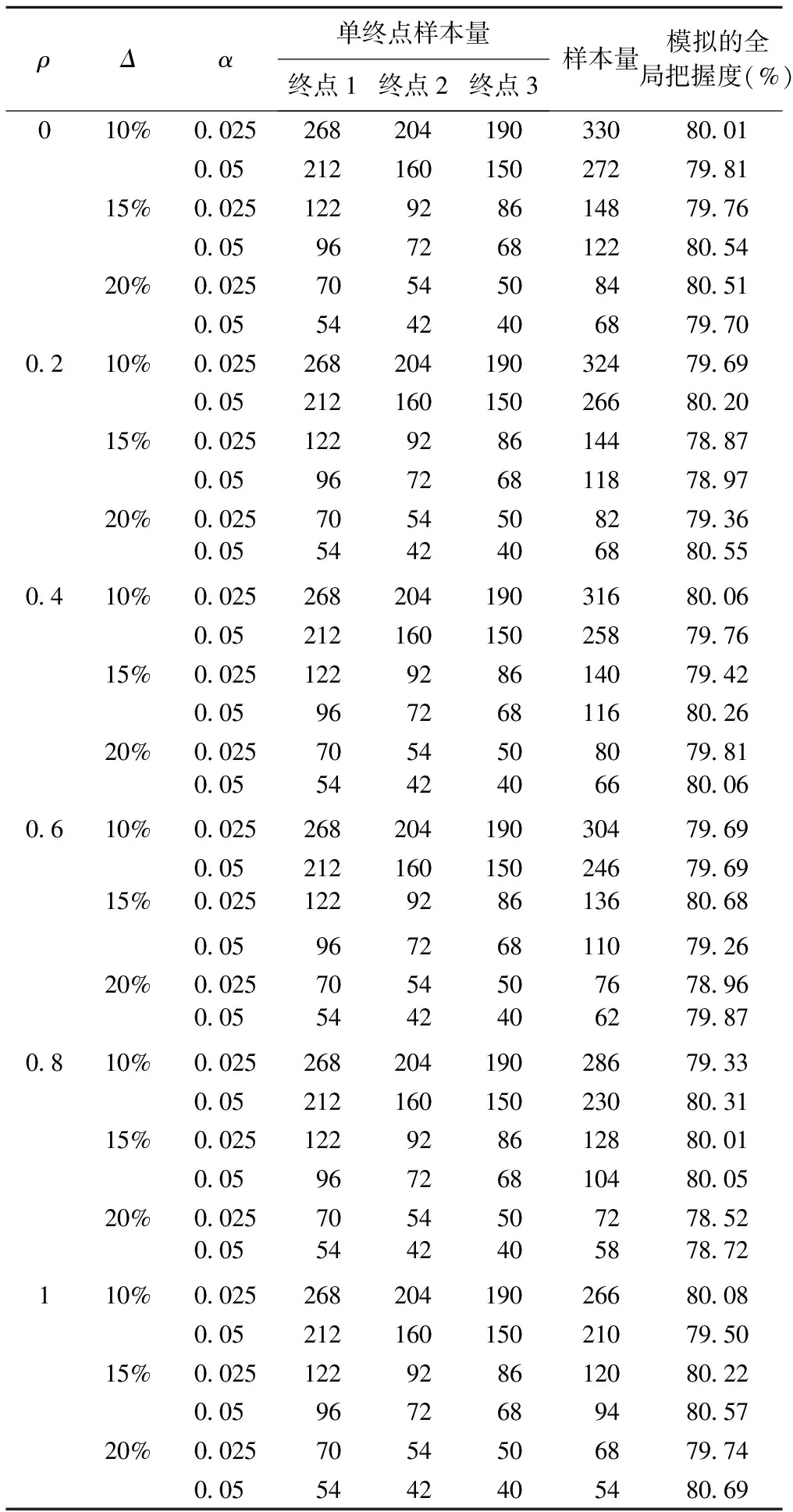
表2 全局把握度为80%不同参数设定下的样本量估计及Monte-Carlo模拟结果及

对于临床试验中存在多个共同终点的情形，传统的确定样本量的方法是对II类错误水平进行校正[11]，然后按各单个主要终点分别计算所需的样本量，并从中选取最大值作为最终样本量，以保护全局把握度。该方法没有考虑各终点间的相关性，所给出的最终样本量为单个终点样本量中的最大值，必然造成其他终点把握度的膨胀，从而导致全局把握度的浪费。而如果不校正II类错误水平，选取单个终点样本量中的最大值作为最终样本量，则全局把握度明显不足。本文提出的方法很好地解决了此问题。

本文实例的终点为重复测量数据，似乎并不是典型的共同终点情形，但从研究目的和临床实际的角度上考虑，由于3个重复测量点均需要达到非劣效方可最终推断新型通气设备的非劣效性，恰巧符合共同终点的定义，因此完全可视为3个共同终点而采用本文介绍的样本量估计方法。无疑，该应用为重复测量临床试验样本量估计提供了一种新的思路。

值得注意的是，由于实际中相关系数一般是未知的，尽管可以从以往的文献中寻找或者通过预实验获得，但不能过于激进，宜采用相关系数的保守结果，以免全局把握度不足。鉴于多终点临床试验样本量估计的复杂性，有学者曾提出将多个终点合成为一个复合终点[12]，可一定程度上解决样本量估计和统计推断的问题，但在许多情况下该做法并不被接受。