基于XFEM的坝体损伤扩展模拟
刘江川,陈 超,李 燕
(1.长春工程学院水利与环境工程学院,长春 130012;2.吉林省水利电力工程物理级仿真与安全创新中心,长春 130012)
0 引言
有限元法[1](Finite Element Method,FEM)将结构离散化,用节点将有限个简单单元相互连接来表示复杂结构,再根据平衡、变形协调条件对结构进行综合求解。但是,传统有限元对工程中存在的不连续问题的处理却不尽人意,比如裂缝、杂质、孔隙等。
一般而言,结构在外界作用下出现不连续问题是不可避免的,而不连续部位对结构的整体稳定和破坏起控制作用,并且难以计算和监控。Beleytachko教授提出的扩展有限元法[1](Extended Finite Element Method,XFEM),解决了不连续问题的有限元计算,可以称作解决不连续问题最有效的数值方法。XFEM在常规有限元法的位移模式中加入特定函数反映不连续面[2],不连续面与计算网格是相互独立的,裂纹的几何界面不依赖于单元边界,裂纹扩展过程中也不需要重新划分网格单元[3]
本文结合扩展有限元法和塑性损伤模型[3],以Koyna大坝为例,模拟在强震作用下坝体混凝土的损伤破坏过程,研究在强震作用下,混凝土重力坝的裂缝扩展情况[1]。
1 混凝土塑性损伤模型
1.1 应力—应变关系
在混凝土塑性损伤模型中,假定混凝土的破坏主要是由受拉、受压导致材料破裂形成的,屈服面和破坏面的发展是由拉压等效塑性应变控制的[4]。在处于弹性阶段时,采用线弹性模型表达混凝土的力学性能[5],当混凝土进入塑性损伤阶段,用损伤因子和初始无损弹性模量表达受到损伤后混凝土的弹性模量[6]:
E=(1-d)E0,
(1)
式中:E0为混凝土的初始无损弹性模量;d为混凝土的损伤因子。
1.2 损伤因子
材料在加载条件下,内凝聚力不断减弱,由于微缺陷的产生和发展,导致单元发生破坏,引起材料逐步劣化,这就是“损伤”。而损伤常与弹性、塑性、弹塑性材料相结合,作为一种描述劣化程度的因素。我们在研究混凝土应力和应变关系时,常采用损伤因子的概念来描述卸载过程中材料的刚度退化等现象[7]。损伤因子的数值按式(2)计算:
(2)
式中:K为混凝土的应力状态;t,c分别表示受拉、受压状态;ein为混凝土在拉压情况下非弹性阶段的应变;b为塑性应变比非弹性应变[8],当混凝土受压时,取0.135~0.17,当混凝土受拉时,取0.15~0.195。
2 建立有限元模型
2.1 工程概况
1967年12月10日,Koyna大坝附近发生6.7级地震,连续地震45 s,导致坝体和水电站建筑严重受损,当地居民死伤很多,并造成26万人流离失所。Koyna大坝坝型为混凝土重力坝,最大坝高为103.00 m,底宽70.00 m,地震发生时的坝前水深为91.50 m,Koyna大坝相关材料物理力学参数见表1。

表1 Koyna大坝材料的物理力学参数
2.2 建模概况
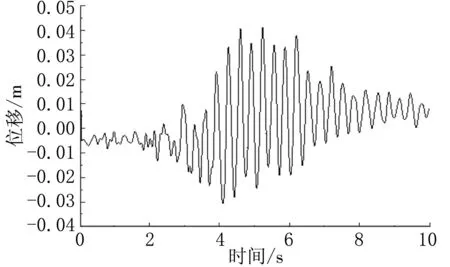
地震波采用Koyna地震的水平与竖向记录值,分别定义顺河向和垂直向为作用方向,Koyna地震的地震波如图1所示。假设基础为刚性,研究坝体在双向地震波共同作用下的非线性响应。计算荷载为:混凝土坝体自重+地震发生时的上下游静水压力+动水压力+地震。
3 结果分析
3.1 反应谱法与时程法
为了研究坝体在地震荷载下的应力变形分布[9],分别用反应谱法和时程法进行动力分析,两种方法的应力分布如图2所示。在坝高约66 m处,明显出现了拉应力集中区,在地震作用下,上游面的拉应力超过了4 MPa,下游坝面折坡处的拉应力超过7 MPa,坝踵处的局部应力超过了3 MPa[9],地震下坝体产生的拉应力大于混凝土的抗拉强度2.90 MPa,坝体将出现裂缝,有限元分析中的最大压应力<13 MPa,抗压强度满足要求。
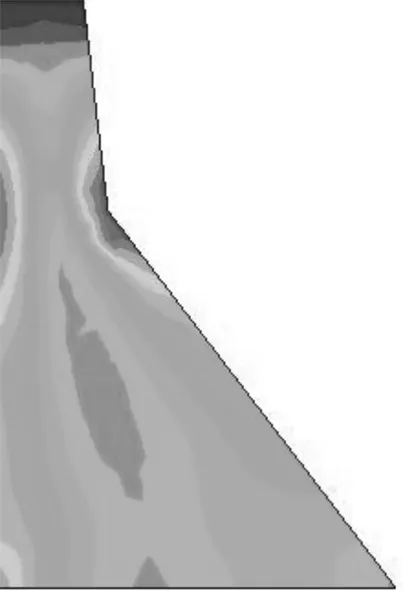
(a)反应谱法
在地震作用下,坝踵处首先出现拉应力损伤,随着地震的进行,损伤区逐渐上移,在T=3.88 s时,下游折坡处出现拉应力损伤区,损伤因子为0.25;在T=4.36 s时,损伤区从下游折坡处逐渐向上游面发展,折坡处损伤因子为0.56;在T=5.62 s时,下游折坡处损伤因子达到0.83,之后损伤区不再发展,这表明损伤区在坝体上部形成贯穿裂缝,拉应力损伤分布如图3所示。

(a)T=3.88 s
坝顶上游A点水平和竖直向位移时程曲线如图4所示。
(a)水平位移
位移时程曲线表明该点水平和竖直位移在5.0 s左右达到顶峰,6 s后开始位移减小。这说明随着裂缝的扩展,裂缝以上部位坝体受地震作用相对减小[9]。
3.2 扩展有限元法分析
用扩展有限元法对地震作用下的坝体裂纹扩展进行模拟,裂纹扩展过程和应力分布如图5~6所示。在T=3.67 s时,大坝下游面折坡处首先出现应力集中现象,应力值达到4.38 MPa,坝体进入裂纹扩展的初始阶段;在T=4.32 s时,裂纹逐渐向上游坝面发展,最大应力在裂缝缝尖处,并且上游坝面也开始出现应力集中现象;在T=5.62 s时,裂缝继续扩展,上游坝面应力进一步集中,直至裂缝贯穿整个坝面,缝尖应力达到8.91 MPa。

(a)T=3.67 s

(a)T=3.67 s
通过坝体混凝土裂纹扩展的情况,在坝下游折坡面首先出现应力集中且形成裂纹,随着裂纹向上游扩展,应力集中也是随着裂纹进一步扩展。裂缝的发展和混凝土损伤因子分布规律大致相同,这也验证了XFEM法计算结果具有较高的精确度。
4 结论
1)用XFEM模拟的Koyna大坝坝体混凝土损伤和裂缝扩展状况与Koyna大坝的实际破坏情况相一致,验证了XFEM分析不连续问题的有效性。
2)采用XFEM分析,能真实模拟裂缝的发展状态,裂缝可从单元内部断开,不依赖单元边界,计算结果精确度较高,并且不需要预留单元,减少了单元数目,还缩短了计算时长,计算结果满足工程分析的一般需求,可为复杂的大型结构分析提供借鉴。
3)在地震作用力下,坝体产生较大的拉应力,而混凝土抗拉强度较小,在大坝下游面折坡处首先发生裂缝,并逐渐向上游面扩展,直到贯穿整个坝体。

