基于卡尔曼滤波的汽轮机参数估计应用

毛朋涛

摘要：针对火力发电中汽轮机健康参数估计问题，研究了一种非线性卡尔曼滤波估计方法，比较了扩展卡尔曼滤波（EKF）和无味卡尔曼滤波（UKF）两种方法对参数估计效果，最终本文选取EKF对实际运动轨迹和期望运动轨迹进行研究。结果表明：扩展卡尔曼滤波能够很好地对参数进行估计，是一种实用的非线性参数估计方法。

关键词：卡尔曼滤波;汽轮机;参数估计

中图分类号：TP311      文献标识码：A      文章编号：1009-3044（2019）02-0254-02

1 引言

汽轮机性能参数估计作为火力发电健康管理系统重要内容，为其健康评估、维修计划制定提供依据，当前对汽轮机故障诊断采用的技术主要为：基于模型诊断、基于信号处理、基于专家知识库和基于机器学习的，其中基于模型诊断技术通过诊断逻辑实现故障判断和预测，广泛应用于汽轮机的健康管理中[1-2]。

在参数估计当中，很难找到一种严格的递推滤波算法，通常用近似方法去解决非线性滤波的问题。一类方法是寻找非线性函数的线性近似，线性化非线性模型：通过泰勒展开近似得到了扩展尔曼滤波（EKF），通过插值多项式近似得到了差分滤波（DDF）[3]。另一类方法是基于近似非线性函数的概率分布比近似其函数本身更容易的思想，通过UT 变换选择一组确定的点集来表征状态的统计特性（如均值和方差等），能直接应用非线性模型来求解，即无味卡尔曼滤波（UKF）[4]。后者计算较长，实时性较差，为此本文选择第一类方法中的扩展卡尔曼滤波方法对汽轮机进行参数估计。

本文選择扩展卡尔曼滤波并将其应用在汽轮机健康参数估计上，首先，建立汽轮机旋转运动轨迹模型;其次，运用EKF对模型进行跟踪仿真，最后给出仿真结果。

2 汽轮机模型

本文所用汽轮机非线性部件级模型，是根据非线性气动热力学方程描述对象，利用汽轮机连续、功率平衡建立汽轮机非线性动力学工作方程，实现对其动静态仿真和期望轨迹的追踪，某汽轮机在稳定工作点附近的模型为[5]：

[Δxk+1=f（Δxk，Δuk）+wkΔyk=H（Δxk，Δuk）+vk]                       （1）

其中，控制变量[Δu=[Δwf，ΔVS，ΔVB]]，[wf]为汽轮机进气量，[VB]为可调放气活门，[VS]为可调间隙，x为反映汽轮机工作状态变量，包括转速、部件效率和流量的参数。本文选取的健康参数有高压气机效率、流量退化量和能效，因此可得[Δx=[ΔNl，ΔNh，Δη，Δw]];输出参数[Δyk=[ΔNl，ΔNh，ΔT，ΔP]]，分别为低压转速、高压转速、高压气机进口温度和高压气机出口压力;[wk，vk]为互不相关高斯白噪声，其协方差矩阵分别为Q和R。[f（·），H（·）]表示汽轮机工作过程的非线性函数。汽轮机在工作过程中由于腐蚀或者卡滞等因素，都会表现为健康参数突变。

3 基于卡尔曼滤波器的参数设计

3.1 扩展卡尔曼滤波器设计

EKF将非线性系统在状态估计值附近作泰勒展开，取其一阶截断作为原状态方程和观测方程的近似式实现线性化，然后对线性化后的系统采用卡尔曼滤波进行状态估计。

对于形如式（1）的系统，首先根据上一时刻的状态估计值[xk-1]及状态一步预测值[xk|k-1]构造雅克比矩阵[6]：

[Fk|k-1=?f（xk，k）?xk|xk=xk-1=?f1（xk，k）?x1，k…?f1（xk，k）?xn，k????fn（xk，k）?x1，k…?fn（xk，k）?xn，kxk=xk-1]                     （2）

[Gk=?g（xk，k）?xk|xk=xk-1=?g1（xk，k）?x1，k…?g1（xk，k）?xn，k????gm（xk，k）?x1，k…?gm（xk，k）?xn，kxk=xk-1]              （3）

系统状态的均值与方差阵一步预测为：

[xk|k-1=f（xk-1，k-1）]                      （4）

[Pk|k-1=Fk，k-1Pk-1FTk，k-1+Qk-1]               （5）

在接收到最新观测数据[yk]后，对[xk|k-1]和[Pk|k-1]进行修正，分别为：

[xk=xk|k-1+Kk[yk-g（xk|k-1，k）]]               （6）

[Pk=1-KkGkKk|k-11-KkGkT+KkRv，kKTk]     （7）

式中 [Kk]滤波增益矩阵，计算公式为：

[Kk=Pk|k-1GTk[GkPk|k-1GTk+Rv，k]-1]           （8）

由式（2）～式（8）构成了扩展卡尔曼滤波算法的递推公式，那么对应于递推贝叶斯估计算法用扩展卡尔曼递推算法中的状态量可以分别表示为：

[p（xk|Yk-1）=N（xk;xk|k-1，Pk|k-1）]             （9）

[p（xk|Yk）=N（xk;xk，Pk）]                    （10）

对于算式（1）中，利用上述扩展卡尔曼滤波进行展开，用该点的雅可比矩阵求取卡尔曼增益，然后再利用卡尔曼滤波方法进行估计，因此式（1）的扩展卡尔曼滤波过程为：

[Δxk，k-1=f（Δxk-1，Δuk-1）Δxk=Δxk，k-1+Kk（Δyk-H（Δxk，k-1，Δuk））]

（11）

3.2 无味卡尔曼滤波器设计

无味卡尔曼滤波器（UKF）是基于无味变换的非线性卡尔曼滤波器，通过构造加权样本点对参数估计，避免对非线性模型的线性化处理，可以直接用来对非线性系统状态进行估计，其过程如下[7]：

下面将根据[k-1]时刻的状态估计值[xk-1]和[Py-1]，给出求k 时刻的状态估计[xk]和[Py]的实现过程。

1） 根据[xk-1]和[Py-1]，构造Sigma 点[χk-1']，[ i=1，…，2n]。

2） 计算预测 Sigma 点和均值

[χk|k-1i=fk（χk-1i）]

[xk|k-1=i=02nW（m）iχk|k-1i]

[Pk|k-1=i=02nW（c）iχk|k-1i-xk|k-1χk|k-1i-xk|k-1T+Qw，k]

3）修正（測量更新）

[Yk|k-1i=g（χk-1i）]                        （12）

[yk|k-1=i=02nW（m）iYk|k-1i]

[Py，k=i=02nW（c）iYk|k-1i-yk|k-1Yk|k-1i-yk|k-1T+Rv，k]              （13）

[Pxy，k=i=02nW（c）iχk|k-1i-xk|k-1Yk|k-1i-yk|k-1T]

（14）

[Kk=Pxy，kP-1xy，k]

[xk=xk|k-1+Kk（yk-yk|k-1）]

[Pk=Pk|k-1-KkPy，kKTk]

通过上述两种滤波方式分析对比，发现卡尔曼滤波（EKF）算法具有计算简单、鲁棒性强等优点，而无味卡尔曼滤波虽然解决了滤波发散等问题，但是由于其需要多次调用非线性模型进行参数估计，所以计算时间较长，实时性较差，为了保证参数在线估计，本文选取卡尔曼滤波对汽轮机运行状态的参数进行评估，以此判断其所处的状态。

4 仿真实例

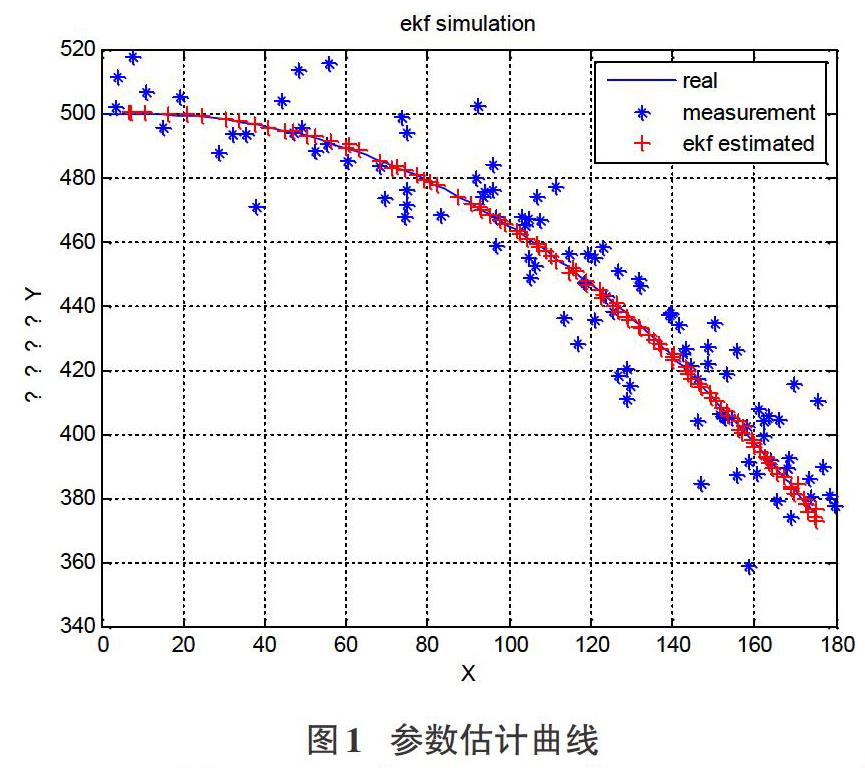
利用本文中的扩展卡尔曼滤波对某汽轮机旋转轨迹进行追踪，通过测量轴中心线实际的位移与期望轨迹进行对比，得出参数估计曲线如图1所示。

经分析可知，在仿真用时和模型调用次数方面，对于扩展卡尔曼滤波估计方法而言，由于再迭代计算过程中不需要多次调用非线性模型，所以在很短时间内就能追踪到轴中心的运动轨迹，这点区别于UKF，其调用次数最多，同时A，C矩阵的求取过程计算量也比较大，同样会影响仿真用时;特别是在后期，迭代到一定次数EFK预测轨迹于期望轨迹重合度很高。

5 结论

本文采用卡尔曼滤波方法对火力发电中汽轮机的运动参数进行估计和预测，同时对比了扩展卡尔曼滤波和无味卡尔曼滤波在参数估计过程中速度，结果表明无味卡尔曼滤波虽然在求解过程中采用灵活的周期更新算法，但是其计算时间较长，在实时性方面不如扩展卡尔曼滤波，因此扩展卡尔曼滤波是一种实时性较高的参数估计方法。

参考文献：

[1] 盛锴，魏乐，江效龙，寻新. 基于PSASP和Simulink的汽轮机调节系统建模与仿真校核[J]. 中国电力，2015，48（02）：1-6+26.

[2] 付文锋，杨新健，周兰欣，陈林霄，吴瑞康，王喆. 某600MW汽轮机低压末级排汽通道耦合流动三维数值模拟及其结构优化[J]. 中国电机工程学报，2014，34（14）：2267-2273.

[3] 赵洪山，田甜. 基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J]. 电网技术，2014，38（01）：188-192.

[4] 李江，王义伟，魏超，张鹏. 卡尔曼滤波理论在电力系统中的应用综述[J]. 电力系统保护与控制，2014，42（06）：135-144.

[5] 韩萍，桑威林，石庆研. 一种新型非线性卡尔曼滤波方法[J]. 仪器仪表学报，2015，36（03）：632-638.

[6] 夏楠，邱天爽，李景春，李书芳. 一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J]. 电子学报，2013，41（01）：148-152.

[7] 焉晓贞，罗清华. 基于卡尔曼滤波的动态传感数据流估计方法[J]. 仪器仪表学报，2013，34（08）：1847-1854.