基于ANSYSY软件软土地区地下车站抗震分析研究——以天津软土地区为例

王士军

（鹤壁职业技术学院 458030）

1 概述

近几十年来，地下结构的抗震问题日益受到重视，国内外学者也针地下结构问题做了很多研究工作。在实验研究中，振动台实验法因其能够较方便地进行材料选取和配比，且能直观地把握地下结构物的地震响应特性，而被广泛应用，但由于其资金和时间问题，目前尽可在少数地区部门可以实现振动台试验，而实际工程在时间上和资金上都需要能快速得出实验结果，为设计施工提供相应依据，通常采用模拟实验比较常见，ANSYS软件在建模是有多种方式可选，可以自顶向下、自底向上或者两者混合运用建立简单或者复杂的几何模型，通常是经过各种布尔运算和操作建立所需几何实体，由于其优越性和实验结果与真实的一致性，是目前我们研究地下结构抗震运用较多的软件。

本文选用已建好的地铁五号线某车站结构作为研究对象，基于ANSYS大型有限元软件，重点分析该车站结构在罕遇地震及频遇地震作用效应，研究其抗震情况下位移及内力的大小及分布规律，为天津及全国其他软土地区地下结构的抗震设计提供相关依据。

2 建立模型

2.1 采用的计算模型、材料参数以及分析步骤

本文建立地铁车站三维模型，为了对比分析，在抗震分析中建立模型，模型的结构部分用土体填充，即：由土体和三个方向的弹簧单元组成的自由场模型。并施加重力荷载进行静力平衡计算，之后设定动力条件，输入地震波，实施相应的动力响应分析。本文中地震加速度采用三个方向输入的方式对所建模型进行瞬态抗震分析，输入的地震波为宁河天津波，“中国天津（1976）地震竖向记录”，天津波的记录时长为5s，时间间隔为0.01s，场地为第三类，记录信号为竖向加速度。在本次研究输入之前，对原始的记录数据做了部分调整。依据我国地震局烈度表，地面运动的水平峰值加速度a的平均值分别为0.125g，0.25g，0.5g分别为基本烈度7，8，9度相对应的数值，模型所在场地的基本烈度为7，则对于天津记录av/avmax=0.125g/2/73.14=1.5，所以天津波应该乘以1.5这个修正系数之后使用。

（1）本文研究所采用的土的模型为Drucker-prager本构模型。该模型的建立是在考虑静水压力的Drucker-prager屈服准则原则上建立的。

（2）在本次地铁车站结构采用线弹性模型。车站结构的材料为钢筋混凝土，弹性模量为28.5GPa，密度为2500Kg/m3，泊松比为0.2。

图1 整体有限元和车站结构模型

2.2 土体与结构的位移和应力包络图

在本文分别对三个模型进行抗震计算，一共计算了5s，每0.1s输出了一步长结果数据，所以最后总得到结果数据为几十组，通过了对这几十组结果数据中的x，y，z三个方向的位移值和三个方向的应力值进行了大量的数据统计，最终得到了Ⅰ、Ⅱ、Ⅲ三个模型中土体的x，y，z三个方向的位移包络图和x，y，z三个方向的应力包络图，Ⅰ、Ⅱ两个模型中结构的x，y，z三个方向的位移包络图。

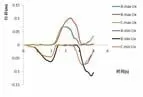
图2 土体x方向位移包络图

图3 土体y方向位移包络图

图4 土体z方向位移包络图

2.3 对比分析

（1）在X方向上正向位移，三个模型在0～2s正向最大位移变化一样的，而2s以后，模型A与模型C的变化时几乎可看成在一条线上，同时在第3s达到最大为0.069，然后逐渐变小直到第4s达到最小后才有发生逐渐变大的趋势；而模型B在第2～3.5s之间曲线成逐渐上升直到3.5s附近达到最大值0.1013（其值大于A、B模型在该方向的值），而后逐渐下降直到4.3s左右趋于零。

（2）在X负向上的位移，三个模型在0～4.3s的变化曲线是相似的，A、C模型变化可看成在一条线上，在0～2s曲线在负向位移绝对值呈逐渐增大的趋势直到第2s时达到第一个负向最大的绝对值即0.044，而B模型的负向绝对值为0.062大于其他两个模型的值，随后三个模型位移绝对值都逐渐减小直到2.5秒几乎为零，2.5～3.6s其变化曲线几乎成一条直线不变，3.6～4.3s三个模型的变化曲线呈现负向绝对值增大的趋势，在4.3秒附近A、C模型达到负向绝对值最大分别为0.074和0.072，随后又呈现负向绝对值逐渐减小的趋势，而对于B模型在4.3～4.9s继续呈现负向绝对值增大的趋势直到4.9秒时达到第二个负向绝对值最大即0.116（此值在负向上位移绝对值最大），而后又呈现负向绝对值逐渐减小的曲线

（3）在Y方向正向位移，三个模型位移包络线在0～2s时曲线几乎呈现一条直线，2～3.1s模型A,C的正向位移包络线呈现曲线逐渐上升，在3.1s分别达到最大值为0.106和0.113，3.1～4s模型A，C表现为逐步下降的曲线，在4s趋近于零，而后便没有多大的变化趋势。而模型B在2～3.5s是曲线显示为上升，直到在3.5s是位移达到最大0.131。3.5～4.2s曲线呈下降段直到接近于零，而后几乎没有多大的变化。

（4）在Y方向的负向位移，对于模型A、C在0～1.9s时曲线下降，但是位移绝对值呈增大阶段，直到在1.9s时达到第一个绝对值最大点，其值分别为0.064、0.070。1.9～2.4s曲线呈上升阶段，位移绝对值减小至零，2.4～3.7s几乎趋近零，3.7～4.7s曲线表现为下降阶段，位移绝对值增大，在4.7s时达到第二个最大点，位移绝对值分别为0.124、0.122。而后曲线有上升。对于模型B，0～2.1s曲线为下降段，位移绝对值增大，在2.1s时达到第一个绝对值最大点，即0.074，2.1～3.8s曲线上升，位移绝对值减小至零，3.8～4.9s曲线下降，位移绝对值达到第二个最大点，即0.150。

（5）在Z方向正向位移，三个模型的曲线变化复杂，但总体是呈上升的曲线，模型A在4.5s时达到最大值0.029，模型B在5s时达到最大值0.044，模型C在4.1s时达到最大值0.028。在负向上，三个模型的曲线同样是复杂多变的，总体上成下降阶段，而位移绝对值增大，A模型在4.5s达到绝对值最大为0.027，B在4.9s发生最大绝对位移值是0.039，C在4.1s呈现出绝对值最大为0.028

通过以上可知，地震载荷对土体产生的响应主要集中在 4～5s，可见此阶段是地震作用对土体的影响是最大的。在X、Y方向上正负位移值较大，故此在考虑地震作用影响时需要考虑这两个方向。

3 结论

对天津软土地基中地铁车站结构在不同模型下对地震波作用下的地震动力反应特点进行研究分析，总结出了一些地震动力响应特点如下：

（1）在地震作用下， X、Y方向受地震动影响的时间较长，而Z方向受其影响较短，所以在考虑地震动影响时可以首先考虑X、Y两个方向的影响。通过竖直边界不同取值建模对比分析，可得由于竖向土体选取的不同，受地震作用的影响也不同，主要是随着竖向土体的增加，地震作用对土体的地震响应逐渐增强，地结构地震动反应受周围土层的影响明显，

（2）通过测点分析，中柱、底部、侧边墙以及顶板中部的变形比较大，在抗震设计时应着重考虑。