面向5G需求的人群流量预测模型研究
胡铮,袁浩,朱新宁,倪万里
(北京邮电大学网络与交换技术国家重点实验室,北京 100876)
1 引言
随着移动网络技术的飞速发展,用户对网络的使用和需求无时无处不在,且数据业务量急剧增长,这一需求促进了5G技术的发展和5G网络的商业化进程。
通过对小型蜂窝网络的密集部署及移动边缘计算的应用,可以大大增强移动网络的带宽和服务质量。然而如何真正提高大量小基站的效率,充分发挥边缘计算的能力,是提升5G网络服务质量的关键问题之一。
由于用户数量和用户的业务需求是影响基站缓存部署、资源分配和能耗管理的重要因素,通过准确预测基站覆盖范围内的用户数量,对提高5G网络性能具有重要意义,尤其是针对某些基站所覆盖的特定的功能区域,如景区、办公区、住宅区等,由于不同区域具有其特定的业务需求模式,对区域内人群数量的预测,将有利于区域内网络资源的部署和分配。
首先,区域内人群流量预测有利于5G基站缓存部署及资源分配决策。靠近用户接入侧的5G小基站主要包括计算、存储和通信等资源,但由于硬件资源受限,小基站可能无法为所有用户提供足够的计算和缓存服务[1]。由于网络接入的用户流量将直接影响基站的缓存决策及计算和通信资源的分配方式,因此,基于不同基站下的人群流量差异,利用呼叫详单数据预测用户下一时刻的地理位置[2],再从全局角度研究5G网络中小基站和宏基站的最优缓存与资源分配策略,有望减小网络端到端时延,有效提高网络通信能力。
其次,人群流量预测有利于制订5G基站活跃/休眠切换方案。虽然为支持高速率移动通信服务和提供无缝覆盖的大量 5G基站功率较低,但总的 5G基础设施所消耗的能量将是显著的[3]。在维持移动用户服务质量的同时,关闭或休眠5G网络中未充分利用的小基站将是一种高效的节能方法。因此,从环保和经济效益的角度出发,准确的人群流量预测结果将为5G基站的活跃/休眠切换机制提供有力的参考依据和行动准则。
人群流量预测还有利于 5G基站密集部署规划。在5G时代,面对急剧增长的移动流量,小型蜂窝网络的部署可以提供巨大的网络容量,但 5G基础设施的大面积高密度部署将会带来高昂的建设成本和运营成本[4],因此,在保障用户流量需求的前提下,为最小化移动网络运营商的资本支出,需要通过对人群流量的预测来有效规划5G基站的部署位置与数量。
此外,区域人群流量预测本身还可以作为改进城市规划、实现特定区域如景区的监控和管理、进行交通流量管理、防范人群聚集的突发事件的重要依据。
随着位置信息获取技术的发展,大量标识用户时空位置的数据可以被用来实现区域的流量预测。基于移动网络的呼叫详单记录数据可以获取以基站位置标注的用户时空位置信息,因而可以作为表征全域覆盖范围内的区域人群流量的数据。基于该时空位置信息进行各种尺度的区域人群流量预测可以为5G基站的缓存部署及资源分配等应用提供重要的决策支撑。
基于用户位置信息的人群流量预测已有不少研究[5-16],文献[13-16]提出了基于深度时空学习的模型来实现对区域间依赖关系的自动提取,然而,人群移动使不同区域之间的流量存在一定的空间相关性,而流量在时间上存在连续性和周期性,且与短时流量密切相关,因此如何准确地对复杂的时空依赖关系进行建模是流量预测过程中的巨大挑战。其次,各种外部特征,如下雨、空气污染等的异常变化会给流量带来影响,其影响方式、程度和时间可能不同,因此如何将多维度的外部特征添加到预测模型中也是流量预测过程中需要解决的问题。此外,为了实现对短时间内流量的准确预测,需要利用临近时间的流量信息。为了降低对全局流量数据实时传输的需求,如何只利用局部实时数据,再结合较长期全局数据完成区域流量预测 也是流量预测面临的挑战。
基于上述分析,本文提出了一种基于时空残差网络和长短期记忆网络(LSTM, long short term memory)建模流量时空依赖关系,并融合各种外部影响因素,对短时流量信息仅依赖局部实时信息进行建模的深度时空网络流量预测模型。该模型在降低全局实时信息传输的同时,提高了预测精度,为后期基站资源部署和分配提供依据。
2 相关工作
2.1 5G网络部署与资源分配需求
5G具有基站大面积密集部署、微基站覆盖范围小等典型特征,这在给网络带来如提升数据速率、支持泛在接入等好处的同时,也给网络带来了新的挑战和要求,如小基站的部署选址问题、能效问题以及资源管理问题。为支持下一代移动服务的需求,5G网络的部署必然会涉及新基站设备的安装问题,因此,为最小化目标资本支出,5G网络规划本身就是一个复杂的问题,尤其是在人口密集的城市地区,这一问题更加凸显。Oughton等[4]提供了一个基于场景和移动流量增长的5G网络基础设施供需评估,而移动流量的直接生产者就是基站的接入用户,因此预测基站的人群流量密度能有效地降低运营商的部署成本。
为了满足热点场景下大规模聚合数据速率的需求,密集部署的5G基站具有一定的冗余,因此,在低功耗基站较多的情况下,需要关闭/休眠大量空闲基站来实现节能,但关闭/休眠基站会增加附近多个基站的流量负载,即不同基站之间的开关状态和用户服务质量存在高度依赖关系。Feng等[3]研究了5G网络中开关基站的有效方法与所面临的挑战,如根据用户的流量类型调整基站的运行模式,进而提高系统性能。
近年来,在移动设备上部署计算密集型的应用日益增多,超低时延已成为实现高用户体验的重要需求保障。为解决这个问题,能有效节省网络带宽和降低端到端时延的最优缓存与网络资源分配策略受到了广泛关注。Chen等[1]提出了一种高效收集全局可用资源信息的移动网络架构,并设计了一个由小基站和宏基站组成的最优缓存策略以最小化网络时延。不同的人群流量将会带来文件流行度与计算任务卸载的差异,在网络边缘考虑人群流量密度可以为进一步提高缓存命中率与制定卸载决策提供有效依据。
2.2 人群流量预测
近年来,城市范围的人群流量预测受到了研究人员的广泛关注,无论是传统的时间序列模型,还是近来广为流行的深度学习框架,都在人群流量预测领域有所建树。
基于时间序列模型进行流量预测,主要考虑的是流量数据的时间依赖关系,比如Kumar等[5]提出了一种基于卡尔曼滤波技术的预测方案,可以仅使用较少的历史数据来实现流量预测;而Li等[6]则提出了一种改进的自回归移动平均模型(ARIMA,autoregressive integrated moving average)来预测热点地区的流量变化;类似地,Matias等[7]同样提出了一种出租车乘客短期空间分布预测方案,将数据聚合成直方图时间序列并结合3种时间序列预测技术进行预测。近年来,在时间序列预测模型的基础上,研究人员也开始进一步探究空间依赖关系以及相关外部影响特征的建模,比如Tong等[8]提出了一种具有2亿多个特征维度的线性回归模型,结合了时间、空间、外部特征等多个维度的大量特征,实现了出租车需求预测;Wu等[9]结合了兴趣点(POI,point of interest)、天气、地理标记等多域数据,从不同视角对出租车需求进行了分析与预测。然而,即便充分结合了各种附加因素,预测结果仍难很好地反映复杂的非线性时空相关性[10]。
随着深度学习技术的不断发展和完善,并考虑到流量预测的时空建模的复杂性,利用深度学习的模型进行流量预测受到了更多研究人员的青睐。Liu等[11]提出了一种新的端到端深度学习体系结构,基于 Conv-LSTM(convolutional long short-term memory)模块提取流量的时空特征,从而实现了良好的流量预测性能;Polson等[12]针对由异常特征导致的急剧的异常流量变化问题,提出了一种深度学习的框架,证明深度学习架构可以捕捉这些非线性时空效应,此外,Zhang等[13-14]充分考虑不同历史时间层的影响分别建模,并结合天气、元数据等外部特征,搭建了复杂的深度学习网络 DeepST和ST-ResNet(spatio-temporal residual network),得到了明显的性能优化和提升;最近,Huang等[15]提出了一种新的犯罪预测框架——DeepCrime,该框架可以揭示犯罪数目的动态的变化模式,探索其随时间的演变模式以及与其他信息的动态关联,在犯罪预测上取得突出的效果。
上述研究工作为区域人群流量预测提供了基础,本文将主要针对复杂的时空依赖关系、外部因素的影响以及为5G网络资源分配提供决策依据时所需的短时流量预测等问题进行人群流量预测的建模。
3 区域人群流量预测模型
3.1 系统模型
考虑到同一类功能区如景区、住宅、商业区等具有相似的人群流量模式和业务需求模式,本文在进行整个城市范围的流量预测时,首先对城市进行基于兴趣点(POI,point of interest)分布的分区。目前的城市分区方案[10,12-14]更多考虑的是城市的规模、范围等,但缺少对分区过程的约束,可能导致不同功能区之间的混叠。以景区为例,景区覆盖范围内一般包括多个基站,如果隶属于不同景区的基站被划分至同一网格,由于基于移动网呼叫详单数据的用户位置信息是由其连接的基站所定位,这种混叠自然会影响景区间空间依赖关系的建模与景区流量的计算和预测。因此,在本文中,为了避免这种混叠的出现并尽可能减少后续预测的复杂度,在分区过程中加入以下约束:1)避免将不同功能区的基站映射到同一个网格;2)尽可能减少城市分区的数目。基于此,可以将城市划分为I×J的网格图。而要预测的区域(功能区)可以视为相邻网格的聚合。如图1所示,该模型可运行在区域中的宏基站或具有相应计算和存储资源的基站上。
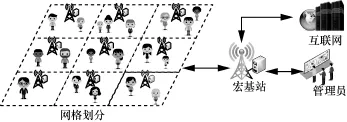
图1 面向5G需求的基站接入人群流量预测系统模型
本文涉及的符号及其含义如表1所示。

表1 符号标记及其含义
定义1 流量。在第t个时间段,网格(i, j)内的流量定义如式(1)所示。
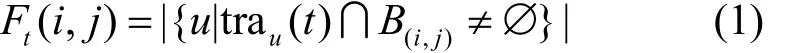
其中,|⋅|表示集合内元素的数目,trau(t)表示用户 u在时间段 t内通信的基站集合。B(i,j)表示区域(i, j)内的基站集合。在第t个时间段,所有I×J个区域的流量可以表示为矩阵 Ft∈RI×J,也可用时间段 t的流量图表示。类似地,在第t个时间段,第i个区域的流量可以定义为其中,Mi表示第i个区域内的基站集合。在第t个时间段,所有p个区域的流量可以表示为区域流量向量。
3.2 基于深度时空网络的人群流量预测模型
基于区域流量预测问题,本文提出的流量预测模型的整体框架如图2所示,主要包括3个模块,分别是外部特征模块、时空模块和图嵌入模块,图中分别用虚线框标识的a、b、c指出这3个模块。该模型从3个不同的角度对区域流量预测问题进行建模。
外部特征模块提取预测所需的所有历史时段的各类外部特征,包括天气、空气质量、节假日、时间等元数据特征,并将这些外部特征按照时间顺序拼接为矩阵的形式,送入全连接层1中,进行特征的提取与优化。
时空模块将时间轴划分为3个层次,即临近层、周期层和趋势层,分别表示临近时间、较近和较远的历史时间,在不同时间层内,按照一定周期取相应时间长度的历史流量数据作为输入。由于临近层输入为短时间内的流量数据,为降低实时数据传输需求,本模型中仅需要局部流量数据,即通过当前预测区域的宏基站提供的区域内短时的流量向量。而周期层和趋势层的输入为长时间的流量,这部分数据不需要实时的数据传送,故取对应时段的全局流量图。
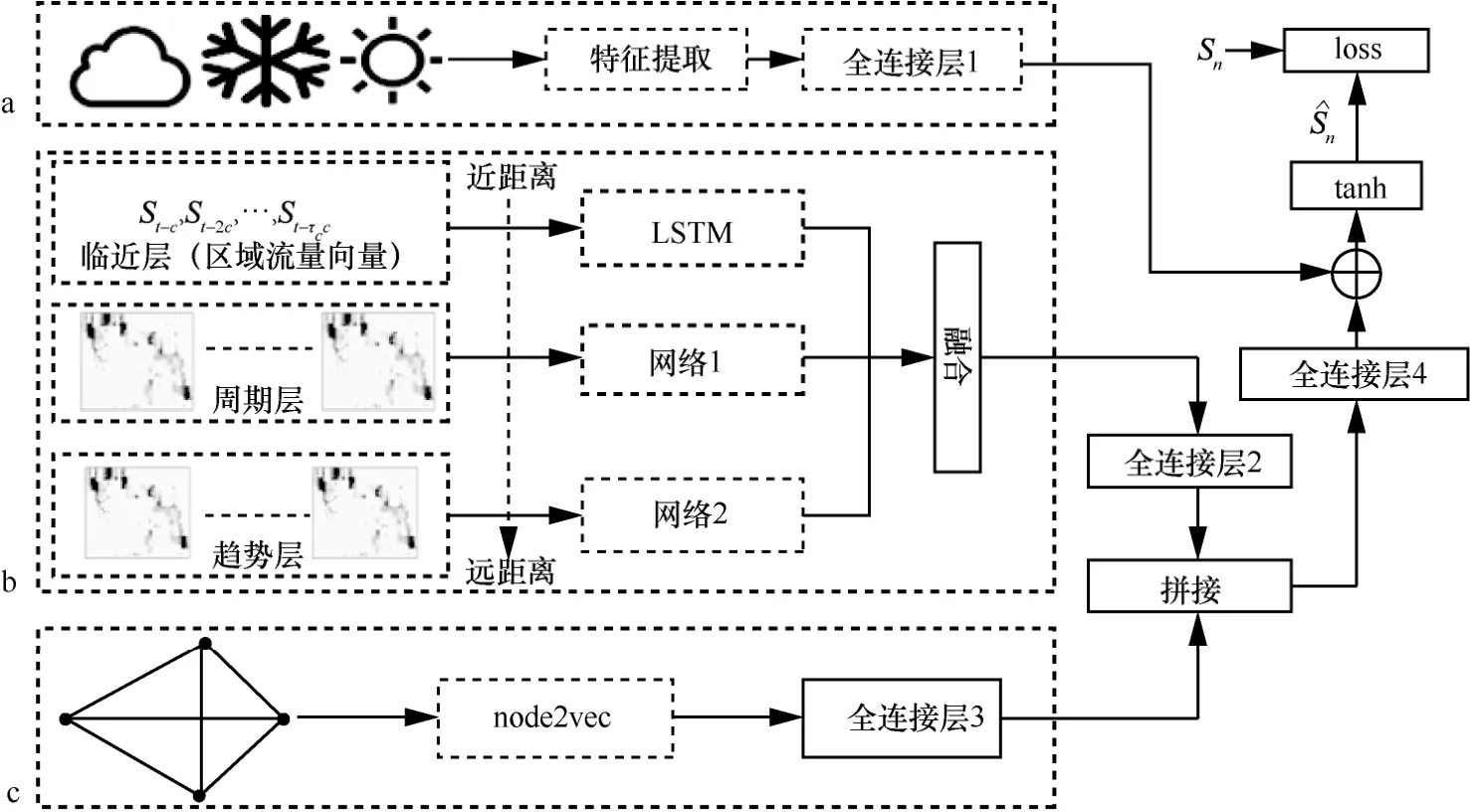
图2 基于深度时空网络的区域流量预测模型
3个层次的流量输入分别送入相互独立的3组神经网络,对不同时间层的影响进行建模,其中,针对临近时间层,利用LSTM模块捕捉其时间上的相关性;周期层与趋势层则构建残差神经网络来对时空依赖关系协同建模。最后,针对图嵌入模块,为要预测的区域之间构建区域距离图,并利用node2vec将其抽取为向量,通过全连接层3进行特征提取,作为另一视角的流量预测结果。
在预测输出部分,将3个时间层的输出进行基于参数矩阵的融合,并通过全连接层2优化预测结果,作为时空模块的预测输出SST。然后,将其与图嵌入模块的输出进行拼接,并将拼接的结果送入全连接层 4,进行特征的提取与优化。最后,将输出结果与外部特征模块的输出叠加,并通过tanh函数将结果映射到[-1,1],以便在训练过程中得到更快的收敛速度。
3.2.1 外部特征模块
外部特征(如天气、空气质量、节假日信息等)对相关区域的流量可能产生巨大的影响,例如,在下雨天或空气质量差的情况下,前往景区的人数一般都会明显下降,如何衡量这种由于外部特征所带来的流量波动,如何准确地对多维外部影响特征建模,是进行区域流量预测时需要重点考虑的问题。本文针对时空模块预测中涉及的所有历史时段,对每个时段t分别提取一组特征向量Et,具体如表 2所示。将不同时段的特征向量拼接为矩阵的形式,送入全连接层1进行特征提取,得到p维的区域预测向量,即为外部特征模块的预测输出,记为SEX。

表2 外部特征描述
3.2.2 时空模块
时空模块主要包括3个相互独立的处理单元以及融合输出部分。在3个时间层中,以一定的周期c, pr, tr选取一定长度(lc,lpr,ltr)的历史流量数据作为输入,分别表示临近时间、较近和较远的历史时间,其中,临近层的输入为对应时间区域流量向量,而周期层以及趋势层都是以多组流量图作为输入。
对于临近层,可以通过宏基站获取实时的预测区域的流量数据。然而仅依据局部区域的流量数据难以对流量的空间依赖关系准确建模,因此临近层采用如图3所示结构的时间序列模型LSTM建模,充分考虑临近时间段内区域流量数据的时间依赖特性。
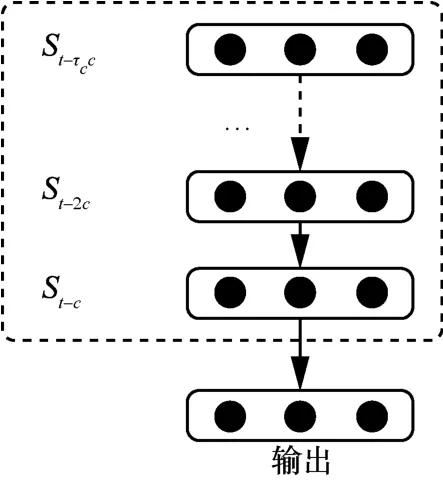
图3 LSTM模块的基本结构
LSTM 模块共包括lc个时间单元,每个单元的输入为对应该时段的区域流量向量,该模块的最终输出即为下一时段的p维区域流量向量,记为Xc。
而在周期层和趋势层中,利用较远的历史时间的全局流量信息(即整个城市范围的流量数据)挖掘更为丰富的时空依赖关系。对每个时间层,将多个历史时段的流量图组合为类似视频形式的多通道输入信息,并通过结构完全一致的2个并行的残差网络1和残差网络2进行后续的时空依赖关系的建模,其结构如图4(a)所示。
多通道的输入信息通过卷积层1进行初步的特征提取。输出的特征映射被送入2个连续的残差单元(残差单元1和残差单元2),残差的基本结构如图4(b)所示,即用卷积层来拟合的不是直接的映射关系,而是残差映射。相比于卷积层的堆叠,残差学习的优势在于随着网络深度的加深,模型至少可以保证性能不会变差,这样就通过残差单元的堆叠实现了对远距离的空间依赖关系的建模。
最后,残差单元2的输出被送至全连接层,将其映射到p维的输出向量,从而得到该时间层的预测输出。周期层和趋势层的输出分别记为Xpr和Xtr。
通过LSTM模块、残差网络1和残差网络2,可以实现从3个不同的时间尺度上挖掘丰富的时空信息。但不同时间层的影响程度很难直观给出判断,因此参考论文文献[16],为了将 3个时间层的输出以更为恰当的权重进行融合,本文采用基于参数矩阵的融合方式,如式(3)所示。
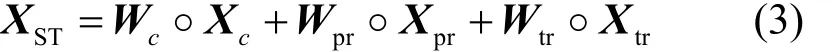
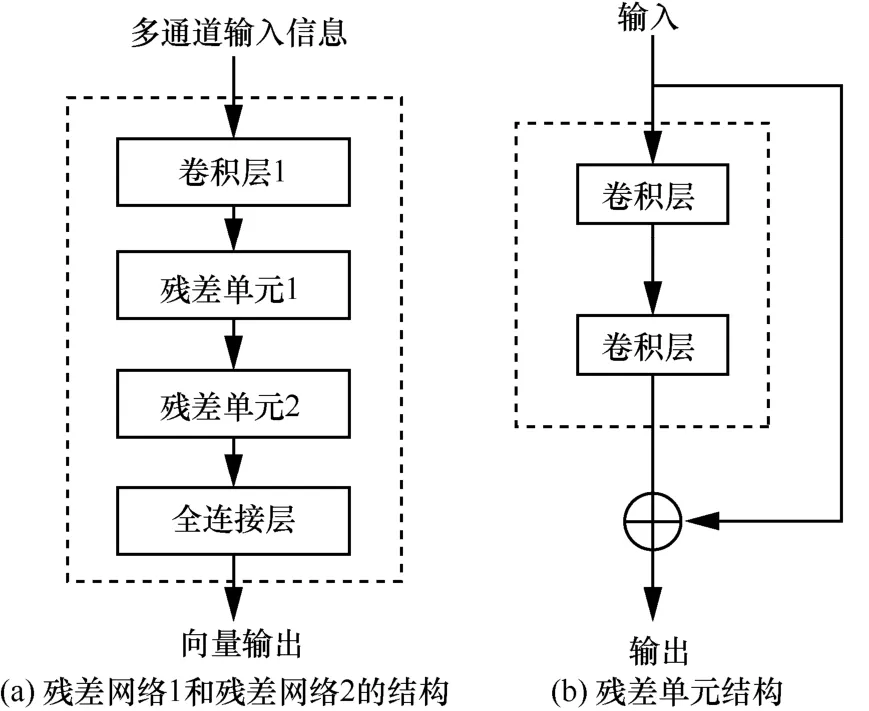
图4 残差网络1和残差网络2的结构
其中,◦表示哈达玛积,即2个矩阵的元素对应位置相乘,最终可以得到同维度的输出矩阵。Xc、Xpr、Xtr分别表示3个时间层的输出,而Xc、Wpr、Wtr则表示不同时间层的权重矩阵,即在网络训练中要学习的参数,来调整不同部分对结果预测的重要程度。
得到融合向量后,经由全连接层2进一步优化预测结果,最终得到时空模块的预测向量输出SST,如式(4)所示。
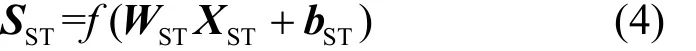
其中,WST和bST分别表示模型需要学习的参数,f(⋅)表示该全连接层的激活函数,在本文中,除特殊说明外,激活函数均选用relu函数。
3.2.3 图嵌入模块
除了历史流量数据的影响,人群移动模式信息也可能反映出区域之间的某种内在相关性,例如人们更倾向于在相距较近的区域之间转移,尤其是在一段较短的时间内,这种普遍的人群移动规律就会使得近距离的区域之间会有较强的流量相关性。捕捉这种人类移动模式视角上的空间依赖关系,可以从另一个角度对区域间的相关性进行建模,从而为流量预测提供有价值的信息。因此,本文提出的模型添加了区域距离图的嵌入模块,从而更为直观地构建区域之间与空间距离相关的流量相关性。
具体来说,即为要预测的p个区域之间构建转移距离图G=(V,E,D),其中,V表示待预测的区域,E∈(V×V)表示边的集合,wij表示边的权重,即区域i和区域j之间的距离量度。考虑到距离越近的区域之间可能有更大的流量相关性,以负指数距离来表示边的权重,如式(5)所示,以保证更大的边权重对应于更强的流量相关性。

其中,λ表示距离的衰减系数,本文中取λ=-0.1;dis(i,j)表示区域i和区域j之间的地理距离(单位为km),通过计算两区域中心点之间的距离而得到。
为了将图中的信息与深度神经网络协同训练,本文考虑了一种图嵌入方案,即在不破坏图结构的前提下,以向量的形式提取出每个节点的信息。本文选择 node2vec模型[17],通过一个二阶的随机游走来平衡广度优先搜索和深度优先搜索,从而更好地保留图的结构和连通性。通过node2vec得到不同节点的嵌入向量输入全连接层3进行特征提取与优化,输出一个包含p列的矩阵,记为SSE,作为图嵌入模块的输出。
3.2.4 模型训练与预测输出
为了将外部特征模块、时空模块以及图嵌入模块进行协同训练,首先将得到的p维行向量SST和包含p列的矩阵SSE进行按行拼接,即

然后将XET送入全连接层4,如式(7)所示。
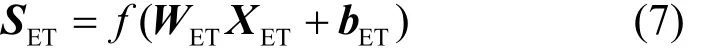
其中,WET和bET表示需要学习的参数,f(⋅)表示全连接层4的激活函数。
最后将SET与外部特征模块的输出SEX叠加后,送至tanh层,如式(8)所示。
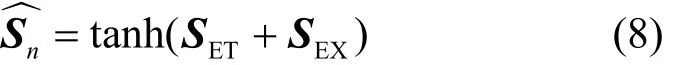
其中,tanh函数用于将预测结果映射至[-1,1]。最终得到的是维度为p的向量,对应下一时段p个区域的流量预测结果。完整的算法流程如算法1所示。
算法1模型训练过程
输入临近层、周期层、趋势层的周期c、pr、tr,
临近层、周期层、趋势层的序列长度lc、lpr、ltr
景区距离图G
历史流量图{Ft|t=0,1,2,…,n-1}
历史外部特征向量{Et|t=0,1,2,…,n-1}
景区历史流量向量{St|t=0,1,2,…,n-1}
输出训练得到的景区流量预测模型
1) begin
2) D=(/)
3) 在图G 上,基于node2vec 计算得到矩阵ZSE
4) for all available t (1≤t≤n-1) do
5) ZE=[(Et-c,… ,Et-lec),(Et-pr,… ,Et-lprpr),(Et-tr,… ,Et-ltrtr)]
6) ZC=[St-c,… ,St-lec,St-pr,… ,St-lprprSt-tr,… ,St-ltrtr]
7) ZPR=[Ft-pr,Ft-2pr,… ,Ft-lprpr]
8) ZTR=[Ft-tr,Ft-2tr,… ,Ft-ltrtr]
9) ((ZC,ZPR,ZTR,ZE,ZSE),St)→D
10) end
11)//模型训练
12)初始化模型中的所有参数θ
13)repeat
14)从D中随机选取batchDb
15)基于Db,通过最小化损失函数来找到最优化的θ
16)until 满足停止条件
17)end
模型训练首先遍历所有可能的时间段,生成基于每个时间段的训练样本(即步骤2)~步骤10)),然后对训练集提取batch,并运用反向传播算法优化模型参数(即步骤12)~步骤16))。其中,损失函数定义如式(9)所示。

其中,θ表示所有需要训练参数的集合。模型训练的过程即最小化L的过程。
4 实验结果与性能分析
4.1 实验设计
本文应用某旅游城市的移动网络运营商提供的一个月的呼叫详单数据来验证人群流量预测模型的效果和性能。考虑到景区作为该城市重要的网络服务区域,景区人群流量预测的准确性将会影响到部署在景区的基站的服务质量,因此本文选择景区人群流量预测作为实验对象。数据包括超过百万个匿名用户的上亿条呼叫详单记录,每条数据包含匿名的用户ID、时间戳、接入基站编号及经纬度信息。为了应对大规模的数据处理,采用了 Apache Spark集群计算框架。此外,还从气象网站上爬取了该数据对应的时间段的天气、空气质量等数据,用于外部特征的建模。
首先对呼叫详单数据进行预处理,剔除无效数据、异常和漂移数据,并处理了基站间反复切换的乒乓效应[18-19]。此外,考虑到在输出端利用tanh函数作为最终的激活函数,为了将输出数据与标签数据匹配,在输入端基于最小最大归一化对流量数据进行了归一化处理,将输入数据均映射到[-1, 1],用于神经网络的训练。在后续的模型评估中,再将预测值重新调整回正常值,与真实值进行对比,从而得到准确的预测误差。
模型基于TensorFlow实现。实验共选取了25个景区作为预测区域(功能区),并将全市划分为85×110的网格图。首先对临近层、周期层和趋势层的周期分别选定为30 min、1 d和1 w,而每个时间层中的时间序列长度,分别选择lc=6、lpr=2、ltr=1。实验预测的是未来30 min各景区的人群流量。
在神经网络参数的设置方面,临近层的LSTM单元选择6个时间单元,分别对应过去的6个临近时间段周期层和趋势层共享同样的网络结构,其中,卷积层1选择5×5大小的32个卷积核,残差单元中的所有卷积层均选择3×3大小的32个卷积核。最终3个时间层均输出25维的向量,经过融合和全连接层的特征优化,时空模块的最终输出同样为25维行向量。
在图嵌入模块,经过node2vec,每个景区节点生成10维向量,将其拼接为10×25的矩阵,经过全连接层处理得到4×25的输出矩阵。
在外部特征模块,每个时间层构造一组如表 2所示的 10维外部特征向量,将所有时空模块涉及的历史时段的外部特征向量送入全连接层,输出为25维的景区预测向量。具体训练过程中,选取的batch数目为64,选择数据集80%的样本作为训练集,剩余的20%作为测试集。实验中应用早停法来选择最优的模型参数。
本文选用均方根误差(RMSE, root mean sguard error)作为模型的评价指标,其定义如式(10)所示。
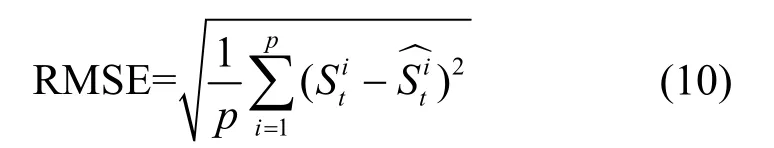
4.2 对比算法
为了验证模型的预测效果,将本文提出的预测模型与以下8组模型进行了对比,其中涉及的实验数据、损失函数、评价指标等都与本文模型相同。
HA模型即直接平均算法,根据历史同一时段的流量数据进行预测。比如要预测周二上午10:00的流量数据,即选择历史数据中所有的周二上午10:00的流量平均值作为预测值。
ARIMA模型简单的线性模型,根据周期性关系,建立预测数据与历史数据之间的线性关系,可以在一定程度上进行拟合。
VAR模型是一种高级的时空预测模型,可以捕捉不同输入流量之间的相关性,由于参数量的庞大,计算复杂度非常高。
卡尔曼滤波模型[5]借鉴卡尔曼滤波的基本思想且只需要短时间的历史数据,利用历史数据生成连续时间之间的流量转移比,并应用到要预测的时间上。
ST-image模型[20]一个基于深度学习的短时交通速度预测模型。该模型以图片的2个维度分别表示空间和时间,以时空图片作为输入。
LSTM模型一种特殊的RNN模型,能够学习长距离的时间依赖关系。这里在2组不同的参数上进行了实验,即LSTM-12和LSTM-48。
DeepST模型[14]一个基于DNN的时空流量数据预测模型,对时间、空间和外部特征进行了协同建模,在城市范围内的流量预测上取得了较好的性能。
ST-ResNet模型[13]相比于DeepST,在网络中应用了残差学习的思想,取得了相比于DeepST更好的预测效果。
与此同时,本文还研究了本文模型的各类变种的性能,具体如下。
本文模型变种1将临近层的LSTM单元修改为一个全连接层,其余结构不变。
本文模型变种2将临近层的输入调整为多时间段的具有全局信息的流量图,并将LSTM单元修改为同残差网络1和残差网络2同样的结构,其余不变。
本文模型变种 3将景区距离图嵌入模块移除,最终的流量预测结果仅取决于时空模块以及外部特征模块的预测结果,来探究景区距离图嵌入模块的作用。
4.3 结果对比与分析
本节将通过与多组对比算法以及模型自身变种的性能比较,评估了本文提出的模型性能。考虑到景区在工作日和周末可能有明显的流量差异,实验分为工作日和周末两部分进行,对比结果如表3所示。
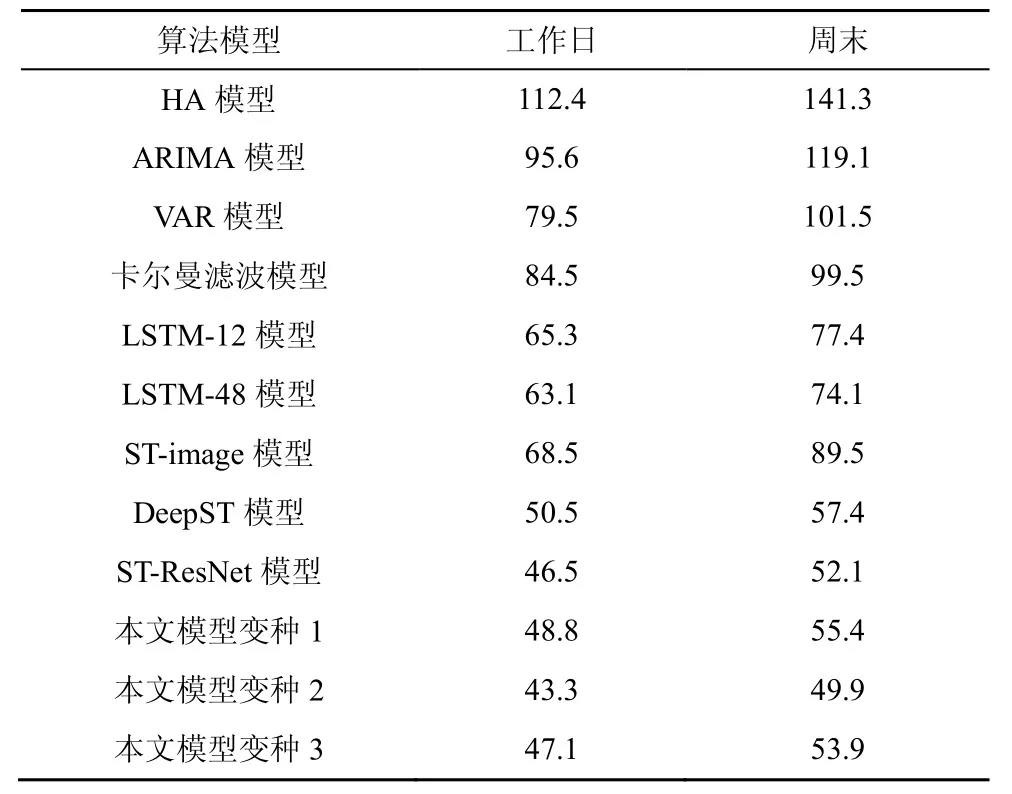
表3 不同模型的预测误差(RMSE)的对比
本文将对比模型划分为3类,即时间序列模型、时空深度学习模型、本文提出的模型及其变种。针对工作日的模式,从结果可以看出,本文提出的模型优于全部的时间序列预测模型,即使是相比于基于深度学习的LSTM模型,本文的模型也取得了28%~30%的性能提升,这充分说明了空间依赖关系在人群流量预测问题上的重要性;而相比于时空深度学习的对比模型,本文的模型依旧表现最佳,相比于 ST-image模型有接近34%的性能提升,即便是相比于利用所有时段的全局流量信息的DeepST模型和ST-ResNet模型,本文的模型也能得到 1%~10%的预测效果的提升,这说明在临近层通过LSTM建模并结合景区距离图的信息,可以实现对临近时间全局信息的近似建模。也就是说,在不需要全局实时流量信息的情况下,依然可以取得良好的预测性能。
通过对本文模型得3个变种的分析可以看出,变种1性能相比于本文的模型下降约6%,证明了LSTM模型在临近时间建模上的明显优势,因为其可以对较长间隔的时间依赖进行建模;变种2中将全局流量图应用于临近时间时,可以获得4.6%的性能提升,证明了全局流量信息的价值;变种3则由于景区距离图的移除,性能有所下降,说明景区距离图的嵌入为景区流量预测提供了一定的支持。图5直观给出了各模型的性能排序结果。
针对周末的模式,从结果可以看出,其在预测误差上都明显大于工作日模式。对于结合了外部特征的模型,如本文模型、ST-ResNet模型、DeepST模型等,相比于工作日模式的误差增加幅度较小,且在性能上明显优于其他模型,证明了外部特征在流量预测问题中的巨大作用。而本文模型依旧在所有对比模型的表现最优。图6直观给出了各模型在周末模式的性能对比结果。
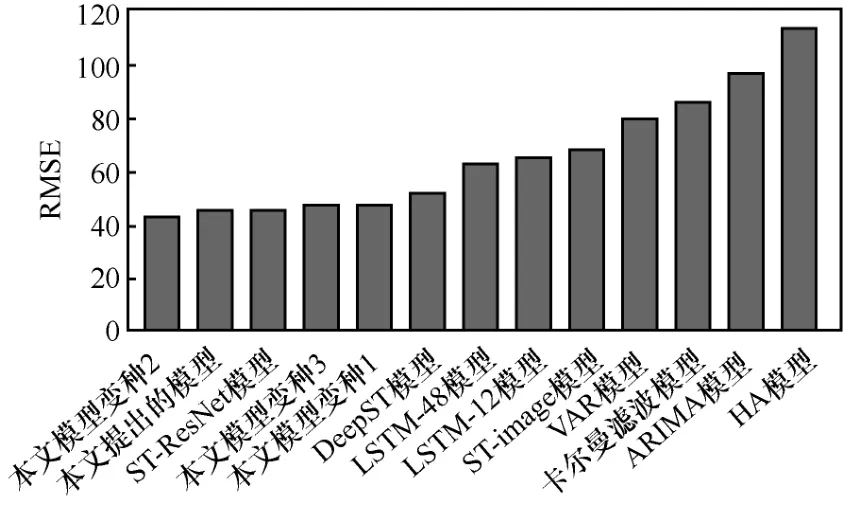
图5 各模型测试结果对比(工作日)

图6 各模型测试结果对比(周末)
4.4 参数分析
本文提出的模型在时间建模中选择了 3组参数,分别是lc、lpr、ltr,表示不同时间层的取样长度,即利用过去多长的时间来对未来的景区流量进行预测。下面分别调整3组参数的大小,来测试不同参数取值下的测试误差RMSE。
首先测试lc的取值,将另外 2组参数固定为lpr=2、ltr=2,将lc的取值从2变化至8,RMSE的变化如图7所示。从图7可以看出,当lc=6时,预测性能最好,这说明预测的性能并不是随着历史数据的增多而不断变好的,当增加到一定程度时,预测性能可能会变差。
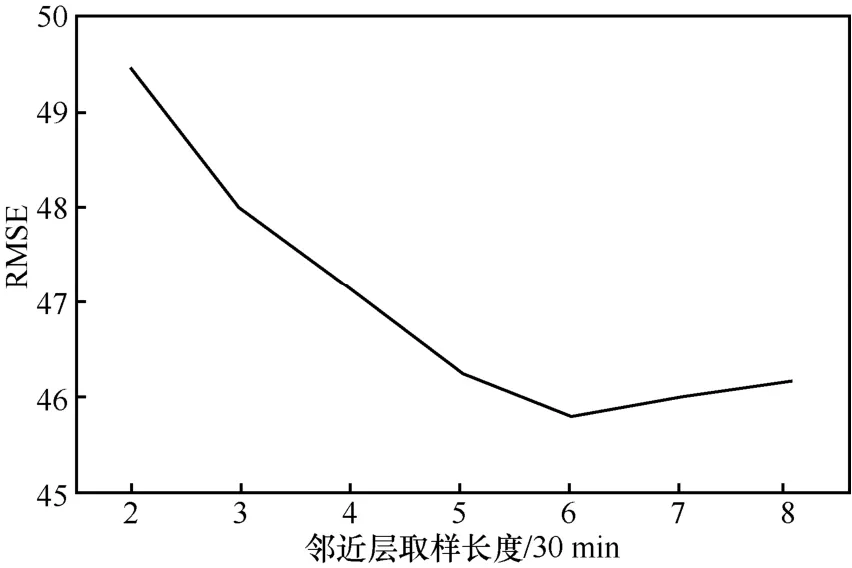
图7 临近参数lc的取值测试
然后测试lpr的取值,将另外 2组参数固定为lc=6,ltr=2,将lpr的取值从0变化至4,其中0表示不添加周期。RMSE变化如图8所示。从图8可以看出,当不添加周期层时,预测误差明显增大,证明了周期层数据的作用。而当lpr=2时,预测性能最优。
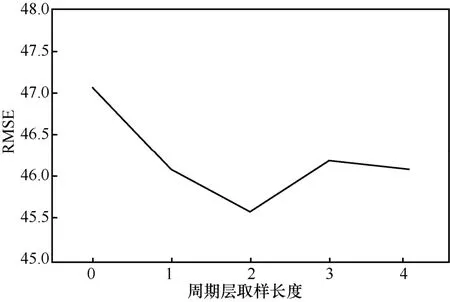
图8 周期参数lpr的取值测试
最后,测试ltr的取值,将另外2组参数固定为lc=6、lpr=2,将ltr的取值从0变化至3,其中0表示不添加趋势层。RMSE的变化如图9所示。同样地,不添加趋势层时网络性能最差,说明较长间隔的历史时间也会给流量预测提供有价值的信息。对于参数ltr,当其取值为1时,预测误差最小。综合以上分析,选择3组的取值为lc=6、lpr=2、ltr=2。
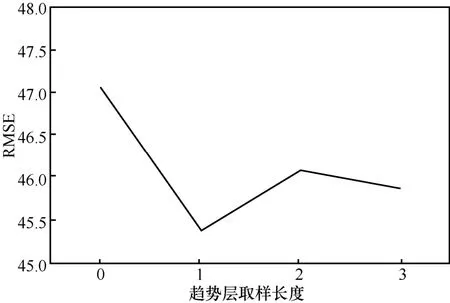
图9 趋势参数ltr的取值测试
5 结束语
5G网络服务质量的保证,要基于其资源分配、缓存策略、能耗管理等诸多策略执行的优劣。而准确预测各区域用户数量对提高 5G网络这方面的性能具有重要意义。本文提出了一种移动网络覆盖范围内的区域人群流量预测的深度时空网络模型,通过融合各种外部特征信息,对不同尺度的时空依赖关系建模,对短时流量信息仅依赖于区域内局部实时信息,在降低对实时信息传送需求的同时,也保障了预测的准确性。通过基于呼叫详单数据进行的景区人群流量预测,验证了本文提出的模型对工作日和周末的流量预测精度都比已有流量预测模型有显著提升。在下一步工作中,可以将基站的人群流量预测应用于 5G网络资源配置与流量分析的应用中。同时,随着5G网络基站大规模部署的开展,基于本文研究工作进行基站活跃/休眠的集群策略研究也将具有重要意义。

