On the Role of Differentiation Parameter in a Bound State Solution of the Klein-Gordon Equation∗
B.C.Lütfüolu
Department of Physics, Faculty of Science, Akdeniz University, Dumlupinar Bulvari, 07058 Antalya, Turkey
Department of Physics, Faculty of Science, University of Hradec Kr´alov´e, Rokitansk´eho 62, 500 03 Hradec Kr´alov´e,Czechia
(Received August 18, 2018; revised manuscript received November 26, 2018)
Abstract Recently, the bound state solutions of a confined Klein-Gordon particle under the mixed scalar-vector generalized symmetric Woods-Saxon potential in one spatial dimension have been investigated.The obtained results reveal that in the spin symmetric limit discrete spectrum exists, while in the pseudo-spin symmetric limit it does not.In this manuscript, new insights and information are given by employing an analogy of the variational principle.The role of the difference of the magnitudes of the vector and scalar potential energies, namely the differentiation parameter,on the energy spectrum is examined.It is observed that the differentiation parameter determines the measure of the energy spectrum density by modifying the confined particle’s mass-energy in addition to narrowing the spectrum interval length.
Key words: Klein-Gordon equation, generalized symmetric Woods-Saxon potential, bound state spectrum,spin symmetry limit, analytic solutions
1 Introduction
In nuclear physics, the spin symmetry (SS)and pseudopsin symmetry(PSS)concepts,originally postulated by Smithet al.[1]and Bellet al.,[2]were widely used to explain the nuclear structure dynamical phenomena.[3−7]The basics of these symmetries were explored comprehensively and the conclusion was that they depended on the existence of vector,Vv,and scalar,Vs,potential energies.[8−10]In 1997, Ginocchio revealed that PSS and SS occur with an attractive scalar and a repulsive vector potential energies that satisfyVv+gVs=ε−,Vv −gVs=ε+conditions,respectively.[10]
The Dirac equation (DE)was investigated by using various potential energies in the SS and PSS limits.For instance in the SS limit, Weiet al.obtained an approximate analytic bound state solution of the DE by employing the Manning-Rosen potential,[11]the deformed generalized Pöschl-Teller potential[12]energies.Furthermore,in the same limit,they proposed a novel algebraic method to obtain the bound state solution of the DE with the second Pöschl-Teller potential energy.[13]In their other work,they examined the symmetrical well potential energy solutions in the DE within the exact SS limit.[14]They contributed the field with important papers in the PSS limit too.For instance, they discussed an algebraic approach in the DE for the modified Pöschl-Teller potential energy.[15]Moreover, they applied the Pekeris-type approximation to the pseudo-centrifugal term and investigated the bound state solutions in the DE for Manning-Rosen potential[16]and modified Rosen-Morse potential[17]energies.
Another relativistic equation, Klein-Gordon equation(KGE),also has been the subject of many scientific investigations in the SS and PSS limits.Maet al.studied theD-dimensional KGE with a Coulomb potential in addition to a scalar potential.[18]Donget al.obtained the exact bound state solution of the KGE with a ring-shaped potential in the SS limit.[19]Hassanabadiet al.studied the radial KGE for an Eckart and modified Hylleraas potential energy inDdimensions by using supersymmetric quantum mechanics technique.[20]In another paper, Hassanabadiet al.sought solutions of bound and scattering states on the Pösch-Teller potential energy in the KGE in the SS limit.[21]In the same year, Hassanabadiet al.examined the KGE with vector and scalar Woods-Saxon potential(WSP)energy and presented the scattering case solutions in terms of hypergeometric functions.[22]Only a while ago, Sargolzaeiporet al.extended the KGE in the presence of an Aharonov-Bohm magnetic field for the Cornell potential.Then, they introduced superstatistics in deformed formalism and derived the effective Boltzmann factor with modified Dirac delta distribution.[23]
Recently, we examined the scattering and bound state solutions of the KGE under the generalized symmetric Woods-Saxon potential (GSWSP)energy in the SS and PSS limits.[24−25]We observed that in the scattering case,the solutions existed in the SS and PSS limits.[24]In the bound state case, unlike the scattering case, bound state solutions existed only in the SS limit.[25]
GSWSP energy is the generalization of the wellknown WSP energy[26]by introducing surface interaction terms,[27]and has been investigated in many research articles.[28−46]In one spatial dimension, it is given in the form of
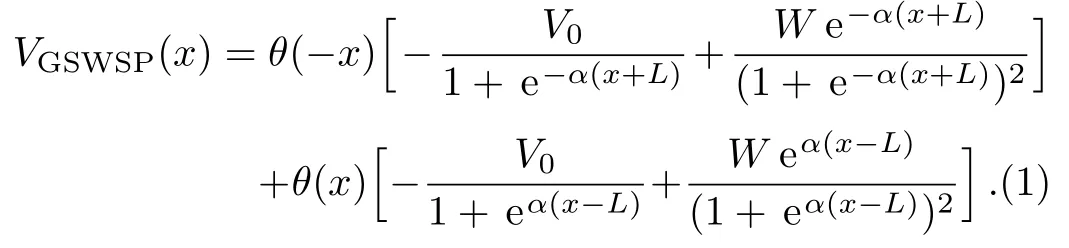
Here,θ(±x)denotes the Heaviside step function.GSWSP energy possesses four parameters.Among them,V0controls the potential well depth,Ladjusts the effective well length andαdetermines the well’s slope.These three parameters have positive values in this paper to allow an investigation of the bound state solutions in a potential well.The fourth parameter,Wis the additional one to the parameters of the WSP and it determines the surface effects type and magnitude.Since the GSWSP energy was mathematically derived with the first spatial derivative of the WSP,theWparameter is linearly proportional to the other three parameters.The proportionality constant can be either negative or positive, and it is used to determine whether the surface effect is attractiveW <0,or repulsiveW >0.[27]
On the other hand,in classical mechanics,an instantaneous configuration of a system is described byNgeneralized coordinates.A set of the generalized coordinates that is composed of both the coordinates and their respective momenta is represented with a point in the phase space.The development of the system over time is expressed by the motion of the point in the configuration space.Consequently, the motion of the system between any two distinct times is defined by the trajectory (N-dimensional curve)in the configuration space.Note that,the resultant curve in the configuration space is called “the configuration space trajectory” and it should not be interpreted as the real trajectory of any particle.
In general, in a configuration space there is an infinite number of configuration space trajectories between two points.All physical systems determine their configuration space trajectory by the Hamilton’s principle.Hamilton’s principle states that the true evaluation of a system between the initial and final points in the configuration space is described by that configuration space trajectory(among infinite number of all possible configuration space trajectories),along which the action functional has a stationary point.
The Hamilton’s principle, sometimes called the variational principle, has a wide usage in physics, not only in classical mechanics but also, in the theory of relativity,statistical mechanics, quantum field theory, etc.[47−48]
In this paper,our main motivation is to investigate the role of theε+parameter, hereby we call it the differentiation parameter, on the energy spectrum via an analogy of the variational principle.We assume the differentiation parameter is the only generalized coordinate that determines the bound state energy spectrum.We assign different values to the differentiation parameter and we calculate their corresponding spectra.In the analogy of the Hamilton’s principle, we assume those spectra are different configuration space trajectories.Then, we investigate the role of the differential parameter on the spectra.
Note that,it is a very well known fact that the differentiation parameter is equal to zero in finite range potential wells.[49]This value corresponds to configurational space trajectory in the language of the variational approach.
We construct the paper as follows.In Sec.2, we start with the KGE in the SS limit and closely followed the paper.[24]We obtain the most general bound state solution in the presence of the differentiation parameter.We discuss first the bound state conditions, and then the continuity conditions.Then,we derive the quantization scheme and we obtain the wave function solution.In Sec.3, we employ the Newton Raphson (NR)method to obtain numerical results out of the derived transcendental equations.We discuss the role of the differentiation parameter on the energy spectrum of GWSP wells with repulsive and attractive surface interactions, respectively.In Sec.4, we give a brief conclusion to finalize the paper.
2 The Klein-Gordon equation and Bound State Solution
We start with the KGE in the SS limit[25]

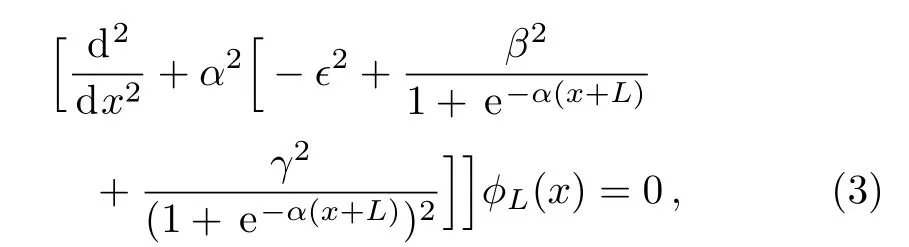
for thex<0 region with the given abbreviations
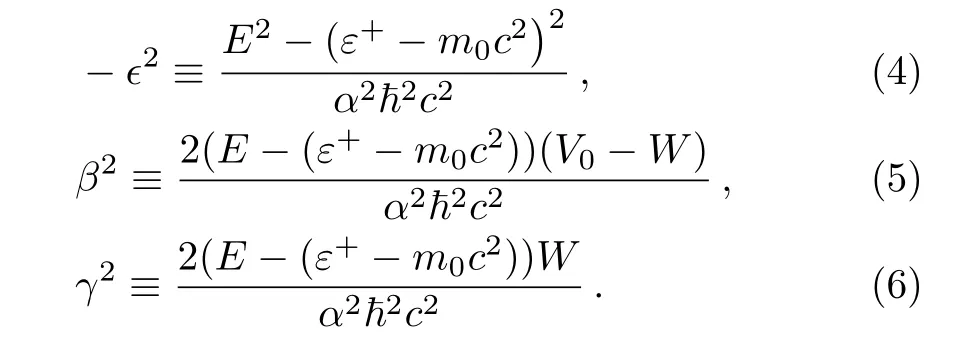
Even though,here we closely follow our previous paper,[25]there is a remarkable difference.We keep the differentiation parameter in the equations in order to investigate its role on the spectrum.By defining a new transformation

we derive a dimensionless equation from Eq.(3)
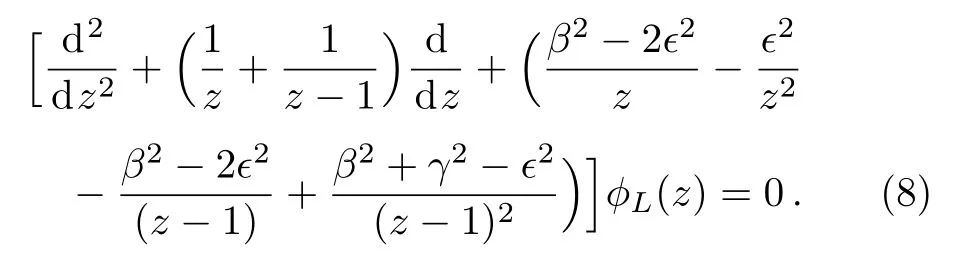
As an ansatz, we propose the general solution in the form of
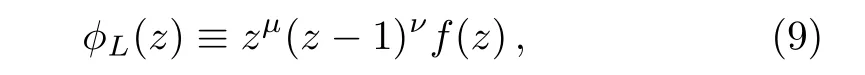
where,µ2−ϵ2=0 andν2+β2+γ2−ϵ2=0.Furthermore,we define positive wave numberskandκ
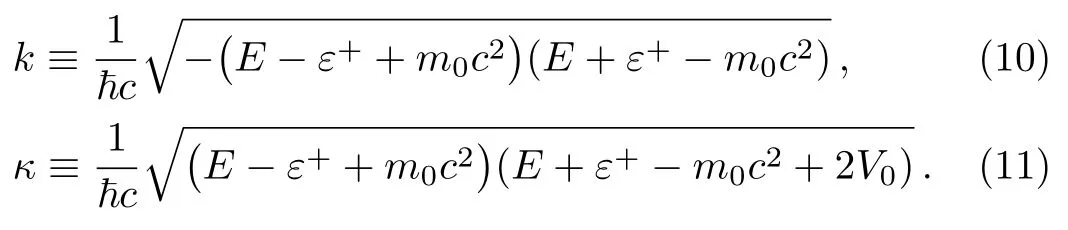
that satisfy

The resulting equation is the Hypergeometric differential equation
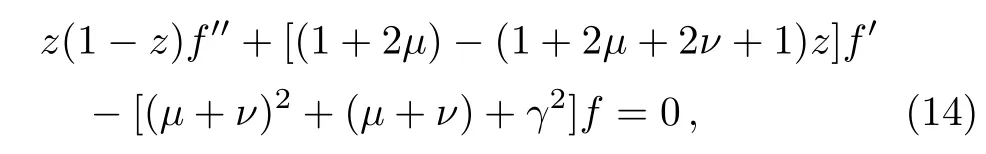
that possesses solutions in terms of2F1, which is a hypergeometric function.Finally,we derive the general solution inx<0 region in the following form
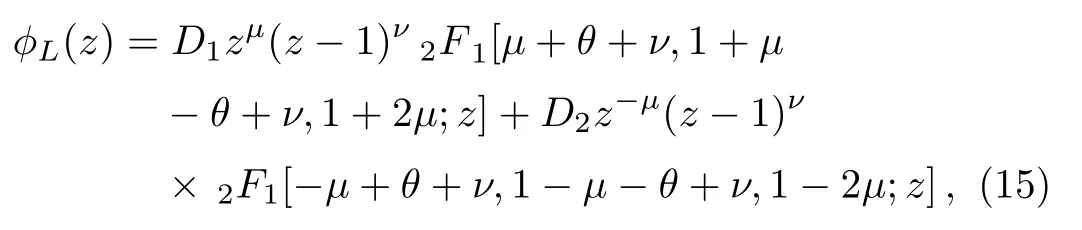
whereθis defined to be
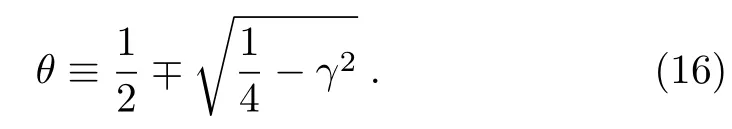
Note that, from now on, we prefer to use the “minus definition” in our calculation.As a consequence of the symmetry,x→−x, of the GSWSP energy, we obtain a symmetric solution in regionx>0.
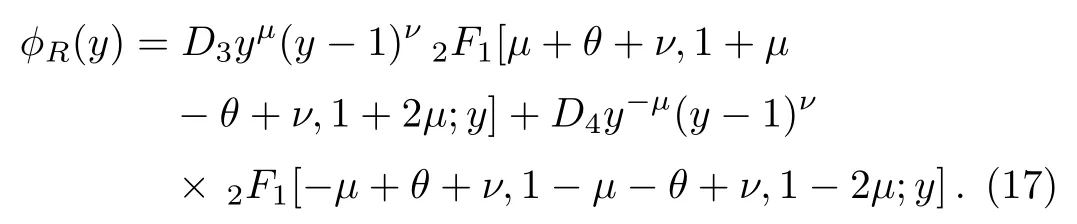
Note that,in the positive region we use the transformation
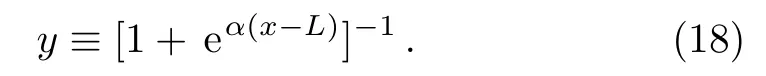
As a final remark, we denote the normalization constants withD1,...,D4.
2.1 Bound State Conditions
In a bound state problem,the boundary condition predicts that the particle’s wave function has to vanish exponentially outside the well.This condition is satisfied if and only if,µis a real number, whereas,νis an imaginary number.We assign these constraints on the wave numbers defined in Eqs.(10)and (11).Then, we obtain the conditions
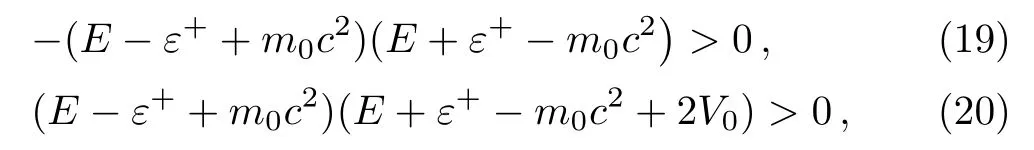
besides to the conditionVcr > V0>0.Here,Vcrvalue is an upper limit of the potential depth parameter due to the Klein paradox.[50]
We investigate these conditions comprehensively in order to comprehend the crucial role of the differentiation parameter.In Fig.1, we display them by representing the parametersV0andEon the axes.The shaded area indicates the intersection of the required constraints.
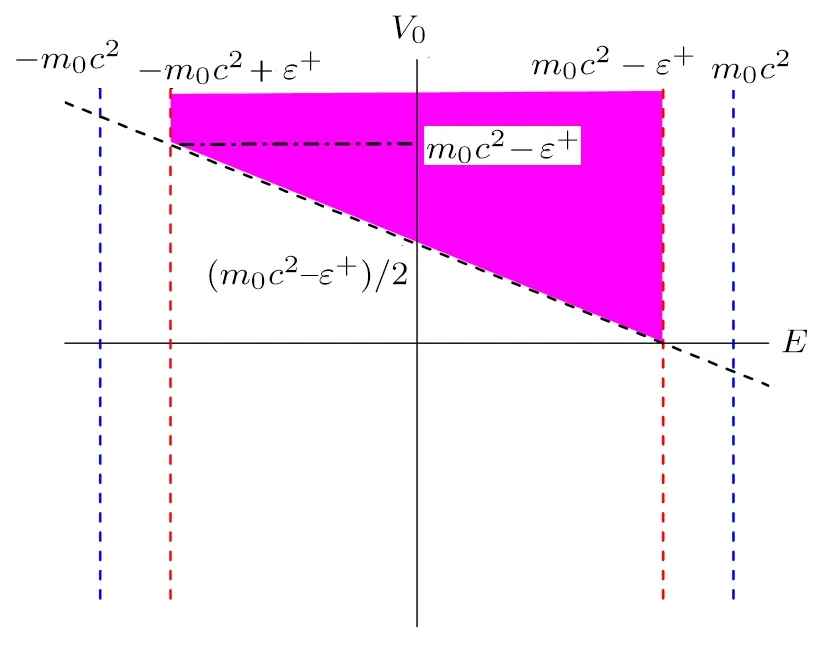
Fig.1 Possible energy eigenvalue region for a confined particle in SS limit.Potential well depth parameter plays a crucial role in order to have positive and/or negative eigenvalues.
We observe that the first constraint, given in Eq.(19),circumscribes the energy spectrum in a limited interval.
The second constraint, given in Eq.(20)determines the possible minimum value limit of the energy spectrum.For instance, the possibility of the occurrence of an energy spectrum that has values only greater than zero depends on the potential depth parameter to be less than(m0c2−ε+)/2.If the potential depth parameter has a value in the interval of (0,m0c2−ε+), then negative values can be obtained in the energy spectrum with constriction.The minimum value limit of the spectrum depends on the value of the depth parameter.Off the greater values of the depth parameter, until a critical value, the energy spectrum occurs with the all the possible values that are allowed from the first constraint given in Eq.(19).Therefore,we conclude that one of the role of the differentiation parameter is to modify the mass energy of the confined particle and consequently to narrow the spectrum interval.
Before we apply the continuity conditions,we examine the behavior of wave functions at positive and negative infinities.We find
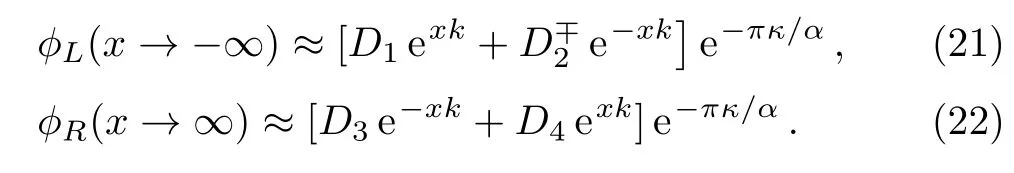
We assume that the name numberskandκare positive numbers.This assumption causes two of the normalization constants,D2andD4, to be equal to zero.
2.2 The Continuity Conditions
If the potential energy has finite values, the continuity condition of the derivative of the wave function is accompanied by the condition of the continuity of the wave function.Therefore, in this study at the critical pointx= 0,the wave function and its derivative should be equal to each other in the positive and negative regions.
After simple and straightforward calculations we obtain two equations that correspond to the continuity of the wave function
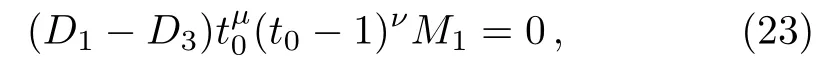
and to the continuity of the derivative of the wave function
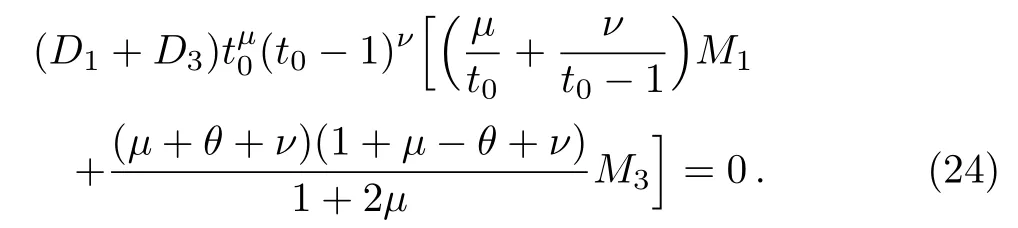
Here, we define
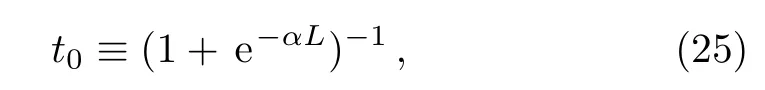
and use new abbreviations
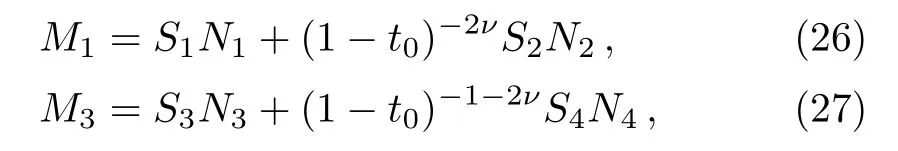
where
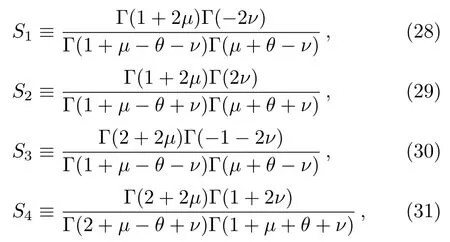
and
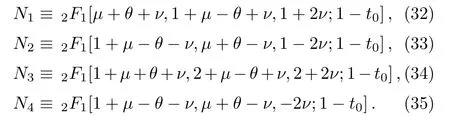
2.3 Quantization and the Wave Function Solutions
We use the continuity conditions, derived in Eqs.(23)and (24), to obtain the energy spectrum.In one dimension, due to the current symmetry, we divide the energy spectrum into two subsets in means of odd and even node numbers.
We obtain the even subset of the energy spectrum,Een,by settingD1=D3.Equation (23)becomes identically equal to zero.The other equation, Eq.(24)yields to
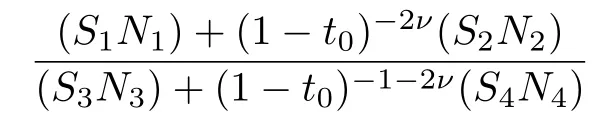
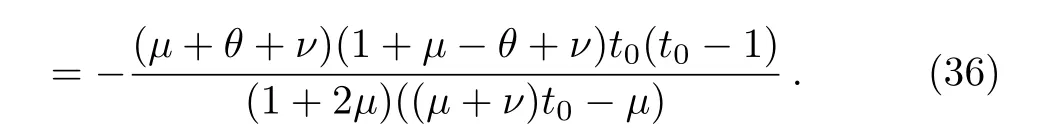
Furthermore, we obtain the even wave function in two parts that corresponds to the negative and positive regions, as follows:

On the other hand, we establish the odd subset of the energy spectrum,Ee0, by settingD1=−D3, hence Eq.(24)becomes to be equal to zero.Moreover, Eq.(23)gives
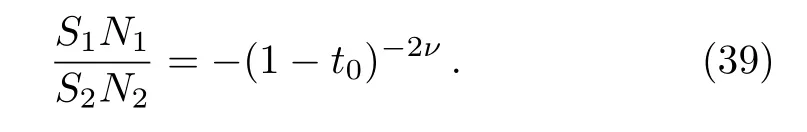
Alike the even case, we obtain the odd wave function in two parts that corresponds to negative and positive regions, respectively.

3 Results and Discussions
In this section we employ the NR numerical methods.We assume that the confined particle in the GSWSP energy well is a neutral Kaon.Note that its rest mass energy ism0c2=497.648 MeV.We suppose that the energy well is constructed withV0=m0c2/2,α= 1 fm−1andL= 6 fm parameters in addition to theW= 2m0c2andW=−2m0c2parameters in the repulsive and attractive surface effects cases, respectively.
3.1 The Role on the Bound State Solutions with Repulsive Surface Effects
To calculate the energy spectra at various values of differentiation parameter, we use the equations obtained in Eqs.(36)and (39).We tabulate the calculated energy spectra in Table 1 with their corresponding node numbers,n.For the various differentiation parameters, we calculate the ratio of the calculated energy spectra to the bound particles’rest mass energy,and then,we plot these ratios with the number of nodes in Fig.2.
In Fig.3, we examine the role of the differentiation parameter on the energy spectrum.The first bound state conditions,given in Eq.(19),states that the Klein-Gordon interval should be in between the pointsAandI.The second condition, given with Eq.(20), constricts the interval to be among the pointsFandI.This analysis is in a complete agreement with the calculated energy spectrum,that possesses only positive values, as given in the second column of Table 1.Note that the allowed interval length is equal tom0c2.
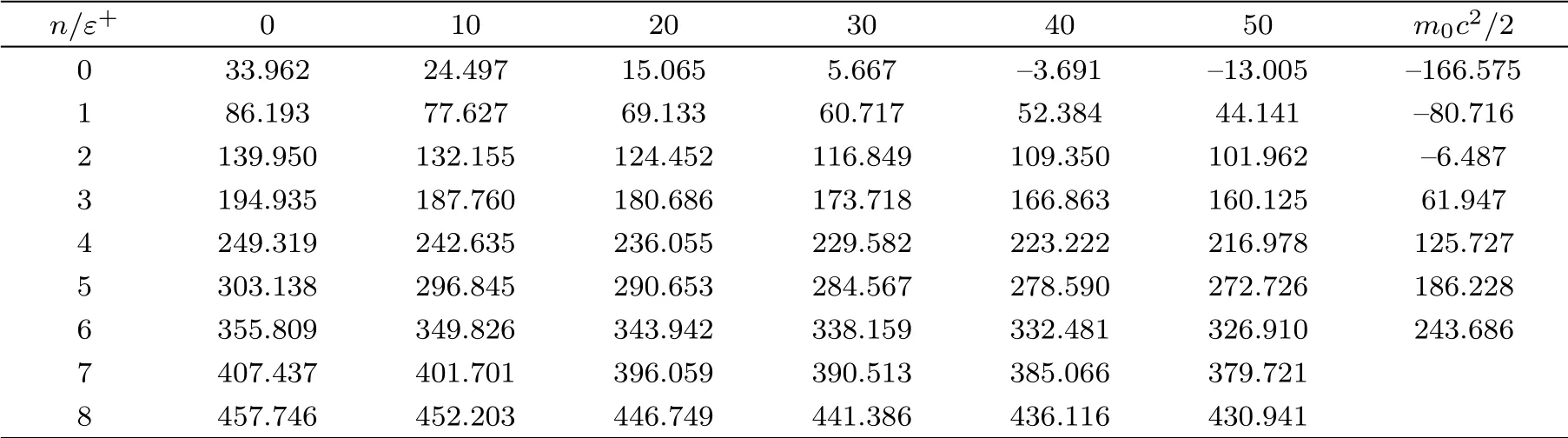
Table 1 Energy spectra for different values of the differentiation parameter for the repulsive surface interaction case.Note that all calculated eigenvalues and ε+ have units in MeV.
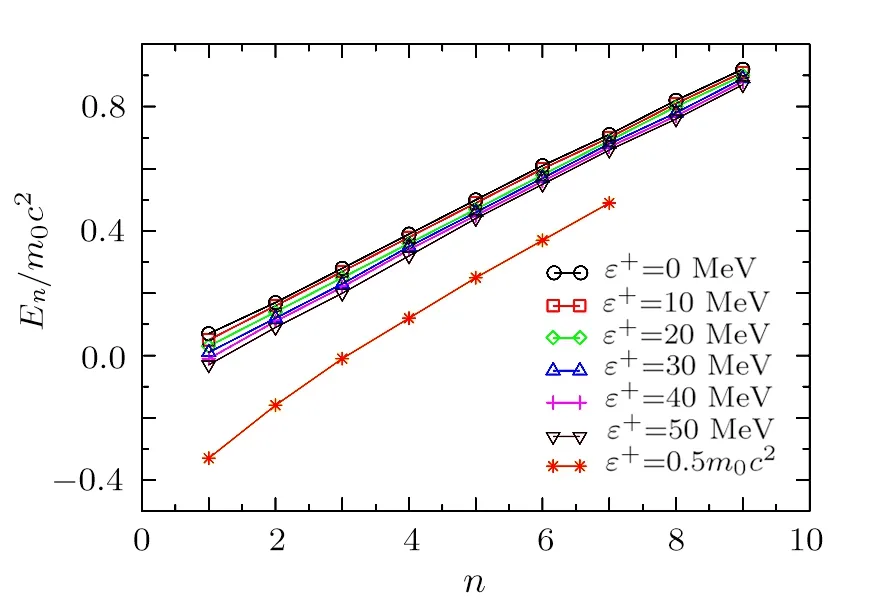
Fig.2 Node numbers versus the rate of the bound state’s energy spectra to the rest mass energy of Kaon particle for different values of ε+ in the existence of the repulsive surface effects.Note that 0.5m0c2=248.824 MeV.

Fig.3 The change of bound state energy spectrum interval for a fixed value of potential depth parameter versus ε+= 0.When ε+= 0, the energy spectrum is constituted with the values of energy between F to I points.While the ε+= 0 increases the Klein-Gordon energy interval shifts to be D to H.Note that the spectrum interval gains a symmetry when ε+ takes the half value of the neutral Kaon mass energy.
In the case of bound state problems, the depth parameter of the potential energy well in which the bound particle is located is initially determined and is constant throughout the problem.The increase of the differentiation parameter plays the role of the shift of the energy interval, due to the conditions that are given in Eq.(20).We demonstrate this effect in Fig.3.For instance, whenε+=50 MeV,FandIpoints shift to the pointsDandH,respectively.The consequence of such a shift the energy spectrum could have negative eigenvalues.In this particular problem, we observe that with the increase of the exchange parameters, the ground state energy eigenvalue approaches to zero and possesses a negative value whenε+=40 MeV,as predicted.We would like to remark that the shifted energy interval’s length does not change via the increase of the differentiation parameter.
Next,we assign an extreme value to the differentiation parameter.When the differentiation parameter is equal tom0c2/2, the shifted Klein-Gordon interval becomes symmetric in betweenCandG.Although the interval length remains constant, we obtain a decrease in the number of the calculated eigenvalues in the energy spectrum.Therefore,we conclude that the differentiation parameter has an effect on the eigenvalue density of the energy spectrum.
Finally, in Fig.4 we investigate the role of the differentiation parameter on the energy step size in their energy spectra.Here, we name the difference between any two consecutive eigenvalues as an energy step size.In each value of the differentiation parameter, the energy step size landscape goes uphill until three increments of node number, then a decrease follows with further increment in node number.When the differentiation parameter exceeds tom0c2/2, the energy step size only decreases with node number increment, but this is not illustrated in Fig.4.The increase in the differentiation parameter gives rise to the increase in the energy step size in the constant interval, therefore, the number of available energy eigenvalues tends to decrease after a critical value.A decrease in the number of nodes untilε+=50 MeV is not observed,whereas,for an asymptotic value of the differentiation parameter,chosen asm0c2/2,the number of nodes decreases from nine to seven.As a final remark, we observe that at the very end of the increment in node number scale, versus the differentiation parameter, the landscape almost flattens with very small step sizes.Contrarily, at the beginning of the increment in node number scale, versus the differentiation parameter, the landscape increases at a relatively high rate as we demonstrate in Fig.4.
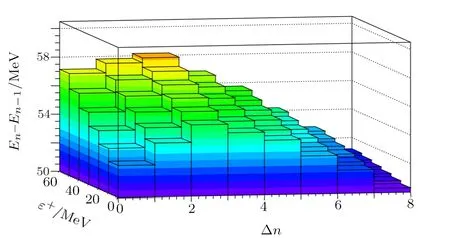
Fig.4 Three-dimensional diagram among the increment of node numbers, the differentiation parameter and energy step size.
3.2 The Role on the Bound State Solutions with Attractive Surface Effects
In this subsection, we employ the NR method to solve Eqs.(36)and (39)forε+= 0 andε+= 50 MeV under the presence of attractive surface effects.In Table 2,we tabulate the calculated energy spectra versus the node numbers.When we chooseε+= 0, we obtain sixteen eigenvalues lowest one’s node number is six.However,when we takeε+= 50 MeV, we find the wave function corresponding to the lowest energy eigenvalue in the spectrum has four node number.In addition,we get seventeen eigenvalues in the energy spectrum.
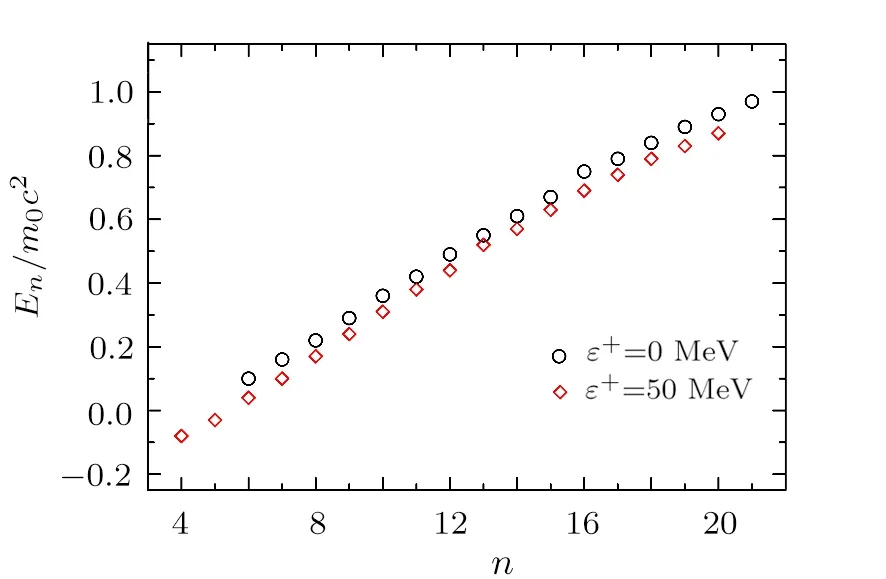
Fig.5 Node numbers versus the rate of the bound state’s energy spectra to the rest mass energy of Kaon particle for different values of the differentiation parameter in the existence of the attractive surface effects.Note that 0.5m0c2=248.824 MeV.
In Fig.5, we plot the node numbers versus the rate of the energy spectra to the rest mass energy of neutral Kaon.We observe that the rate becomes negative with the increase in the parameterε+, similar to the behavior in the repulsive case.On the other hand, the number of energy eigenvalues in the spectrum increase, in contrast with the repulsive case.
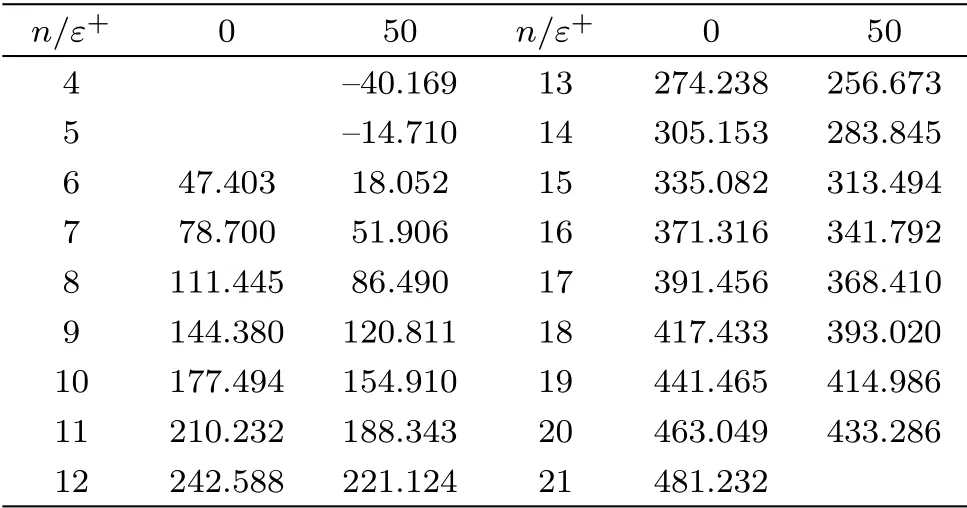
Table 2 Energy spectra for different values of the differentiation parameter for attractive surface forces.Note that all calculated energies and ε+ have units in MeV.
4 Conclusion
In this manuscript,we investigate the role of the differentiation parameter on the solution of the KGE in the SS limit by arising a novel analogy of the variational method.We examine the bound state conditions under the GSWSP energy with the presence of the differentiation parameter.Then, we discuss the continuity condition and quantization scheme.We observe that one of the role of the differentiation parameter is to modify the confined particle’s mass-energy, hence to narrow the spectrum interval length.In order to obtain numerical results,we use a neutral Kaon confinement in a GSWSP energy well.In the presence of differentiation parameters, we obtain various energy spectra for the repulsive and attractive surface effect cases.As consequences of discussions that have been done,we conclude that the differentiation parameter plays the role of to be a measure of the density of the eigenvalues.Furthermore, we show that higher values of differentiation parameter correspond to a greater step size in the spectrum compared to that of its lower values, in both repulsive and attractive surface effects.
Acknowledgments
The author is indebted to Prof.M.Horta¸csu and Prof.for the proof reading.The author thanks to the reviewers for their kind recommendations that lead several improvements in the article.
 Communications in Theoretical Physics2019年3期
Communications in Theoretical Physics2019年3期
- Communications in Theoretical Physics的其它文章
- Entropy Quantization of Schwarzschild Black Hole
- Pull-in Instability Analysis of Nanoelectromechanical Rectangular Plates Including the Intermolecular, Hydrostatic, and Thermal Actuations Using an Analytical Solution Methodology
- Boundary Layer Flow over a Curved Surface Imbedded in Porous Medium
- Spin-Dependent Electron Tunneling in ZnSe/Zn1−xMnxSe Heterostructures with Double δ-Potentials
- Interaction of Wave Trains with Defects∗
- Modulated Dust-Acoustic Wave Packets in an Opposite Polarity Dusty Plasma System
